آشنایی با توابع بازگشتی با پایتون

معرفی

وقتی به تکرار یک کار فکر می کنیم، معمولاً به آن فکر می کنیم for و while حلقه ها این سازه‌ها به ما اجازه می‌دهند که اجرا کنیم تکرار روی یک لیست، مجموعه و غیره

با این حال، شکل دیگری از تکرار یک کار، به روشی کمی متفاوت وجود دارد. با فراخوانی یک تابع در درون خود، برای حل یک نمونه کوچکتر از همان مشکل، در حال انجام هستیم بازگشت.

این توابع تا زمانی که مشکل حل نشود، خود را صدا می زنند، و عملاً مشکل اولیه را به نمونه های کوچکتر زیادی از خود تقسیم می کنند – مثلاً لقمه های کوچکی از یک تکه غذای بزرگتر.

هدف نهایی خوردن کل بشقاب جیب های داغ است، شما این کار را با لقمه زدن بارها و بارها انجام می دهید. هر لقمه یک بازگشتی اقدامی که پس از آن دفعه بعد همان اقدام را انجام می دهید. شما این کار را برای هر لقمه انجام می دهید و ارزیابی می کنید که برای رسیدن به هدف باید یک لقمه دیگر بردارید، تا زمانی که جیب داغی باقی نماند. روی بشقاب شما

بازگشت چیست؟

همانطور که در مقدمه گفته شد، بازگشت شامل الف process خود را در تعریف می نامد. یک تابع بازگشتی به طور کلی دارای دو جزء است:

• را مورد پایه که شرطی است که تعیین می کند تابع بازگشتی چه زمانی باید متوقف شود
• فراخوانی به خودش

بیایید به یک مثال کوچک برای نشان دادن هر دو مؤلفه نگاه کنیم:

def hi_recursive(remaining):
    
    if remaining == 0:
        return
    print('hi')

    
    hi_recursive(remaining - 1)

را مورد پایه برای ما اگر remaining متغیر برابر است با 0 یعنی چند تا باقی مانده است hi رشته ما باید print. تابع به سادگی برمی گردد.

بعد از print بیانیه، ما تماس می گیریم hi_recursive دوباره اما با مقدار باقیمانده کاهش یافته. این مهم است! اگر مقدار آن را کاهش ندهیم remaining تابع به طور نامحدود اجرا خواهد شد. به طور کلی، هنگامی که یک تابع بازگشتی خود را فراخوانی می کند، پارامترها تغییر می کنند تا به حالت پایه نزدیکتر شوند.

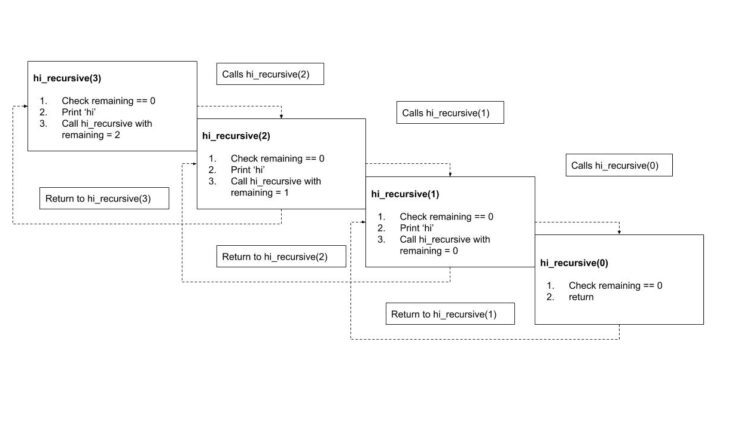
بیایید تجسم کنیم که وقتی تماس می گیریم چگونه کار می کند hi_recursive(3):

پس از چاپ تابع hi، خود را با مقدار کمتری برای فراخوانی می کند remaining تا به آن برسد 0. در صفر، تابع به جایی که فراخوانی شده بود برمی گردد hi_recursive(1)، که به جایی که فراخوانی شده برمی گردد hi_recursive(2) و در نهایت به جایی که فراخوانی شده بود برمی گردد hi_recursive(3).

چرا از حلقه استفاده نمی کنید؟

تمام پیمایش ها را می توان با حلقه ها انجام داد. با این حال، برخی از مشکلات اغلب با بازگشت به جای تکرار آسان‌تر حل می‌شوند. یک مورد رایج برای بازگشت، پیمایش درخت است:

عبور از میان گره‌ها و برگ‌های درخت معمولاً هنگام استفاده از بازگشت آسان‌تر است. حتی اگر حلقه ها و بازگشت هر دو از درخت عبور می کنند، اهداف متفاوتی دارند – حلقه ها برای تکرار یک کار هستند در حالی که بازگشت به معنای تجزیه یک کار بزرگ به وظایف کوچکتر است.

بازگشت با درختان به عنوان مثال به خوبی چنگال چون ما می توانیم process کل درخت با پردازش قسمت های کوچکتر درخت به صورت جداگانه.

مثال ها

بهترین راه برای راحت شدن با بازگشت، یا هر مفهوم برنامه نویسی، تمرین آن است. ایجاد توابع بازگشتی ساده است: حتماً حروف پایه خود را وارد کنید و تابع را طوری فراخوانی کنید که به حروف اصلی نزدیکتر شود.

مجموع یک لیست

پایتون شامل یک sum عملکرد برای لیست ها پیاده سازی پیش فرض پایتون، CPython، از یک حلقه for نامحدود در C برای ایجاد آن توابع استفاده می کند (کد منبع اینجا برای علاقه مندان). بیایید ببینیم چگونه این کار را با بازگشت انجام دهیم:

def sum_recursive(nums):
    if len(nums) == 0:
        return 0

    last_num = nums.pop()
    return last_num + sum_recursive(nums)

مورد پایه لیست خالی است – بهترین sum برای آن است 0. پس از رسیدگی به کیس پایه خود، آخرین مورد از لیست را حذف می کنیم. ما در نهایت به sum_recursive با لیست کاهش یافته عمل کنید و عددی را که خارج کردیم به کل اضافه می کنیم.

در مفسر پایتون sum((10, 5, 2)) و sum_recursive((10, 5, 2)) هر دو باید به شما بدهند 17.

اعداد فاکتوریل

ممکن است به خاطر بیاورید که الف فاکتوریل یک عدد صحیح مثبت، حاصلضرب تمام اعداد صحیح قبل از آن است. مثال زیر آن را واضح تر می کند:

5! = 5 x 4 x 3 x 2 x 1 = 120

علامت تعجب یک فاکتوریل را نشان می دهد و می بینیم که ضرب می کنیم 5 با حاصل ضرب تمام اعداد صحیح از 4 تا 1. اگه کسی وارد بشه چی 0? این به طور گسترده ای درک و اثبات شده است 0! = 1. حالا بیایید یک تابع مانند زیر ایجاد کنیم:

def factorial(n):
    if n == 0 or n == 1:
        return 1
    return n * factorial(n - 1)

ما برای مواردی که 1 یا 0 وارد می شود و در غیر این صورت عدد فعلی را در فاکتوریل عدد کاهش یافته ضرب می کنیم 1.

یک تأیید ساده در مفسر پایتون شما این را نشان می دهد factorial(5) به شما می دهد 120.

دنباله فیبوناچی

آ دنباله فیبوناچی عددی است که در آن هر عدد حاصل جمع دو عدد بعدی است. این دنباله فرض می کند که اعداد فیبوناچی برای 0 و 1 نیز 0 و 1 هستند. بنابراین، معادل فیبوناچی برای 2، 1 خواهد بود.

بیایید دنباله و اعداد طبیعی مربوط به آنها را ببینیم:

    Integers:   0, 1, 2, 3, 4, 5, 6, 7
    Fibonacci:  0, 1, 1, 2, 3, 5, 8, 13

ما می‌توانیم به راحتی تابعی را در پایتون کدنویسی کنیم تا معادل فیبوناچی را برای هر عدد صحیح مثبت با استفاده از بازگشت تعیین کنیم:

def fibonacci(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)

با بررسی آن می توانید تأیید کنید که همانطور که انتظار می رود کار می کند fibonacci(6) برابر است 8.

اکنون می خواهم پیاده سازی دیگری از این تابع را در نظر بگیرید که از یک حلقه for استفاده می کند:

def fibonacci_iterative(n):
    if n <= 1:
        return n

    a = 0
    b = 1
    for i in range(n):
        temp = a
        a = b
        b = b + temp
    return a

اگر عدد صحیح کوچکتر یا مساوی 1 باشد، آن را برگردانید. اکنون که پرونده پایه ما رسیدگی شده است. با ذخیره عدد اول در a به طور پیوسته عدد اول را با عدد دوم جمع می کنیم temp متغیر قبل از اینکه آن را به روز کنیم.

خروجی مشابه اولی است fibonacci() تابع. این نسخه سریعتر از نسخه بازگشتی است، زیرا پیاده سازی های پایتون برای بازگشت بهینه نشده اند، اما با برنامه نویسی ضروری برتری می یابند. با این حال، راه حل به سادگی اولین تلاش ما قابل خواندن نیست. یکی از بزرگترین نقاط قوت بازگشت وجود دارد: ظرافت. برخی از راه حل های برنامه نویسی به طور طبیعی با استفاده از بازگشت حل می شوند.

نتیجه

بازگشت به ما اجازه می دهد تا با فراخوانی مکرر یک کار بزرگ را به وظایف کوچکتر تقسیم کنیم. یک تابع بازگشتی نیاز به یک حالت پایه برای توقف اجرا دارد و به خود فراخوانی نیاز دارد که به تدریج تابع را به حالت پایه هدایت می کند. معمولاً در درختان استفاده می‌شود، اما توابع دیگر را می‌توان با بازگشت به منظور ارائه راه‌حل‌های زیبا نوشت.