ادغام مرتب سازی در پایتون

معرفی

Merge Sort یکی از معروف ترین الگوریتم های مرتب سازی است. اگر در حال تحصیل در رشته کامپیوتر هستید، ادغام مرتب سازی، در کنار Quick Sort احتمالاً اولین الگوریتم مرتب سازی کارآمد و همه منظوره ای است که نام آن را شنیده اید. همچنین یک نمونه کلاسیک از a است تفرقه بینداز و حکومت کن دسته الگوریتم ها

ایده پشت مرتب سازی ادغام

روش ادغام مرتب سازی به این صورت است:

• یک آرایه اولیه به دو قسمت تقریباً مساوی تقسیم می شود. اگر آرایه دارای تعداد فرد عنصر باشد، یکی از آن “نیمه ها” یک عنصر بزرگتر از دیگری است.

• زیرآرایه ها بارها و بارها به دو نیم تقسیم می شوند تا اینکه به آرایه هایی برسید که هر کدام فقط یک عنصر دارند.

• سپس جفت‌های آرایه‌های یک عنصری را در آرایه‌های دو عنصری ترکیب می‌کنید و آنها را در process. سپس این جفت های مرتب شده در آرایه های چهار عنصری ادغام می شوند و به همین ترتیب روی تا زمانی که در نهایت آرایه اولیه مرتب شده باشد.

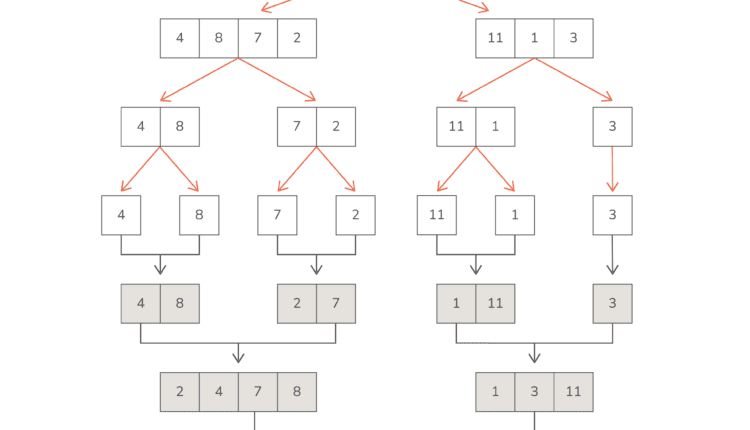
در اینجا یک تجسم از Merge Sort است:

همانطور که می بینید، این واقعیت که آرایه را نمی توان به نیمه های مساوی تقسیم کرد مشکلی نیست، 3 فقط “منتظر” می شود تا مرتب سازی آغاز شود.

دو راه اصلی برای پیاده سازی الگوریتم Merge Sort وجود دارد، یکی استفاده از a بالا پایین رویکرد مانند مثال بالا، که مرتب سازی ادغام اغلب به این صورت است.

رویکرد دیگر، یعنی از پایین به بالا، در جهت مخالف کار می کند، بدون بازگشت (به صورت تکراری کار می کند) – اگر آرایه ما داشته باشد ن عناصری که آن را به آنها تقسیم می کنیم ن زیرآرایه های یک عنصر و مرتب سازی جفت آرایه های یک عنصری مجاور، سپس مرتب سازی جفت های مجاور از آرایه های دو عنصری و غیره روی.

بخش اصلی هر دو این رویکرد این است که چگونه دو آرایه کوچکتر را در یک آرایه بزرگتر ترکیب می کنیم (ادغام می کنیم). این کار کاملاً شهودی انجام می شود، فرض کنید آخرین مرحله را در مثال قبلی خود بررسی می کنیم. ما آرایه ها را داریم:

اولین کاری که انجام می دهیم این است که به عنصر اول هر دو آرایه نگاه کنیم. ما یکی را پیدا می کنیم که کوچکتر است، در مورد ما اینطور است 1، بنابراین اولین عنصر آرایه مرتب شده ما است، و در قسمت جلو حرکت می کنیم ب آرایه:

سپس به جفت عناصر بعدی نگاه می کنیم 2 و 3; 2 کوچکتر است، بنابراین آن را در آرایه مرتب شده خود قرار می دهیم و در آرایه به جلو حرکت می کنیم آ. البته در آرایه جلو نمی رویم ب و ما نشانگر خود را نگه می داریم 3 برای مقایسه های آینده:

با استفاده از همان منطق، در بقیه موارد حرکت می کنیم و در نهایت با آرایه ای از (1, 2, 3, 4, 7, 8, 11).

این دو مورد خاص که ممکن است رخ دهد عبارتند از:

• هر دو زیرآرایه دارای یک عنصر هستند. می‌توانیم در هر یک به جلو حرکت کنیم و عنصر را به آرایه مرتب‌شده اضافه کنیم. از نظر فنی می‌توانیم در هر دو آرایه به جلو حرکت کنیم و هر دو عنصر را به آرایه مرتب‌شده اضافه کنیم، اما زمانی که با عناصر مشابه در هر دو آرایه مواجه می‌شویم، این کار به رفتار خاصی نیاز دارد.
• ما عناصر را در یک زیرآرایه “تمام” می کنیم. به عنوان مثال، یک آرایه با {1، 2، 3} و یک آرایه با {9، 10، 11} داریم. واضح است که ما تمام عناصر آرایه اول را بدون حرکت به جلو حتی یک بار در آرایه دوم مرور خواهیم کرد. هر زمان که در یک زیرآرایه از عناصر کم کنیم، به سادگی عناصر دوم را یکی پس از دیگری اضافه می کنیم.

روش پیاده سازی Merge Sort در پایتون

مرتب سازی ادغام را اجرا خواهیم کرد روی دو نوع مجموعه – روی آرایه های اعداد صحیح (معمولاً برای معرفی مرتب سازی استفاده می شود) و روی اشیاء سفارشی (سناریوی عملی تر و واقعی تر).

ما الگوریتم Merge Sort را با استفاده از بالا پایین رویکرد. الگوریتم خیلی “زیبا” به نظر نمی رسد و می تواند گیج کننده باشد، بنابراین ما هر مرحله را با جزئیات مرور خواهیم کرد.

مرتب سازی آرایه ها

بیایید با بخش آسان شروع کنیم. ایده اصلی الگوریتم این است که آرایه های (زیر) را به دو نیم تقسیم کرده و آنها را به صورت بازگشتی مرتب کنیم. ما می‌خواهیم این کار را تا حد امکان ادامه دهیم، یعنی تا زمانی که به زیرآرایه‌هایی برسیم که فقط یک عنصر دارند:

def merge_sort(array, left_index, right_index):
    if left_index >= right_index:
        return

    middle = (left_index + right_index)//2
    merge_sort(array, left_index, middle)
    merge_sort(array, middle + 1, right_index)
    merge(array, left_index, right_index, middle)

با تماس با merge روش آخر، ما مطمئن می شویم که قبل از شروع مرتب سازی، تمام تقسیمات اتفاق می افتد. ما استفاده می کنیم // عملگر به صراحت در مورد این واقعیت است که ما مقادیر صحیح برای شاخص های خود می خواهیم.

مرحله بعدی بخش ادغام واقعی از طریق چند مرحله و سناریو است:

• از آرایه های ما کپی ایجاد کنید. اولین آرایه زیرآرایه از است (left_index,..,middle) و دومی از (middle+1,...,right_index)
• ما از هر دو نسخه عبور می کنیم (ردیابی نشانگرها در هر دو آرایه)، از بین دو عنصری که در حال حاضر به آنها نگاه می کنیم، کوچکتر را انتخاب می کنیم و آنها را به آرایه مرتب شده خود اضافه می کنیم. در هر آرایه ای که عنصر را انتخاب کرده ایم به جلو حرکت می کنیم و بدون توجه به آرایه مرتب شده به جلو می رویم.
• اگر در یکی از کپی‌هایمان عناصر ما تمام شد – به سادگی عناصر باقی‌مانده در کپی دیگر را به آرایه مرتب شده اضافه کنید.

با توجه به الزامات ما، بیایید جلو برویم و a را تعریف کنیم merge() تابع:

def merge(array, left_index, right_index, middle):
    

    
    left_copy = array(left_index:middle + 1)
    right_copy = array(middle+1:right_index+1)

    
    
    left_copy_index = 0
    right_copy_index = 0
    sorted_index = left_index

    
    while left_copy_index < len(left_copy) and right_copy_index < len(right_copy):

        
        
        if left_copy(left_copy_index) <= right_copy(right_copy_index):
            array(sorted_index) = left_copy(left_copy_index)
            left_copy_index = left_copy_index + 1
        
        else:
            array(sorted_index) = right_copy(right_copy_index)
            right_copy_index = right_copy_index + 1

        
        
        sorted_index = sorted_index + 1

    
    
    while left_copy_index < len(left_copy):
        array(sorted_index) = left_copy(left_copy_index)
        left_copy_index = left_copy_index + 1
        sorted_index = sorted_index + 1

    while right_copy_index < len(right_copy):
        array(sorted_index) = right_copy(right_copy_index)
        right_copy_index = right_copy_index + 1
        sorted_index = sorted_index + 1

حالا بیایید برنامه خود را آزمایش کنیم:

array = (33, 42, 9, 37, 8, 47, 5, 29, 49, 31, 4, 48, 16, 22, 26)
merge_sort(array, 0, len(array) -1)
print(array)

خروجی این است:

(4, 5, 8, 9, 16, 22, 26, 29, 31, 33, 37, 42, 47, 48, 49)

مرتب سازی اشیاء سفارشی

اکنون که الگوریتم اصلی را در اختیار داریم، می‌توانیم نگاهی به روش مرتب‌سازی کلاس‌های سفارشی بیندازیم. ما می توانیم نادیده بگیریم __eq__، __le__، __ge__و سایر اپراتورها در صورت نیاز برای این کار.

این به ما امکان می دهد از همان الگوریتم فوق استفاده کنیم، اما ما را به تنها یک راه برای مرتب سازی اشیاء سفارشی محدود می کند، که در بیشتر موارد آن چیزی نیست که ما می خواهیم. ایده بهتر این است که خود الگوریتم را متنوع تر کنید و به جای آن یک تابع مقایسه را به آن منتقل کنید.

ابتدا یک سفارشی را پیاده سازی می کنیم Car کلاس و چند فیلد به آن اضافه کنید:

class Car:
    def __init__(self, make, model, year):
        self.make = make
        self.model = model
        self.year = year

    def __str__(self):
        return str.format("Make: {}, Model: {}, Year: {}", self.make, self.model, self.year)

سپس چند تغییر در روش‌های مرتب‌سازی ادغام ایجاد می‌کنیم. ساده ترین راه برای رسیدن به آنچه می خواهیم استفاده از توابع لامبدا است. می بینید که ما فقط یک پارامتر اضافی اضافه کردیم و فراخوانی های متد را بر این اساس تغییر دادیم و فقط یک خط کد دیگر را تغییر دادیم تا این الگوریتم بسیار متنوع تر شود:

def merge(array, left_index, right_index, middle, comparison_function):
    left_copy = array(left_index:middle + 1)
    right_copy = array(middle+1:right_index+1)

    left_copy_index = 0
    right_copy_index = 0
    sorted_index = left_index

    while left_copy_index < len(left_copy) and right_copy_index < len(right_copy):

        
        if comparison_function(left_copy(left_copy_index), right_copy(right_copy_index)):
            array(sorted_index) = left_copy(left_copy_index)
            left_copy_index = left_copy_index + 1
        else:
            array(sorted_index) = right_copy(right_copy_index)
            right_copy_index = right_copy_index + 1

        sorted_index = sorted_index + 1

    while left_copy_index < len(left_copy):
        array(sorted_index) = left_copy(left_copy_index)
        left_copy_index = left_copy_index + 1
        sorted_index = sorted_index + 1

    while right_copy_index < len(right_copy):
        array(sorted_index) = right_copy(right_copy_index)
        right_copy_index = right_copy_index + 1
        sorted_index = sorted_index + 1


def merge_sort(array, left_index, right_index, comparison_function):
    if left_index >= right_index:
        return

    middle = (left_index + right_index)//2
    merge_sort(array, left_index, middle, comparison_function)
    merge_sort(array, middle + 1, right_index, comparison_function)
    merge(array, left_index, right_index, middle, comparison_function)

بیایید الگوریتم اصلاح شده خود را آزمایش کنیم روی تعداد کمی Car موارد:

car1 = Car("Alfa Romeo", "33 SportWagon", 1988)
car2 = Car("Chevrolet", "Cruze Hatchback", 2011)
car3 = Car("Corvette", "C6 Couple", 2004)
car4 = Car("Cadillac", "Seville Sedan", 1995)

array = (car1, car2, car3, car4)

merge_sort(array, 0, len(array) -1, lambda carA, carB: carA.year < carB.year)

print("Cars sorted by year:")
for car in array:
    print(car)

print()
merge_sort(array, 0, len(array) -1, lambda carA, carB: carA.make < carB.make)
print("Cars sorted by make:")
for car in array:
    print(car)

خروجی را می گیریم:

Cars sorted by year:
Make: Alfa Romeo, Model: 33 SportWagon, Year: 1988
Make: Cadillac, Model: Seville Sedan, Year: 1995
Make: Corvette, Model: C6 Couple, Year: 2004
Make: Chevrolet, Model: Cruze Hatchback, Year: 2011

Cars sorted by make:
Make: Alfa Romeo, Model: 33 SportWagon, Year: 1988
Make: Cadillac, Model: Seville Sedan, Year: 1995
Make: Chevrolet, Model: Cruze Hatchback, Year: 2011
Make: Corvette, Model: C6 Couple, Year: 2004

بهینه سازی

بیایید به تفصیل توضیح دهیم روی تفاوت میان بالا پایین و از پایین به بالا ادغام مرتب سازی در حال حاضر. از پایین به بالا مانند نیمه دوم کار می کند بالا پایین رویکردی که در آن به جای فراخوانی بازگشتی مرتب سازی روی زیرآرایه های نصف شده، ما به طور مکرر زیرآرایه های مجاور را مرتب می کنیم.

یکی از کارهایی که می توانیم برای بهبود این الگوریتم انجام دهیم این است که به جای عناصر تک، تکه های مرتب شده را در نظر بگیرید قبل از شکستن آرایه

این بدان معنی است که با توجه به آرایه ای مانند (4, 8, 7, 2, 11, 1, 3)، به جای تجزیه آن به (4), (8), (7), (2), (11), (1) ,(3) – به زیرآرایه هایی تقسیم می شود که ممکن است قبلاً مرتب شده باشند: (4,8), (7), (2,11), (1,3)، و سپس آنها را مرتب کنید.

با داده‌های واقعی، ما اغلب تعداد زیادی از این زیرآرایه‌های مرتب شده‌ای داریم که می‌توانند زمان اجرای Merge Sort را به‌طور قابل توجهی کوتاه کنند.

نکته دیگری که باید با Merge Sort در نظر گرفت، به ویژه بالا پایین نسخه است چند رشته ای. مرتب سازی ادغام برای این کار راحت است زیرا هر نیمه می تواند مستقل از جفت خود مرتب شود. تنها چیزی که باید از آن مطمئن شویم این است که مرتب سازی هر نیمه قبل از ادغام آنها تمام شده است.

با این حال مرتب سازی ادغام نسبتاً ناکارآمد است (هم در زمان و هم مکان). آرایه های کوچکتر و اغلب با توقف زمانی که به آرایه ای از 7 عنصر می رسیم، به جای پایین رفتن به آرایه های دارای یک عنصر، و فراخوانی Insertion Sort برای مرتب کردن آنها، قبل از ادغام در یک آرایه بزرگتر، بهینه می شود.

این به این دلیل است که مرتب سازی درج با آرایه های کوچک و/یا تقریبا مرتب شده بسیار خوب کار می کند.

نتیجه

Merge Sort یک الگوریتم مرتب سازی کارآمد و همه منظوره است. مزیت اصلی آن زمان اجرای قابل اعتماد الگوریتم و کارایی آن هنگام مرتب سازی آرایه های بزرگ است. بر خلاف Quick Sort، به آن بستگی ندارد روی هر تصمیم ناخوشایندی که منجر به زمان اجرا بد شود.

یکی از اشکالات اصلی حافظه اضافی است که Merge Sort برای ذخیره کپی های موقت آرایه ها قبل از ادغام آنها استفاده می کند. با این حال، Merge Sort یک مثال عالی و شهودی برای معرفی مهندسان نرم افزار آینده با رویکرد تقسیم و غلبه برای ایجاد الگوریتم است.

ما مرتب سازی ادغام هر دو را پیاده سازی کرده ایم روی آرایه های اعداد صحیح ساده و روی اشیاء سفارشی از طریق تابع لامبدا که برای مقایسه استفاده می شود. در پایان، بهینه‌سازی‌های ممکن برای هر دو رویکرد به اختصار مورد بحث قرار گرفت.