از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
ایجاد یک شبکه عصبی از ابتدا در پایتون: طبقه بندی چند کلاسه
سرفصلهای مطلب
این سومین مقاله از مجموعه مقالات است روی “ایجاد یک شبکه عصبی از ابتدا در پایتون”.
اگر تجربه قبلی با شبکه های عصبی ندارید، پیشنهاد می کنم ابتدا قسمت 1 و قسمت 2 این مجموعه را بخوانید (لینک بالا). هنگامی که با مفاهیم توضیح داده شده در آن مقالات احساس راحتی کردید، می توانید برگردید و این مقاله را ادامه دهید.
معرفی
در مقاله قبلی دیدیم که چگونه می توانیم یک شبکه عصبی از ابتدا ایجاد کنیم که قادر به حل مسائل طبقه بندی باینری در پایتون است. یک مسئله طبقه بندی باینری تنها دو خروجی دارد. با این حال، مشکلات دنیای واقعی بسیار پیچیده تر هستند.
مثالی از مسئله تشخیص رقم را در نظر بگیرید که در آن از تصویر یک رقم به عنوان ورودی استفاده می کنیم و طبقه بندی کننده عدد رقم مربوطه را پیش بینی می کند. یک رقم می تواند هر عددی بین 0 و 9 باشد. این یک مثال کلاسیک از یک مسئله طبقه بندی چند کلاسه است که در آن ورودی ممکن است به هر یک از 10 خروجی ممکن تعلق داشته باشد.
در این مقاله خواهیم دید که چگونه می توانیم یک شبکه عصبی ساده از ابتدا در پایتون ایجاد کنیم که قادر به حل مسائل طبقه بندی چند کلاسه است.
مجموعه داده
بیایید ابتدا نگاهی کوتاه به مجموعه داده خود بیندازیم. مجموعه داده ما دو ویژگی ورودی و یکی از سه خروجی ممکن خواهد داشت. ما به صورت دستی یک مجموعه داده برای این مقاله ایجاد می کنیم.
برای انجام این کار، اسکریپت زیر را اجرا کنید:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
cat_images = np.random.randn(700, 2) + np.array((0, -3))
mouse_images = np.random.randn(700, 2) + np.array((3, 3))
dog_images = np.random.randn(700, 2) + np.array((-3, 3))
در اسکریپت بالا، ما با وارد کردن کتابخانههای خود شروع میکنیم و سپس سه آرایه دو بعدی به اندازه 700 x 2 ایجاد میکنیم. میتوانید هر عنصر را در یک مجموعه از آرایه به عنوان تصویری از یک حیوان خاص در نظر بگیرید. هر عنصر آرایه مربوط به یکی از سه کلاس خروجی است.
نکته مهمی که در اینجا باید به آن توجه کرد این است که اگر عناصر the را رسم کنیم cat_images آرایه روی یک صفحه دو بعدی، آنها در مرکز x=0 و y=-3 خواهند بود. به طور مشابه، عناصر از mouse_images آرایه حول محور x=3 و y=3 و در نهایت عناصر آرایه خواهد بود dog_images حول محور x=-3 و y=3 خواهد بود. هنگامی که مجموعه داده خود را رسم می کنیم، این را خواهید دید.
در مرحله بعد، باید به صورت عمودی به این آرایه ها بپیوندیم تا مجموعه داده نهایی خود را ایجاد کنیم. برای این کار اسکریپت زیر را اجرا کنید:
feature_set = np.vstack((cat_images, mouse_images, dog_images))
ما مجموعه ویژگی های خود را ایجاد کردیم و اکنون باید برچسب های مربوطه را برای هر رکورد در مجموعه ویژگی های خود تعریف کنیم. اسکریپت زیر این کار را انجام می دهد:
labels = np.array((0)*700 + (1)*700 + (2)*700)
اسکریپت فوق یک آرایه تک بعدی از 2100 عنصر ایجاد می کند. 700 عنصر اول به عنوان 0 برچسب گذاری شده اند، 700 عنصر بعدی با عنوان 1 برچسب گذاری شده اند در حالی که 700 عنصر آخر به عنوان 2 برچسب گذاری شده اند. این تنها راه میانبر ما برای ایجاد سریع برچسب ها برای داده های مربوطه است.
برای مسائل طبقه بندی چند کلاسه، ما باید برچسب خروجی را به عنوان یک بردار رمزگذاری شده یک داغ تعریف کنیم زیرا لایه خروجی ما دارای سه گره و هر گره خواهد بود. node با یک کلاس خروجی مطابقت خواهد داشت. ما می خواهیم که زمانی که یک خروجی پیش بینی می شود، مقدار مربوطه باشد node باید 1 باشد در حالی که گره های باقیمانده باید مقدار 0 داشته باشند. برای آن، برای هر رکورد به سه مقدار برای برچسب خروجی نیاز داریم. به همین دلیل است که ما بردار خروجی خود را به یک بردار کدگذاری شده یک داغ تبدیل می کنیم.
اسکریپت زیر را برای ایجاد آرایه برداری رمزگذاری شده یک داغ برای مجموعه داده ما اجرا کنید:
one_hot_labels = np.zeros((2100, 3))
for i in range(2100):
one_hot_labels(i, labels(i)) = 1
در اسکریپت بالا ما ایجاد می کنیم one_hot_labels آرایه ای به اندازه 2100 x 3 که در آن هر ردیف حاوی یک بردار رمزگذاری شده یک داغ برای رکورد مربوطه در مجموعه ویژگی است. سپس 1 را در ستون مربوطه درج می کنیم.
اگر اسکریپت بالا را اجرا کنید، خواهید دید که one_hot_labels آرایه 1 در شاخص 0 برای 700 رکورد اول، 1 در شاخص 1 برای 700 رکورد بعدی و 1 در شاخص 2 برای 700 رکورد آخر خواهد داشت.
اکنون بیایید مجموعه داده ای را که به تازگی ایجاد کرده ایم رسم کنیم. اسکریپت زیر را اجرا کنید:
plt.scatter(feature_set(:,0), feature_set(:,1), c=labels, cmap='plasma', s=100, alpha=0.5)
plt.show()
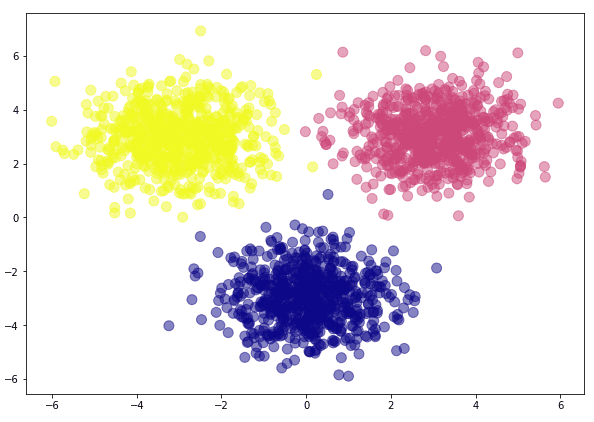
پس از اجرای اسکریپت بالا، باید شکل زیر را مشاهده کنید:

شما به وضوح می بینید که ما عناصر متعلق به سه کلاس مختلف را داریم. وظیفه ما ایجاد یک شبکه عصبی با قابلیت طبقه بندی داده ها در کلاس های فوق خواهد بود.
شبکه عصبی با کلاس های خروجی چندگانه
شبکه عصبی که قصد طراحی آن را داریم دارای معماری زیر است:

میتوانید ببینید که شبکه عصبی ما تقریباً شبیه به شبکهای است که در قسمت 2 مجموعه توسعه دادیم. دارای یک لایه ورودی با 2 ویژگی ورودی و یک لایه پنهان با 4 گره است. با این حال، در لایه خروجی، می بینیم که سه گره داریم. این بدان معنی است که شبکه عصبی ما قادر به حل مسئله طبقه بندی چند کلاسه است که در آن تعداد خروجی های ممکن 3 است.
توابع Softmax و Cross-Entropy
قبل از اینکه حرکت کنیم روی به بخش کد، اجازه دهید به طور خلاصه به بررسی آن بپردازیم سافت مکس و آنتروپی متقابل توابع، که به ترتیب رایج ترین توابع فعال سازی و از دست دادن برای ایجاد یک شبکه عصبی برای طبقه بندی چند کلاسه هستند.
عملکرد سافت مکس
از معماری شبکه عصبی ما، میتوان دریافت که سه گره در لایه خروجی داریم. ما چندین گزینه برای عملکرد فعال سازی در لایه خروجی داریم. یکی از گزینه ها استفاده از تابع sigmoid است که در مقاله های قبلی انجام دادیم.
با این حال، یک تابع فعالسازی راحتتر به شکل softmax وجود دارد که یک بردار را به عنوان ورودی میگیرد و بردار دیگری با همان طول خروجی تولید میکند. از آنجایی که خروجی ما شامل سه گره است، می توانیم خروجی هر کدام را در نظر بگیریم node به عنوان یکی از عناصر بردار ورودی. خروجی طولی از همان بردار خواهد بود که مجموع مقادیر همه عناصر برابر با 1 است. از نظر ریاضی، تابع softmax می تواند به صورت زیر نمایش داده شود:
$$ y_i(z_i) = \frac{e^{z_i}}{ \sum\nlimits_{k=1}^{k}{e^{z_k}} } $$
تابع softmax به سادگی توان هر عنصر ورودی را بر مجموع نماهای همه عناصر ورودی تقسیم می کند. بیایید به یک مثال ساده از این نگاه کنیم:
def softmax(A):
expA = np.exp(A)
return expA / expA.sum()
nums = np.array((4, 5, 6))
print(softmax(nums))
در اسکریپت بالا ما یک تابع softmax ایجاد میکنیم که یک بردار را به عنوان ورودی میگیرد، نماهای تمام عناصر بردار را میگیرد و سپس اعداد حاصل را به صورت جداگانه بر مجموع توانهای همه اعداد در بردار ورودی تقسیم میکند.
می بینید که بردار ورودی شامل عناصر 4، 5 و 6 است. در خروجی، سه عدد را خواهید دید که بین 0 و 1 له شده اند که مجموع اعداد برابر با 1 خواهد بود. خروجی به این صورت است:
(0.09003057 0.24472847 0.66524096)
تابع فعال سازی سافت مکس دو مزیت عمده نسبت به سایر توابع فعال سازی دارد، به خصوص برای مسائل طبقه بندی چند کلاسه: مزیت اول این است که تابع سافت مکس یک بردار را به عنوان ورودی می گیرد و مزیت دوم این است که خروجی بین 0 و 1 تولید می کند. در مجموعه داده ما، برچسبهای خروجی کدگذاری شده یکطرفه داریم که به این معنی است که خروجی ما مقادیری بین 0 و 1 خواهد داشت. با این حال، خروجی فید فوروارد process می تواند بزرگتر از 1 باشد، بنابراین تابع softmax انتخاب ایده آلی در لایه خروجی است زیرا خروجی را بین 0 و 1 له می کند.
تابع متقابل آنتروپی
با عملکرد فعال سازی softmax در لایه خروجی، خطای میانگین مربعات همانطور که در مقاله های قبلی انجام دادیم می توان از تابع cost برای بهینه سازی هزینه استفاده کرد. با این حال، برای تابع softmax، یک تابع هزینه راحتتر وجود دارد که آنتروپی متقاطع نامیده میشود.
از نظر ریاضی، تابع آنتروپی متقابل به شکل زیر است:
$$ H(y,\hat{y}) = -\sum_i y_i \log \hat{y_i} $$
آنتروپی متقاطع به سادگی مجموع حاصل از همه احتمالات واقعی با ورود به سیستم منفی احتمالات پیش بینی شده است. برای مسائل طبقه بندی چند طبقه، تابع آنتروپی متقاطع شناخته شده است که عملکرد بهتری از تابع نزول گرادیان دارد.
اکنون ما دانش کافی برای ایجاد یک شبکه عصبی داریم که مسائل طبقه بندی چند کلاسه را حل می کند. بیایید ببینیم شبکه عصبی ما چگونه کار خواهد کرد.
مثل همیشه، یک شبکه عصبی در دو مرحله اجرا میشود: پیشخور و انتشار پس.
فید فوروارد
فاز فید فوروارد کمابیش مشابه آنچه در مقاله قبلی دیدیم باقی خواهد ماند. تنها تفاوت این است که اکنون ما از تابع فعال سازی softmax در لایه خروجی به جای تابع sigmoid استفاده خواهیم کرد.
به یاد داشته باشید، برای خروجی لایه پنهان همچنان از تابع sigmoid مانند قبل استفاده خواهیم کرد. تابع softmax فقط برای فعال سازی لایه خروجی استفاده خواهد شد.
فاز 1
از آنجایی که ما از دو تابع فعال سازی مختلف برای لایه پنهان و لایه خروجی استفاده می کنیم، فاز پیشخور را به دو فاز فرعی تقسیم کردم.
در مرحله اول روش محاسبه خروجی از لایه پنهان را خواهیم دید. برای هر رکورد ورودی، دو ویژگی “x1” و “x2” داریم. برای محاسبه مقادیر خروجی برای هر کدام node در لایه پنهان، باید ورودی را با وزن های مربوط به لایه پنهان ضرب کنیم. node که برای آن مقدار را محاسبه می کنیم. توجه داشته باشید، ما در اینجا یک اصطلاح تعصب اضافه می کنیم. سپس محصول نقطهای را از تابع فعالسازی سیگموئید عبور میدهیم تا مقدار نهایی را بدست آوریم.
به عنوان مثال برای محاسبه مقدار نهایی برای اولین node در لایه پنهان که با “ah1” مشخص می شود، باید محاسبه زیر را انجام دهید:
$$
zh1 = x1w1 + x2w2 + b
$$
$$
ah1 = \frac{\mathrm{1} }{\mathrm{1} + e^{-zh1} }
$$
این مقدار به دست آمده برای بالاترین بیشترین است node در لایه پنهان به همین ترتیب، می توانید مقادیر گره های 2، 3 و 4 لایه پنهان را محاسبه کنید.
فاز 2
برای محاسبه مقادیر لایه خروجی، مقادیر موجود در گره های لایه پنهان به عنوان ورودی در نظر گرفته می شوند. بنابراین، برای محاسبه خروجی، مقادیر گره های لایه پنهان را با وزن متناظر آنها ضرب کنید و نتیجه را از یک تابع فعال سازی عبور دهید که در این حالت softmax خواهد بود.
این عملیات را می توان به صورت ریاضی با معادله زیر بیان کرد:
$$
zo1 = ah1w9 + ah2w10 + ah3w11 + ah4w12
$$
$$
zo2 = ah1w13 + ah2w14 + ah3w15 + ah4w16
$$
$$
zo3 = ah1w17 + ah2w18 + ah3w19 + ah4w20
$$
در اینجا zo1، zo2 و zo3 بردار را تشکیل می دهند که به عنوان ورودی تابع سیگموئید استفاده می کنیم. بیایید نام این بردار را “زو” بگذاریم.
zo = (zo1, zo2, zo3)
حال برای یافتن مقدار خروجی a01 می توانیم از تابع softmax به صورت زیر استفاده کنیم:
$$
ao1(zo) = \frac{e^{zo1}}{ \sum\nlimits_{k=1}^{k}{e^{zok}} }
$$
در اینجا “a01” خروجی برای بالاترین ها است node در لایه خروجی به همین ترتیب می توانید از تابع softmax برای محاسبه مقادیر ao2 و ao3 استفاده کنید.
میتوانید ببینید که گام پیشخور برای یک شبکه عصبی با خروجی چند کلاسه تقریباً شبیه به مرحله پیشخور شبکه عصبی برای مسائل طبقهبندی باینری است. تنها تفاوت این است که در اینجا ما از تابع softmax در لایه خروجی به جای تابع sigmoid استفاده می کنیم.
پس انتشار
ایده اصلی در پس انتشار مجدد یکسان است. ما باید تابع هزینه را تعریف کنیم و سپس آن تابع هزینه را با به روز رسانی وزن ها به گونه ای بهینه کنیم که هزینه به حداقل برسد. با این حال، بر خلاف مقالات قبلی که در آن استفاده کردیم خطای میانگین مربعات به عنوان یک تابع هزینه، در این مقاله به جای آن از تابع آنتروپی متقابل استفاده خواهیم کرد.
پس انتشار یک است مشکل بهینه سازی جایی که باید پیدا کنیم حداقل عملکرد برای تابع هزینه ما
برای یافتن مینیمم یک تابع، می توانیم از عبارت استفاده کنیم شیب مناسب الگوریتم الگوریتم نزول گرادیان را می توان به صورت ریاضی به صورت زیر نشان داد:
$$ تکرار \ تا \ همگرایی: \begin{Bmatrix} w_j := w_j – \alpha \frac{\partial }{\partial w_j} J(w_0,w_1 ……. w_n) \end{Bmatrix} …………. (1) $$
جزئیات در مورد اینکه چگونه تابع نزولی گرادیان هزینه را به حداقل می رساند قبلاً در مقاله قبلی مورد بحث قرار گرفته است. در اینجا ما فقط عملیات ریاضی را می بینیم که باید انجام دهیم.
تابع هزینه ما این است:
$$ H(y,\hat{y}) = -\sum_i y_i \log \hat{y_i} $$
در شبکه عصبی ما یک بردار خروجی داریم که در آن هر عنصر بردار با خروجی یکی مطابقت دارد node در لایه خروجی بردار خروجی با استفاده از تابع softmax محاسبه می شود. اگر “ao” بردار خروجی های پیش بینی شده از تمام گره های خروجی و “y” بردار خروجی های واقعی گره های مربوطه در بردار خروجی باشد، اساساً باید این تابع را به حداقل برسانیم:
$$ هزینه(y, {ao}) = -\sum_i y_i \log {ao_i} $$
فاز 1
در مرحله اول باید وزن های w9 تا w20 را به روز کنیم. اینها وزن گره های لایه خروجی هستند.
از مقاله قبل، می دانیم که برای به حداقل رساندن تابع هزینه، باید مقادیر وزن را طوری به روز کنیم که هزینه کاهش یابد. برای انجام این کار، باید مشتق تابع هزینه را با توجه به هر وزن در نظر بگیریم. از نظر ریاضی می توانیم آن را به صورت زیر نمایش دهیم:
$$
\frac {dcost}{dwo} = \frac {dcost}{dao} *, \frac {dao}{dzo} * \frac {dzo}{dwo} ….. (1)
$$
در اینجا “wo” به وزن های موجود در لایه خروجی اشاره دارد.
بخش اول معادله را می توان به صورت زیر نشان داد:
$$
\frac {dcost}{dao} *\ \frac {dao}{dzo} …… (2)
$$
مشتق دقیق تابع از دست دادن آنتروپی متقاطع با تابع فعال سازی softmax را می توان در اینجا یافت این لینک.
مشتق معادله (2) عبارت است از:
$$
\frac {dcost}{dao} *\ \frac {dao}{dzo} = ao – y ……. (3)
$$
جایی که “ao” خروجی پیش بینی شده است در حالی که “y” خروجی واقعی است.
در نهایت، ما باید “dzo” را با توجه به “dwo” از پیدا کنیم معادله 1. مشتق به سادگی خروجی هایی است که از لایه پنهان می آیند، همانطور که در زیر نشان داده شده است:
$$
\frac {dzo}{dwo} = آه
$$
برای یافتن مقادیر وزن جدید، مقادیر توسط معادله 1 را می توان به سادگی با نرخ یادگیری ضرب کرد و از مقادیر وزن فعلی کم کرد.
همچنین باید بایاس “bo” را برای لایه خروجی به روز کنیم. ما باید تابع هزینه خود را با توجه به سوگیری متمایز کنیم تا ارزش سوگیری جدید را همانطور که در زیر نشان داده شده است بدست آوریم:
$$
\frac {dcost}{dbo} = \frac {dcost}{dao} *\ \frac {dao}{dzo} * \frac {dzo}{dbo} ….. (4)
$$
قسمت اول از معادله 4 قبلا در محاسبه شده است معادله 3. در اینجا فقط باید “dzo” را با توجه به “bo” که به سادگی 1 است به روز کنیم. بنابراین:
$$
\frac {dcost}{dbo} = ao – y ……….. (5)
$$
برای یافتن مقادیر بایاس جدید برای لایه خروجی، مقادیر توسط معادله 5 را می توان به سادگی با نرخ یادگیری ضرب کرد و از مقدار تعصب فعلی کم کرد.
فاز 2
در این بخش، خطای خود را به لایه قبلی باز میگردانیم و مقادیر وزن جدید را برای وزنهای لایه پنهان یعنی وزنهای w1 تا w8 پیدا میکنیم.
بیایید مجموعاً وزن لایه های پنهان را به عنوان “wh” نشان دهیم. ما اساساً باید تابع هزینه را با توجه به “wh” متمایز کنیم.
از نظر ریاضی می توانیم از قانون زنجیره تمایز برای نمایش آن به صورت زیر استفاده کنیم:
$$
\frac {dcost}{dwh} = \frac {dcost}{dah} *, \frac {dah}{dzh} * \frac {dzh}{dwh} …… (6)
$$
اینجا باز هم میشکنیم معادله 6 به شرایط فردی
اولین عبارت “dcost” را می توان با توجه به “dah” با استفاده از قانون زنجیره ای تمایز به صورت زیر متمایز کرد:
$$
\frac {dcost}{dah} = \frac {dcost}{dzo} *\ \frac {dzo}{dah} …… (7)
$$
بیایید دوباره آن را بشکنیم معادله 7 به شرایط فردی از معادله 3، ما آن را میدانیم:
$$
\frac {dcost}{dao} *\ \frac {dao}{dzo} =\frac {dcost}{dzo} = = ao – y …….. (8)
$$
حالا باید dzo/dah را پیدا کنیم معادله 7که برابر با وزن لایه خروجی مطابق شکل زیر است:
$$
\frac {dzo}{dah} = wo …… (9)
$$
اکنون می توانیم مقدار dcost/dah را با جایگزین کردن مقادیر از پیدا کنیم معادلات 8 و 9 که در معادله 7.
برگشتن به معادله 6، ما هنوز dah/dzh و dzh/dwh را پیدا نکرده ایم.
اولین ترم dah/dzh را می توان به صورت زیر محاسبه کرد:
$$
\frac {dah}{dzh} = sigmoid(zh) * (1-sigmoid(zh)) …….. (10)
$$
و در نهایت، dzh/dwh به سادگی مقادیر ورودی است:
$$
\frac {dzh}{dwh} = ویژگی های ورودی …….. (11)
$$
اگر مقادیر از را جایگزین کنیم معادلات 7، 10 و 11 که در معادله 6، می توانیم ماتریس به روز شده برای وزن لایه های پنهان را دریافت کنیم. برای یافتن مقادیر وزن جدید برای وزنهای لایه پنهان “wh”، مقادیر برگردانده شده توسط معادله 6 را می توان به سادگی با نرخ یادگیری ضرب کرد و از مقادیر وزن لایه پنهان فعلی کم کرد.
به طور مشابه، مشتق تابع هزینه با توجه به بایاس لایه پنهان “bh” به سادگی می تواند به صورت زیر محاسبه شود:
$$
\frac {dcost}{dbh} = \frac {dcost}{dah} *, \frac {dah}{dzh} * \frac {dzh}{dbh} …… (12)
$$
که به سادگی برابر است با:
$$
\frac {dcost}{dbh} = \frac {dcost}{dah} *, \frac {dah}{dzh} …… (13)
$$
زیرا،
$$
\frac {dzh}{dbh} = 1
$$
برای یافتن مقادیر بایاس جدید برای لایه پنهان، مقادیر توسط معادله 13 را می توان به سادگی با نرخ یادگیری ضرب کرد و از مقادیر بایاس لایه پنهان فعلی کم کرد و این برای انتشار به عقب است.
شما می توانید مشاهده کنید که به جلو و عقب انتشار process کاملاً شبیه چیزی است که در آخرین مقالات خود دیدیم. تنها چیزی که ما تغییر دادیم تابع فعال سازی و تابع هزینه است.
کد شبکه های عصبی برای طبقه بندی چند کلاسه
ما تئوری پشت شبکه عصبی را برای طبقهبندی چند طبقه پوشش دادهایم و اکنون زمان آن است که این نظریه را عملی کنیم.
به اسکریپت زیر دقت کنید:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
cat_images = np.random.randn(700, 2) + np.array((0, -3))
mouse_images = np.random.randn(700, 2) + np.array((3, 3))
dog_images = np.random.randn(700, 2) + np.array((-3, 3))
feature_set = np.vstack((cat_images, mouse_images, dog_images))
labels = np.array((0)*700 + (1)*700 + (2)*700)
one_hot_labels = np.zeros((2100, 3))
for i in range(2100):
one_hot_labels(i, labels(i)) = 1
plt.figure(figsize=(10,7))
plt.scatter(feature_set(:,0), feature_set(:,1), c=labels, cmap='plasma', s=100, alpha=0.5)
plt.show()
def sigmoid(x):
return 1/(1+np.exp(-x))
def sigmoid_der(x):
return sigmoid(x) *(1-sigmoid (x))
def softmax(A):
expA = np.exp(A)
return expA / expA.sum(axis=1, keepdims=True)
instances = feature_set.shape(0)
attributes = feature_set.shape(1)
hidden_nodes = 4
output_labels = 3
wh = np.random.rand(attributes,hidden_nodes)
bh = np.random.randn(hidden_nodes)
wo = np.random.rand(hidden_nodes,output_labels)
bo = np.random.randn(output_labels)
lr = 10e-4
error_cost = ()
for epoch in range(50000):
zh = np.dot(feature_set, wh) + bh
ah = sigmoid(zh)
zo = np.dot(ah, wo) + bo
ao = softmax(zo)
dcost_dzo = ao - one_hot_labels
dzo_dwo = ah
dcost_wo = np.dot(dzo_dwo.T, dcost_dzo)
dcost_bo = dcost_dzo
dzo_dah = wo
dcost_dah = np.dot(dcost_dzo , dzo_dah.T)
dah_dzh = sigmoid_der(zh)
dzh_dwh = feature_set
dcost_wh = np.dot(dzh_dwh.T, dah_dzh * dcost_dah)
dcost_bh = dcost_dah * dah_dzh
wh -= lr * dcost_wh
bh -= lr * dcost_bh.sum(axis=0)
wo -= lr * dcost_wo
bo -= lr * dcost_bo.sum(axis=0)
if epoch % 200 == 0:
loss = np.sum(-one_hot_labels * np.log(ao))
print('Loss function value: ', loss)
error_cost.append(loss)
کد بسیار شبیه به کدی است که در مقاله قبلی ایجاد کردیم. در بخش فید فوروارد، تنها تفاوت این است که “ao” که خروجی نهایی است، با استفاده از softmax تابع.
به طور مشابه، در بخش پس انتشار، برای یافتن وزن های جدید برای لایه خروجی، تابع هزینه با توجه به softmax عملکرد به جای sigmoid تابع.
اگر اسکریپت بالا را اجرا کنید، خواهید دید که هزینه خطای نهایی 0.5 خواهد بود. شکل زیر نشان می دهد که چگونه هزینه با تعداد دوره ها کاهش می یابد.

همانطور که می بینید، دوره های زیادی برای رسیدن به هزینه خطای نهایی ما لازم نیست.
به طور مشابه، اگر همان اسکریپت را با تابع sigmoid در لایه خروجی اجرا کنید، حداقل هزینه خطایی که بعد از 50000 دوره به دست می آورید حدود 1.5 خواهد بود که بزرگتر از 0.5 است که با softmax به دست می آید.
نتیجه
شبکه های عصبی دنیای واقعی قادر به حل مسائل طبقه بندی چند طبقه هستند. در این مقاله دیدیم که چگونه می توانیم یک شبکه عصبی بسیار ساده برای طبقه بندی چند کلاسه، از ابتدا در پایتون ایجاد کنیم. این مقاله پایانی این مجموعه است: “شبکه عصبی از ابتدا در پایتون”. در مقالات آینده توضیح خواهم داد که چگونه می توانیم شبکه های عصبی تخصصی تری مانند شبکه های عصبی تکراری و شبکه های عصبی کانولوشنال را از ابتدا در پایتون ایجاد کنیم.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-26 19:43:09



