تجزیه و تحلیل اجزای اصلی (PCA) در پایتون با Scikit-Learn

با در دسترس بودن پردازنده‌ها و پردازنده‌های گرافیکی با کارایی بالا، حل هر رگرسیون، طبقه‌بندی، خوشه‌بندی و سایر مشکلات مرتبط با استفاده از یادگیری ماشین و مدل‌های یادگیری عمیق تقریباً ممکن است. با این حال، هنوز عوامل مختلفی وجود دارد که باعث ایجاد گلوگاه عملکرد در هنگام توسعه چنین مدل‌هایی می‌شود. تعداد زیاد ویژگی ها در مجموعه داده یکی از عواملی است که هم بر زمان آموزش و هم بر دقت مدل های یادگیری ماشین تأثیر می گذارد. شما گزینه های مختلفی برای مقابله با تعداد زیادی ویژگی در یک مجموعه داده دارید.

1. سعی کنید مدل ها را آموزش دهید روی تعداد اصلی ویژگی‌ها، که اگر تعداد ویژگی‌ها خیلی زیاد باشد، روزها یا هفته‌ها طول می‌کشد.
2. با ادغام متغیرهای همبسته، تعداد متغیرها را کاهش دهید.
3. مهم ترین ویژگی ها را از مجموعه داده استخراج کنید که مسئول حداکثر واریانس در خروجی هستند. برای این منظور از تکنیک‌های آماری مختلفی استفاده می‌شود، به‌عنوان مثال، تجزیه و تحلیل متمایز خطی، تحلیل عاملی، و تحلیل مؤلفه‌های اصلی.

در این مقاله خواهیم دید که چگونه تجزیه و تحلیل اجزای اصلی را می توان با استفاده از کتابخانه Scikit-Learn پایتون پیاده سازی کرد.

تجزیه و تحلیل مؤلفه های اصلی

تجزیه و تحلیل مؤلفه اصلی یا PCA، یک تکنیک آماری برای تبدیل داده‌های با ابعاد بالا به داده‌های با ابعاد کم با انتخاب مهم‌ترین ویژگی‌هایی است که حداکثر اطلاعات مربوط به مجموعه داده را به دست می‌آورند. ویژگی ها انتخاب شده اند روی مبنای واریانسی که در خروجی ایجاد می کنند. ویژگی که بیشترین واریانس را ایجاد می کند اولین جزء اصلی است. ویژگی که مسئول دومین واریانس بالاتر است دومین جزء اصلی در نظر گرفته می شود و به همین ترتیب روی. ذکر این نکته ضروری است که اجزای اصلی هیچ ارتباطی با یکدیگر ندارند.

مزایای PCA

دو مزیت اصلی وجود دارد کاهش ابعاد با PCA

1. زمان آموزش الگوریتم ها با تعداد ویژگی های کمتر به میزان قابل توجهی کاهش می یابد.
2. تجزیه و تحلیل داده ها در ابعاد بالا همیشه امکان پذیر نیست. به عنوان مثال اگر 100 ویژگی در یک مجموعه داده وجود دارد. تعداد کل نمودارهای پراکندگی مورد نیاز برای تجسم داده ها خواهد بود 100(100-1)2 = 4950. عملا تجزیه و تحلیل داده ها به این روش امکان پذیر نیست.

عادی سازی ویژگی ها

ذکر این نکته ضروری است که یک مجموعه ویژگی باید قبل از اعمال PCA نرمال شود. به عنوان مثال، اگر مجموعه ای از ویژگی ها دارای داده های بیان شده در واحدهای کیلوگرم، سال نوری یا میلیون ها باشد، مقیاس واریانس در مجموعه آموزشی بسیار زیاد است. اگر PCA اعمال شود روی چنین مجموعه ای از ویژگی ها، بارگیری های حاصل برای ویژگی های با واریانس بالا نیز زیاد خواهد بود. از این رو، مؤلفه‌های اصلی به سمت ویژگی‌هایی با واریانس بالا سوگیری می‌کنند که منجر به نتایج نادرست می‌شود.

در نهایت، آخرین نکته ای که باید قبل از شروع کدنویسی به خاطر بسپاریم این است که PCA یک تکنیک آماری است و فقط می تواند برای داده های عددی اعمال شود. بنابراین، قبل از اعمال PCA، باید ویژگی‌های طبقه‌بندی به ویژگی‌های عددی تبدیل شوند.

پیاده سازی PCA با Scikit-Learn

در این بخش PCA را با کمک پایتون پیاده سازی می کنیم Scikit-Learn کتابخانه ما ابتدا خط لوله یادگیری ماشینی کلاسیک را دنبال خواهیم کرد import کتابخانه‌ها و مجموعه داده‌ها، تجزیه و تحلیل داده‌های اکتشافی و پیش‌پردازش را انجام می‌دهند و در نهایت مدل‌های ما را آموزش می‌دهند، پیش‌بینی می‌کنند و دقت را ارزیابی می‌کنند. تنها مرحله اضافی انجام PCA برای یافتن تعداد بهینه ویژگی ها قبل از آموزش مدل هایمان است. این مراحل به شرح زیر اجرا شده است:

واردات کتابخانه ها

import numpy as np
import pandas as pd

وارد کردن مجموعه داده

مجموعه داده ای که در این مقاله از آن استفاده می کنیم معروف است مجموعه داده عنبیه. برخی از اطلاعات اضافی درباره مجموعه داده Iris در این آدرس موجود است:

https://archive.ics.uci.edu/ml/datasets/iris

مجموعه داده شامل 150 رکورد از گیاه زنبق با چهار ویژگی است: sepal-length، sepal-width، petal-length، و petal-width. همه ویژگی ها عددی هستند. رکوردها به یکی از سه کلاس طبقه بندی شده اند Iris-setosa، Iris-versicolor، یا Iris-virginica.

اسکریپت زیر را برای دانلود مجموعه داده با استفاده از آن اجرا کنید pandas:

url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ('sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class')
dataset = pd.read_csv(url, names=names)

بیایید نگاهی بیاندازیم به اینکه مجموعه داده ما چگونه است:

dataset.head()

با اجرای دستور بالا پنج ردیف اول مجموعه داده ما را مطابق شکل زیر نمایش می دهد:

	به طول کاسبرگ	عرض کاسبرگ	طول گلبرگ	عرض گلبرگ	کلاس
0	5.1	3.5	1.4	0.2	Iris-setosa
1	4.9	3.0	1.4	0.2	Iris-setosa
2	4.7	3.2	1.3	0.2	Iris-setosa
3	4.6	3.1	1.5	0.2	Iris-setosa
4	5.0	3.6	1.4	0.2	Iris-setosa

پیش پردازش

اولین مرحله پیش پردازش، تقسیم مجموعه داده به مجموعه ویژگی ها و برچسب های مربوطه است. اسکریپت زیر این کار را انجام می دهد:

X = dataset.drop('Class', 1)
y = dataset('Class')

اسکریپت بالا مجموعه ویژگی ها را در قسمت ذخیره می کند X متغیر و مجموعه ای از برچسب های مربوطه در به y متغیر.

مرحله پیش پردازش بعدی، تقسیم داده ها به مجموعه های آموزشی و آزمایشی است. برای این کار اسکریپت زیر را اجرا کنید:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

همانطور که قبلا ذکر شد، PCA با مجموعه ویژگی های نرمال شده بهترین عملکرد را دارد. ما نرمال سازی اسکالر استاندارد را برای عادی سازی مجموعه ویژگی های خود انجام خواهیم داد. برای این کار کد زیر را اجرا کنید:

from sklearn.preprocessing import StandardScaler

sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

استفاده از PCA

اجرای PCA با استفاده از کتابخانه Scikit-Learn پایتون تنها به سه خط کد نیاز دارد. را PCA کلاس برای این منظور استفاده می شود. PCA فقط به مجموعه ویژگی ها بستگی دارد و نه داده های برچسب. بنابراین، PCA را می توان به عنوان یک تکنیک یادگیری ماشینی بدون نظارت در نظر گرفت.

انجام PCA با استفاده از Scikit-Learn دو مرحله ای است process:

1. مقداردهی اولیه کنید PCA کلاس با انتقال تعداد مولفه ها به سازنده.
2. با … تماس بگیر fit و سپس transform روش ها را با ارسال ویژگی مجموعه به این متدها انجام دهید. را transform متد تعداد مشخص شده مولفه های اصلی را برمی گرداند.

به کد زیر دقت کنید:

from sklearn.decomposition import PCA

pca = PCA()
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)

در کد بالا، a را ایجاد می کنیم PCA شی به نام pca. ما تعداد اجزای سازنده را مشخص نکردیم. از این رو، هر چهار ویژگی در مجموعه ویژگی‌ها هم برای مجموعه‌های آموزشی و هم برای مجموعه‌های آزمایشی برگردانده می‌شوند.

کلاس PCA شامل explained_variance_ratio_ که واریانس ناشی از هر یک از اجزای اصلی را برمی گرداند. خط کد زیر را برای یافتن «نسبت واریانس توضیح داده شده» اجرا کنید.

explained_variance = pca.explained_variance_ratio_

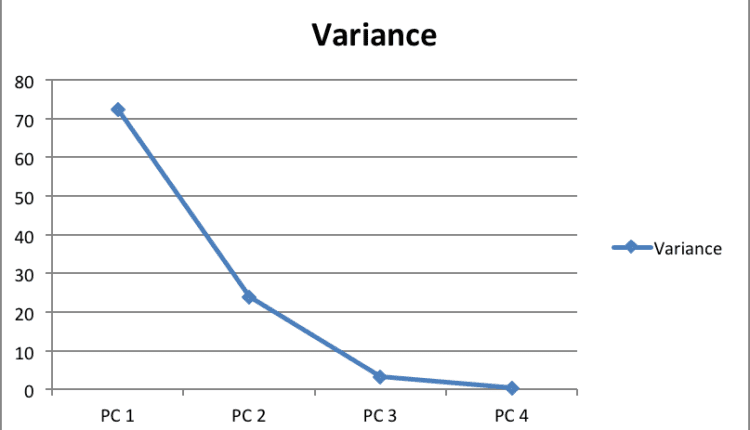
را explained_variance متغیر اکنون یک آرایه از نوع شناور است که شامل نسبت های واریانس برای هر جزء اصلی است. مقادیر برای explained_variance متغیر به شکل زیر است:

0.722265

0.239748

0.0333812

0.0046056

مشاهده می شود که اولین مؤلفه اصلی مسئول 22/72 درصد واریانس است. به طور مشابه، مولفه اصلی دوم باعث ایجاد 23.9٪ واریانس در مجموعه داده می شود. در مجموع می توان گفت که (72.22 + 23.9) 96.21 درصد از اطلاعات طبقه بندی موجود در مجموعه ویژگی ها توسط دو جزء اصلی اول گرفته شده است.

بیایید ابتدا سعی کنیم از 1 جزء اصلی برای آموزش الگوریتم خود استفاده کنیم. برای این کار کد زیر را اجرا کنید:

from sklearn.decomposition import PCA

pca = PCA(n_components=1)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)

بقیه ی process سرراست است

آموزش و پیش بینی

در این مورد ما از طبقه بندی جنگل تصادفی برای پیش بینی استفاده می کنیم.

from sklearn.ensemble import RandomForestClassifier

classifier = RandomForestClassifier(max_depth=2, random_state=0)
classifier.fit(X_train, y_train)


y_pred = classifier.predict(X_test)

سنجش عملکرد

from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score

cm = confusion_matrix(y_test, y_pred)
print(cm)
print('Accuracy' + accuracy_score(y_test, y_pred))

خروجی اسکریپت بالا به شکل زیر است:

((11  0  0)
 ( 0 12  1)
 ( 0  1  5))
0.933333333333

از خروجی می توان دریافت که تنها با یک ویژگی، الگوریتم جنگل تصادفی قادر است 28 مورد از 30 نمونه را به درستی پیش بینی کند که در نتیجه دقت 93.33 درصد را به همراه دارد.

نتایج با 2 و 3 مؤلفه اصلی

حال بیایید سعی کنیم عملکرد طبقه بندی الگوریتم جنگل تصادفی را با 2 جزء اصلی ارزیابی کنیم. این قطعه کد را به روز کنید:

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)

در اینجا تعداد مؤلفه‌ها برای PCA روی 2 تنظیم شده است. نتایج طبقه‌بندی با 2 مؤلفه به شرح زیر است:

((11  0  0)
 ( 0 10  3)
 ( 0  2  4))
0.833333333333

با دو جزء اصلی، دقت طبقه‌بندی به 83.33% در مقایسه با 93.33% برای 1 جزء کاهش می‌یابد.

با سه جزء اصلی، نتیجه به این صورت است:

((11  0  0)
 ( 0 12  1)
 ( 0  1  5))
0.933333333333

با سه جزء اصلی، دقت طبقه بندی مجدداً به 93.33 درصد افزایش می یابد.

نتایج با مجموعه ویژگی کامل

بیایید سعی کنیم نتایج را با یک مجموعه ویژگی کامل پیدا کنیم. برای انجام این کار، به سادگی قسمت PCA را از اسکریپتی که در بالا نوشتیم حذف کنید. نتایج با مجموعه ویژگی های کامل، بدون اعمال PCA به این صورت است:

((11  0  0)
 ( 0 13  0)
 ( 0  2  4))
0.933333333333

دقت دریافتی با مجموعه ویژگی کامل برای الگوریتم جنگل تصادفی نیز 93.33 درصد است.

بحث

از آزمایش فوق ما به سطح بهینه ای از دقت دست یافتیم در حالی که به طور قابل توجهی تعداد ویژگی های مجموعه داده را کاهش دادیم. دیدیم که دقت به دست آمده با تنها 1 جزء اصلی برابر است با دقت به دست آمده با مجموعه ویژگی یعنی 93.33%. همچنین لازم به ذکر است که دقت طبقه‌بندی‌کننده لزوماً با افزایش تعداد اجزای اصلی بهبود نمی‌یابد. از نتایج می توان دریافت که دقت به دست آمده با یک مولفه اصلی (33/93 درصد) بیشتر از دقت به دست آمده با دو مؤلفه اصلی (33/83 درصد) بود.

تعداد اجزای اصلی برای حفظ در یک مجموعه ویژگی بستگی دارد روی شرایط متعددی مانند ظرفیت ذخیره سازی، زمان آموزش، عملکرد، و غیره. در برخی از مجموعه داده ها، همه ویژگی ها به طور یکسان در واریانس کلی نقش دارند، بنابراین همه اجزای اصلی برای پیش بینی ها بسیار مهم هستند و هیچ کدام را نمی توان نادیده گرفت. یک قانون کلی این است که تعداد مؤلفه‌های اصلی را که به واریانس قابل توجه کمک می‌کنند، در نظر بگیرید و مؤلفه‌هایی را که بازده واریانس کاهشی دارند نادیده بگیرید. یک راه خوب این است که واریانس را در برابر اجزای اصلی رسم کنید و اجزای اصلی را با مقادیر کاهشی نادیده بگیرید همانطور که در نمودار زیر نشان داده شده است:

به عنوان مثال، در نمودار بالا، می بینیم که بعد از سومین جزء اصلی، تغییر واریانس تقریباً کاهش می یابد. بنابراین، سه جزء اول را می توان انتخاب کرد.