از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
تجزیه و تحلیل فرضیه های آماری در پایتون با ANOVA، مجذور کای و همبستگی پیرسون
سرفصلهای مطلب
معرفی
پایتون یک زبان فوق العاده همه کاره است که برای کارهای مختلف در طیف وسیعی از رشته ها مفید است. یکی از این رشته ها، تحلیل آماری است روی مجموعه داده ها و در کنار SPSS، پایتون یکی از رایج ترین ابزارهای آمار است.
ماهیت کاربرپسند و شهودی پایتون اجرای تست های آماری و پیاده سازی تکنیک های تحلیلی را به ویژه از طریق استفاده از statsmodels کتابخانه.
معرفی کتابخانه statsmodels در پایتون
این statsmodels کتابخانه یک ماژول برای پایتون است که دسترسی آسان به انواع ابزارهای آماری برای انجام تست های آماری و کاوش داده ها را می دهد. تعدادی تست و توابع آماری وجود دارد که کتابخانه به آنها دسترسی می دهد، از جمله رگرسیون حداقل مربعات معمولی (OLS)، مدل های خطی تعمیم یافته، مدل های لاجیت، تجزیه و تحلیل مؤلفه های اصلی (PCA)، و میانگین متحرک یکپارچه خودرگرسیون مدل های (ARIMA).
نتایج مدل ها به طور مداوم در برابر سایر بسته های آماری آزمایش می شوند تا از دقت مدل ها اطمینان حاصل شود. هنگامی که با SciPy و پانداها، تجسم داده ها، اجرای آزمایش های آماری و بررسی روابط از نظر اهمیت بسیار ساده است.
انتخاب یک مجموعه داده
قبل از اینکه بتوانیم آمار را با پایتون تمرین کنیم، باید یک مجموعه داده را انتخاب کنیم. ما از مجموعه داده های گردآوری شده توسط بنیاد Gapminder استفاده خواهیم کرد.
مجموعه داده Gapminder بسیاری از متغیرهای مورد استفاده برای ارزیابی سلامت عمومی و تندرستی جمعیت در کشورهای سراسر جهان را ردیابی می کند. ما از مجموعه داده استفاده خواهیم کرد زیرا بسیار مستند، استاندارد و کامل است. برای استفاده از آن، نیازی به انجام کارهای زیادی در زمینه پیش پردازش نخواهیم داشت.
چند کار وجود دارد که ما می خواهیم انجام دهیم تا مجموعه داده را برای اجرای رگرسیون ها، ANOVA ها و آزمایش های دیگر آماده کنیم، اما به طور کلی مجموعه داده آماده کار است.
نقطه شروع برای تجزیه و تحلیل آماری ما از مجموعه داده Gapminder، تجزیه و تحلیل داده های اکتشافی است. ما از برخی توابع نمودار و رسم از Matplotlib و Seaborn برای تجسم برخی از روابط جالب استفاده خواهیم کرد و ایده ای از روابط متغیرهایی که ممکن است بخواهیم بررسی کنیم به دست می آوریم.
تجزیه و تحلیل داده های اکتشافی و پیش پردازش
ما با تجسم برخی از روابط ممکن شروع می کنیم. با استفاده از Seaborn و Pandas میتوانیم رگرسیونهایی انجام دهیم که به قدرت همبستگی بین متغیرهای موجود در مجموعه دادهمان نگاه میکند تا ایدهای در مورد اینکه کدام روابط متغیر ارزش مطالعه دارند را به دست آوریم.
خوب import آن دو و هر کتابخانه دیگری که در اینجا استفاده خواهیم کرد:
import statsmodels.formula.api as smf
import statsmodels.stats.multicomp as multi
import scipy
from scipy.stats import pearsonr
import pandas as pd
from seaborn import regplot
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
پیش پردازش زیادی وجود ندارد که باید انجام دهیم، اما باید چند کار را انجام دهیم. ابتدا، ما گم شدن یا را بررسی می کنیم null داده و هر ورودی غیر عددی را به عددی تبدیل کنید. ما همچنین یک کپی از دیتافریم تغییر یافته که با آن کار خواهیم کرد تهیه خواهیم کرد:
def check_missing_values(df, cols):
for col in cols:
print("Column {} is missing:".format(col))
print((df(col).values == ' ').sum())
print()
def convert_numeric(dataframe, cols):
for col in cols:
dataframe(col) = pd.to_numeric(dataframe(col), errors='coerce')
df = pd.read_csv("gapminder.csv")
print("Null values:")
print(df.isnull().values.any())
cols = ('lifeexpectancy', 'breastcancerper100th', 'suicideper100th')
norm_cols = ('internetuserate', 'employrate')
df2 = df.copy()
check_missing_values(df, cols)
check_missing_values(df, norm_cols)
convert_numeric(df2, cols)
convert_numeric(df2, norm_cols)
در اینجا خروجی ها آمده است:
Null values:
Column lifeexpectancy is missing:
22
Column breastcancerper100th is missing:
40
Column suicideper100th is missing:
22
Column internetuserate is missing:
21
Column employrate is missing:
35
تعداد انگشت شماری از مقادیر گم شده وجود دارد، اما تبدیل عددی ما باید آنها را به آنها تبدیل کند NaN مقادیر، اجازه می دهد تا تجزیه و تحلیل داده های اکتشافی انجام شود روی مجموعه داده
به طور خاص، میتوانیم رابطه بین نرخ استفاده از اینترنت و امید به زندگی، یا بین نرخ استفاده از اینترنت و نرخ اشتغال را تجزیه و تحلیل کنیم. بیایید سعی کنیم نمودارهای جداگانه برخی از این روابط را با استفاده از Seaborn و Matplotlib ایجاد کنیم:
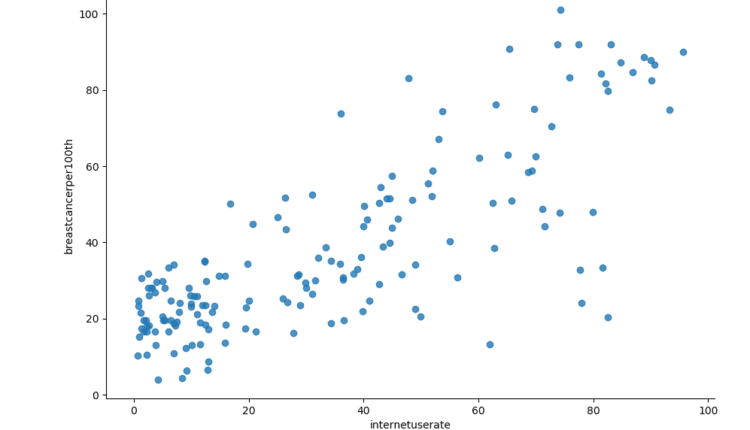
sns.lmplot(x="internetuserate", y="breastcancerper100th", data=df2, fit_reg=False)
plt.title("Internet Use Rate and Breast Cancer Per 100k")
plt.show()
sns.lmplot(x="internetuserate", y="lifeexpectancy", data=df2, fit_reg=False)
plt.title("Internet Use Rate and Life Expectancy")
plt.show()
sns.lmplot(x="internetuserate", y="employrate", data=df2, fit_reg=False)
plt.title("Internet Use Rate and Employment Rate")
plt.show()
در اینجا نتایج نمودارها آمده است:



به نظر می رسد روابط جالبی وجود دارد که می توانیم آنها را بیشتر بررسی کنیم. جالب اینجاست که به نظر میرسد یک رابطه مثبت نسبتاً قوی بین میزان استفاده از اینترنت و سرطان سینه وجود دارد، اگرچه این احتمالاً تنها نمونهای از آزمایش بهتر در کشورهایی است که دسترسی بیشتری به فناوری دارند.
همچنین به نظر می رسد یک رابطه نسبتاً قوی، هرچند خطی کمتر بین امید به زندگی و میزان استفاده از اینترنت وجود دارد.
در نهایت، به نظر می رسد که یک رابطه سهموی و غیر خطی بین نرخ استفاده از اینترنت و نرخ اشتغال وجود دارد.
انتخاب یک فرضیه مناسب
ما می خواهیم رابطه ای را انتخاب کنیم که شایستگی کاوش بیشتر را دارد. در اینجا روابط بالقوه زیادی وجود دارد که میتوانیم در مورد آنها فرضیهای ایجاد کنیم و با آزمونهای آماری رابطه را بررسی کنیم. وقتی فرضیه میکنیم و بین دو متغیر آزمون همبستگی اجرا میکنیم، اگر آزمون همبستگی معنادار است، باید آزمونهای آماری انجام دهیم تا ببینیم چقدر همبستگی قوی است و آیا میتوانیم به طور قابل اعتماد بگوییم که همبستگی بین دو متغیر وجود دارد یا خیر. چیزی بیش از شانس است
نوع آزمون آماری مورد استفاده ما بستگی دارد روی ماهیت متغیرهای توضیحی و پاسخ ما، همچنین شناخته شده و متغیرهای مستقل و وابسته. ما به روش اجرای سه نوع مختلف تست آماری خواهیم پرداخت:
- ANOVA ها
- تست های مربع کای
- رگرسیون ها
ما با آنچه در بالا تجسم کردیم پیش می رویم و رابطه بین نرخ استفاده از اینترنت و امید به زندگی را بررسی می کنیم.
این فرضیه صفر این است که بین میزان استفاده از اینترنت و امید به زندگی رابطه معناداری وجود ندارد، در حالی که فرضیه ما وجود دارد است رابطه بین دو متغیر
ما انواع مختلفی از آزمون های فرضیه را انجام خواهیم داد روی مجموعه داده نوع آزمون فرضیه ای که استفاده می کنیم وابسته است روی ماهیت متغیرهای توضیحی و پاسخ ما. ترکیب های مختلف متغیرهای توضیحی و پاسخ نیاز به آزمون های آماری متفاوتی دارند. به عنوان مثال، اگر یک متغیر مقوله ای و یک متغیر ماهیت کمی داشته باشد، an تحلیل واریانس مورد نیاز است.
تجزیه و تحلیل واریانس (ANOVA)
یک تجزیه و تحلیل واریانس (ANOVA) یک آزمون آماری است که برای مقایسه دو یا چند میانگین با هم استفاده می شود که از طریق تحلیل واریانس تعیین می شود. آزمون های ANOVA یک طرفه برای تجزیه و تحلیل تفاوت بین گروه ها و تعیین اینکه آیا تفاوت ها از نظر آماری معنی دار هستند یا خیر، استفاده می شود.
ANOVAهای یک طرفه دو یا چند میانگین گروه مستقل را با هم مقایسه می کنند، اگرچه در عمل اغلب زمانی استفاده می شوند که حداقل سه گروه مستقل وجود داشته باشد.
به منظور انجام ANOVA روی مجموعه داده Gapminder، ما باید برخی از ویژگیها را تغییر دهیم، زیرا این مقادیر در مجموعه داده پیوسته هستند، اما تجزیه و تحلیل ANOVA برای موقعیتهایی که یک متغیر طبقهبندی و یک متغیر کمی است مناسب است.
ما میتوانیم دادهها را از پیوسته به کمی با انتخاب یک دسته و ترکیب متغیر مورد نظر و تقسیم آن به صدک تبدیل کنیم. متغیر مستقل به یک متغیر طبقه ای تبدیل می شود، در حالی که متغیر وابسته پیوسته می ماند. ما می توانیم استفاده کنیم qcut() در پانداها برای تقسیم دیتافریم به bin ها عمل می کند:
def bin(dataframe, cols):
for col in cols:
new_col_name = "{}_bins".format(col)
dataframe(new_col_name) = pd.qcut(dataframe(col), 10, labels=("1=10%", "2=20%", "3=30%", "4=40%", "5=50%", "6=60%", "7=70%", "8=80", "9=90%", "10=100%"))
df3 = df2.copy()
bin(df3, cols)
bin(df3, norm_cols)
پس از تبدیل متغیرها و آماده شدن برای تجزیه و تحلیل، می توانیم از آن استفاده کنیم statsmodel کتابخانه برای انجام ANOVA روی ویژگی های انتخاب شده خوب print نتایج ANOVA را بررسی کنید و بررسی کنید که آیا رابطه بین دو متغیر از نظر آماری معنادار است یا خیر:
anova_df = df3(('lifeexpectancy', 'internetuserate_bins', 'employrate_bins')).dropna()
relate_df = df3(('lifeexpectancy', 'internetuserate_bins'))
anova = smf.ols(formula='lifeexpectancy ~ C(internetuserate_bins)', data=anova_df).fit()
print(anova.summary())
mean = relate_df.groupby("internetuserate_bins").mean()
sd = relate_df.groupby("internetuserate_bins").std()
print(mean)
print(sd)
این هم خروجی مدل:
OLS Regression Results
==============================================================================
Dep. Variable: lifeexpectancy R-squared: 0.689
Model: OLS Adj. R-squared: 0.671
Method: Least Squares F-statistic: 38.65
Date: Mon, 11 May 2020 Prob (F-statistic): 1.71e-35
Time: 17:49:24 Log-Likelihood: -521.54
No. Observations: 167 AIC: 1063.
Df Residuals: 157 BIC: 1094.
Df Model: 9
Covariance Type: nonrobust
======================================================================================================
coef std err t P>|t| (0.025 0.975)
------------------------------------------------------------------------------------------------------
Intercept 56.6603 1.268 44.700 0.000 54.157 59.164
C(internetuserate_bins)(T.2=20%) 1.6785 1.870 0.898 0.371 -2.015 5.372
C(internetuserate_bins)(T.3=30%) 5.5273 1.901 2.907 0.004 1.772 9.283
C(internetuserate_bins)(T.4=40%) 11.5693 1.842 6.282 0.000 7.932 15.207
C(internetuserate_bins)(T.5=50%) 14.6991 1.870 7.860 0.000 11.005 18.393
C(internetuserate_bins)(T.6=60%) 16.7287 1.870 8.946 0.000 13.035 20.422
C(internetuserate_bins)(T.7=70%) 17.8802 1.975 9.052 0.000 13.978 21.782
C(internetuserate_bins)(T.8=80) 19.8302 1.901 10.430 0.000 16.075 23.586
C(internetuserate_bins)(T.9=90%) 23.0723 1.901 12.135 0.000 19.317 26.828
C(internetuserate_bins)(T.10=100%) 23.3042 1.901 12.257 0.000 19.549 27.060
==============================================================================
Omnibus: 10.625 Durbin-Watson: 1.920
Prob(Omnibus): 0.005 Jarque-Bera (JB): 11.911
Skew: -0.484 Prob(JB): 0.00259
Kurtosis: 3.879 Cond. No. 10.0
==============================================================================
Warnings:
(1) Standard Errors assume that the covariance matrix of the errors is correctly specified.
می بینیم که مدل یک مقدار P بسیار کوچک (آماره پروب F) از 1.71e-35. این بسیار کمتر از آستانه اهمیت معمول است 0.05بنابراین نتیجه می گیریم که بین امید به زندگی و میزان استفاده از اینترنت رابطه معناداری وجود دارد.
از آنجایی که به نظر می رسد همبستگی P-value مهم است، و از آنجایی که ما 10 دسته مختلف داریم، می خواهیم یک تست تعقیبی را اجرا کنیم تا بررسی کنیم که تفاوت بین میانگین ها همچنان قابل توجه است حتی پس از بررسی نوع 1. خطاها ما میتوانیم آزمایشهای پسهک را با کمک انجام دهیم multicomp ماژول، با استفاده از a Tukey صادقانه تفاوت قابل توجهی تست (Tukey HSD):
multi_comparison = multi.MultiComparison(anova_df("lifeexpectancy"), anova_df("internetuserate_bins"))
results = multi_comparison.tukeyhsd()
print(results)
در اینجا نتایج آزمایش آمده است:
Multiple Comparison of Means - Tukey HSD, FWER=0.05
=======================================================
group1 group2 meandiff p-adj lower upper reject
-------------------------------------------------------
10=100% 1=10% -23.3042 0.001 -29.4069 -17.2015 True
10=100% 2=20% -21.6257 0.001 -27.9633 -15.2882 True
10=100% 3=30% -17.7769 0.001 -24.2097 -11.344 True
10=100% 4=40% -11.7349 0.001 -17.9865 -5.4833 True
10=100% 5=50% -8.6051 0.001 -14.9426 -2.2676 True
10=100% 6=60% -6.5755 0.0352 -12.913 -0.238 True
10=100% 7=70% -5.4241 0.2199 -12.0827 1.2346 False
10=100% 8=80 -3.4741 0.7474 -9.9069 2.9588 False
10=100% 9=90% -0.2319 0.9 -6.6647 6.201 False
1=10% 2=20% 1.6785 0.9 -4.3237 7.6807 False
1=10% 3=30% 5.5273 0.1127 -0.5754 11.6301 False
1=10% 4=40% 11.5693 0.001 5.6579 17.4807 True
1=10% 5=50% 14.6991 0.001 8.6969 20.7013 True
1=10% 6=60% 16.7287 0.001 10.7265 22.7309 True
1=10% 7=70% 17.8801 0.001 11.5399 24.2204 True
1=10% 8=80 19.8301 0.001 13.7274 25.9329 True
1=10% 9=90% 23.0723 0.001 16.9696 29.1751 True
2=20% 3=30% 3.8489 0.6171 -2.4887 10.1864 False
2=20% 4=40% 9.8908 0.001 3.7374 16.0443 True
2=20% 5=50% 13.0206 0.001 6.7799 19.2614 True
2=20% 6=60% 15.0502 0.001 8.8095 21.291 True
2=20% 7=70% 16.2017 0.001 9.6351 22.7683 True
2=20% 8=80 18.1517 0.001 11.8141 24.4892 True
2=20% 9=90% 21.3939 0.001 15.0563 27.7314 True
3=30% 4=40% 6.042 0.0678 -0.2096 12.2936 False
3=30% 5=50% 9.1718 0.001 2.8342 15.5093 True
3=30% 6=60% 11.2014 0.001 4.8638 17.5389 True
3=30% 7=70% 12.3528 0.001 5.6942 19.0114 True
3=30% 8=80 14.3028 0.001 7.87 20.7357 True
3=30% 9=90% 17.545 0.001 11.1122 23.9778 True
4=40% 5=50% 3.1298 0.8083 -3.0237 9.2833 False
4=40% 6=60% 5.1594 0.1862 -0.9941 11.3129 False
4=40% 7=70% 6.3108 0.0638 -0.1729 12.7945 False
4=40% 8=80 8.2608 0.0015 2.0092 14.5124 True
4=40% 9=90% 11.503 0.001 5.2514 17.7546 True
5=50% 6=60% 2.0296 0.9 -4.2112 8.2704 False
5=50% 7=70% 3.181 0.8552 -3.3856 9.7476 False
5=50% 8=80 5.131 0.2273 -1.2065 11.4686 False
5=50% 9=90% 8.3732 0.0015 2.0357 14.7108 True
6=60% 7=70% 1.1514 0.9 -5.4152 7.718 False
6=60% 8=80 3.1014 0.8456 -3.2361 9.439 False
6=60% 9=90% 6.3436 0.0496 0.0061 12.6812 True
7=70% 8=80 1.95 0.9 -4.7086 8.6086 False
7=70% 9=90% 5.1922 0.2754 -1.4664 11.8508 False
8=80 9=90% 3.2422 0.8173 -3.1907 9.675 False
-------------------------------------------------------
اکنون ما بینش بهتری در مورد اینکه کدام گروه ها در مقایسه ما تفاوت های آماری معنی داری دارند، داریم.
اگر reject ستون دارای یک برچسب از False، می دانیم که توصیه می شود این را رد کنیم فرضیه صفر و فرض کنید که بین دو گروه مورد مقایسه تفاوت معناداری وجود دارد.
آزمون Chi-Square استقلال
ANOVA برای مواردی مناسب است که یک متغیر پیوسته و دیگری مقوله ای است. اکنون به بررسی روش اجرای a می پردازیم آزمون کای اسکوئر استقلال.
آزمون کای اسکوئر استقلال زمانی استفاده می شود که متغیرهای توضیحی و پاسخی مقوله ای باشند. شما به احتمال زیاد می خواهید از تست Chi-Square زمانی که متغیر توضیحی کمی و متغیر پاسخ طبقه بندی می شود استفاده کنید، که می توانید با تقسیم متغیر توضیحی به دسته ها انجام دهید.
آزمون کای اسکوئر استقلال یک آزمون آماری است که برای تجزیه و تحلیل میزان رابطه معنادار بین دو متغیر طبقهبندی استفاده میشود. هنگامی که آزمون Chi-Square اجرا می شود، هر دسته در یک متغیر بسامد خود را با دسته های متغیر دوم مقایسه می کند. این به این معنی است که داده ها می توانند به عنوان یک جدول فرکانس نمایش داده شوند، جایی که ردیف ها نشان دهنده متغیرهای مستقل و ستون ها نشان دهنده متغیرهای وابسته هستند.
درست مانند اینکه ما متغیر مستقل خود را به یک متغیر طبقه بندی تبدیل کردیم (با باینینگ کردن آن)، برای آزمون ANOVA، برای انجام تست Chi-Square باید هر دو متغیر را طبقه بندی کنیم. فرضیه ما برای این مشکل همانند فرضیه مسئله قبلی است که بین امید به زندگی و میزان استفاده از اینترنت رابطه معناداری وجود دارد.
فعلاً همه چیز را ساده نگه میداریم و متغیر نرخ استفاده از اینترنت خود را به دو دسته تقسیم میکنیم، اگرچه به راحتی میتوانیم کارهای بیشتری انجام دهیم. ما یک تابع برای رسیدگی به آن می نویسیم.
ما برای محافظت در برابر خطاهای نوع 1 (مثبت نادرست) با استفاده از رویکردی به نام تنظیم بونفرونی. برای انجام این کار، می توانید مقایسه هایی را برای جفت های مختلف ممکن از متغیر پاسخ خود انجام دهید و سپس اهمیت تنظیم شده آنها را بررسی کنید.
ما در اینجا مقایسهای را برای همه جفتهای ممکن مختلف انجام نمیدهیم، فقط نشان میدهیم که چگونه میتوان این کار را انجام داد. ما چند مقایسه مختلف با استفاده از یک طرح کدگذاری مجدد انجام می دهیم و رکوردها را در ستون های ویژگی جدید ترسیم می کنیم.
پس از آن، می توانیم تعداد مشاهده شده را بررسی کنیم و جداول آن مقایسه ها را ایجاد کنیم:
def half_bin(dataframe, cols):
for col in cols:
new_col_name = "{}_bins_2".format(col)
dataframe(new_col_name) = pd.qcut(dataframe(col), 2, labels=("1=50%", "2=100%"))
half_bin(df3, ('internetuserate'))
recode_2 = {"3=30%": "3=30%", "7=70%": "7=70%"}
recode_3 = {"2=20%": "2=20%", "8=80": "8=80"}
recode_4 = {"6=60%": "6=60%", "9=90%": "9=90%"}
recode_5 = {"4=40%": "4=40%", "7=70%": "7=70%"}
df3('Comp_3v7') = df3('lifeexpectancy_bins').map(recode_2)
df3('Comp_2v8') = df3('lifeexpectancy_bins').map(recode_3)
df3('Comp_6v9') = df3('lifeexpectancy_bins').map(recode_4)
df3('Comp_4v7') = df3('lifeexpectancy_bins').map(recode_5)
اجرای آزمون Chi-Square و مقایسه پس از آن ابتدا شامل ساخت جدول مقایسه بین زبانه ها می شود. جدول مقایسه زبانه های متقاطع درصد وقوع متغیر پاسخ را برای سطوح مختلف متغیر توضیحی نشان می دهد.
فقط برای اینکه ایده ای از روش کار این کار داشته باشیم، بیایید print نتایج را برای همه مقایسههای سطل امید به زندگی نشان دهید:
count_table = pd.crosstab(df3('internetuserate_bins_2'), df3('lifeexpectancy_bins'))
print(count_table)
lifeexpectancy_bins 1=10% 2=20% 3=30% 4=40% ... 7=70% 8=80 9=90% 10=100%
internetuserate_bins_2 ...
1=50% 18 19 16 14 ... 4 4 1 0
2=100% 0 0 1 4 ... 15 11 16 19
میتوانیم ببینیم که مقایسه بین زبانهها فراوانی دستههای یک متغیر را در متغیر دوم بررسی میکند. در بالا، توزیع امید به زندگی را در موقعیت هایی مشاهده می کنیم که در یکی از دو سطل زباله ای که ما ایجاد کردیم قرار می گیرند.
اکنون باید زبانه های متقاطع را برای جفت های مختلفی که در بالا ایجاد کردیم محاسبه کنیم، زیرا این همان چیزی است که در آزمون Chi-Square اجرا می کنیم:
count_table_3 = pd.crosstab(df3('internetuserate_bins_2'), df3('Comp_3v7'))
count_table_4 = pd.crosstab(df3('internetuserate_bins_2'), df3('Comp_2v8'))
count_table_5 = pd.crosstab(df3('internetuserate_bins_2'), df3('Comp_6v9'))
count_table_6 = pd.crosstab(df3('internetuserate_bins_2'), df3('Comp_4v7'))
هنگامی که متغیرها را به گونهای تبدیل کردیم که تست Chi-Square قابل انجام باشد، میتوانیم از آن استفاده کنیم chi2_contingency عملکرد در statsmodel برای انجام آزمایش
ما می خواهیم که print درصدهای ستون و همچنین نتایج آزمون Chi-Square را خارج کنید، و ما یک تابع برای انجام این کار ایجاد خواهیم کرد. سپس از تابع خود برای انجام تست Chi-Square برای چهار جدول مقایسه ای که ایجاد کردیم استفاده می کنیم:
def chi_sq_test(table):
print("Results for:")
print(str(table))
col_sum = table.sum(axis=0)
col_percents = table/col_sum
print(col_percents)
chi_square = scipy.stats.chi2_contingency(table)
print("Chi-square value, p-value, expected_counts")
print(chi_square)
print()
print("Initial Chi-square:")
chi_sq_test(count_table)
print(" ")
chi_sq_test(count_table_3)
chi_sq_test(count_table_4)
chi_sq_test(count_table_5)
chi_sq_test(count_table_6)
در اینجا نتایج آمده است:
Initial Chi-square:
Results for:
lifeexpectancy_bins 1=10% 2=20% 3=30% 4=40% ... 7=70% 8=80 9=90% 10=100%
internetuserate_bins_2 ...
1=50% 18 19 16 14 ... 4 4 1 0
2=100% 0 0 1 4 ... 15 11 16 19
(2 rows x 10 columns)
lifeexpectancy_bins 1=10% 2=20% 3=30% ... 8=80 9=90% 10=100%
internetuserate_bins_2 ...
1=50% 1.0 1.0 0.941176 ... 0.266667 0.058824 0.0
2=100% 0.0 0.0 0.058824 ... 0.733333 0.941176 1.0
(2 rows x 10 columns)
Chi-square value, p-value, expected_counts
(102.04563740451277, 6.064860600653971e-18, 9, array(((9.45251397, 9.97765363, 8.9273743 , 9.45251397, 9.45251397,
9.97765363, 9.97765363, 7.87709497, 8.9273743 , 9.97765363),
(8.54748603, 9.02234637, 8.0726257 , 8.54748603, 8.54748603,
9.02234637, 9.02234637, 7.12290503, 8.0726257 , 9.02234637))))
-----
Results for:
Comp_3v7 3=30% 7=70%
internetuserate_bins_2
1=50% 16 4
2=100% 1 15
Comp_3v7 3=30% 7=70%
internetuserate_bins_2
1=50% 0.941176 0.210526
2=100% 0.058824 0.789474
Chi-square value, p-value, expected_counts
(16.55247678018576, 4.7322137795376575e-05, 1, array((( 9.44444444, 10.55555556),
( 7.55555556, 8.44444444))))
-----
Results for:
Comp_2v8 2=20% 8=80
internetuserate_bins_2
1=50% 19 4
2=100% 0 11
Comp_2v8 2=20% 8=80
internetuserate_bins_2
1=50% 1.0 0.266667
2=100% 0.0 0.733333
Chi-square value, p-value, expected_counts
(17.382650301643437, 3.0560286589975315e-05, 1, array(((12.85294118, 10.14705882),
( 6.14705882, 4.85294118))))
-----
Results for:
Comp_6v9 6=60% 9=90%
internetuserate_bins_2
1=50% 6 1
2=100% 13 16
Comp_6v9 6=60% 9=90%
internetuserate_bins_2
1=50% 0.315789 0.058824
2=100% 0.684211 0.941176
Chi-square value, p-value, expected_counts
(2.319693757720874, 0.12774517376836148, 1, array((( 3.69444444, 3.30555556),
(15.30555556, 13.69444444))))
-----
Results for:
Comp_4v7 4=40% 7=70%
internetuserate_bins_2
1=50% 14 4
2=100% 4 15
Comp_4v7 4=40% 7=70%
internetuserate_bins_2
1=50% 0.777778 0.210526
2=100% 0.222222 0.789474
Chi-square value, p-value, expected_counts
(9.743247922437677, 0.0017998260000241526, 1, array(((8.75675676, 9.24324324),
(9.24324324, 9.75675676))))
-----
اگر ما فقط به نتایج جدول شمارش کامل نگاه کنیم، به نظر می رسد که یک مقدار P از 6.064860600653971e-18.
با این حال، برای اطمینان از اینکه چگونه گروههای مختلف از یکدیگر جدا میشوند، باید آزمون Chi-Square را برای جفتهای مختلف در چارچوب دادهمان انجام دهیم. ما بررسی می کنیم که آیا تفاوت آماری معنی داری برای هر یک از جفت های مختلف انتخاب شده وجود دارد یا خیر. توجه داشته باشید که مقدار P که یک نتیجه قابل توجه را نشان می دهد بسته به آن تغییر می کند روی چقدر مقایسه می کنید، و در حالی که ما در این آموزش به آن نمی پردازیم، باید به آن توجه داشته باشید.
مقایسه 6 در مقابل 9 مقدار P را به ما می دهد 0.127، که بالاتر از 0.05 آستانه، نشان می دهد که تفاوت برای آن دسته ممکن است غیر قابل توجه باشد. دیدن تفاوتهای مقایسهها به ما کمک میکند بفهمیم چرا باید سطوح مختلف را با یکدیگر مقایسه کنیم.
همبستگی پیرسون
ما تستی را که باید در هنگام داشتن یک متغیر توضیحی طبقهای و یک متغیر پاسخ کمی (ANOVA) استفاده کنید، و همچنین تستی را که در صورت داشتن دو متغیر طبقهبندی (Chi-Squared) استفاده میکنید، پوشش دادهایم.
اکنون نگاهی خواهیم داشت به نوع آزمون مناسب برای استفاده زمانی که یک متغیر توضیحی کمی و یک متغیر پاسخ کمی دارید – همبستگی پیرسون.
همبستگی پیرسون آزمون برای تجزیه و تحلیل قدرت رابطه بین دو متغیر ارائه شده، هر دو از نظر ماهیت کمی استفاده می شود. مقدار، یا قدرت همبستگی پیرسون، بین خواهد بود +1 و -1.
همبستگی 1 نشان دهنده ارتباط کامل بین متغیرها است و همبستگی مثبت یا منفی است. ضرایب همبستگی نزدیک به 0 نشان دهنده همبستگی های بسیار ضعیف، تقریباً وجود ندارد. در حالی که روش های دیگری برای اندازه گیری همبستگی بین دو متغیر وجود دارد، مانند همبستگی اسپیرمن یا همبستگی رتبه کندال، همبستگی پیرسون احتمالاً رایج ترین آزمون همبستگی است.
از آنجایی که مجموعه داده Gapminder ویژگی های خود را با متغیرهای کمی نشان می دهد، قبل از اجرای همبستگی پیرسون نیازی به تغییر دسته بندی داده ها نداریم. روی آی تی. توجه داشته باشید که فرض بر این است که هر دو متغیر به طور معمول توزیع شده اند و مقادیر پرت قابل توجهی در مجموعه داده وجود ندارد. برای انجام همبستگی پیرسون به SciPy نیاز داریم.
ما رابطه بین امید به زندگی و نرخ استفاده از اینترنت و همچنین نرخ استفاده از اینترنت و نرخ اشتغال را نمودار خواهیم کرد تا ببینیم نمودار همبستگی دیگری ممکن است چگونه باشد. پس از ایجاد یک تابع نموداری، از آن استفاده خواهیم کرد pearsonr() تابع SciPy برای انجام همبستگی و بررسی نتایج:
df_clean = df2.dropna()
df_clean('incomeperperson') = df_clean('incomeperperson').replace('', np.nan)
def plt_regression(x, y, data, label_1, label_2):
reg_plot = regplot(x=x, y=y, fit_reg=True, data=data)
plt.xlabel(label_1)
plt.ylabel(label_2)
plt.show()
plt_regression('lifeexpectancy', 'internetuserate', df_clean, 'Life Expectancy', 'Internet Use Rate')
plt_regression('employrate', 'internetuserate', df_clean, 'Employment Rate', 'Internet Use Rate')
print('Assoc. - life expectancy and internet use rate')
print(pearsonr(df_clean('lifeexpectancy'), df_clean('internetuserate')))
print('Assoc. - between employment rate and internet use rate')
print(pearsonr(df_clean('employrate'), df_clean('internetuserate')))
در اینجا خروجی ها آمده است:


Assoc. - life expectancy and internet use rate
(0.77081050888289, 5.983388253650836e-33)
Assoc. - between employment rate and internet use rate
(-0.1950109538173115, 0.013175901971555317)
اولین مقدار جهت و قدرت همبستگی است، در حالی که دومین مقدار P-value است. اعداد نشان میدهند که همبستگی نسبتاً قوی بین امید به زندگی و میزان استفاده از اینترنت وجود دارد که به دلیل شانس نیست. در همین حال، بین نرخ اشتغال و میزان استفاده از اینترنت همبستگی ضعیفتر، هرچند هنوز معنیدار وجود دارد.
توجه داشته باشید که امکان اجرای همبستگی پیرسون نیز وجود دارد روی داده های طبقه بندی شده، اگرچه نتایج تا حدودی متفاوت به نظر می رسد. اگر بخواهیم میتوانیم سطوح درآمد را گروهبندی کنیم و همبستگی پیرسون را اجرا کنیم روی آنها را می توانید از آن برای بررسی وجود متغیرهای تعدیل کننده که می توانند تأثیرگذار باشند استفاده کنید روی انجمن مورد علاقه شما
مدیران و تعامل آماری
بیایید روش محاسبه تعامل آماری بین چندین متغیر را بررسی کنیم، AKA moderation.
تعدیل زمانی است که یک متغیر سوم (یا بیشتر) بر قدرت ارتباط بین متغیر مستقل و متغیر وابسته تأثیر می گذارد.
روش های مختلفی برای تست وجود دارد اعتدال / تعامل آماری بین متغیر سوم و متغیرهای مستقل/وابسته. به عنوان مثال، اگر شما یک تست ANOVA انجام داده اید، می توانید با انجام یک تست ANOVA دو طرفه برای بررسی تعدیل احتمالی آن را تست کنید.
با این حال، یک روش قابل اعتماد برای تست تعدیل، صرف نظر از نوع آزمون آماری که اجرا کرده اید (ANOVA، Chi-Square، Pearson Correlation) این است که بررسی کنید آیا ارتباطی بین متغیرهای توضیحی و پاسخ برای هر زیرگروه/سطح سوم وجود دارد یا خیر. متغیر.
برای دقیقتر بودن، اگر آزمایشهای ANOVA را انجام میدادید، فقط میتوانید یک ANOVA را برای هر دسته در متغیر سوم اجرا کنید (متغیری که گمان میکنید ممکن است اثر تعدیلکننده داشته باشد. روی رابطه ای که در حال مطالعه آن هستید).
اگر از تست Chi-Square استفاده می کردید، فقط می توانید تست Chi-Square را انجام دهید روی فریم های داده جدید که تمام نقاط داده موجود در دسته های متغیر تعدیل کننده شما را در خود نگه می دارد.
اگر آزمون آماری شما همبستگی پیرسون است، باید برای متغیر تعدیل کننده دسته ها یا بن ها ایجاد کنید و سپس همبستگی پیرسون را برای هر سه آن بن ها اجرا کنید.
بیایید نگاهی گذرا به روش انجام همبستگی پیرسون برای تعدیل متغیرها بیندازیم. ما دستهها/سطوح مصنوعی را از ویژگیهای پیوسته خود ایجاد خواهیم کرد. این process برای تست اعتدال برای دو نوع تست دیگر (Chi-Square و ANOVA) بسیار شبیه است، اما در عوض شما متغیرهای طبقهبندی از قبل موجود را برای کار با آنها خواهید داشت.
ما می خواهیم یک متغیر مناسب را انتخاب کنیم تا به عنوان متغیر تعدیل کننده ما عمل کند. بیایید سطح درآمد را برای هر نفر امتحان کنیم و آن را به سه گروه مختلف تقسیم کنیم:
def income_groups(row):
if row('incomeperperson') <= 744.23:
return 1
elif row('incomeperperson') <= 942.32:
return 2
else:
return 3
df_clean('income_group') = df_clean.apply(lambda row: income_groups(row), axis=1)
subframe_1 = df_clean((df_clean('income_group') == 1))
subframe_2 = df_clean((df_clean('income_group') == 2))
subframe_3 = df_clean((df_clean('income_group') == 3))
print('Assoc. - life expectancy and internet use rate for low income countries')
print(pearsonr(subframe_1('lifeexpectancy'), subframe_1('internetuserate')))
print('Assoc. - life expectancy and internet use rate for medium income countries')
print(pearsonr(subframe_2('lifeexpectancy'), subframe_2('internetuserate')))
print('Assoc. - life expectancy and internet use rate for high income countries')
print(pearsonr(subframe_3('lifeexpectancy'), subframe_3('internetuserate')))
در اینجا خروجی ها آمده است:
Assoc. - life expectancy and internet use rate for low income countries
(0.38386370068495235, 0.010101223355274047)
Assoc. - life expectancy and internet use rate for medium income countries
(0.9966009508278395, 0.05250454954743393)
Assoc. - life expectancy and internet use rate for high income countries
(0.7019997488251704, 6.526819886007788e-18)
یک بار دیگر، اولین مقدار جهت و قدرت همبستگی است، در حالی که دومین مقدار P-value است.
نتیجه
statsmodels یک کتابخانه بسیار مفید است که به کاربران پایتون امکان تجزیه و تحلیل داده ها و اجرای تست های آماری را می دهد روی مجموعه داده ها میتوانید ANOVA، تستهای Chi-Square، همبستگی پیرسون و تستهایی را برای تعدیل انجام دهید.
هنگامی که با روش انجام این آزمون ها آشنا شدید، می توانید روابط معنادار بین متغیرهای وابسته و مستقل را آزمایش کنید و با ماهیت طبقه بندی یا پیوسته متغیرها سازگار شوید.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-17 03:15:05



