تخمین چگالی هسته در پایتون با استفاده از Scikit-Learn

معرفی

این مقاله مقدمه‌ای بر تخمین چگالی هسته با استفاده از کتابخانه یادگیری ماشین پایتون است. scikit-learn.

تخمین چگالی هسته (KDE) یک روش ناپارامتریک برای تخمین تابع چگالی احتمال یک متغیر تصادفی معین است. از آن با نام سنتی آن نیز یاد می شود پنجره Parzen-Rosenblatt روش، پس از کاشفان آن.

با توجه به نمونه‌ای از مشاهدات مستقل، توزیع شده یکسان (iid) \((x_1,x_2,\ldots,x_n)\) از یک متغیر تصادفی از یک توزیع منبع ناشناخته، تخمین چگالی هسته به صورت زیر ارائه می‌شود:

$$
p(x) = \frac{1}{nh} \Sigma_{j=1}^{n}K(\frac{x-x_j}{h})
$$

که در آن \(K(a)\) تابع هسته و \(h\) پارامتر هموارسازی است که پهنای باند نیز نامیده می شود. هسته‌های مختلف در ادامه این مقاله مورد بحث قرار می‌گیرند، اما فقط برای درک ریاضیات، اجازه دهید به یک مثال ساده نگاهی بیندازیم.

محاسبات مثال

فرض کنید نقاط نمونه را داریم (-2،-1،0،1،2)، با یک هسته خطی داده شده توسط: \(K(a)= 1-\frac{|a|}{h}\) و \(h=10\).

$$\begin{array}{lcccccccc}{\mathrm{ایکس}}_j& =& (& –2& –1& 0& 1& 2& )\\ |0–{\mathrm{ایکس}}_j|& =& (& 2& 1& 0& 1& 2& )\\ |\frac{0–{\mathrm{ایکس}}_j}{\mathrm{ساعت}}|& =& (& 0.2& 0.1& 0& 0.1& 0.2& )\\ ک(|\frac{0–{\mathrm{ایکس}}_j}{\mathrm{ساعت}}|)& =& (& 0.8& 0.9& 1& 0.9& 0.8& )\end{array}$$

موارد بالا را در فرمول \(p(x)\) وصل کنید:

$$
p(0) = \frac{1}{(5)(10)} (0.8+0.9+1+0.9+0.8) = 0.088
$$

تخمین چگالی هسته با استفاده از پایتون

در حالی که چندین روش برای محاسبه تخمین چگالی هسته در پایتون وجود دارد، ما از کتابخانه محبوب یادگیری ماشین استفاده خواهیم کرد. scikit-learn به این منظور. کتابخانه های زیر را در کد خود وارد کنید:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
from sklearn.model_selection import GridSearchCV

داده های مصنوعی

برای نشان دادن تخمین چگالی هسته، داده های مصنوعی از دو نوع مختلف توزیع تولید می شود. یکی توزیع لگ نرمال نامتقارن و دیگری توزیع گاوسی است. تابع زیر 2000 نقطه داده را برمی گرداند:

def generate_data(seed=17):
    
    rand = np.random.RandomState(seed)
    x = ()
    dat = rand.lognormal(0, 0.3, 1000)
    x = np.concatenate((x, dat))
    dat = rand.normal(3, 1, 1000)
    x = np.concatenate((x, dat))
    return x

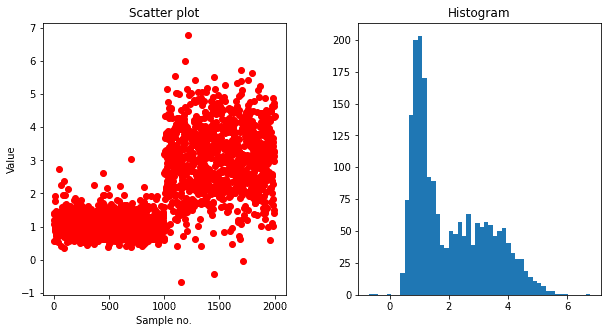
کد زیر نقاط را در آن ذخیره می کند x_train. می‌توانیم نمودار پراکندگی این نقاط را در امتداد محور y بسازیم یا می‌توانیم هیستوگرام این نقاط را ایجاد کنیم.

x_train = generate_data()(:, np.newaxis)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
plt.subplot(121)
plt.scatter(np.arange(len(x_train)), x_train, c='red')
plt.xlabel('Sample no.')
plt.ylabel('Value')
plt.title('Scatter plot')
plt.subplot(122)
plt.hist(x_train, bins=50)
plt.title('Histogram')
fig.subplots_adjust(wspace=.3)
plt.show()

استفاده از Scikit-Learn’s تراکم هسته

برای یافتن شکل تابع چگالی تخمین زده شده، می‌توان مجموعه‌ای از نقاط را با فاصله مساوی از یکدیگر تولید کرد و چگالی هسته را در هر نقطه تخمین زد. امتیاز آزمون توسط:

x_test = np.linspace(-1, 7, 2000)(:, np.newaxis)

حالا یک را ایجاد می کنیم KernelDensity شیء و استفاده کنید fit() روش برای یافتن امتیاز هر نمونه همانطور که در کد زیر نشان داده شده است. را KernelDensity() روش از دو پارامتر پیش فرض استفاده می کند kernel=gaussian و bandwidth=1.

model = KernelDensity()
model.fit(x_train)
log_dens = model.score_samples(x_test)

شکل توزیع را می توان با ترسیم امتیاز چگالی برای هر نقطه، به شرح زیر مشاهده کرد:

plt.fill(x_test, np.exp(log_dens), c='cyan')
plt.show()

آشنایی با پارامتر پهنای باند

مثال قبلی تخمین چشمگیری از تابع چگالی نیست که عمدتاً به پارامترهای پیش فرض نسبت داده می شود. بیایید با مقادیر مختلف پهنای باند آزمایش کنیم تا ببینیم چگونه بر تخمین چگالی تأثیر می گذارد.

bandwidths = (0.01, 0.05, 0.1, 0.5, 1, 4)
fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(10, 7))
plt_ind = np.arange(6) + 231

for b, ind in zip(bandwidths, plt_ind):
    kde_model = KernelDensity(kernel='gaussian', bandwidth=b)
    kde_model.fit(x_train)
    score = kde_model.score_samples(x_test)
    plt.subplot(ind)
    plt.fill(x_test, np.exp(score), c='cyan')
    plt.title("h="+str(b))

fig.subplots_adjust(hspace=0.5, wspace=.3)
plt.show()

ما به وضوح می توانیم ببینیم که افزایش پهنای باند منجر به تخمین صاف تری می شود. مقادیر پهنای باند بسیار کوچک منجر به منحنی‌های نوک تیز و لرزان می‌شود، در حالی که مقادیر بسیار بالا منجر به یک منحنی صاف بسیار تعمیم‌یافته می‌شوند که از دست می‌رود. روی جزئیات مهم انتخاب یک مقدار متعادل برای این پارامتر مهم است.

تنظیم پارامتر پهنای باند

را scikit-learn کتابخانه اجازه می دهد تا تنظیم bandwidth پارامتر از طریق اعتبارسنجی متقابل و مقدار پارامتری را برمی‌گرداند که احتمال ثبت داده‌ها را به حداکثر می‌رساند. تابعی که می توانیم برای رسیدن به این مورد استفاده کنیم این است GridSearchCV()، که به مقادیر متفاوتی نیاز دارد bandwidth پارامتر.

bandwidth = np.arange(0.05, 2, .05)
kde = KernelDensity(kernel='gaussian')
grid = GridSearchCV(kde, {'bandwidth': bandwidth})
grid.fit(x_train)

بهترین مدل را می توان با استفاده از best_estimator_ زمینه از GridSearchCV هدف – شی.

بیایید به تخمین بهینه تراکم هسته با استفاده از هسته گاوسی و print مقدار پهنای باند نیز:

kde = grid.best_estimator_
log_dens = kde.score_samples(x_test)
plt.fill(x_test, np.exp(log_dens), c='green')
plt.title('Optimal estimate with Gaussian kernel')
plt.show()
print("optimal bandwidth: " + "{:.2f}".format(kde.bandwidth))

optimal bandwidth: 0.15

اکنون، به نظر می رسد که این تخمین چگالی داده ها را به خوبی مدل می کند. نیمه اول نمودار با توزیع لگ نرمال مطابقت دارد و نیمه دوم نمودار توزیع نرمال را به خوبی مدل می کند.

هسته های مختلف برای تخمین چگالی

scikit-learn تخمین چگالی هسته را با استفاده از توابع مختلف هسته امکان پذیر می کند:

1. kernel ='cosine': \(K(a;h) \propto \cos (\frac{\pi a}{2h}) \text { if } |a|
2. kernel = 'epanechnikov': \(K(a;h) \propto 1 – \frac{a^2}{h^2}\)
3. kernel = 'exponential': \(K(a;h) \propto \exp (-\frac{|a|}{h})\)
4. kernel = 'gaussian': \(K(a;h) \propto \exp(-\frac{a^2}{2h^2})\)
5. kernel = 'linear': \(K(a;h) \propto 1 – \frac{|a|}{h} \text { if } |a|
6. kernel = 'tophat': \(K(a;h) \propto 1 \text { if } |a|

یک راه ساده برای درک روش کار این هسته ها ترسیم آنهاست. این به معنی ساختن یک مدل با استفاده از نمونه ای با یک مقدار، به عنوان مثال، 0 است. سپس، چگالی تمام نقاط را حول صفر تخمین بزنید و چگالی را در امتداد محور y رسم کنید. کد زیر کل را نشان می دهد process:

kernels = ('cosine', 'epanechnikov', 'exponential', 'gaussian', 'linear', 'tophat')
fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(10, 7))
plt_ind = np.arange(6) + 231

for k, ind in zip(kernels, plt_ind):
    kde_model = KernelDensity(kernel=k)
    kde_model.fit(((0)))
    score = kde_model.score_samples(np.arange(-2, 2, 0.1)(:, None))
    plt.subplot(ind)
    plt.fill(np.arange(-2, 2, 0.1)(:, None), np.exp(score), c='blue')
    plt.title(k)

fig.subplots_adjust(hspace=0.5, wspace=.3)
plt.show()

آزمایش با هسته های مختلف

بیایید با هسته های مختلف آزمایش کنیم و ببینیم چگونه آنها تابع چگالی احتمال را برای داده های مصنوعی ما تخمین می زنند.

ما میتوانیم استفاده کنیم GridSearchCV()، مانند قبل، برای یافتن بهینه bandwidth ارزش. با این حال، برای cosine، linear، و tophat هسته ها GridSearchCV() ممکن است به دلیل برخی امتیازات منجر به اخطار زمان اجرا شود -inf ارزش های. یکی از راه های ممکن برای رفع این مشکل، نوشتن یک تابع امتیازدهی سفارشی برای آن است GridSearchCV().

در کد زیر، -inf نمرات امتیازات آزمون در بخش حذف شده است my_scores() تابع امتیاز دهی سفارشی و یک مقدار میانگین برگردانده می شود. این لزوما بهترین طرح برای رسیدگی نیست -inf بسته به داده های مورد نظر، می توان مقادیر امتیاز و برخی استراتژی های دیگر را اتخاذ کرد.

def my_scores(estimator, X):
    scores = estimator.score_samples(X)
    
    scores = scores(scores != float('-inf'))
    
    return np.mean(scores)

kernels = ('cosine', 'epanechnikov', 'exponential', 'gaussian', 'linear', 'tophat')
fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(10, 7))
plt_ind = np.arange(6) + 231
h_vals = np.arange(0.05, 1, .1)

for k, ind in zip(kernels, plt_ind):
    grid = GridSearchCV(KernelDensity(kernel=k),
                        {'bandwidth': h_vals},
                        scoring=my_scores)
    grid.fit(x_train)
    kde = grid.best_estimator_
    log_dens = kde.score_samples(x_test)
    plt.subplot(ind)
    plt.fill(x_test, np.exp(log_dens), c='cyan')
    plt.title(k + " h=" + "{:.2f}".format(kde.bandwidth))

fig.subplots_adjust(hspace=.5, wspace=.3)
plt.show()

مدل نهایی بهینه شده

مثال بالا نشان می دهد که چگونه کرنل های مختلف چگالی را به روش های مختلف تخمین می زنند. یک مرحله نهایی راه اندازی است GridSearchCV() به طوری که نه تنها پهنای باند بهینه را کشف می کند، بلکه هسته بهینه را برای داده های مثال ما نیز کشف می کند. در اینجا کد نهایی است که تخمین چگالی نهایی و پارامترهای تنظیم شده آن را نیز در عنوان نمودار ترسیم می کند:

grid = GridSearchCV(KernelDensity(),
                    {'bandwidth': h_vals, 'kernel': kernels},
                    scoring=my_scores)
grid.fit(x_train)
best_kde = grid.best_estimator_
log_dens = best_kde.score_samples(x_test)
plt.fill(x_test, np.exp(log_dens), c='green')
plt.title("Best Kernel: " + best_kde.kernel+" h="+"{:.2f}".format(best_kde.bandwidth))
plt.show()

نتیجه

تخمین چگالی هسته با استفاده از scikit-learnکتابخانه sklearn.neighbors در این مقاله مورد بحث قرار گرفته است. مثال‌ها برای داده‌های تک متغیره ارائه شده‌اند، اما می‌توان آن را برای داده‌هایی با ابعاد چندگانه نیز اعمال کرد.

در حالی که یک روش شهودی و ساده برای تخمین چگالی برای توزیع های منبع ناشناخته است، یک دانشمند داده باید با احتیاط از آن استفاده کند زیرا نفرین ابعاد می تواند به طور قابل توجهی سرعت آن را کاهش دهد.