تغییر شکل تصویر در پایتون با Numpy، Pillow و OpenCV

در این مقاله من توضیح خواهم داد که اعمال یک تبدیل افین به یک تصویر چیست و چگونه آن را در پایتون انجام دهیم. ابتدا عملیات سطح پایین را نشان خواهم داد NumPy برای ارائه یک پیاده سازی هندسی دقیق. سپس آنها را در استفاده عملی تر از پایتون قرار می دهم بالش و OpenCV کتابخانه ها

این مقاله با استفاده از a نوشته شده است Jupyter notebook و منبع را می توان در سایت من یافت مخزن GitHub بنابراین، لطفا با خیال راحت آن را شبیه سازی کنید / فورک کنید و کد را آزمایش کنید.

تبدیل آفین چیست؟

مطابق با ویکیپدیا تبدیل افین یک نقشه برداری عملکردی بین دو فضای هندسی (آفین) است که نقاط، خطوط مستقیم و موازی و همچنین نسبت بین نقاط را حفظ می کند. تمام آن جمله بندی انتزاعی ریاضی یک تبدیل خطی ساده است که حداقل در زمینه پردازش تصویر منجر به یک یا چند دستکاری مانند چرخش، چرخش، مقیاس یا برش با اعمال یک ماتریس تبدیل می شود.

یک چیز خوب این است که از آنجایی که این اساساً یک عملیات هندسی دو بعدی است، می توانیم آن را تجسم کنیم. اجازه دهید با ارائه جدولی از تبدیل های وابسته که هر نوع دستکاری هندسی را توصیف می کند، شروع کنم.

نوع تبدیل	ماتریس تبدیل	معادله نقشه برداری پیکسل
هویت	$$ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$	$$x^{‘} = x$$ $$y^{‘} = y$$
مقیاس بندی	$$ \begin{bmatrix} c_{x} & 0 & 0 \\ 0 & c_{y} & 0 \\ 0 & 0 & 1 \end{bmatrix} $$	$$x^{‘} = c_{x} * x$$ $$y^{‘} = c_{y} * y$$
چرخش*	$$ \begin{bmatrix} cos \Theta & sin \Theta & 0 \\ -sin \Theta & cos \Theta & 0 \\ 0 & 0 & 1 \end{bmatrix} $$	$$x^{‘} = x * cos \Theta – y * sin \Theta$$ $$y^{‘} = x * cos \Theta + y * sin \Theta$$
ترجمه	$$ \begin{bmatrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{bmatrix} $$	$$x^{‘} = x + t_{x}$$ $$y^{‘} = y + t_{y}$$
برشی افقی	$$ \begin{bmatrix} 1 & s_{h} & ​​0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$	$$x^{‘} = x + s_{v} * y$$ $$y^{‘} = y$$
برش عمودی	$$ \begin{bmatrix} 1 & 0 & 0 \\ s_{v} & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$	$$x^{‘} = x$$ $$y^{‘} = x * s_{h} + y$$

• تبدیل آفین از زاویه چرخش در جهت عقربه‌های ساعت استفاده می‌کند که برخلاف دایره واحد هندسی معمولی زاویه‌ها است که در چرخش خلاف جهت عقربه‌های ساعت با صفر شروع از محور مثبت X اندازه‌گیری می‌شود، بنابراین خواهید دید که منفی زاویه اغلب اعمال می‌شود.

' علامت گذاری در اینجا فقط به مختصات خروجی تبدیل شده x یا y اشاره دارد نه نماد حساب برای یک مشتق

برای نشان دادن ساده، من چند تبدیل را برای دستکاری مختصات x و y نقاط زیر اعمال خواهم کرد که دارای مولفه های سه بعدی x، y و شاخص کاراکتر ASCII هستند، شبیه به روشی که یک پیکسل تصویر دارای مولفه های 3 بعدی x، y است. و فرکانس (یا شدت).

a = (0، 1، 0)
b = (1، 0، 1)
c = (0، -1، 2)
d = (-1، 0، 3)

دگرگونی های این مثال به صورت Scaling by 2 در تمام جهات و چرخش 90 درجه در جهت عقربه های ساعت خواهد بود. ابتدا تبدیل ها را به صورت جداگانه انجام می دهم تا تأثیر مستقیم هر کدام را نشان دهم روی نقاط را به اطراف حرکت می دهم، سپس تبدیل ها را ترکیب می کنم و آنها را در یک عمل اعمال می کنم.

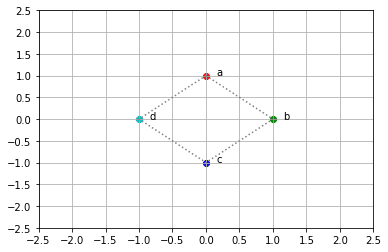
برای شروع می‌خواهم یک آرایه NumPy بسازم (بعضی‌ها ممکن است آن را ماتریس بخوانند) که هر سطر نشان‌دهنده نقطه‌ای است که ستون اول x، ستون دوم y و سومین شاخص حرف آن در مجموعه کاراکترهای ASCII است. مشابه جدول زیر بعد استفاده میکنم Matplotlib برای رسم نقاط (بعد از اعمال تبدیل هویت تغییرناپذیر) برای ارائه تصویری پایه از جایی که در آن ایستاده ایم.

نقطه	x (ردیف)	y (ستون)	شاخص آسکی
آ	0	1	0
ب	1	0	1
ج	0	-1	2
د	-1	0	3

import matplotlib.pyplot as plt
import numpy as np
import string


a, b, c, d = (0, 1, 0), (1, 0, 1), (0, -1, 2), (-1, 0, 3)


A = np.array((a, b, c, d))


I = np.eye(3)

color_lut = 'rgbc'
fig = plt.figure()
ax = plt.gca()
xs = ()
ys = ()
for row in A:
    output_row = I @ row
    x, y, i = output_row
    xs.append(x)
    ys.append(y)
    i = int(i) 
    c = color_lut(i)
    plt.scatter(x, y, color=c)
    plt.text(x + 0.15, y, f"{string.ascii_letters(i)}")
xs.append(xs(0))
ys.append(ys(0))
plt.plot(xs, ys, color="gray", linestyle='dotted')
ax.set_xticks(np.arange(-2.5, 3, 0.5))
ax.set_yticks(np.arange(-2.5, 3, 0.5))
plt.grid()
plt.show()

سه نقطه a، b و c رسم شده است روی یک شبکه پس از اعمال تبدیل Identity به آنها از طریق یک ماتریس برداری ساده حاصل ضرب نقطه ای آنها را بدون تغییر رها می کند.

اکنون حرکت خواهم کرد روی برای ایجاد یک ماتریس تغییر مقیاس \(T_s\) ، همانطور که در زیر نشان داده شده است، که قرارگیری نقاط را در همه جهات مقیاس می کند.

$$ T_s = \begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

حالا من حرکت خواهم کرد روی برای ترسیم نقاط تبدیل شده مشابه آنچه با نقاط اصلی بدون تغییر با تبدیل هویت انجام شد، اما، این بار ماتریس تبدیل مقیاس بندی تعریف شده در بالا را اعمال می کنم. برای تجسم بهتر، من یک خط نقطه چین را رسم می کنم که نقاط را به هم متصل می کند.

T_s = np.array(((2, 0, 0), (0, 2, 0), (0, 0, 1)))

fig = plt.figure()
ax = plt.gca()
xs_s = ()
ys_s = ()
for row in A:
    output_row = T_s @ row
    x, y, i = row
    x_s, y_s, i_s = output_row
    xs_s.append(x_s)
    ys_s.append(y_s)
    i, i_s = int(i), int(i_s) 
    c, c_s = color_lut(i), color_lut(i_s) 
    plt.scatter(x, y, color=c)
    plt.scatter(x_s, y_s, color=c_s)
    plt.text(x + 0.15, y, f"{string.ascii_letters(int(i))}")
    plt.text(x_s + 0.15, y_s, f"{string.ascii_letters(int(i_s))}'")

xs_s.append(xs_s(0))
ys_s.append(ys_s(0))
plt.plot(xs, ys, color="gray", linestyle='dotted')
plt.plot(xs_s, ys_s, color="gray", linestyle='dotted')
ax.set_xticks(np.arange(-2.5, 3, 0.5))
ax.set_yticks(np.arange(-2.5, 3, 0.5))
plt.grid()
plt.show()

از نمودار بالا باید بسیار واضح باشد که ابعاد x و y به سادگی با ضریب دو بزرگ‌تر شده‌اند در حالی که بعد سوم مسئول شاخص حروف ASCII بدون تغییر باقی مانده است. در واقع، کسانی که با جبر ماتریسی آشنا هستند متوجه خواهند شد که برای همه تبدیل‌های وابسته فهرست شده در جدول اول، مقدار نشان‌داده‌شده در بعد سوم همیشه بدون تغییر باقی می‌ماند، همانطور که با همه صفرها و یک مقدار تنها در شاخص بعد سوم نشان داده می‌شود. آخرین ستون

حالا اجازه دهید روش تفسیر تبدیل چرخش را توضیح دهم. من با حل دو تابع مثلثاتی برای زاویه چرخش مورد نظر 90 درجه شروع می کنم، سپس آنها را به سادگی به ماتریس تبدیل چرخش لیست شده در جدول قبلی متصل می کنم.

$$
گناه (90^{o}) = 1
$$

$$
cos (90^{o}) = 0
$$

$$ T_r = \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

اکنون تنها کاری که باید انجام دهم این است که همان منطق را برای تبدیل و رسم نقاط مانند زیر اعمال کنم:

T_r = np.array(((0, 1, 0), (-1, 0, 0), (0, 0, 1)))

fig = plt.figure()
ax = plt.gca()
for row in A:
    output_row = T_r @ row
    x_r, y_r, i_r = output_row
    i_r = int(i_r) 
    c_r = color_lut(i_r) 
    letter_r = string.ascii_letters(i_r)
    plt.scatter(x_r, y_r, color=c_r)
    plt.text(x_r + 0.15, y_r, f"{letter_r}'")

plt.plot(xs, ys, color="gray", linestyle='dotted')
ax.set_xticks(np.arange(-2.5, 3, 0.5))
ax.set_yticks(np.arange(-2.5, 3, 0.5))
plt.grid()
plt.show()

امیدواریم بتوانید از طرح متوجه شوید که تمام نقاط 90 درجه حول یک محور چرخش در مبدا چرخیده اند.

نکته دقیق در مورد تبدیل‌های affine که اساساً تبدیل‌های خطی هستند این است که می‌توانید تبدیل‌ها را ترکیب کرده و آنها را در یک مرحله اعمال کنید. برای نشان دادن این، من حاصل ضرب نقطه ای (ضرب ماتریس) دو ماتریس تبدیل خود را اعمال می کنم، مانند:

$$ T_{comb} = \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 2 & 0 & 0 \\ 0 و 2 و 0 \\ 0 و 0 و 1 \end{bmatrix} = \begin{bmatrix} 0 & 2 & 0 \\ -2 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

اکنون می توانم این ماتریس تبدیل ترکیبی را روی نقاط اعمال کنم و دوباره آنها را رسم کنم تا ترکیبی از مقیاس دو و چرخش 90 درجه را نشان دهم.

T = T_s @ T_r

fig = plt.figure()
ax = plt.gca()

xs_comb = ()
ys_comb = ()
for row in A:
    output_row = T @ row
    x, y, i = row
    x_comb, y_comb, i_comb = output_row
    xs_comb.append(x_comb)
    ys_comb.append(y_comb)
    i, i_comb = int(i), int(i_comb) 
    c, c_comb = color_lut(i), color_lut(i_comb) 
    letter, letter_comb = string.ascii_letters(i), string.ascii_letters(i_comb)
    plt.scatter(x, y, color=c)
    plt.scatter(x_comb, y_comb, color=c_comb)
    plt.text(x + 0.15 , y, f"{letter}")
    plt.text(x_comb + 0.15, y_comb, f"{letter_comb}'")
xs_comb.append(xs_comb(0))
ys_comb.append(ys_comb(0))
plt.plot(xs, ys, color="gray", linestyle='dotted')
plt.plot(xs_comb, ys_comb, color="gray", linestyle='dotted')
ax.set_xticks(np.arange(-2.5, 3, 0.5))
ax.set_yticks(np.arange(-2.5, 3, 0.5))
plt.grid()
plt.show()

کار با یک تصویر

تا به حال امیدوارم توانسته باشم شهودی در مورد روش استفاده از تبدیل های وابسته برای حرکت به سادگی در اطراف نقاط در فضای دوبعدی ایجاد کرده باشم، بنابراین می خواهم با برخی از داده های تصویر واقعی کار را شروع کنم. نمایش دقیق تری از روش عملکرد همه اینها ارائه دهید.

این همچنین به من اجازه می دهد تا موضوع مهم دیگری از تبدیل های وابسته را که به بعد سوم می پردازد، پوشش دهم. بعد سوم داده ها در یک تصویر نشان دهنده مقدار واقعی پیکسل است، یا گاهی اوقات به عنوان دامنه شدت به آن اشاره می شود، در حالی که مکان فیزیکی دو بعدی پیکسل ها در دو بعد دیگر به عنوان حوزه فضایی نامیده می شود.

برای شروع من یک تصویر را با استفاده از matplotlib می خوانم و نمایش می دهم که به سادگی یک حرف بزرگ بزرگ R است.

img = plt.imread('letterR.jpg')
img.shape 

با استفاده از imread(...) روشی که من می توانم در تصویر JPG بخوانم که نشان دهنده حرف بزرگ R در NumPy است ndarray. سپس ابعاد آرایه را که 1000 سطر در 1000 ستون است نمایش می دهم که با هم مکان های 1000000 پیکسلی را در حوزه فضایی تشکیل می دهند. سپس داده‌های پیکسل جداگانه به شکل آرایه‌ای از 4 عدد صحیح بدون علامت است که نشان‌دهنده یک کانال قرمز، سبز، آبی و آلفا (یا نمونه) است که با هم داده‌های شدت هر پیکسل را ارائه می‌کنند.

plt.figure(figsize=(5, 5))
plt.imshow(img)

در مرحله بعد، می‌خواهم مقیاس و چرخش قبلی را در حوزه فضایی داده‌های تصویر اعمال کنم، بنابراین مکان‌های پیکسل را مشابه آنچه قبلاً با داده‌های نقاط نشان دادم تغییر می‌دهد. با این حال، من باید رویکرد متفاوتی داشته باشم زیرا داده های تصویر به روشی متفاوت از ردیف های نقاط داده ای که قبلاً با آنها کار کردم سازماندهی شده اند. با داده‌های تصویر، باید شاخص‌های هر پیکسل از داده‌های ورودی را با استفاده از ماتریس تبدیل T، که قبلاً تعریف شد، به شاخص‌های خروجی تبدیل‌شده نگاشت کنم.

img_transformed = np.empty((2000, 2000, 4), dtype=np.uint8)
for i, row in enumerate(img):
    for j, col in enumerate(row):
        pixel_data = img(i, j, :)
        input_coords = np.array((i, j, 1))
        i_out, j_out, _ = T @ input_coords
        img_transformed(i_out, j_out, :) = pixel_data

plt.figure(figsize=(5, 5))
plt.imshow(img_transformed)

رسم تصویر پس از اعمال تبدیل به وضوح نشان می دهد که تصویر اصلی 90 درجه در جهت عقربه های ساعت چرخیده و 2X بزرگ شده است. با این حال، نتیجه اکنون به وضوح کاهش یافته است زیرا به راحتی می توانید ناپیوستگی در شدت پیکسل ها را مشاهده کنید.

برای درک دلیل این موضوع، دوباره از یک نمودار شبکه ساده برای نمایش استفاده می کنم. طرحی از 4 مربع را در یک شبکه 2×2 مشابه حوزه فضایی یک تصویر 2×2 در نظر بگیرید.

def plot_box(plt, x0, y0, txt, w=1, h=1):
    plt.scatter(x0, y0)
    plt.scatter(x0, y0 + h)
    plt.scatter(x0 + w, y0 + h)
    plt.scatter(x0 + w, y0)
    plt.plot((x0, x0, x0 + w, x0 + w, x0), (y0, y0 + h, y0 + h, y0, y0), color="gray", linestyle='dotted')
    plt.text(x0 + (.33 * w), y0 + (.5 * h), txt)


a = np.array((0,  1,  0))
b = np.array((1,  1,  1))
c = np.array((0,  0,  2))
d = np.array((1,  0,  3))

A = np.array((a, b, c, d))
fig = plt.figure()
ax = plt.gca()
for pt in A:
    x0, y0, i = I @ pt
    x0, y0, i = int(x0), int(y0), int(i)
    plot_box(plt, x0, y0, f"{string.ascii_letters(int(i))} ({x0}, {y0})")

ax.set_xticks(np.arange(-1, 5, 1))
ax.set_yticks(np.arange(-1, 5, 1))
plt.grid()
plt.show()

حالا ببینید چه اتفاقی می‌افتد وقتی یک تبدیل مقیاس‌بندی 2X را همانطور که در زیر نشان داده شده اعمال می‌کنم. به یاد بیاورید که:

$$ T_s = \begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

متوجه خواهید شد که چنین دگرگونی فضایی منجر به … خب، به بیان ساده، “شکاف” می شود، که من با ترسیم علامت های سوال همراه با مختصات آشکار کرده ام. شبکه 2×2 به یک شبکه 3×3 تبدیل می شود که مربع های اصلی بر اساس تغییر مکان می یابند. روی تبدیل خطی اعمال شده این بدان معنی است که (0,0) * \(T_s\) (0,0) به دلیل ویژگی‌های آن به عنوان یک بردار 0 باقی می‌ماند، اما بقیه با دو مقیاس می‌شوند، مانند (1,1) * \(T_s\) -> (2،2).

fig = plt.figure()
ax = plt.gca()
for pt in A:
    xt, yt, i = T_s @ pt
    xt, yt, i = int(xt), int(yt), int(i)
    plot_box(plt, xt, yt, f"{string.ascii_letters(i)}' ({xt}, {yt})")

delta_w, delta_h = 0.33, 0.5
plt.text(0 + delta_w, 1 + delta_h, "? (0, 1)")
plt.text(1 + delta_w, 0 + delta_h, "? (1, 0)")
plt.text(1 + delta_w, 1 + delta_h, "? (1, 1)")
plt.text(1 + delta_w, 2 + delta_h, "? (1, 2)")
plt.text(2 + delta_w, 1 + delta_h, "? (2, 1)")

ax.set_xticks(np.arange(-1, 5, 1))
ax.set_yticks(np.arange(-1, 5, 1))
plt.grid()
plt.show()

این سوال باقی می ماند که با آن شکاف هایی که معرفی شده اند چه باید کرد؟ یک فکر شهودی این است که به سادگی به تصویر اصلی برای پاسخ نگاه کنیم. اتفاقاً اگر معکوس تبدیل را به مختصاتی در خروجی اعمال کنیم، محل مربوط به ورودی اصلی را به دست می‌آورم.

در عملیات ماتریسی مانند نگاشت به عقب به صورت زیر است:

$$ (x, y, 1) = T_s^{-1} * (x’ y’ 1) $$

که در آن x’، y’ مختصات در شبکه 3×3 تبدیل شده فوق هستند، به طور خاص مکان گمشده، مانند (2، 1)، \(T_s^{-1}\) (مقادیر واقعی نشان داده شده در زیر) معکوس است ماتریس مقیاس 2x \(T_s\) و x, y مختصاتی هستند که در شبکه اصلی 2×2 یافت می شوند.

$$ T_s^{-1} = \begin{bmatrix} 1/2 & 0 & 0 \\ 0 & 1/2 & 0 \\ 0 & 0 & 1 \end{bmatrix}^{-1} $$

با این حال، به زودی متوجه خواهید شد که مشکلی وجود دارد که هنوز باید برطرف شود، زیرا هر یک از مختصات شکاف به مقادیر کسری سیستم مختصات 2×2 برمی گردد. در مورد داده های تصویر، شما واقعا نمی توانید کسری از پیکسل داشته باشید. این با مثالی از نگاشت شکاف (2، 1) به فضای اصلی 2×2 واضح تر خواهد بود، مانند:

$$ T_s^{-1} * (2، 1، 1) = (1، 1/2، 1) $$

در این حالت من y’ = 1/2 را به 0 گرد می کنم و می گویم که به (1, 0) نگاشت می شود. در مفهوم کلی، این روش انتخاب یک مقدار در شبکه اصلی 2×2 برای قرار دادن در شکاف های شبکه 3×3 تبدیل شده به عنوان درون یابی شناخته می شود، و در این مثال خاص من از یک نسخه ساده شده از روش درونیابی نزدیکترین همسایه استفاده می کنم.

خوب، حالا به داده های تصویر برگردیم. باید کاملاً واضح باشد که اکنون برای رفع این شکاف ها در نسخه مقیاس شده و چرخانده شده حرف R چه باید کرد. مختصات پیکسل در تصویر تبدیل شده برای یافتن مطابقت دقیق یا نزدیکترین همسایه در تصویر اصلی.

T_inv = np.linalg.inv(T)


def nearest_neighbors(i, j, M, T_inv):
    x_max, y_max = M.shape(0) - 1, M.shape(1) - 1
    x, y, _ = T_inv @ np.array((i, j, 1))
    if np.floor(x) == x and np.floor(y) == y:
        x, y = int(x), int(y)
        return M(x, y)
    if np.abs(np.floor(x) - x) < np.abs(np.ceil(x) - x):
        x = int(np.floor(x))
    else:
        x = int(np.ceil(x))
    if np.abs(np.floor(y) - y) < np.abs(np.ceil(y) - y):
        y = int(np.floor(y))
    else:
        y = int(np.ceil(y))
    if x > x_max:
        x = x_max
    if y > y_max:
        y = y_max
    return M(x, y,)

img_nn = np.empty((2000, 2000, 4), dtype=np.uint8)
for i, row in enumerate(img_transformed):
    for j, col in enumerate(row):
        img_nn(i, j, :) = nearest_neighbors(i, j, img, T_inv)

plt.figure(figsize=(5, 5))
plt.imshow(img_nn)

خیلی کثیف نیست درسته؟

باید توجه داشته باشم که در اکثر موارد روش نزدیکترین همسایه کافی نخواهد بود. دو روش متداول دیگر درون یابی وجود دارد که به نام های درون یابی دو خطی و دو مکعبی شناخته می شوند که به طور کلی نتایج بسیار بهتری ارائه می دهند. هنگام معرفی کتابخانه های Pillow و OpenCV در بخش های بعدی، در مورد این الگوریتم های درون یابی دیگر بیشتر صحبت خواهم کرد. هدف این بخش فقط ایجاد یک درک شهودی از روش کار کردن چیزها است.

تبدیل آفین با بالش

در این بخش به طور مختصر روش استفاده از کتابخانه پردازش تصویر عالی پایتون Pillow را برای انجام تبدیل‌های وابسته توضیح خواهم داد.

اول از همه، Pillow باید نصب شود. استفاده کردم pip برای انجام این کار، مانند این موارد:

$ pip install pillow

اکنون اولین قدم این است که import را Image کلاس از ماژول PIL (PIL نام ماژول پایتون مرتبط با Pillow است) و در تصویر من بخوانید.

from PIL import Image

برای خواندن در نام فایل تصویری نمونه letterR.jpg من روش کلاس را صدا می زنم Image.open(...)، با ارسال نام فایل به آن، که نمونه ای از فایل را برمی گرداند Image کلاس، که سپس آن را به یک آرایه numpy تبدیل می کنم و با matplotlib نمایش می دهم.

img = Image.open('letterR.jpg')
plt.figure(figsize=(5, 5))
plt.imshow(np.asarray(img))

بالشت Image کلاس یک متد مفید به نام دارد transform(...) که به شما امکان می‌دهد تبدیل‌های پیوندی ریزدانه را انجام دهید، اما چند مورد عجیب و غریب وجود دارد که قبل از اینکه به نمایش آن بپردازم، ابتدا باید در مورد آنها صحبت کنم. این transform(...) روش با نمایش دو پارامتر مورد نیاز آغاز می شود size به عنوان یک تاپل از ارتفاع و عرض، و به دنبال آن method از تبدیل اعمال خواهد شد، که خواهد بود Image.AFFINE در این مورد.

پارامترهای باقیمانده آرگومان های کلیدواژه اختیاری هستند که روش انجام تبدیل را کنترل می کنند. در مورد این مثال من از آن استفاده خواهم کرد data پارامتر، که دو ردیف اول یک ماتریس تبدیل افین را می گیرد.

به عنوان مثال، ماتریس تبدیل مقیاس 2 برابری که من با آن کار کرده‌ام که فقط به دو ردیف اول بریده شده است به این صورت است:

$$ T_s = \begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \end{bmatrix} $$

آخرین پارامتری که با آن استفاده خواهم کرد transform(...) روش است resample، که برای نشان دادن نوع الگوریتم درونیابی پیکسلی برای اعمال خارج از گزینه های ممکن استفاده می شود. Image.NEAREST (نزدیکترین همسایه)، Image.BILINEAR، یا Image.BICUBIC. این انتخاب اغلب بسته به آن متفاوت خواهد بود روی تحول در حال اعمال با این حال، دو خطی و دو مکعبی به طور کلی نتایج بهتری نسبت به نزدیکترین همسایه می دهند، اما همانطور که قبلاً در این مثال نشان داده شد نزدیکترین همسایه کاملاً خوب عمل می کند.

چند ویژگی وجود دارد که اولین باری که از آن استفاده کردم به عنوان یک گوچا واقعی برای من عمل کرد Image.transform(...) روش، به ویژه در مورد ساخت ماتریس تبدیل افین با ردیف آخر کوتاه شده است. بنابراین، من می‌خواهم مدتی را صرف بررسی این موضوع کنم که چرا کارها به همان شکل انجام می‌شوند، زیرا این کمی مشکل است process.

اولین چیزی که باید اتفاق بیفتد این است که تصویر باید طوری ترجمه شود که مبدا (0, 0) در وسط تصویر باشد. در مورد تصویر 1000 x 1000 حرف R در این مثال به معنای ترجمه 500- در x و y است.

در زیر ماتریس تبدیل عمومی ترجمه \(T_{translate}\) و ماتریس که در مثال \(T_{neg500}\) استفاده خواهم کرد را نشان می‌دهم.

$$ T_{translate} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} $$

$$
T_{neg500} = \begin{bmatrix}
1 و 0 و -500 \
0 و 1 و -500 \
0 و 0 و 1
\end{bmatrix}
$$

سپس ماتریس های 2X مقیاس \(T_{scale}\) و چرخش 90 درجه \(T_{rotate}\) از قبل وجود دارند. با این حال، کتابخانه Pillow در واقع تصمیم گرفت از زوایای هندسی استاندارد (یعنی در خلاف جهت عقربه‌های ساعت) به جای چرخش در جهت عقربه‌های ساعت که قبلاً توضیح دادم، استفاده کند. روی توابع گناه تلنگر. در زیر ماتریس های تبدیل فردی حاصل آمده است.

$$ T_{rotate} = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

$$
T_{scale} = \begin{bmatrix}
2 و 0 و 0 \
0 و 2 و 0 \
0 و 0 و 1
\end{bmatrix}
$$

در مرحله بعد، ماتریس ترجمه دیگری باید اعمال شود که برای تغییر مکان دامنه فضایی پیکسل ها عمل می کند و اساساً اولین موردی را که مبدا را در مرکز قرار داده است، نفی می کند. در این مورد، من به یک ترجمه مثبت 1000 در x و y نیاز دارم، که در آن 1000 از دو برابر نسخه اصلی می آید، زیرا آن را دو برابر کرده است.

$$ T_{pos1000} = \begin{bmatrix} 1 & 0 & 1000 \\ 0 & 1 & 1000 \\ 0 & 0 & 1 \end{bmatrix} $$

اینها مراحل تبدیل فردی مورد نیاز را تشکیل می‌دهند، بنابراین تنها چیزی که باقی می‌ماند ضرب کردن ماتریس‌ها به ترتیب (یعنی از راست به چپ) است، مانند زیر:

$$ T = T_{pos1000} * T_{rotate} * T_{scale} * T_{neg500} $$

خوب، پس در واقع آخرین مورد عجیب وجود دارد. این Image.transform(...) روش در واقع مستلزم آن است که معکوس ماتریس تبدیل به آن ارائه شود data پارامتر به عنوان یک آرایه مسطح (یا چند تایی) به استثنای آخرین ردیف.

$$ T_{inv} = T^{-1} $$

در کد این همه به صورت زیر کار می کند:

T_pos1000 = np.array((
    (1, 0, 1000),
    (0, 1, 1000),
    (0, 0, 1)))

T_rotate = np.array((
    (0, -1, 0),
    (1, 0, 0),
    (0, 0, 1)))

T_scale = np.array((
    (2, 0, 0),
    (0, 2, 0),
    (0, 0, 1)))

T_neg500 = np.array((
    (1, 0, -500),
    (0, 1, -500),
    (0, 0, 1)))
T = T_pos1000 @ T_rotate @ T_scale @ T_neg500
T_inv = np.linalg.inv(T)

img_transformed = img.transform((2000, 2000), Image.AFFINE, data=T_inv.flatten()(:6), resample=Image.NEAREST)
plt.imshow(np.asarray(img_transformed))

Affine Transformations با OpenCV2

ادامه دارد روی من مایلم به طور خلاصه روش انجام این دگرگونی های وابسته را با کتابخانه محبوب پردازش تصویر و بینایی کامپیوتری OpenCV شرح دهم. من در اینجا از کلمه مختصر استفاده می کنم زیرا تا حد زیادی همان چیزی است که در نمایش قبلی با استفاده از Pillow مورد نیاز است.

اول از همه، شما باید به این صورت نصب کنید:

$ pip install opencv-python

همانطور که در بالا ذکر کردم، همپوشانی قابل توجهی در روش شناسی بین رویکرد Pillow و استفاده از OpenCV وجود دارد. برای مثال، شما همچنان یک ماتریس تبدیل ایجاد می‌کنید که ابتدا آرایه پیکسل‌ها را روی مبدا متمرکز می‌کند و فقط از دو ردیف اول ماتریس تبدیل استفاده می‌کنید. تفاوت عمده این است که با OpenCV به جای ماتریس معکوس، ماتریس استاندارد را به آن می دهید.

بنابراین، با درک این موضوع، من وارد کد می‌شوم که با وارد کردن کد شروع می‌شود opencv-python ماژول که نامگذاری شده است cv2.

import cv2

خواندن تصویر به سادگی فراخوانی است cv2.imread(...) روش، ارسال نام فایل به عنوان آرگومان. این داده‌های تصویر را به شکل یک آرایه 3 بعدی numpy برمی‌گرداند، شبیه به روش عملکرد matplotlib، اما داده‌های پیکسل در بعد سوم از آرایه‌ای از کانال‌ها به ترتیب آبی، سبز، قرمز به جای قرمز، سبز تشکیل شده است. آبی، آلفا همانطور که در مورد خواندن با matplotlib بود.

بنابراین، برای رسم داده‌های تصویری ناچیز که از کتابخانه OpenCV نشات می‌گیرد، باید ترتیب کانال‌های پیکسل را معکوس کرد. خوشبختانه، OpenCV یک روش راحت ارائه می دهد cvtColor(...) همانطور که در زیر نشان داده شده است می توان از آن برای انجام این کار استفاده کرد (اگرچه افراد نابکار احتمالاً این را می دانند img(:,:,::-1) همین کار را خواهد کرد).

img = cv2.imread('letterR.jpg')
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))

چند مورد آخر که باید ذکر شود این است که OpenCV نیاز دارد که داده‌های موجود در ماتریس تبدیل از نوع شناور ۳۲ بیتی به جای شناور ۶۴ بیتی پیش‌فرض باشد، بنابراین مطمئن شوید که با استفاده از آن به ۳۲ بیت تبدیل کنید. numpy.float32(...). همچنین، API به cv2.warpAffine(...) توانایی تعیین نوع الگوریتم درونیابی پیکسلی را ارائه نمی دهد و من نتوانستم از روی اسناد تعیین کنم که چه چیزی استفاده می شود. اگر می دانید یا می دانید لطفا در نظرات زیر ارسال کنید.

T_opencv = np.float32(T.flatten()(:6).reshape(2,3))
img_transformed = cv2.warpAffine(img, T_opencv, (2000, 2000))
plt.imshow(cv2.cvtColor(img_transformed, cv2.COLOR_BGR2RGB))

نتیجه

در این مقاله من توضیح داده‌ام که تبدیل افین چیست و چگونه می‌توان آن را برای پردازش تصویر با استفاده از پایتون اعمال کرد. Numpy خالص و matplotlib برای ارائه یک توصیف بصری سطح پایین از روش عملکرد تبدیل‌های affine استفاده شد. من با نشان دادن اینکه چگونه می توان همین کار را با استفاده از دو کتابخانه محبوب پایتون Pillow و OpenCV به پایان رساند.

ممنون که خواندید و مثل همیشه از نظر دادن یا انتقاد در زیر خجالت نکشید.

منابع