درک OpenGL از طریق پایتون

معرفی

پیرو این مقاله توسط محمد جنید خالد، جایی که پایه OpenGL مفاهیم و تنظیمات توضیح داده شد، اکنون ما به دنبال چگونگی ساخت بیشتر خواهیم بود مجتمع اشیاء و چگونگی جان دادن آنها را

OpenGL بسیار قدیمی است و آموزش های زیادی را به صورت آنلاین پیدا نخواهید کرد روی چگونه می توان از آن به درستی استفاده کرد و آن را درک کرد زیرا تمام سگ های برتر در حال حاضر در فن آوری های جدید تا زانو عمیق هستند.

برای درک کد OpenGL مدرن، ابتدا باید آن را درک کنید کهن مفاهیمی که نوشته شد روی تبلت های سنگی توسط بازی سازان دانا مایان.

در این مقاله به چند موضوع اساسی که باید بدانید می پردازیم:

در بخش آخر، روش استفاده واقعی از OpenGL با کتابخانه های پایتون را بررسی خواهیم کرد PyGame و PyOpenGL.

در مقاله بعدی نگاهی عمیق تر به روش استفاده از OpenGL با پایتون و کتابخانه های ذکر شده در بالا خواهیم داشت.

عملیات ماتریس پایه

برای اینکه بتوانیم به درستی از بسیاری از توابع در OpenGL استفاده کنیم، به مقداری هندسه نیاز داریم.

تک تک نقطه در فضا را می توان با مختصات کارتزین. مختصات مکان هر نقطه معین را با تعریف آن نشان می دهد ایکس، Y و ز ارزش های.

ما عملاً از آنها استفاده خواهیم کرد ماتریس 1×3، یا بهتر است بگوییم 3 بعدی بردارها (بیشتر روی ماتریس بعد روی).

در اینجا نمونه هایی از مختصات آورده شده است:

$$\begin{gathered} آ=(5،3،4) \\ ب=(9،1،2) \end{gathered}$$

a و b نقاطی در فضا هستند، مختصات x آنها هستند 5 و 9 به ترتیب y بودن را مختصات می کند 3 و 1، و غیره روی.

در گرافیک کامپیوتری، اغلب، همگن مختصات به جای مختصات دکارتی معمولی قدیمی استفاده می شود. آنها اساساً یکسان هستند، فقط با یک پارامتر ابزار اضافی، که برای سادگی می گوییم همیشه 1.

بنابراین اگر مختصات منظم از a هستند (5,3,4)، مختصات همگن مربوطه خواهد بود (5,3,4,1). تئوری هندسی زیادی پشت این وجود دارد، اما برای این مقاله واقعاً ضروری نیست.

در مرحله بعد، یک ابزار ضروری برای نمایش تبدیلات هندسی هستند ماتریس ها. یک ماتریس اساسا یک آرایه دو بعدی است (در این مورد اندازه n*n، داشتن تعداد سطر و ستون برای آنها بسیار مهم است).

در حال حاضر عملیات ماتریسی، اغلب، بسیار ساده هستند، مانند جمع، تفریق، و غیره. اما مسلماً مهمترین عملیات باید پیچیده ترین عملیات باشد – ضرب. بیایید نگاهی به مثال های عملیات ماتریس اولیه بیندازیم:

$$\begin{gathered} آ=\left(\begin{array}{ccc}1& 2& 5\\ 6& 1& 9\\ 5& 5& 2\end{array}\right)–\text{ماتریس نمونه} \\ \left(\begin{array}{ccc}1& 2& 5\\ 6& 1& 9\\ 5& 5& 2\end{array}\right)+\left(\begin{array}{ccc}2& 5& 10\\ 12& 2& 18\\ 10& 10& 4\end{array}\right)=\left(\begin{array}{ccc}3& 7& 15\\ 18& 3& 27\\ 15& 15& 6\end{array}\right)–\text{اضافه کردن ماتریس} \\ \left(\begin{array}{ccc}2& 4& 10\\ 12& 2& 18\\ 10& 10& 4\end{array}\right)–\left(\begin{array}{ccc}1& 2& 5\\ 6& 1& 9\\ 5& 5& 2\end{array}\right)=\left(\begin{array}{ccc}1& 2& 5\\ 6& 1& 9\\ 5& 5& 2\end{array}\right)–\text{تفریق ماتریسی} \end{gathered}$$

اکنون، همانطور که تمام ریاضیات تمایل دارند انجام دهند، وقتی واقعاً چیزی عملی از آن بخواهید، نسبتاً پیچیده می شود.

فرمول ضرب ماتریس به شرح زیر است:

$$
c(i,j) = \sum_{k=1}^{n}a(i,k)*b(k,j)
$$

c به عنوان ماتریس حاصل، a و b ضرب و ضریب بودن.

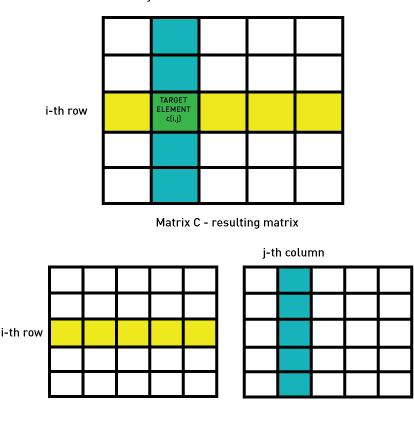
در واقع یک توضیح ساده برای این فرمول وجود دارد. هر عنصر را می توان با مجموع حاصلضرب تمام عناصر موجود در آن ساخت i– ردیف و jستون -ام. این دلیلی است که در a(i,k)، i ثابت است و k برای تکرار از طریق عناصر ردیف مربوطه استفاده می شود. همین اصل را می توان به کار برد b(k,j).

با دانستن این موضوع، یک شرط اضافی وجود دارد که باید برآورده شود تا بتوانیم از ضرب ماتریس استفاده کنیم. اگر بخواهیم ماتریس ها را ضرب کنیم A و B از ابعاد a*b و c*d. تعداد عناصر در یک ردیف در ماتریس اول (b) باید با تعداد عناصر یک ستون در ماتریس دوم یکسان باشد (c) تا بتوان از فرمول بالا به درستی استفاده کرد.

یک راه بسیار خوب برای تجسم این مفهوم، برجسته کردن سطرها و ستون‌هایی است که قرار است از عناصر آنها در ضرب برای یک عنصر معین استفاده شود. تصور کنید این دو برجسته شده اند خطوط بر روی یکدیگر، گویی در یک ماتریس هستند.

عنصری که آنها را رهگیری می کنند، موقعیت عنصر حاصل از جمع محصولات آنها است:

ضرب ماتریس بسیار مهم است زیرا اگر بخواهیم عبارت زیر را به زبان ساده توضیح دهیم: A*B (A و B ماتریس هستند)، می گوییم:

ما A را با استفاده از B تبدیل می کنیم.

به همین دلیل است که ضرب ماتریس ابزار اصلی برای تبدیل هر شی در OpenGL یا به طور کلی هندسه است.

آخرین چیزی که باید در مورد ضرب ماتریس بدانید این است که a دارد خنثی. این بدان معنی است که یک عنصر منحصر به فرد وجود دارد (ماتریس در این مورد) E که وقتی با هر عنصر دیگری ضرب شود A تغییر نمی کند Aمقدار، یعنی:

$$
(!\وجود{E}\ \ \برای همه{A})\ E*A=A
$$

علامت تعجب در رابطه با علامت وجود به این معنی است: یک عنصر منحصر به فرد E وجود دارد که …

در صورت ضرب با اعداد صحیح معمولی، E ارزش دارد 1. در مورد ماتریس ها، E دارای مقادیر زیر در حالت عادی است دکارتی (E₁) و مختصات همگن (E₂) به ترتیب:

$$E_1=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)E_2=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

هر تبدیل هندسی دارای ماتریس تبدیل منحصر به فرد خود است که دارای نوعی الگو است که مهمترین آنها عبارتند از:

• ترجمه
• مقیاس بندی
• انعکاس
• چرخش
• شییرینگ

ترجمه

ترجمه عمل حرکت به معنای واقعی کلمه توسط یک بردار مجموعه است. جسمی که تحت تأثیر دگرگونی قرار می گیرد به هیچ وجه شکل خود را تغییر نمی دهد و جهت خود را نیز تغییر نمی دهد – فقط در فضا حرکت می کند (به همین دلیل ترجمه به عنوان یک طبقه بندی می شود. جنبش دگرگونی).

ترجمه را می توان با فرم ماتریس زیر توصیف کرد:

$$\mathrm{تی}=\left(\begin{array}{cccc}1& 0& 0& {\mathrm{تی}}_{\mathrm{ایکس}}\\ 0& 1& 0& {\mathrm{تی}}_y\\ 0& 0& 1& {\mathrm{تی}}_z\\ 0& 0& 0& 1\end{array}\right)$$

این t-s نشان دهنده میزان شیء است x،y و z مقادیر مکان تغییر خواهد کرد.

بنابراین، پس از تبدیل هر مختصاتی با ماتریس ترجمه T، ما گرفتیم:

$$
(x,y,z)*T=(t_x+x,t_y+y,t_z+z)
$$

ترجمه با تابع OpenGL زیر اجرا می شود:

void glTranslatef(GLfloat tx, GLfloat ty, GLfloat tz);

همانطور که می بینید، اگر شکل ماتریس ترجمه را بدانیم، درک تابع OpenGL بسیار ساده است، این مورد در مورد همه تبدیل های OpenGL است.

اهمیت نده GLfloat، این فقط یک نوع داده هوشمندانه برای کار OpenGL است روی چندین پلتفرم، می توانید به این شکل نگاه کنید:

typedef float GLfloat;
typedef double GLdouble;
typedef someType GLsomeType;

این یک اقدام ضروری است زیرا همه سیستم ها فضای ذخیره سازی یکسانی برای a ندارند char، مثلا.

چرخش

چرخش تبدیل کمی پیچیده‌تر است، زیرا به این واقعیت ساده وابسته است روی 2 عامل:

• محور: حول چه خطی در فضای سه بعدی (یا نقطه ای در فضای دو بعدی) خواهیم چرخید
• میزان: چقدر (بر حسب درجه یا رادیان) در حال چرخش خواهیم بود

به همین دلیل، ابتدا باید چرخش را در فضای دو بعدی تعریف کنیم و برای آن به کمی مثلثات نیاز داریم.

در اینجا یک مرجع سریع وجود دارد:

این توابع مثلثاتی فقط در داخل مثلث قائم الزاویه قابل استفاده هستند (یکی از زوایا باید 90 درجه باشد).

ماتریس چرخش پایه برای چرخاندن یک جسم در فضای دوبعدی حول رأس (0,0) با زاویه A به شرح زیر می شود:

$$\left(\begin{array}{ccc}جoسآ& –س\mathrm{من}nآ& 0\\ س\mathrm{من}nآ& جoسآ& 0\\ 0& 0& 1\end{array}\right)$$

باز هم، سطر 3 و ستون 3 فقط در صورتی هستند که بخواهیم تبدیل‌های ترجمه را روی هم بگذاریم روی بالاتر از سایر تبدیل‌ها (که ما در OpenGL انجام می‌دهیم)، اگر به طور کامل درک نکنید که چرا آنها در حال حاضر آنجا هستند، مشکلی نیست. چیزها باید در مثال تبدیل ترکیبی روشن شوند.

همه اینها در فضای دو بعدی بود، حالا بیایید حرکت کنیم روی به فضای سه بعدی در فضای سه بعدی باید ماتریسی تعریف کنیم که بتواند یک شی را به دور خود بچرخاند هر خط

همانطور که یک مرد خردمند یک بار گفت: “ساده و احمقانه نگه دار!” خوشبختانه، شعبده بازان ریاضی برای یک بار آن را ساده و احمقانه نگه داشتند.

هر چرخش حول یک خط را می توان به چند تبدیل تقسیم کرد:

• چرخش حول محور x
• چرخش حول محور y
• چرخش حول محور z
• ترجمه های کاربردی (که بعداً به آنها پرداخته خواهد شد)

بنابراین، تنها سه چیزی که برای هر چرخش سه بعدی باید بسازیم، ماتریس هایی هستند که چرخش حول x، y، و z محور توسط یک زاویه A:

$${\mathrm{آر}}_{\mathrm{ایکس}}=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& جoسآ& –س\mathrm{من}nآ& 0\\ 0& س\mathrm{من}nآ& جoسآ& 0\\ 0& 0& 0& 1\end{array}\right){\mathrm{آر}}_y=\left(\begin{array}{cccc}جoسآ& 0& س\mathrm{من}nآ& 0\\ 0& 1& 0& 0\\ –س\mathrm{من}nآ& 0& جoسآ& 0\\ 0& 0& 0& 1\end{array}\right){\mathrm{آر}}_z=\left(\begin{array}{cccc}جoسآ& –س\mathrm{من}nآ& 0& 0\\ س\mathrm{من}nآ& جoسآ& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

چرخش سه بعدی با تابع OpenGL زیر اجرا می شود:

void glRotatef(GLfloat angle, GLfloat x, GLfloat y, GLfloat z);

• angle: زاویه چرخش بر حسب درجه (0-360)
• x,y,z: برداری که چرخش حول آن اجرا می شود

مقیاس بندی

مقیاس بندی عمل ضرب هر بعد شی هدف در a است اسکالر. این اسکالر می تواند باشد <1 اگر بخواهیم شی را کوچک کنیم، و می تواند باشد >1 اگر بخواهیم شی را بزرگ کنیم.

مقیاس بندی را می توان با فرم ماتریس زیر توصیف کرد:

$$\mathrm{اس}=\left(\begin{array}{cccc}{س}_{\mathrm{ایکس}}& 0& 0& 0\\ 0& {س}_y& 0& 0\\ 0& 0& {س}_z& 0\\ 0& 0& 0& 1\end{array}\right)$$

س_ایکس، س_y، س_z اسکالرهایی هستند که با عدد ضرب می شوند x، y، و z مقادیر شی مورد نظر

بعد از اینکه هر مختصاتی را با ماتریس مقیاس بندی تبدیل کردیم S ما گرفتیم:

$$(\mathrm{ایکس}،y،z)\ast \mathrm{اس}=({س}_{\mathrm{ایکس}}\ast \mathrm{ایکس}،{س}_y\ast y،{س}_z\ast z)$$

این تبدیل به ویژه هنگام مقیاس بندی یک شی بر اساس فاکتور مفید است ک (این بدان معناست که جسم حاصل دو برابر بزرگتر است)، این با تنظیم به دست می آید س_ایکس=س_y=س_z=ک:

$$(\mathrm{ایکس}،y،z)\ast \mathrm{اس}=({س}_{\mathrm{ایکس}}\ast \mathrm{ایکس}،{س}_y\ast y،{س}_z\ast z)$$

یک مورد خاص از پوسته پوسته شدن به عنوان شناخته شده است انعکاس. با تنظیم یا به دست می آید س_ایکس، س_y، یا س_z به -1. این فقط به این معنی است که ما علامت یکی از مختصات جسم را معکوس می کنیم.

به عبارت ساده تر، ما شی را قرار می دهیم روی طرف دیگر x، y، یا z محور.

این دگرگونی را می توان تغییر داد تا برای هر سطح بازتابی کار کند، اما در حال حاضر واقعاً به آن نیاز نداریم.

void glScalef(GLfloat sx, GLfloat sy, GLfloat sz);

تبدیل های مرکب

تبدیل های مرکب، تبدیل هایی هستند که از بیش از 1 تبدیل اساسی تشکیل شده اند (ذکر شده در بالا). تحولات A و B با ماتریس ضرب ماتریس های تبدیل مربوطه ترکیب می شوند M_a و M_b.

این ممکن است منطقی بسیار ساده به نظر برسد، با این حال مواردی وجود دارد که می تواند گیج کننده باشد. مثلا:

• ضرب ماتریس قابل تعویض نیست:

$$\begin{gathered} آ\ast ب\ne ب\ast آ \\ \text{A و B ماتریس هستند} \end{gathered}$$

• هر یک از این تبدیل ها یک تبدیل معکوس دارند. تبدیل معکوس تبدیلی است که تبدیل اصلی را خنثی می کند:

$$\begin{gathered} \mathrm{تی}=\left(\begin{array}{cccc}1& 0& 0& آ\\ 0& 1& 0& ب\\ 0& 0& 1& ج\\ 0& 0& 0& 1\end{array}\right){\mathrm{تی}}^{–1}=\left(\begin{array}{cccc}1& 0& 0& –آ\\ 0& 1& 0& –ب\\ 0& 0& 1& –ج\\ 0& 0& 0& 1\end{array}\right)E=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right) \\ \mathrm{تی}\ast {\mathrm{تی}}^{–1}=E \end{gathered}$$

• وقتی می خواهیم یک تبدیل مرکب را معکوس کنیم، باید ترتیب عناصر استفاده شده را تغییر دهیم:

$$(آ\ast ب\ast \mathrm{سی}{)}^{–1}={\mathrm{سی}}^{–1}\ast {ب}^{–1}\ast {آ}^{–1}$$

نکته این است که – ترتیب توپولوژیکی استفاده از ماتریس بسیار مهم است، درست مانند صعود به طبقه خاصی از یک ساختمان.

اگه تو هستی روی طبقه اول، و می خواهید به طبقه چهارم برسید، ابتدا باید به طبقه سوم و سپس به طبقه چهارم بروید.

اما اگر می خواهید به طبقه دوم برگردید، باید به طبقه سوم و سپس به طبقه دوم (به ترتیب توپولوژیک معکوس) بروید.

دگرگونی هایی که شامل یک نقطه ارجاع هستند

همانطور که قبلا ذکر شد، زمانی که یک تبدیل باید نسبت به یک نقطه خاص در فضا انجام شود، برای مثال چرخش حول یک نقطه ارجاع A=(a,b,c) در فضای سه بعدی، نه مبدا O=(0,0,0)، باید آن نقطه ارجاع را تغییر دهیم A به O با ترجمه همه چیز توسط T(-a,-b,-c).

سپس می‌توانیم هر تغییری را که باید انجام دهیم، انجام دهیم و وقتی کارمان تمام شد، همه چیز را دوباره ترجمه کنیم T(a,b,c)، به طوری که منشاء اصلی O دوباره مختصات را دارد (0,0,0).

شکل ماتریسی این مثال به صورت زیر است:

$$\mathrm{تی}\ast م\ast {\mathrm{تی}}^{–1}=\left(\begin{array}{cccc}1& 0& 0& –آ\\ 0& 1& 0& –ب\\ 0& 0& 1& –ج\\ 0& 0& 0& 1\end{array}\right)\ast م\ast \left(\begin{array}{cccc}1& 0& 0& آ\\ 0& 1& 0& ب\\ 0& 0& 1& ج\\ 0& 0& 0& 1\end{array}\right)$$

جایی که M تحولی است که ما می خواهیم انجام دهیم روی یک شی

نکته اصلی یادگیری این عملیات ماتریس این است که بتوانید به طور کامل درک کنید که OpenGL چگونه کار می کند.

نمایش مدلینگ

با وجود همه این موارد، بیایید نگاهی به یک نمایش مدل سازی ساده بیندازیم.

برای انجام هر کاری با OpenGL از طریق پایتون، از دو ماژول استفاده می کنیم – PyGame و PyOpenGL:

$ python3 -m pip install -U pygame --user
$ python3 -m pip install PyOpenGL PyOpenGL_accelerate

زیرا خالی کردن 3 کتاب تئوری گرافیک اضافی است روی خودتان، ما از کتابخانه PyGame استفاده خواهیم کرد. این اساسا فقط کوتاه خواهد شد process از مقداردهی اولیه پروژه گرفته تا مدل سازی و متحرک سازی واقعی.

برای شروع، ما نیاز داریم import همه چیز لازم از OpenGL و PyGame:

import pygame as pg
from pygame.locals import *

from OpenGL.GL import *
from OpenGL.GLU import *

در مثال زیر می بینیم که برای مدل سازی اشیاء غیر متعارف، تنها چیزی که باید بدانیم این است که چگونه شی پیچیده را می توان به قطعات کوچکتر و ساده تر تقسیم کرد.

از آنجایی که ما هنوز نمی دانیم برخی از این توابع چه کار می کنند، من برخی از تعاریف سطح سطح را در خود کد ارائه می دهم، فقط برای اینکه بتوانید ببینید چگونه می توان از OpenGL استفاده کرد. در مقاله بعدی، همه اینها به تفصیل پوشش داده خواهد شد – این فقط برای این است که یک ایده اولیه از روش کار با OpenGL به شما ارائه دهد:

def draw_gun():
    
    
    
    ambient_coeffsGray = (0.3, 0.3, 0.3, 1)
    diffuse_coeffsGray = (0.5, 0.5, 0.5, 1)
    specular_coeffsGray = (0, 0, 0, 1)
    glMaterialfv(GL_FRONT, GL_AMBIENT, ambient_coeffsGray)
    glMaterialfv(GL_FRONT, GL_DIFFUSE, diffuse_coeffsGray)
    glMaterialfv(GL_FRONT, GL_SPECULAR, specular_coeffsGray)
    glMateriali(GL_FRONT, GL_SHININESS, 1)

    
    
    
    
    
    
    
    glPushMatrix()

    glPushMatrix()
    glTranslatef(3.1, 0, 1.75)
    glRotatef(90, 0, 1, 0)
    glScalef(1, 1, 5)
    glScalef(0.2, 0.2, 0.2)
    glutSolidTorus(0.2, 1, 10, 10)
    glPopMatrix()

    glPushMatrix()
    glTranslatef(2.5, 0, 1.75)
    glScalef(0.1, 0.1, 1)
    glutSolidCube(1)
    glPopMatrix()

    glPushMatrix()
    glTranslatef(1, 0, 1)
    glRotatef(10, 0, 1, 0)
    glScalef(0.1, 0.1, 1)
    glutSolidCube(1)

    glPopMatrix()

    glPushMatrix()
    glTranslatef(0.8, 0, 0.8)
    glRotatef(90, 1, 0, 0)
    glScalef(0.5, 0.5, 0.5)
    glutSolidTorus(0.2, 1, 10, 10)
    glPopMatrix()

    glPushMatrix()
    glTranslatef(1, 0, 1.5)
    glRotatef(90, 0, 1, 0)
    glScalef(1, 1, 4)
    glutSolidCube(1)
    glPopMatrix()

    glPushMatrix()
    glRotatef(8, 0, 1, 0)
    glScalef(1.1, 0.8, 3)
    glutSolidCube(1)
    glPopMatrix()

    glPopMatrix()

def main():
    
    pg.init()
    
    glutInit(sys.argv)
    
    display = (800,600)
    pg.display.set_mode(display, DOUBLEBUF|OPENGL)
    glClearColor(0.1,0.1,0.1,0.3)
    gluPerspective(45, (display(0)/display(1)), 0.1, 50.0)
    gluLookAt(5,5,3,0,0,0,0,0,1)

    glTranslatef(0.0,0.0, -5)
    while True:
        
        for event in pg.event.get():
            if event.type == pg.QUIT:
                pg.quit()
                quit()

        
        glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT)
        
        draw_gun()
        
        
        pg.display.flip()
        pg.time.wait(10)

این دسته از کدها به ما نشان می دهد:

نتیجه

OpenGL بسیار قدیمی است و آموزش های زیادی را به صورت آنلاین پیدا نخواهید کرد روی چگونه می توان از آن به درستی استفاده کرد و آن را درک کرد زیرا تمام سگ های برتر در حال حاضر در فن آوری های جدید تا زانو عمیق هستند.

برای استفاده صحیح از OpenGL، نیاز به درک مفاهیم اولیه برای درک پیاده سازی ها از طریق توابع OpenGL است.

در این مقاله، عملیات اصلی ماتریس (ترجمه، چرخش، و مقیاس‌بندی) و همچنین تبدیل‌ها و تبدیل‌های ترکیبی که شامل یک نقطه ارجاع هستند را پوشش داده‌ایم.

در مقاله بعدی، ما استفاده خواهیم کرد PyGame و PyOpenGL برای مقداردهی اولیه یک پروژه، ترسیم اشیا، متحرک سازی آنها و غیره!