راهنمای قطعی خوشه بندی سلسله مراتبی با پایتون و Scikit-Learn

معرفی

در این راهنما تمرکز خواهیم کرد روی اجرای الگوریتم خوشه‌بندی سلسله مراتبی با Scikit-Learn برای حل یک مشکل بازاریابی

پس از خواندن راهنما متوجه خواهید شد:

• چه زمانی باید از خوشه بندی سلسله مراتبی استفاده کرد
• چگونه مجموعه داده را تجسم کنیم تا بفهمیم آیا برای خوشه بندی مناسب است یا خیر
• چگونه قبل ازprocess ویژگی ها و مهندسی ویژگی های جدید بر اساس روی مجموعه داده
• روش کاهش ابعاد مجموعه داده با استفاده از PCA
• روش استفاده و خواندن دندروگرام برای گروه های مجزا
• روش های مختلف پیوند و معیارهای فاصله اعمال شده برای دندروگرام ها و الگوریتم های خوشه بندی چیست؟
• استراتژی های خوشه بندی انباشته و تقسیمی چیست و چگونه کار می کنند
• روش پیاده‌سازی خوشه‌بندی سلسله مراتبی با Scikit-Learn
• متداول ترین مشکلات هنگام برخورد با الگوریتم های خوشه بندی چیست و چگونه آنها را حل کنیم

انگیزه

سناریویی را تصور کنید که در آن شما بخشی از یک تیم علم داده هستید که با بخش بازاریابی ارتباط برقرار می کند. بازاریابی مدتی است که داده‌های خرید مشتری را جمع‌آوری می‌کند و آنها می‌خواهند بر اساس آن را درک کنند روی داده های جمع آوری شده، در صورت وجود شباهت های بین مشتریان. این شباهت ها مشتریان را به گروه هایی تقسیم می کند و داشتن گروه های مشتری به هدف گذاری کمپین ها، تبلیغات، تبدیل ها و ایجاد روابط بهتر با مشتری کمک می کند.

آیا راهی وجود دارد که بتوانید در تعیین مشتریان مشابه کمک کنید؟ چند نفر از آنها متعلق به یک گروه هستند؟ و چند گروه مختلف وجود دارد؟

یکی از راه های پاسخ به این سوالات استفاده از الف است خوشه بندی الگوریتم‌هایی مانند K-Means، DBSCAN، Hierarchical Clustering و غیره. به‌طور کلی، الگوریتم‌های خوشه‌بندی شباهت‌هایی بین نقاط داده پیدا کرده و آنها را گروه‌بندی می‌کنند.

در این مورد، داده های بازاریابی ما نسبتاً کوچک است. ما اطلاعات داریم روی فقط 200 مشتری با توجه به تیم بازاریابی، مهم است که بتوانیم به وضوح برای آنها توضیح دهیم که چگونه تصمیمات بر اساس آن گرفته شده است روی تعداد خوشه ها، بنابراین به آنها توضیح می دهیم که چگونه الگوریتم واقعاً کار می کند.

از آنجایی که داده های ما کوچک است و توضیح پذیری یک عامل اصلی است، ما می توانیم اهرم استفاده کنیم خوشه بندی سلسله مراتبی برای حل این مسئله. این process نیز شناخته می شود تجزیه و تحلیل خوشه بندی سلسله مراتبی (HCA).

یکی از مزایای HCA این است که قابل تفسیر است و به خوبی کار می کند روی مجموعه داده های کوچک

نکته دیگری که در این سناریو باید مورد توجه قرار گیرد این است که HCA یک یک است نظارت نشده الگوریتم هنگام گروه‌بندی داده‌ها، ما راهی برای تأیید اینکه به درستی تشخیص می‌دهیم که یک کاربر به یک گروه خاص تعلق دارد، نداریم (گروه‌ها را نمی‌شناسیم). هیچ برچسبی وجود ندارد که بتوانیم نتایج خود را با آن مقایسه کنیم. اگر گروه ها را به درستی شناسایی کنیم، بعداً توسط بخش بازاریابی تأیید می شود روی به صورت روزانه (همانطور که با معیارهایی مانند ROI، نرخ تبدیل و غیره اندازه گیری می شود).

اکنون که مشکلی را که می‌خواهیم حل کنیم و روش حل آن را فهمیدیم، می‌توانیم نگاهی به داده‌های خود بیندازیم!

تجزیه و تحلیل داده های اکتشافی مختصر

پس از دانلود مجموعه داده، توجه کنید که a است CSV (مقادیر جدا شده با کاما) فایل فراخوانی شد shopping-data.csv. برای آسان‌تر کردن کاوش و دستکاری داده‌ها، آن‌ها را در a بارگذاری می‌کنیم DataFrame استفاده از پاندا:

import pandas as pd


path_to_file = 'home/projects/datasets/shopping-data.csv'
customer_data = pd.read_csv(path_to_file)

مارکتینگ گفت 200 سوابق مشتری را جمع آوری کرده است. ما می توانیم بررسی کنیم که آیا داده های بارگیری شده با 200 ردیف کامل است یا خیر shape صفت. به ما می گوید که به ترتیب چند سطر و ستون داریم:

customer_data.shape

این نتیجه در:

(200, 5)

عالی! داده های ما با 200 ردیف کامل است (سوابق مشتری) و همچنین 5 ستون داریم (امکانات). برای اینکه ببینیم بخش بازاریابی چه ویژگی هایی را از مشتریان جمع آوری کرده است، می توانیم نام ستون ها را با آن مشاهده کنیم columns صفت. برای انجام این کار، اجرا کنید:

customer_data.columns

اسکریپت بالا برمیگرده:

Index(('CustomerID', 'Genre', 'Age', 'Annual Income (k$)',
       'Spending Score (1-100)'),
      dtype='object')

در اینجا، ما می بینیم که بازاریابی ایجاد کرده است CustomerID، جمع آوری کرد Genre، Age، Annual Income (به هزار دلار) و الف Spending Score از 1 تا 100 برای هر 200 مشتری. وقتی برای توضیح خواسته شد، آنها گفتند که مقادیر موجود در Spending Score ستون نشان می دهد که یک فرد چند بار در یک مرکز خرید پول خرج می کند روی یک مقیاس از 1 تا 100. به عبارت دیگر، اگر یک مشتری نمره 0 داشته باشد، این شخص هرگز پول خرج نمی کند و اگر امتیاز 100 باشد، ما به تازگی بیشترین خرج کننده را تشخیص داده ایم.

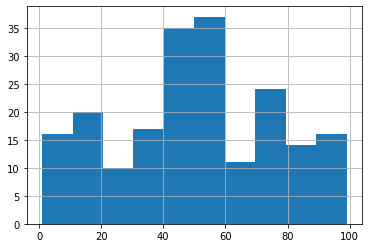
بیایید نگاهی گذرا به توزیع این امتیاز بیندازیم تا عادات خرج کردن کاربران در مجموعه داده خود را بررسی کنیم. پانداها آنجاست hist() روش کمک می کند:

customer_data('Spending Score (1-100)').hist()

با نگاهی به هیستوگرام می بینیم که بیش از 35 مشتری بین آنها امتیاز دارند 40 و 60، سپس کمتر از 25 امتیاز بین آنها وجود دارد 70 و 80. بنابراین اکثر مشتریان ما هستند مصرف کنندگان متعادلو پس از آن خرج کنندگان متوسط ​​تا زیاد. همچنین می توانیم ببینیم که یک خط بعد از آن وجود دارد 0، در سمت چپ توزیع، و یک خط دیگر قبل از 100، در سمت راست توزیع. این فضاهای خالی احتمالاً به این معنی است که توزیع شامل افراد غیر مصرف کننده نیست، که دارای امتیاز 0، و همچنین هیچ خرج کننده بالایی با امتیاز وجود ندارد 100.

برای بررسی درستی این موضوع، می‌توانیم به مقادیر حداقل و حداکثر توزیع نگاه کنیم. این مقادیر را می توان به راحتی به عنوان بخشی از آمار توصیفی یافت، بنابراین می توانیم از آن استفاده کنیم describe() روش برای درک سایر توزیع های مقادیر عددی:

customer_data.describe().transpose()

این جدولی به ما می دهد که از آنجا می توانیم توزیع مقادیر دیگر مجموعه داده خود را بخوانیم:

                         count 	mean 	std 		min 	25% 	50% 	75% 	max
CustomerID 				200.0 	100.50 	57.879185 	1.0 	50.75 	100.5 	150.25 	200.0
Age 					200.0 	38.85 	13.969007 	18.0 	28.75 	36.0 	49.00 	70.0
Annual Income (k$) 		200.0 	60.56 	26.264721 	15.0 	41.50 	61.5 	78.00 	137.0
Spending Score (1-100) 	200.0 	50.20 	25.823522 	1.0 	34.75 	50.0 	73.00 	99.0

فرضیه ما تایید می شود. را min ارزش از Spending Score است 1 و حداکثر است 99. پس نداریم 0 یا 100 امتیاز مصرف کنندگان بیایید سپس نگاهی به ستون های دیگر از انتقال بیاندازیم describe جدول. هنگام نگاه کردن به mean و std ستون ها، ما می توانیم آن را برای Age را mean است 38.85 و std تقریبا است 13.97. همین اتفاق برای Annual Income، با یک mean از 60.56 و std 26.26، و برای Spending Score با یک mean از 50 و std از 25.82. برای همه ویژگی ها، mean دور از انحراف معیار است که نشان می دهد داده های ما دارای تنوع بالایی هستند.

برای درک بهتر اینکه چگونه داده های ما تغییر می کند، اجازه دهید نمودار را ترسیم کنیم Annual Income توزیع:

customer_data('Annual Income (k$)').hist()

که به ما می دهد:

در هیستوگرام توجه کنید که بیشتر داده های ما، بیش از 35 مشتری، در نزدیکی تعداد متمرکز شده اند 60، روی ما mean، در محور افقی. اما وقتی به سمت انتهای توزیع حرکت می کنیم چه اتفاقی می افتد؟ وقتی به سمت چپ می رویم، از میانگین 60.560 دلار، مقدار بعدی که با آن مواجه می شویم 34.300 دلار است – میانگین (60.560 دلار) منهای تغییر استاندارد (26.260 دلار). اگر به سمت چپ توزیع داده‌های خود دورتر برویم، قانون مشابهی اعمال می‌شود، تغییر استاندارد (26.260 دلار) را از مقدار فعلی (34.300 دلار) کم می‌کنیم. بنابراین، با مقدار 8.040 دلار مواجه خواهیم شد. توجه کنید که چگونه داده های ما از 60 هزار دلار به سرعت به 8 هزار دلار رسید. هر بار 26.260 دلار “پرش” دارد – بسیار متفاوت است، و به همین دلیل است که ما چنین تنوع بالایی داریم.

تنوع و اندازه داده ها در تجزیه و تحلیل خوشه بندی مهم هستند زیرا اندازه گیری های فاصله بسیاری از الگوریتم های خوشه بندی به بزرگی داده ها حساس هستند. تفاوت در اندازه می‌تواند نتایج خوشه‌بندی را با نزدیک‌تر یا دورتر جلوه دادن یک نقطه به نقطه دیگر از آنچه که هست تغییر دهد و گروه‌بندی واقعی داده‌ها را مخدوش کند.

تاکنون، شکل داده های خود، برخی از توزیع های آن و آمار توصیفی را دیده ایم. با پانداها، ما همچنین می‌توانیم انواع داده‌های خود را فهرست کنیم و ببینیم که آیا همه 200 ردیف ما پر شده‌اند یا تعدادی دارند. null ارزش های:

customer_data.info()

این نتیجه در:

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 200 entries, 0 to 199
Data columns (total 5 columns):
 #   Column                  Non-Null Count  Dtype 
---  ------                  --------------  ----- 
 0   CustomerID              200 non-null    int64 
 1   Genre                   200 non-null    object
 2   Age                     200 non-null    int64 
 3   Annual Income (k$)      200 non-null    int64 
 4   Spending Score (1-100)  200 non-null    int64 
dtypes: int64(4), object(1)
memory usage: 7.9+ KB

در اینجا، می بینیم که هیچ وجود ندارد null مقادیر در داده ها و اینکه ما فقط یک ستون طبقه بندی داریم – Genre. در این مرحله، مهم است که در نظر داشته باشیم چه ویژگی هایی برای اضافه شدن به مدل خوشه بندی جالب به نظر می رسد. اگر بخواهیم ستون Genre را به مدل خود اضافه کنیم، باید مقادیر آن را از آن تغییر دهیم طبقه بندی شده به عددی.

بیایید ببینیم چگونه Genre با نگاهی سریع به 5 مقدار اول داده های ما پر می شود:

customer_data.head() 

این نتیجه در:

    CustomerID 	Genre 	Age 	Annual Income (k$) 	Spending Score (1-100)
0 	1 			Male 	19 		15 					39
1 	2 			Male 	21 		15 					81
2 	3 			Female 	20 		16 					6
3 	4 			Female 	23 		16 					77
4 	5 			Female 	31 		17 					40

به نظر می رسد که فقط دارد Female و Male دسته بندی ها. ما می توانیم با نگاهی به ارزش های منحصر به فرد آن مطمئن شویم unique:

customer_data('Genre').unique()

این فرض ما را تأیید می کند:

array(('Male', 'Female'), dtype=object)

اگر بخواهیم از این ویژگی استفاده کنیم، تا اینجا می دانیم که تنها دو ژانر داریم روی مدل ما Male می تواند تبدیل شود به 0 و Female به 1. همچنین مهم است که نسبت بین ژانرها را بررسی کنید تا ببینید آیا آنها متعادل هستند یا خیر. ما می توانیم این کار را با value_counts() روش و استدلال آن normalize=True برای نشان دادن درصد بین Male و Female:

customer_data('Genre').value_counts(normalize=True)

این خروجی:

Female    0.56
Male      0.44
Name: Genre, dtype: float64

ما 56 درصد از زنان در مجموعه داده ها و 44 درصد از مردان را داریم. تفاوت بین آنها فقط 16٪ است و داده های ما 50/50 نیست بلکه این است به اندازه کافی متعادل تا مشکلی ایجاد نشود اگر نتایج 70/30، 60/40 بود، ممکن است برای جمع‌آوری داده‌های بیشتر یا استفاده از نوعی تکنیک افزایش داده‌ها برای متعادل‌تر کردن این نسبت مورد نیاز باشد.

تا به حال، همه ویژگی ها اما Age، به اختصار مورد بررسی قرار گرفته است. در چه دغدغه هایی Age، معمولاً جالب است که آن را به سطل ها تقسیم کنیم تا بتوانیم مشتریان را بر اساس تقسیم بندی کنیم روی گروه های سنی آنها اگر این کار را انجام دهیم، باید رده های سنی را قبل از اضافه کردن آنها به مدل خود به یک عدد تبدیل کنیم. به این ترتیب، به جای استفاده از دسته بندی 15-20 سال، تعداد مشتریان را در این دسته حساب می کنیم 15-20 دسته، و آن عددی در ستون جدیدی به نام خواهد بود 15-20.

بعد از حدس زدن روی چه کاری می توان با هر دو دسته بندی انجام داد – یا طبقه بندی بودن – Genre و Age ستون، بیایید آنچه را که بحث شد اعمال کنیم.

رمزگذاری متغیرها و مهندسی ویژگی

بیایید با تقسیم کردن شروع کنیم Age به گروه هایی که در 10 تغییر می کنند، به طوری که ما 20-30، 30-40، 40-50، و غیره داریم. روی. از آنجایی که جوان‌ترین مشتری ما 15 سال دارد، می‌توانیم از 15 سالگی شروع کنیم و در 70 سالگی به پایان برسانیم، که سن پیرترین مشتری در داده‌ها است. با شروع از 15 و پایان دادن به 70، فواصل 15-20، 20-30، 30-40، 40-50، 50-60 و 60-70 را خواهیم داشت.

گروه کردن یا صندوقچه Age مقادیر را در این فواصل، می توانیم از پانداها استفاده کنیم cut() روشی برای برش آنها به سطل ها و سپس تخصیص بن ها به یک سطل جدید Age Groups ستون:

intervals = (15, 20, 30, 40, 50, 60, 70)
col = customer_data('Age')
customer_data('Age Groups') = pd.cut(x=col, bins=intervals)


customer_data('Age Groups') 

این نتیجه در:

0      (15, 20)
1      (20, 30)
2      (15, 20)
3      (20, 30)
4      (30, 40)
         ...   
195    (30, 40)
196    (40, 50)
197    (30, 40)
198    (30, 40)
199    (20, 30)
Name: Age Groups, Length: 200, dtype: category
Categories (6, interval(int64, right)): ((15, 20) < (20, 30) < (30, 40) < (40, 50) < (50, 60) < (60, 70))

توجه داشته باشید که هنگام نگاه کردن به مقادیر ستون، یک خط نیز وجود دارد که مشخص می کند 6 دسته داریم و تمام فواصل داده های binned را نمایش می دهد. به این ترتیب، ما داده های عددی قبلی خود را دسته بندی کرده و یک جدید ایجاد کرده ایم Age Groups ویژگی.

و در هر دسته چند مشتری داریم؟ با گروه بندی ستون و شمارش مقادیر با آن می توانیم به سرعت متوجه شویم groupby() و count():

customer_data.groupby('Age Groups')('Age Groups').count()

این نتیجه در:

Age Groups
(15, 20)    17
(20, 30)    45
(30, 40)    60
(40, 50)    38
(50, 60)    23
(60, 70)    17
Name: Age Groups, dtype: int64

به راحتی می توان تشخیص داد که اکثر مشتریان بین 30 تا 40 سال سن دارند و پس از آن مشتریان بین 20 تا 30 سال و سپس مشتریان بین 40 تا 50 سال قرار دارند. این نیز اطلاعات خوبی برای بخش بازاریابی است.

در حال حاضر، ما دو متغیر دسته بندی داریم، Age و Genre، که باید آن را به اعداد تبدیل کنیم تا بتوانیم در مدل خود استفاده کنیم. راه های مختلفی برای ایجاد این تغییر وجود دارد – ما از پانداها استفاده خواهیم کرد get_dummies() روشی که برای هر بازه و ژانر یک ستون جدید ایجاد می کند و سپس مقادیر آن را با 0 و 1 پر می کند – این نوع عملیات نامیده می شود. رمزگذاری تک داغ. بیایید ببینیم چگونه به نظر می رسد:

customer_data_oh = pd.get_dummies(customer_data)

customer_data_oh 

این یک پیش نمایش از جدول حاصل را به ما می دهد:

با خروجی، به راحتی می توان متوجه شد که ستون Genre به ستون ها تقسیم شد – Genre_Female و Genre_Male. وقتی مشتری زن است، Genre_Female برابر است با 1، و وقتی مشتری مرد باشد برابر است 0.

همچنین Age Groups ستون به 6 ستون تقسیم شد، یکی برای هر بازه، مانند Age Groups_(15, 20)، Age Groups_(20, 30)، و غیره روی. به همان صورت که Genre، زمانی که مشتری 18 ساله است، Age Groups_(15, 20) ارزش است 1 و ارزش تمام ستون های دیگر است 0.

را مزیت – فایده – سود – منفعت رمزگذاری تک داغ سادگی در نمایش مقادیر ستون است، درک آنچه اتفاق می افتد ساده است – در حالی که عیب این است که ما اکنون 8 ستون اضافی ایجاد کرده ایم تا با ستون هایی که قبلاً داشتیم جمع بندی کنیم.

رمزگذاری تک داغ همچنین 0 ها را به داده های ما اضافه می کند و آنها را پراکنده تر می کند، که می تواند برای برخی از الگوریتم هایی که به پراکندگی داده ها حساس هستند مشکل ساز باشد.

برای نیازهای خوشه‌بندی ما، به نظر می‌رسد رمزگذاری یک‌طرفه کار می‌کند. اما می‌توانیم داده‌ها را رسم کنیم تا ببینیم آیا واقعاً گروه‌های مجزایی برای خوشه‌بندی وجود دارد یا خیر.

پلات اساسی و کاهش ابعاد

مجموعه داده ما 11 ستون دارد و راه هایی وجود دارد که می توانیم آن داده ها را تجسم کنیم. اولین مورد با ترسیم آن در 10 بعدی است (موفق باشید). ده چون Customer_ID ستون در نظر گرفته نمی شود. مورد دوم با ترسیم ویژگی های عددی اولیه ما است، و سوم با تبدیل 10 ویژگی ما به 2 – بنابراین، انجام کاهش ابعاد.

ترسیم هر جفت داده

از آنجایی که ترسیم 10 بعد کمی غیرممکن است، ما رویکرد دوم را انتخاب می کنیم – ویژگی های اولیه خود را ترسیم می کنیم. ما می توانیم دو مورد از آنها را برای تجزیه و تحلیل خوشه بندی خود انتخاب کنیم. یکی از راه‌هایی که می‌توانیم همه جفت‌های داده خود را با هم ترکیب کنیم، Seaborn است pairplot():

import seaborn as sns


customer_data = customer_data.drop('CustomerID', axis=1)

sns.pairplot(customer_data)

که نمایش می دهد:

در یک نگاه، می‌توانیم نمودارهای پراکندگی را که به نظر می‌رسد دارای گروه‌هایی از داده‌ها هستند، تشخیص دهیم. یکی از مواردی که جالب به نظر می رسد، طرح پراکندگی است که ترکیب می شود Annual Income و Spending Score. توجه داشته باشید که هیچ جدایی واضحی بین سایر نمودارهای پراکندگی متغیر وجود ندارد. حداکثر، شاید بتوانیم بگوییم که دو غلظت مجزا از نقاط در آن وجود دارد Spending Score در مقابل Age طرح پراکنده.

هر دو قطعه پراکنده متشکل از Annual Income و Spending Score در اصل یکسان هستند. ما می توانیم آن را دو بار ببینیم زیرا محور x و y رد و بدل شده اند. با نگاهی به هر یک از آنها ، می توانیم ببینیم که پنج گروه مختلف به نظر می رسد. بیایید فقط این دو ویژگی را با Seaborn ترسیم کنیم scatterplot() برای نگاه دقیق تر:

sns.scatterplot(x=customer_data('Annual Income (k$)'),
                y=customer_data('Spending Score (1-100)'))

با نگاه دقیق تر، قطعاً می توانیم 5 گروه مختلف داده را تشخیص دهیم. به نظر می رسد مشتریان ما را می توان بر اساس خوشه بندی کرد روی چقدر آنها در یک سال و چقدر هزینه می کنند. این یکی دیگر از نکات مرتبط در تحلیل ما است. این مهم است که ما فقط دو ویژگی را در نظر بگیریم تا مشتریان خود را گروه بندی کنیم. اطلاعات دیگری که در مورد آنها داریم وارد معادله نمی شود. این به معنای تحلیل می دهد – اگر بدانیم مشتری چقدر درآمد و خرج می کند ، می توانیم به راحتی شباهت هایی را که لازم داریم پیدا کنیم.

عالیه! تاکنون ، ما در حال حاضر دو متغیر برای ساخت مدل خود داریم. علاوه بر آنچه این را نشان می دهد ، این مدل را نیز ساده تر ، پارسیمونی و قابل توضیح تر می کند.

رسم داده ها پس از استفاده از PCA

به نظر می رسد رویکرد دوم ما احتمالاً بهترین است ، اما بیایید نگاهی به رویکرد سوم خود بیندازیم. زمانی که نمی‌توانیم داده‌ها را ترسیم کنیم، زیرا ابعاد بسیار زیادی دارند، یا زمانی که غلظت داده‌ها یا جداسازی واضح در گروه‌ها وجود ندارد، می‌تواند مفید باشد. هنگامی که این شرایط رخ می دهد ، توصیه می شود با روشی به نام کاهش ابعاد داده را کاهش دهید تجزیه و تحلیل اجزای اصلی (PCA).

PCA ضمن تلاش برای حفظ هرچه بیشتر اطلاعات خود ، ابعاد داده های ما را کاهش می دهد. بیایید ابتدا ایده ای در مورد روش عملکرد PCA داشته باشیم و سپس می توانیم انتخاب کنیم که داده های خود را به چند بعد کاهش دهیم.

برای هر جفت ویژگی، PCA می بیند که آیا مقادیر بیشتر یک متغیر با مقادیر بیشتر متغیر دیگر مطابقت دارد یا خیر، و برای مقادیر کمتر نیز همین کار را انجام می دهد. بنابراین، اساساً محاسبه می کند که مقادیر ویژگی ها نسبت به یکدیگر چقدر متفاوت است – ما آن را آنها می نامیم کوواریانس. این نتایج سپس در یک ماتریس سازماندهی می شوند و به دست می آورند ماتریس کوواریانس.

پس از به دست آوردن ماتریس کوواریانس، PCA سعی می کند ترکیبی خطی از ویژگی هایی را پیدا کند که به بهترین وجه آن را توضیح می دهد – تا زمانی که مدلی را که توضیح می دهد شناسایی کند، با مدل های خطی مطابقت دارد. بیشترین مقدار واریانس.

با یافتن بهترین خط (ترکیب خطی)، PCA جهت محورهای خود را دریافت می کند که نامیده می شود بردارهای ویژهو ضرایب خطی آن، مقادیر ویژه. ترکیب بردارهای ویژه و مقادیر ویژه – یا جهت محورها و ضرایب – عبارتند از اجزای اصلی از PCA. و آن زمانی است که می توانیم تعداد ابعاد خود را بر اساس انتخاب کنیم روی واریانس توضیح داده شده هر ویژگی، با درک اینکه کدام مؤلفه های اصلی را می خواهیم بر اساس آن نگه داریم یا کنار بگذاریم روی چقدر واریانس را توضیح می دهند.

پس از به دست آوردن مؤلفه های اصلی، PCA از بردارهای ویژه برای تشکیل بردار ویژگی هایی استفاده می کند که داده ها را از محورهای اصلی به محورهایی که توسط مؤلفه های اصلی نشان داده شده اند تغییر جهت می دهد – به این ترتیب ابعاد داده کاهش می یابد.

قبل از اعمال PCA، باید از بین آن یکی را انتخاب کنیم Age ستون یا Age Groups ستون‌ها در داده‌های کدگذاری شده قبلی ما. از آنجایی که هر دو ستون اطلاعات یکسانی را نشان می دهند، معرفی دوبار آن بر واریانس داده ما تأثیر می گذارد. اگر Age Groups ستون انتخاب شده است، به سادگی آن را حذف کنید Age ستون با استفاده از پانداها drop() روش و دوباره آن را به customer_data_oh متغیر:

customer_data_oh = customer_data_oh.drop(('Age'), axis=1)
customer_data_oh.shape 

اکنون داده‌های ما 10 ستون دارند، به این معنی که می‌توانیم یک جزء اصلی را به ستون به‌دست آوریم و با اندازه‌گیری اینکه چقدر معرفی یک بعد جدید واریانس داده‌های ما را توضیح می‌دهد، انتخاب کنیم که چه تعداد از آنها استفاده کنیم.

بیایید این کار را با Scikit-Learn انجام دهیم PCA. ما واریانس توضیح داده شده هر بعد را محاسبه خواهیم کرد explained_variance_ratio_ ، و سپس به جمع تجمعی آنها نگاه کنید cumsum() :

from sklearn.decomposition import PCA

pca = PCA(n_components=10)
pca.fit_transform(customer_data_oh)
pca.explained_variance_ratio_.cumsum()

واریانس های توضیح داده شده تجمعی ما عبارتند از:

array((0.509337  , 0.99909504, 0.99946364, 0.99965506, 0.99977937,
       0.99986848, 0.99993716, 1.        , 1.        , 1.        ))

می بینیم که بعد اول 50٪ از داده ها را توضیح می دهد و وقتی با بعد دوم ترکیب می شوند، 99٪ درصد را توضیح می دهند. این بدان معنی است که 2 بعد اول 99٪ از داده های ما را توضیح می دهند. بنابراین می‌توانیم یک PCA با 2 مؤلفه اعمال کنیم، مؤلفه‌های اصلی خود را بدست آوریم و آنها را رسم کنیم:

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
pcs = pca.fit_transform(customer_data_oh)

pc1_values = pcs(:,0)
pc2_values = pcs(:,1)
sns.scatterplot(x=pc1_values, y=pc2_values)

نمودار داده بعد از PCA بسیار شبیه به نموداری است که فقط از دو ستون داده بدون PCA استفاده می کند. توجه داشته باشید که نقاطی که گروه‌ها را تشکیل می‌دهند، نزدیک‌تر هستند و بعد از PCA کمی متمرکزتر از قبل هستند.

تجسم ساختار سلسله مراتبی با دندروگرام

تا کنون، ما داده‌ها را بررسی کرده‌ایم، ستون‌های طبقه‌بندی کدگذاری شده یک‌طرفه، تصمیم گرفته‌ایم که کدام ستون‌ها برای خوشه‌بندی مناسب هستند و ابعاد داده را کاهش داده‌ایم. نمودارها نشان می دهد که ما 5 خوشه در داده های خود داریم، اما راه دیگری نیز برای تجسم روابط بین نقاط ما و کمک به تعیین تعداد خوشه ها وجود دارد – با ایجاد یک دندروگرام (معمولاً به عنوان “دندوگرام” اشتباه نوشته می شود). دندرو به معنای درخت به زبان لاتین

را دندروگرام نتیجه پیوند نقاط در یک مجموعه داده است. این یک نمایش بصری از خوشه بندی سلسله مراتبی است process. و چگونه خوشه بندی سلسله مراتبی process کار؟ خب… بستگی دارد – احتمالاً پاسخی است که قبلاً در Data Science زیاد شنیده اید.

آشنایی با خوشه بندی سلسله مراتبی

وقتی که الگوریتم خوشه بندی سلسله مراتبی (HCA) شروع به پیوند دادن نقاط و یافتن خوشه ها می کند، ابتدا می تواند نقاط را به 2 گروه بزرگ تقسیم کند و سپس هر یک از آن دو گروه را به 2 گروه کوچکتر تقسیم کند که در مجموع 4 گروه دارد که این تفرقه افکن و بالا پایین رویکرد.

از طرف دیگر، می‌تواند برعکس عمل کند – می‌تواند به تمام نقاط داده نگاه کند، 2 نقطه نزدیک‌تر به یکدیگر را پیدا کند، آنها را به هم پیوند دهد، و سپس نقاط دیگری را که نزدیک‌ترین آنها به آن نقاط مرتبط هستند بیابد و به ساختن 2 گروه ادامه دهد. از از پایین به بالا. که هست تجمعی رویکردی که ما توسعه خواهیم داد.

مراحل انجام خوشه بندی سلسله مراتبی تجمعی

برای اینکه رویکرد تجمعی حتی واضح شود، مراحلی از این وجود دارد خوشه بندی سلسله مراتبی تجمعی (AHC) الگوریتم:

1. در ابتدا، هر نقطه داده را به عنوان یک خوشه در نظر بگیرید. بنابراین، تعداد خوشه ها در ابتدا K خواهد بود – در حالی که K یک عدد صحیح است که تعداد نقاط داده را نشان می دهد.
2. با پیوستن به دو نزدیک ترین نقطه داده که منجر به خوشه های K-1 می شود، یک خوشه تشکیل دهید.
3. با پیوستن به دو نزدیکترین خوشه که منجر به خوشه های K-2 می شود، خوشه های بیشتری تشکیل دهید.
4. سه مرحله بالا را تکرار کنید تا یک خوشه بزرگ تشکیل شود.

اگر مراحل الگوریتم ACH را معکوس کنید، از 4 به 1 بروید – این مراحل به ** خوشه بندی سلسله مراتبی (DHC)**.

توجه داشته باشید که HCA ها می توانند تقسیم کننده و از بالا به پایین و یا تجمعی و از پایین به بالا باشند. رویکرد DHC از بالا به پایین زمانی بهترین کار می کند که خوشه های کمتر اما بزرگتر داشته باشید، بنابراین از نظر محاسباتی گران تر است. از سوی دیگر، رویکرد AHC از پایین به بالا برای زمانی که شما خوشه‌های کوچک‌تر زیادی دارید مناسب است. از نظر محاسباتی ساده‌تر، استفاده‌تر و در دسترس‌تر است.

بیایید دندروگرام داده های مشتری خود را ترسیم کنیم تا روابط سلسله مراتبی داده ها را به تصویر بکشیم. این بار ما از scipy کتابخانه برای ایجاد دندروگرام برای مجموعه داده ما:

import scipy.cluster.hierarchy as shc
import matplotlib.pyplot as plt

plt.figure(figsize=(10, 7))
plt.title("Customers Dendrogram")


selected_data = customer_data_oh.iloc(:, 1:3)
clusters = shc.linkage(selected_data, 
            method='ward', 
            metric="euclidean")
shc.dendrogram(Z=clusters)
plt.show()

خروجی اسکریپت به شکل زیر است:

در اسکریپت بالا، ما خوشه‌ها و زیرخوشه‌ها را با نقاط خود ایجاد کرده‌ایم، روش پیوند نقاطمان را تعریف کرده‌ایم (با اعمال ward روش)، و روش اندازه گیری فاصله بین نقاط (با استفاده از euclidean متریک).

با نمودار دندروگرام، فرآیندهای توصیف شده DHC و AHC را می توان مشاهده کرد. برای تجسم رویکرد از بالا به پایین، از بالای دندروگرام شروع کنید و به پایین بروید و برعکس آن را انجام دهید، از پایین شروع کنید و به سمت بالا حرکت کنید تا رویکرد پایین به بالا را تجسم کنید.

روشهای پیوند

بسیاری از روش های پیوند دیگر وجود دارد که با درک بیشتر در مورد روش کار آنها، می توانید روش مناسب را برای نیازهای خود انتخاب کنید. علاوه بر این، هر یک از آنها هنگام اعمال نتایج متفاوتی را به همراه خواهند داشت. در تجزیه و تحلیل خوشه‌بندی قانون ثابتی وجود ندارد، در صورت امکان، ماهیت مشکل را مطالعه کنید تا ببینید کدام یک به بهترین وجه مناسب است، روش‌های مختلف را آزمایش کنید و نتایج را بررسی کنید.

برخی از روش های پیوند عبارتند از:

• پیوند واحد: همچنین به آن گفته می شود نزدیکترین همسایه (NN). فاصله بین خوشه ها با فاصله بین نزدیکترین اعضای آنها تعریف می شود.

• پیوند کامل: همچنین به آن گفته می شود دورترین همسایه (FN)، دورترین الگوریتم نقطه، یا الگوریتم Voorhees. فاصله بین خوشه ها با فاصله بین دورترین اعضای آنها تعریف می شود. این روش از نظر محاسباتی گران است.

• پیوند متوسط: همچنین به عنوان شناخته می شود UPGMA (روش گروه زوج وزن نشده با میانگین حسابی)*. درصد تعداد نقاط هر خوشه با توجه به تعداد نقاط دو خوشه در صورت ادغام آنها محاسبه می شود.

• پیوند وزنی: همچنین به عنوان شناخته شده است WPGMA (روش گروه زوج وزنی با میانگین حسابی)*. نقاط مجزای دو خوشه به فاصله جمعی بین یک خوشه کوچکتر و یک خوشه بزرگتر کمک می کند.
• پیوند مرکز: همچنین به عنوان UPGMC (روش گروه زوج وزن نشده با استفاده از Centroids)*. برای هر خوشه یک نقطه تعریف شده با میانگین تمام نقاط (مرکز) محاسبه می شود و فاصله بین خوشه ها فاصله بین مرکز مربوطه آنها است.

• پیوند بخش: همچنین به عنوان شناخته شده است MISSQ (حداقل افزایش مجموع مربعات)*. این فاصله بین دو خوشه را مشخص می کند ، مجموع خطای مربع (ESS) را محاسبه می کند ، و پی در پی خوشه های بعدی را انتخاب می کند روی ESS کوچکتر. روش Ward به دنبال به حداقل رساندن افزایش ESS در هر مرحله است. بنابراین، به حداقل رساندن خطا.

متریک فاصله

علاوه بر پیوند، می‌توانیم برخی از پرکاربردترین معیارهای فاصله را نیز مشخص کنیم:

• اقلیدسی: همچنین به عنوان فیثاغورثی یا خط مستقیم فاصله فاصله بین دو نقطه در فضا را با اندازه گیری طول پاره خطی که بین آنها می گذرد محاسبه می کند. از قضیه فیثاغورث استفاده می کند و مقدار فاصله نتیجه است (c) از معادله:

$$
c^2 = a^2 + b^2
$$

• منهتن: همچنین به نام بلوک شهر، تاکسی فاصله این مجموع اختلافات مطلق بین اقدامات در تمام ابعاد دو نقطه است. اگر این ابعاد دو باشد ، ساخت راست و سپس در هنگام راه رفتن یک بلوک ، مشابه است.

• مینکوفسکی: این تعمیم هر دو مسافت اقلیدسی و منهتن است. این روشی است برای محاسبه فاصله بر اساس روی تفاوت های مطلق به ترتیب متریک Minkowski پ. اگر چه برای هر تعریف شده است p > 0، به ندرت برای مقادیر غیر از 1 ، 2 و ∞ (بی نهایت) استفاده می شود. فاصله مینکوفسکی همان فاصله منهتن است p=1، و همان فاصله اقلیدسی وقتی p=2.

$$
D \ Left (x ، y \ راست) = \ Left (\ sum_ {i = 1}^n | x_i-y_i |^p \ راست)^{\ frac {1} {p}}
$$

• چبیشف: همچنین به عنوان شناخته شده است صفحه شطرنج فاصله این حالت شدید فاصله مینکوفسکی است. وقتی از Infinity به عنوان مقدار پارامتر استفاده می کنیم p (p = ∞)، در نهایت با متریکی مواجه می شویم که فاصله را به عنوان حداکثر اختلاف مطلق بین مختصات تعریف می کند.
• کسینوس: فاصله کسینوس زاویه ای بین دو دنباله نقطه یا بردار است. شباهت کسینوس حاصل ضرب نقطه ای بردارها بر حاصلضرب طول آنها است.
• جاکارد: شباهت بین مجموعه های محدود نقاط را اندازه گیری می کند. به عنوان تعداد کل نقاط (کاردینالیته) در نقاط مشترک در هر مجموعه (تقاطع)، تقسیم بر تعداد کل نقاط (کاردینالیته) کل امتیازهای هر دو مجموعه (اتحاد) تعریف می شود.
• جنسن-شانون: مستقر روی واگرایی کولبک-لایبلر توزیع احتمال نقاط را در نظر می گیرد و شباهت بین آن توزیع ها را اندازه گیری می کند. این یک روش محبوب تئوری احتمال و آمار است.

ما انتخاب کردیم بخش و اقلیدسی برای دندروگرام زیرا آنها متداول ترین روش و متریک هستند. آنها معمولاً نتایج خوبی را ارائه می دهند زیرا Ward بر اساس نقاط پیوند می دهد روی به حداقل رساندن خطاها، و اقلیدسی در ابعاد پایین تر به خوبی کار می کند.

در این مثال، ما با دو ویژگی (ستون) از داده های بازاریابی و 200 مشاهده یا ردیف کار می کنیم. از آنجایی که تعداد مشاهدات بیشتر از تعداد ویژگی ها است (200 > 2)، ما در فضایی با ابعاد کم کار می کنیم.

هنگامی که تعداد ویژگی های (f) بزرگتر از تعداد مشاهدات است (N) – بیشتر به صورت نوشته شده است f >> N، یعنی یک داریم فضای با ابعاد بالا.

اگر بخواهیم ویژگی‌های بیشتری را وارد کنیم، بنابراین بیش از 200 ویژگی داریم، فاصله اقلیدسی ممکن است خیلی خوب کار نکند، زیرا در اندازه‌گیری تمام فواصل کوچک در یک فضای بسیار بزرگ که فقط بزرگ‌تر می‌شود، مشکل خواهد داشت. به عبارت دیگر، رویکرد فاصله اقلیدسی در کار با داده ها مشکل دارد پراکندگی. این موضوعی است که نام دارد نفرین ابعاد. مقادیر فاصله به قدری کوچک می‌شوند که گویی در فضای بزرگ‌تر «رقیق» می‌شوند و تا زمانی که به 0 تبدیل می‌شوند، تحریف می‌شوند.

ما قبلاً در مورد معیارها ، پیوندها و چگونگی هر یک از آنها می توانند بر نتایج ما تأثیر بگذارند. اکنون بیایید تجزیه و تحلیل دندروگرام را ادامه دهیم و ببینیم که چگونه می تواند نشانگر تعداد خوشه های موجود در مجموعه داده های ما باشد.

یافتن تعداد جالبی از خوشه ها در دندروگرام مانند یافتن بزرگترین فضای افقی است که هیچ خط عمودی ندارد (فضایی با طولانی ترین خطوط عمودی). این بدان معنی است که بین خوشه ها جدایی بیشتری وجود دارد.

ما می توانیم یک خط افقی که از طولانی ترین فاصله می گذرد رسم کنیم:

plt.figure(figsize=(10, 7))
plt.title("Customers Dendrogram with line")
clusters = shc.linkage(selected_data, 
            method='ward', 
            metric="euclidean")
shc.dendrogram(clusters)
plt.axhline(y = 125, color = 'r', linestyle = '-')

پس از یافتن خط افقی ، ما حساب می کنیم که چند بار خطوط عمودی ما توسط آن عبور کرده اند – در این مثال 5 بار. بنابراین 5 به نظر می رسد که نشانه خوبی از تعداد خوشه هایی است که بیشترین فاصله را بین آنها دارند.

اجرای خوشه بندی سلسله مراتبی آگلومراتیو

استفاده از داده های اصلی

تاکنون تعداد خوشه‌های پیشنهادی را برای مجموعه داده‌های خود محاسبه کرده‌ایم که با تحلیل اولیه و تجزیه و تحلیل PCA ما تأیید می‌کنند. اکنون می توانیم مدل خوشه بندی سلسله مراتبی تجمعی خود را با استفاده از Scikit-Learn ایجاد کنیم. AgglomerativeClustering و برچسب های نقاط بازاریابی را با labels_:

from sklearn.cluster import AgglomerativeClustering

clustering_model = AgglomerativeClustering(n_clusters=5, affinity='euclidean', linkage='ward')
clustering_model.fit(selected_data)
clustering_model.labels_

این نتیجه در:

array((4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3,
       4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 1,
       4, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 2, 0, 2, 0, 2,
       1, 2, 0, 2, 0, 2, 0, 2, 0, 2, 1, 2, 0, 2, 1, 2, 0, 2, 0, 2, 0, 2,
       0, 2, 0, 2, 0, 2, 1, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2,
       0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2,
       0, 2))

ما برای رسیدن به این نقطه بسیار تحقیق کرده ایم. و این برچسب ها به چه معناست؟ در اینجا، ما هر نقطه از داده های خود را به عنوان یک گروه از 0 تا 4 برچسب گذاری می کنیم:

data_labels = clustering_model.labels_
sns.scatterplot(x='Annual Income (k$)', 
                y='Spending Score (1-100)', 
                data=selected_data, 
                hue=data_labels,
                palette="rainbow").set_title('Labeled Customer Data')

این داده های نهایی “خوشه ای” ما است. شما می توانید نقاط داده با کد رنگی را در قالب پنج خوشه مشاهده کنید.

نقاط داده در پایین سمت راست (برچسب: 0، نقاط داده بنفش) متعلق به مشتریان با حقوق بالا اما هزینه کم است. اینها مشتریانی هستند که پول خود را با دقت خرج می کنند.

به طور مشابه، مشتریان در بالا سمت راست (برچسب: 2، نقاط داده سبز)، مشتریانی با حقوق بالا و هزینه های بالا هستند. اینها همان دسته از مشتریانی هستند که شرکت ها هدف آنها هستند.

مشتریان در وسط (برچسب: 1، نقاط داده آبی) آنهایی هستند که درآمد متوسط ​​و هزینه متوسط ​​دارند. بیشترین تعداد مشتریان متعلق به این دسته است. شرکت ها همچنین می توانند این مشتریان را با توجه به تعداد زیاد آنها هدف قرار دهند.

مشتریان پایین سمت چپ (برچسب: 4، قرمز) مشتریانی هستند که حقوق و خرج کم دارند و ممکن است با ارائه تبلیغات جذب شوند.

و در نهایت، مشتریان سمت چپ بالا (برچسب: 3، نقاط داده نارنجی) آنهایی هستند که درآمد بالا و هزینه کم دارند که به طور ایده آل هدف بازاریابی قرار می گیرند.

با استفاده از نتیجه PCA

اگر در سناریوی دیگری قرار داشتیم که در آن باید ابعاد داده ها را کاهش می دادیم. ما همچنین می‌توانیم به راحتی نتایج PCA «خوشه‌ای شده» را رسم کنیم. این کار را می توان با ایجاد یک مدل خوشه بندی تجمعی دیگر و به دست آوردن یک برچسب داده برای هر جزء اصلی انجام داد:

clustering_model_pca = AgglomerativeClustering(n_clusters=5, affinity='euclidean', linkage='ward')
clustering_model_pca.fit(pcs)

data_labels_pca = clustering_model_pca.labels_

sns.scatterplot(x=pc1_values, 
                y=pc2_values,
                hue=data_labels_pca,
                palette="rainbow").set_title('Labeled Customer Data Reduced with PCA')

توجه داشته باشید که هر دو نتیجه بسیار مشابه هستند. تفاوت اصلی این است که توضیح اولین نتیجه با داده های اصلی بسیار ساده تر است. واضح است که مشتریان را می توان بر اساس درآمد سالانه و امتیاز هزینه به پنج گروه تقسیم کرد. در حالی که، در رویکرد PCA، ما تمام ویژگی‌های خود را در نظر می‌گیریم، تا آنجا که می‌توانیم به واریانس توضیح داده شده توسط هر یک از آنها نگاه کنیم، درک این مفهوم دشوارتر است، به خصوص هنگام گزارش دادن به یک بخش بازاریابی.

هرچه حداقل باید داده هایمان را تغییر دهیم، بهتر است.

اگر یک مجموعه داده بسیار بزرگ و پیچیده دارید که در آن باید قبل از خوشه‌بندی کاهش ابعاد را انجام دهید – سعی کنید روابط خطی بین هر یک از ویژگی‌ها و باقیمانده‌های آنها را تجزیه و تحلیل کنید تا از استفاده از PCA نسخه پشتیبان تهیه کنید و قابلیت توضیح را افزایش دهید. process. با ساختن یک مدل خطی برای هر جفت ویژگی، می‌توانید روش تعامل ویژگی‌ها را درک کنید.

اگر حجم داده ها بسیار زیاد باشد، ترسیم جفت ویژگی ها، انتخاب نمونه ای از داده های خود، تا حد امکان متعادل و نزدیک به توزیع نرمال و انجام تجزیه و تحلیل غیرممکن می شود. روی ابتدا نمونه را درک کنید، آن را به دقت تنظیم کنید – و بعداً آن را در کل مجموعه داده اعمال کنید.

شما همیشه می توانید تکنیک های مختلف تجسم خوشه بندی را با توجه به ماهیت داده های خود (خطی، غیر خطی) انتخاب کنید و در صورت لزوم همه آنها را ترکیب یا آزمایش کنید.

نتیجه

تکنیک خوشه بندی در مورد داده های بدون برچسب می تواند بسیار مفید باشد. از آنجایی که بیشتر داده ها در دنیای واقعی بدون برچسب هستند و حاشیه نویسی داده ها هزینه بیشتری دارد، می توان از تکنیک های خوشه بندی برای برچسب گذاری داده های بدون برچسب استفاده کرد.

در این راهنما، ما یک مشکل واقعی علم داده را مطرح کرده‌ایم، زیرا تکنیک‌های خوشه‌بندی تا حد زیادی در تحلیل بازاریابی (و همچنین در تجزیه و تحلیل بیولوژیکی) استفاده می‌شوند. ما همچنین بسیاری از مراحل تحقیق برای رسیدن به یک مدل خوشه‌بندی سلسله مراتبی خوب و روش خواندن دندروگرام‌ها را توضیح داده‌ایم و در مورد اینکه آیا PCA یک مرحله ضروری است یا خیر، توضیح داده‌ایم. هدف اصلی ما این است که برخی از دام‌ها و سناریوهای مختلفی که در آنها می‌توانیم خوشه‌بندی سلسله مراتبی را پیدا کنیم، پوشش داده شوند.

خوشه بندی مبارک!