راهنمای قطعی رگرسیون لجستیک در پایتون

معرفی

گاهی اوقات با رگرسیون خطی توسط تازه کارها – به دلیل اشتراک گذاری این اصطلاح پسرفت – رگرسیون لجستیک بسیار متفاوت است رگرسیون خطی. در حالی که رگرسیون خطی مقادیری مانند 2، 2.45، 6.77 یا مقادیر پیوسته، ساختن آن a پسرفت الگوریتم، رگرسیون لجستیک مقادیری مانند 0 یا 1، 1 یا 2 یا 3 را پیش بینی می کند مقادیر گسسته، ساختن آن a طبقه بندی الگوریتم بله اسمش هست پسرفت اما یک است طبقه بندی الگوریتم بیشتر روی که در یک لحظه

بنابراین، اگر مشکل علم داده شما شامل مقادیر پیوسته باشد، می توانید a را اعمال کنید پسرفت الگوریتم (رگرسیون خطی یکی از آنهاست). در غیر این صورت، اگر شامل طبقه بندی ورودی ها، مقادیر گسسته یا کلاس ها باشد، می توانید یک طبقه بندی الگوریتم (رگرسیون لجستیک یکی از آنهاست).

در این راهنما، ما رگرسیون لجستیک را در پایتون با کتابخانه Scikit-Learn انجام خواهیم داد. همچنین دلیل این کلمه را توضیح خواهیم داد “پسرفت” در نام و روش عملکرد رگرسیون لجستیک وجود دارد.

برای انجام این کار، ابتدا داده هایی را بارگذاری می کنیم که طبقه بندی، تجسم و پیش پردازش می شوند. سپس، ما یک مدل رگرسیون لجستیک خواهیم ساخت که آن داده ها را درک می کند. سپس این مدل ارزیابی می شود و برای پیش بینی مقادیر بر اساس استفاده می شود روی ورودی جدید

انگیزه

شرکتی که شما در آن کار می کنید با یک مزرعه کشاورزی ترکیه مشارکت داشت. این مشارکت شامل فروش دانه کدو تنبل است. تخمه کدو تنبل برای تغذیه انسان بسیار مهم است. آنها حاوی نسبت خوبی از کربوهیدرات، چربی، پروتئین، کلسیم، پتاسیم، فسفر، منیزیم، آهن و روی هستند.

در تیم علم داده، وظیفه شما این است که تفاوت بین انواع تخم کدو را فقط با استفاده از داده ها تشخیص دهید – یا طبقه بندی داده ها بر اساس نوع بذر

مزرعه ترکیه با دو نوع تخم کدو کار می کند، یکی به نام چرچولیک و دیگری Ürgüp Sivrisi.

برای طبقه بندی دانه های کدو تنبل، تیم شما مقاله 2021 را دنبال کرده است “استفاده از روش های یادگیری ماشینی در طبقه بندی دانه های کدو تنبل (Cucurbita pepo L.). منابع ژنتیکی و تکامل محصول” از Koklu، Sarigil و Ozbek – در این مقاله، روشی برای عکاسی و استخراج اندازه‌گیری دانه‌ها از تصاویر وجود دارد.

پس از تکمیل process در مقاله شرح داده شده، اندازه گیری های زیر استخراج شد:

• حوزه – تعداد پیکسل های درون مرزهای یک دانه کدو تنبل
• محیط – دور یک دانه کدو تنبل بر حسب پیکسل
• طول محور اصلی – همچنین دور یک دانه کدو تنبل بر حسب پیکسل
• طول محور کوچک – فاصله محور کوچک یک دانه کدو تنبل
• عجیب و غریب – غیرمرکز بودن دانه کدو تنبل
• ناحیه محدب – تعداد پیکسل های کوچکترین پوسته محدب در ناحیه تشکیل شده توسط دانه کدو تنبل
• وسعت – نسبت سطح دانه کدو تنبل به پیکسل های جعبه مرزی
• قطر معادل – مربع root از ضرب مساحت دانه کدو تنبل در چهار تقسیم بر پی
• فشردگی – نسبت مساحت دانه کدو تنبل نسبت به مساحت دایره با محیط یکسان
• استحکام – حالت محدب و محدب دانه کدو تنبل
• گرد بودن – بیضی بودن تخم کدو بدون در نظر گرفتن اعوجاج لبه های آن
• نسبت تصویر – نسبت ابعاد دانه کدو تنبل

اینها اندازه گیری هایی هستند که باید با آنها کار کنید. علاوه بر اندازه گیری ها، همچنین وجود دارد کلاس برچسب برای دو نوع تخم کدو

برای شروع طبقه بندی دانه ها، اجازه دهید import داده و شروع به نگاه کردن به آن کنید.

شناخت مجموعه داده

پس از دانلود مجموعه داده، می‌توانیم آن را در یک ساختار دیتافریم با استفاده از pandas کتابخانه از آنجایی که این یک فایل اکسل است، از آن استفاده خواهیم کرد read_excel() روش:

import pandas as pd

fpath = 'dataset/pumpkin_seeds_dataset.xlsx' 
df = pd.read_excel(fpath)

هنگامی که داده ها بارگیری می شوند، می توانیم با استفاده از 5 ردیف اول نگاهی سریع بیندازیم head() روش:

df.head() 

این نتیجه در:

    Area 	Perimeter 	Major_Axis_Length 	Minor_Axis_Length 	Convex_Area 	Equiv_Diameter 	Eccentricity 	Solidity 	Extent 	Roundness 	Aspect_Ration 	Compactness 	Class
0 	56276 	888.242 	326.1485 			220.2388 			56831 			267.6805 		0.7376 			0.9902 		0.7453 	0.8963 		1.4809 			0.8207 			Çerçevelik
1 	76631 	1068.146 	417.1932 			234.2289 			77280 			312.3614 		0.8275 			0.9916 		0.7151 	0.8440 		1.7811 			0.7487 			Çerçevelik
2 	71623 	1082.987 	435.8328 			211.0457 			72663 			301.9822 		0.8749 			0.9857 		0.7400 	0.7674 		2.0651 			0.6929 			Çerçevelik
3 	66458 	992.051 	381.5638 			222.5322 			67118 			290.8899 		0.8123 			0.9902 		0.7396 	0.8486 		1.7146 			0.7624 			Çerçevelik
4 	66107 	998.146 	383.8883 			220.4545 			67117 			290.1207 		0.8187 			0.9850 		0.6752 	0.8338 		1.7413 			0.7557 			Çerçevelik

در اینجا، ما همه اندازه‌گیری‌ها را در ستون‌های مربوطه آن‌ها داریم امکانات، و همچنین کلاس ستون، ما هدف، که آخرین مورد در دیتافریم است. ما می توانیم با استفاده از تعداد اندازه گیری ها را ببینیم shape صفت:

df.shape 

خروجی این است:

(2500, 13)

نتیجه شکل به ما می گوید که 2500 ورودی (یا ردیف) در مجموعه داده و 13 ستون وجود دارد. از آنجایی که می دانیم یک ستون هدف وجود دارد – این بدان معنی است که ما 12 ستون ویژگی داریم.

اکنون می‌توانیم متغیر هدف، دانه کدو تنبل را بررسی کنیم Class. از آنجایی که ما آن متغیر را پیش بینی خواهیم کرد، جالب است که ببینیم چند نمونه از هر دانه کدو تنبل داریم. معمولاً هرچه تفاوت بین تعداد نمونه‌های کلاس‌های ما کمتر باشد، نمونه ما متعادل‌تر است و پیش‌بینی‌های ما بهتر است.

این بازرسی را می توان با شمارش هر نمونه بذر با عدد انجام داد value_counts() روش:

df('Class').value_counts() 

کد بالا نمایش می دهد:

Çerçevelik       1300
Ürgüp Sivrisi    1200
Name: Class, dtype: int64

می بینیم که 1300 نمونه از آن وجود دارد چرچولیک بذر و 1200 نمونه از Ürgüp Sivrisi دانه توجه داشته باشید که تفاوت بین آنها 100 نمونه است، تفاوت بسیار کمی که برای ما خوب است و نشان می دهد که نیازی به تعادل مجدد تعداد نمونه ها نیست.

بیایید به آمار توصیفی ویژگی‌های خود نیز نگاه کنیم describe() روشی برای مشاهده میزان توزیع خوب داده ها. ما همچنین جدول به دست آمده را با T برای آسان تر کردن مقایسه بین آمار:

df.describe().T

جدول حاصل این است:

                    count 	mean 			std 			min 		25% 			50% 			75% 			max
Area 				2500.0 	80658.220800 	13664.510228 	47939.0000 	70765.000000 	79076.00000 	89757.500000 	136574.0000
Perimeter 			2500.0 	1130.279015 	109.256418 		868.4850 	1048.829750 	1123.67200 		1203.340500 	1559.4500
Major_Axis_Length 	2500.0 	456.601840 		56.235704 		320.8446 	414.957850 		449.49660 		492.737650 		661.9113
Minor_Axis_Length 	2500.0 	225.794921 		23.297245 		152.1718 	211.245925 		224.70310 		240.672875 		305.8180
Convex_Area 		2500.0 	81508.084400 	13764.092788 	48366.0000 	71512.000000 	79872.00000 	90797.750000 	138384.0000
Equiv_Diameter 		2500.0 	319.334230 		26.891920 		247.0584 	300.167975 		317.30535 		338.057375 		417.0029
Eccentricity 		2500.0 	0.860879 		0.045167 		0.4921 		0.831700 		0.86370 		0.897025 		0.9481
Solidity 			2500.0 	0.989492 		0.003494 		0.9186 		0.988300 		0.99030 		0.991500 		0.9944
Extent 				2500.0 	0.693205 		0.060914 		0.4680 		0.658900 		0.71305 		0.740225 		0.8296
Roundness 			2500.0 	0.791533 		0.055924 		0.5546 		0.751900 		0.79775 		0.834325 		0.9396
Aspect_Ration 		2500.0 	2.041702 		0.315997 		1.1487 		1.801050 		1.98420 		2.262075 		3.1444
Compactness 		2500.0 	0.704121 		0.053067 		0.5608 		0.663475 		0.70770 		0.743500 		0.9049

با نگاه کردن به جدول، هنگام مقایسه منظور داشتن و انحراف معیار (std) ستون ها، مشاهده می شود که اکثر ویژگی ها میانگینی دارند که از انحراف معیار فاصله دارد. این نشان می دهد که مقادیر داده ها حول مقدار میانگین متمرکز نیستند، بلکه بیشتر در اطراف آن پراکنده هستند – به عبارت دیگر، آنها دارای تنوع بالا.

همچنین، هنگام نگاه کردن به کمترین (min) و بیشترین (max) ستون ها، برخی ویژگی ها، مانند Area، و Convex_Area، بین مقادیر حداقل و حداکثر تفاوت زیادی دارند. این بدان معنی است که آن ستون ها داده های بسیار کوچک و همچنین مقادیر داده های بسیار بزرگ یا دامنه بالاتر بین مقادیر داده

با تنوع بالا، دامنه بالا و ویژگی‌های با واحدهای اندازه‌گیری مختلف، بیشتر داده‌های ما از داشتن مقیاس یکسان برای همه ویژگی‌ها یا بودن بهره می‌برند. مقیاس شده. مقیاس داده ها داده ها را حول میانگین متمرکز می کند و واریانس آن را کاهش می دهد.

این سناریو احتمالاً همچنین نشان می دهد که مقادیر پرت و شدید در داده ها وجود دارد. بنابراین، بهتر است مقداری داشته باشید درمان پرت علاوه بر مقیاس بندی داده ها

برخی از الگوریتم های یادگیری ماشین وجود دارد، به عنوان مثال، الگوریتم های مبتنی بر درخت مانند طبقه بندی تصادفی جنگل، که تحت تأثیر واریانس داده های بالا، نقاط پرت و مقادیر شدید قرار نمی گیرند. رگرسیون لجستیک متفاوت است، مبتنی است روی تابعی که مقادیر ما را دسته بندی می کند و پارامترهای آن تابع می تواند تحت تاثیر مقادیری باشد که خارج از روند کلی داده ها هستند و واریانس بالایی دارند.

زمانی که رگرسیون لجستیک را پیاده سازی کنیم، کمی بیشتر در مورد رگرسیون لجستیک خواهیم فهمید. در حال حاضر، ما می توانیم به کاوش در داده های خود ادامه دهیم.

تجسم داده ها

تا به حال، با آمار توصیفی، ما یک عکس فوری انتزاعی از برخی از کیفیت داده ها داریم. گام مهم دیگر تجسم آن و تایید فرضیه ما در مورد واریانس بالا، دامنه و نقاط پرت است. برای اینکه ببینیم آیا آنچه تاکنون مشاهده کرده‌ایم در داده‌ها نشان داده می‌شود، می‌توانیم برخی نمودارها را رسم کنیم.

همچنین جالب است که ببینیم ویژگی ها چگونه به دو کلاسی که پیش بینی می شود مربوط می شود. برای انجام آن، اجازه دهید import را seaborn بسته بندی و استفاده کنید pairplot نمودار برای مشاهده هر توزیع ویژگی، و جداسازی هر کلاس در هر ویژگی:

import seaborn as sns


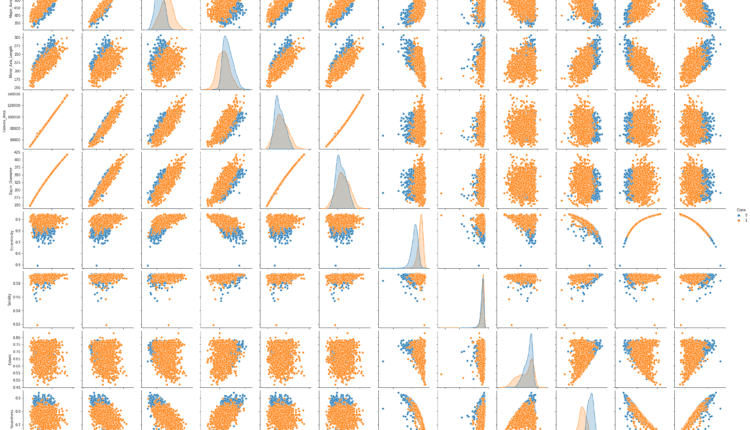
sns.pairplot(data=df, hue='Class')

با نگاهی به نمودار زوجی، می‌توانیم ببینیم که در بیشتر موارد نقاط Çerçevelik کلاس به وضوح از نقاط جدا شده است Ürgüp Sivrisi کلاس یا نقاط یک کلاس به سمت راست هستند، زمانی که بقیه در سمت چپ هستند، یا برخی از آنها بالا و بقیه پایین هستند. اگر بخواهیم از نوعی منحنی یا خط برای جدا کردن کلاس ها استفاده کنیم، این نشان می دهد که جدا کردن آنها آسان تر است، اگر آنها مخلوط می شدند، طبقه بندی کار سخت تری خواهد بود.

در Eccentricity، Compactness و Aspect_Ration ستون‌ها، برخی از نقاطی که “منزوی” هستند یا از روند کلی داده‌ها منحرف می‌شوند – نقاط پرت – نیز به راحتی قابل تشخیص هستند.

هنگام نگاه کردن به مورب از سمت چپ بالا به سمت راست پایین نمودار، توجه کنید که توزیع داده ها نیز مطابق با کلاس های ما دارای کد رنگی هستند. شکل‌های توزیع و فاصله بین هر دو منحنی، شاخص‌های دیگری از تفکیک پذیری آنها هستند – هر چه از یکدیگر دورتر باشند، بهتر است. در بیشتر موارد، آنها روی هم قرار نمی‌گیرند، که به این معنی است که جدا کردن آنها راحت‌تر است و همچنین به وظیفه ما کمک می‌کند.

به ترتیب، ما همچنین می‌توانیم باکس‌پلات‌های همه متغیرها را با علامت نشان دهیم sns.boxplot() روش. بیشتر مواقع، جهت دهی خطوط جعبه به صورت افقی مفید است، بنابراین اشکال جعبه‌ها مانند شکل‌های توزیع هستند، می‌توانیم این کار را با orient بحث و جدل:

sns.boxplot(data=df, orient='h') 

در طرح بالا به این نکته توجه کنید Area و Convex_Area در مقایسه با قدر ستون‌های دیگر، آنقدر بزرگی بالایی دارند که باکس‌پلات‌های دیگر را له می‌کنند. برای اینکه بتوانیم به تمام نمودارهای جعبه نگاه کنیم، می‌توانیم ویژگی‌ها را مقیاس‌بندی کنیم و دوباره آنها را رسم کنیم.

قبل از انجام این کار، بیایید فقط درک کنیم که اگر مقادیری از ویژگی‌ها وجود دارد که به‌عنوان مثال با مقادیر دیگر مرتبط هستند – اگر مقادیری وجود دارد که با بزرگ‌تر شدن سایر مقادیر ویژگی‌ها نیز بزرگ‌تر می‌شوند، داشتن یک همبستگی مثبت; یا اگر مقادیری برعکس هستند، کوچکتر می شوند در حالی که مقادیر دیگر کوچکتر می شوند، با داشتن a همبستگی منفی.

بررسی این موضوع مهم است زیرا داشتن روابط قوی در داده ها ممکن است به این معنی باشد که برخی از ستون ها از ستون های دیگر مشتق شده اند یا معنای مشابهی با مدل ما دارند. وقتی این اتفاق می افتد، نتایج مدل ممکن است بیش از حد برآورد شود و ما نتایجی را می خواهیم که به واقعیت نزدیکتر باشد. اگر همبستگی های قوی وجود داشته باشد، به این معنی است که می توانیم تعداد ویژگی ها را کاهش دهیم و از ستون های کمتری استفاده کنیم که مدل را بیشتر می کند. مختصر.

بیایید نگاهی به همبستگی های بین متغیرها بیندازیم و سپس می توانیم به پیش ازprocess داده. ما همبستگی ها را با corr() روش و آنها را با Seaborn تجسم کنید heatmap(). اندازه استاندارد نقشه حرارتی کوچک است، بنابراین ما این کار را خواهیم کرد import matplotlib (موتور/کتابخانه تجسم عمومی که Seaborn ساخته شده است روی top of) و اندازه را با figsize:

import matplotlib.pyplot as plt
plt.figure(figsize=(15, 10))

correlations = df.corr()
sns.heatmap(correlations, annot=True) 

در این نقشه حرارتی، مقادیر نزدیک به 1 یا -1 مقادیری هستند که باید به آنها توجه کنیم. مورد اول نشان دهنده همبستگی مثبت بالا و مورد دوم، همبستگی منفی بالا است. هر دو مقدار، اگر بالاتر از 0.8 یا 0.8- نباشد، برای مدل رگرسیون لجستیک ما مفید خواهد بود.

زمانی که همبستگی های بالایی مانند یکی از 0.99 بین Aspec_Ration و Compactness، این بدان معنی است که ما می توانیم فقط استفاده کنیم Aspec_Ration یا فقط Compactness، به جای هر دوی آنها (از آنجایی که تقریباً برابر هستند پیش بینی کننده ها از همدیگر). همین امر برای Eccentricity و Compactness با یک -0.98 همبستگی، برای Area و Perimeter با یک 0.94 همبستگی، و برخی از ستون های دیگر.

پیش پردازش داده ها

از آنجایی که قبلاً داده ها را برای مدتی کاوش کرده ایم، می توانیم پیش پردازش آن را شروع کنیم. در حال حاضر، بیایید از همه ویژگی ها برای پیش بینی کلاس استفاده کنیم. پس از به دست آوردن اولین مدل، یک خط مبنا، می‌توانیم برخی از ستون‌های بسیار همبسته را حذف کرده و آن را با خط مبنا مقایسه کنیم.

ستون های ویژگی ما خواهند بود X داده ها و ستون کلاس، ما y داده های هدف:

y = df('Class')
X = df.drop(columns=('Class'), axis=1)

تبدیل ویژگی‌های دسته‌بندی به ویژگی‌های عددی

در مورد ما Class ستون – مقادیر آن اعداد نیستند، این بدان معناست که ما نیز باید آنها را تبدیل کنیم. راه های زیادی برای انجام این تحول وجود دارد. در اینجا، ما از replace() روش و جایگزین کنید Çerçevelik به 0 و Ürgüp Sivrisi به 1.

y = y.replace('Çerçevelik', 0).replace('Ürgüp Sivrisi', 1)

نقشه برداری را در ذهن داشته باشید! هنگام خواندن نتایج مدل خود، می خواهید حداقل در ذهن خود آنها را دوباره به نام کلاس برای سایر کاربران تبدیل کنید.

تقسیم داده ها به مجموعه های قطار و تست

در کاوش خود، متوجه شدیم که ویژگی ها نیاز به مقیاس بندی دارند. اگر مقیاس را اکنون یا به صورت خودکار انجام دهیم، مقادیر را با کل مقیاس بندی می کنیم X و y. در این صورت معرفی می کنیم نشت داده، زیرا مقادیر مجموعه آزمایشی به زودی بر مقیاس بندی تأثیر می گذارد. نشت داده ها یکی از دلایل رایج نتایج غیرقابل تکرار و عملکرد بالای وهمی مدل های ML است.

فکر کردن در مورد مقیاس بندی نشان می دهد که ابتدا باید تقسیم شویم X و y داده ها را به مجموعه های آموزش و آزمایش و سپس به مناسب یک مقیاس کننده روی مجموعه آموزشی و به تبدیل هم مجموعه قطار و هم مجموعه تست (بدون اینکه مجموعه تست بر مقیاس کننده ای که این کار را انجام می دهد تأثیر بگذارد). برای این کار از Scikit-Learn استفاده خواهیم کرد train_test_split() روش:

from sklearn.model_selection import train_test_split
SEED = 42 

X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size=.25, 
                                                    random_state=SEED)

تنظیمات test_size=.25 این اطمینان حاصل می شود که ما از 25 درصد داده ها برای آزمایش و 75 درصد برای آموزش استفاده می کنیم. این می تواند حذف شود، زمانی که تقسیم پیش فرض باشد، اما پایتونیک روش نوشتن کد توصیه می کند که “صریح بودن بهتر از ضمنی” است.

پس از تقسیم داده ها به مجموعه های قطار و تست، بررسی تعداد رکوردها در هر مجموعه تمرین خوبی است. که می توان با shape صفت:

X_train.shape, X_test.shape, y_train.shape, y_test.shape

این نمایش می دهد:

((1875, 12), (625, 12), (1875,), (625,))

می بینیم که پس از تقسیم، 1875 رکورد برای آموزش و 625 رکورد برای تست داریم.

مقیاس بندی داده ها

هنگامی که مجموعه های قطار و آزمایش خود را آماده کردیم، می توانیم به مقیاس داده ها با Scikit-Learn ادامه دهیم. StandardScaler شی (یا مقیاس کننده های دیگر ارائه شده توسط کتابخانه). برای جلوگیری از نشتی، جرمگیر بر روی آن نصب شده است X_train سپس داده ها و مقادیر قطار برای مقیاس – یا تبدیل – هم قطار و هم داده آزمایش استفاده می شوند:

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

از آنجایی که معمولاً تماس می‌گیرید:

scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

دو خط اول را می توان با یک مفرد جمع کرد fit_transform() تماس، که متناسب با مقیاس کننده است روی مجموعه، و آن را در یک حرکت تبدیل می کند. اکنون می‌توانیم نمودارهای باکس پلات را بازتولید کنیم تا بعد از مقیاس‌بندی داده‌ها تفاوت را ببینیم.

با توجه به اینکه مقیاس بندی نام ستون ها را حذف می کند، قبل از ترسیم، می توانیم داده های قطار را در قالب داده با نام ستون ها دوباره سازماندهی کنیم تا تجسم را تسهیل کنیم:

column_names = df.columns(:12) 
X_train = pd.DataFrame(X_train, columns=column_names)

sns.boxplot(data=X_train, orient='h')

ما بالاخره می توانیم تمام جعبه های خود را ببینیم! توجه داشته باشید که همه آنها دارای نقاط پرت و ویژگی هایی هستند که توزیعی دورتر از نرمال دارند (که منحنی هایی به سمت چپ یا راست دارند) مانند Solidity، Extent، Aspect_Ration، و Compactness، همان هایی هستند که همبستگی بالاتری داشتند.

حذف نقاط پرت با روش IQR

ما قبلاً می دانیم که رگرسیون لجستیک می تواند تحت تأثیر عوامل پرت باشد. یکی از راه های درمان آنها استفاده از روشی به نام است محدوده بین چارکی یا IQR. مرحله اولیه روش IQR این است که داده‌های قطار خود را به چهار قسمت تقسیم می‌کنیم که به آن چارک می‌گویند. چارک اول، Q1، 25٪ از داده ها را تشکیل می دهد، دوم، Q2، به 50٪، سوم، Q3، به 75٪، و آخرین، Q4، تا 100% جعبه های موجود در باکس پلات با روش IQR تعریف می شوند و نمایشی بصری از آن هستند.

با در نظر گرفتن یک جعبه افقی، خط عمودی روی سمت چپ 25 درصد داده ها، خط عمودی در وسط، 50 درصد داده ها (یا میانه) و آخرین خط عمودی علامت گذاری می شود. روی سمت راست، 75 درصد از داده ها. هر چه اندازه هر دو مربعی که توسط خطوط عمودی تعریف شده‌اند یکنواخت‌تر باشند – یا خط عمودی وسط بیشتر باشد – به این معنی است که داده‌های ما به توزیع نرمال نزدیک‌تر هستند یا دارای انحراف کمتری هستند که برای تحلیل ما مفید است.

علاوه بر جعبه IQR، خطوط افقی نیز وجود دارد روی هر دو طرف آن این خطوط مقادیر حداقل و حداکثر توزیع تعریف شده توسط را مشخص می کنند

$$
حداقل = Q1 – 1.5 * IQR
$$

و

$$
حداکثر = Q3 + 1.5 * IQR
$$

IQR دقیقاً تفاوت بین Q3 و Q1 (یا Q3 – Q1) است و مرکزی ترین نقطه داده است. به همین دلیل است که هنگام یافتن IQR، در نهایت نقاط پرت را در انتهای داده یا در نقاط حداقل و حداکثر فیلتر می کنیم. نمودارهای جعبه ای به ما نگاهی اجمالی به ما می دهد که نتیجه روش IQR چه خواهد بود.

ما می توانیم از پاندا استفاده کنیم quantile() روش برای یافتن کمیت های ما، و iqr از scipy.stats بسته برای به دست آوردن محدوده داده بین ربعی برای هر ستون:

from scipy.stats import iqr

Q1 = X_train.quantile(q=.25)
Q3 = X_train.quantile(q=.75)

IQR = X_train.apply(iqr)

اکنون Q1، Q3 و IQR داریم، می‌توانیم مقادیر نزدیک‌تر به میانه را فیلتر کنیم:

minimum = X_train < (Q1-1.5*IQR)
maximum = X_train > (Q3+1.5*IQR)


filter = ~(minimum | maximum).any(axis=1)


X_train = X_train(filter)

پس از فیلتر کردن ردیف‌های آموزشی، می‌توانیم ببینیم که چه تعداد از آنها هنوز در داده‌ها هستند shape:

X_train.shape

این نتیجه در:

(1714, 12)

می بینیم که تعداد ردیف ها پس از فیلتر کردن از 1875 به 1714 رسید. این به این معنی است که 161 ردیف حاوی مقادیر پرت یا 8.5٪ از داده ها بودند.

پس از حذف نقاط پرت، تقریباً آماده هستیم تا داده ها را در مدل قرار دهیم. برای برازش مدل، از داده های قطار استفاده خواهیم کرد. X_train فیلتر شده است، اما چه؟ y_train?

y_train.shape

این خروجی:

(1875,)

توجه کنید که y_train هنوز 1875 ردیف دارد. ما باید تعداد را مطابقت دهیم y_train ردیف به تعداد X_train ردیف ها و نه فقط خودسرانه. ما باید مقادیر y نمونه‌هایی از دانه‌های کدو تنبل را که حذف کرده‌ایم، که احتمالاً در بین آنها پراکنده شده‌اند، حذف کنیم. y_train تنظیم. فیلتر شده X_train هنوز شاخص‌های اصلی خود را دارد و شاخص دارای شکاف‌هایی است که در آن نقاط پرت را حذف کردیم! سپس می توانیم از ایندکس استفاده کنیم X_train DataFrame برای جستجوی مقادیر مربوطه در y_train:

y_train = y_train.iloc(X_train.index)

پس از انجام این کار، می توانیم به آن نگاه کنیم y_train دوباره شکل دهید:

y_train.shape

کدام خروجی ها:

(1714,)

اکنون، y_train همچنین دارای 1714 ردیف است و آنها مشابه هستند X_train ردیف ها ما بالاخره آماده ایم مدل رگرسیون لجستیک خود را ایجاد کنیم!

اجرای مدل رگرسیون لجستیک

قسمت سخت تمام شد! زمانی که صحبت از استفاده از کتابخانه‌هایی مانند Scikit-Learn می‌شود، که کاربرد مدل‌های ML را در چند خط ساده‌تر کرده است، معمولاً پیش‌پردازش دشوارتر از توسعه مدل است.

اول ما import را LogisticRegression کلاس و نمونه سازی آن، ایجاد یک LogisticRegression هدف – شی:

from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(random_state=SEED)

دوم، ما داده های قطار خود را با logreg مدل با fit() روش، و پیش بینی داده های تست ما با استفاده از predict() روش، ذخیره نتایج به عنوان y_pred:

logreg.fit(X_train.values, y_train)
y_pred = logreg.predict(X_test)

ما قبلاً با مدل خود پیش بینی کرده ایم! بیایید به 3 ردیف اول نگاه کنیم X_train برای اینکه ببینیم از چه داده هایی استفاده کرده ایم:

X_train(:3)

کد بالا خروجی می دهد:

       Area          Perimeter     Major_Axis_Length    Minor_Axis_Length    Convex_Area   Equiv_Diameter       Eccentricity  Solidity      Extent        Roundness     Aspect_Ration        Compactness
0      -1.098308     -0.936518     -0.607941            -1.132551            -1.082768     -1.122359            0.458911      -1.078259     0.562847      -0.176041     0.236617             -0.360134
1      -0.501526     -0.468936     -0.387303            -0.376176            -0.507652     -0.475015            0.125764      0.258195      0.211703      0.094213      -0.122270            0.019480
2      0.012372      -0.209168     -0.354107            0.465095              0.003871      0.054384            -0.453911     0.432515      0.794735      0.647084      -0.617427            0.571137

و در 3 پیش بینی اول در y_pred برای دیدن نتایج:

y_pred(:3) 

این نتیجه در:

array((0, 0, 0))

برای آن سه ردیف، پیش‌بینی‌های ما این بود که آنها دانه‌های درجه یک هستند، Çerçevelik.

با رگرسیون لجستیک، به جای پیش بینی کلاس نهایی، مانند 0، همچنین می توانیم احتمال مربوط به ردیف را پیش بینی کنیم 0 کلاس این همان چیزی است که در واقع زمانی اتفاق می افتد که رگرسیون لجستیک داده ها را طبقه بندی می کند predict() متد سپس این پیش‌بینی را از یک آستانه عبور می‌کند تا یک کلاس “سخت” را برگرداند. برای پیش بینی احتمال مربوط به یک کلاس، predict_proba() استفاده می شود:

y_pred_proba = logreg.predict_proba(X_test)

بیایید به 3 مقدار اول پیش بینی احتمالات y نیز نگاهی بیندازیم:

y_pred_proba(:3) 

کدام خروجی ها:

        # class 0   class 1   
array(((0.54726628, 0.45273372),
       (0.56324527, 0.43675473),
       (0.86233349, 0.13766651)))

حالا به جای سه صفر برای هر کلاس یک ستون داریم. در ستون سمت چپ، با شروع 0.54726628، احتمال داده های مربوط به کلاس هستند 0; و در ستون سمت راست، با شروع 0.45273372، احتمال آن مربوط به کلاس است 1.

اطلاعات بیشتری وجود دارد روی چگونه خروجی پیش بینی شده ساخته شد در واقع اینطور نبود 0، اما احتمال کلاس 55٪ است 0و احتمال کلاس 45 درصد است 1. این سطوح سه مورد اول را نشان می دهد X_test نقاط داده مربوط به کلاس 0، فقط در مورد سومین نقطه داده با احتمال 86٪ کاملاً واضح هستند – و نه چندان برای دو نقطه داده اول.

هنگام برقراری ارتباط یافته ها با استفاده از روش های ML – معمولاً بهتر است یک کلاس نرم و احتمال مربوط به آن را به عنوان “اعتماد به نفس” از آن طبقه بندی

هنگامی که به مدل عمیق تر برویم، در مورد روش محاسبه آن بیشتر صحبت خواهیم کرد. در این زمان می توانیم به مرحله بعدی برویم.

ارزیابی مدل با گزارش های طبقه بندی

مرحله سوم این است که ببینید مدل چگونه عمل می کند روی داده های تست ما میتوانیم import Scikit-Learn classification_report() و از ما عبور کنید y_test و y_pred به عنوان استدلال پس از آن، ما می توانیم print پاسخ آن

گزارش طبقه بندی حاوی بیشترین استفاده از معیارهای طبقه بندی است، مانند دقت، درستی، به خاطر آوردن، امتیاز f1، و دقت.

1. دقت، درستی: برای درک اینکه چه مقادیر پیش‌بینی درستی توسط طبقه‌بندی‌کننده ما صحیح در نظر گرفته شده است. دقت آن مقادیر مثبت واقعی را بر هر چیزی که به عنوان مثبت پیش بینی شده بود تقسیم می کند:

$$
دقت = \frac{\text{مثبت واقعی}}{\text{مثبت واقعی} + \متن{مثبت نادرست}}
$$

2. به خاطر آوردن: برای درک اینکه چه تعداد از موارد مثبت واقعی توسط طبقه بندی کننده ما شناسایی شده است. فراخوان با تقسیم مثبت های واقعی بر هر چیزی که باید مثبت پیش بینی می شد محاسبه می شود:

$$
recall = \frac{\text{true positive}}{\text{true positive} + \text{غیر غلط}}
$$

3. امتیاز F1: متعادل است یا میانگین هارمونیک دقت و یادآوری کمترین مقدار 0 و بیشترین مقدار 1 است. When f1-score برابر با 1 است، به این معنی است که همه کلاس ها به درستی پیش بینی شده اند – این یک امتیاز بسیار سخت برای به دست آوردن با داده های واقعی است:

$$
\text{f1-score} = 2* \frac{\text{precision} * \text{recall}}{\text{precision} + \text{recal}}
$$

4. دقت: تشریح می کند که طبقه بندی کننده ما چند پیش بینی درست انجام داده است. کمترین مقدار دقت 0 و بیشترین مقدار 1 است. این مقدار معمولاً در 100 ضرب می شود تا یک درصد بدست آید:

$$
دقت = \frac{\text{تعداد پیش‌بینی‌های صحیح}}{\text{تعداد کل پیش‌بینی‌ها}}
$$

from sklearn.metrics import classification_report
cr = classification_report(y_test, y_pred)
print(cr)

سپس می توانیم به خروجی گزارش طبقه بندی نگاه کنیم:

                precision    recall  f1-score   support

           0       0.83      0.91      0.87       316
           1       0.90      0.81      0.85       309

    accuracy                           0.86       625
   macro avg       0.86      0.86      0.86       625
weighted avg       0.86      0.86      0.86       625

این نتیجه ماست. توجه کنید که precision، recall، f1-score، و accuracy معیارها همه بسیار بالا هستند، بالای 80٪ که ایده آل است – اما این نتایج احتمالاً تحت تأثیر همبستگی های بالا قرار گرفته اند و در دراز مدت پایدار نخواهند بود.

دقت مدل 86 درصد است، به این معنی که 14 درصد مواقع طبقه بندی را اشتباه می گیرد. ما این اطلاعات کلی را داریم، اما جالب است بدانید که آیا 14٪ اشتباهات در مورد طبقه بندی کلاس اتفاق می افتد یا خیر. 0 یا کلاس 1. برای تشخیص اینکه کدام کلاس ها به اشتباه شناسایی شده اند و در کدام فرکانس – می توانیم a را محاسبه و رسم کنیم ماتریس سردرگمی از پیش بینی های مدل ما

ارزیابی مدل با ماتریس سردرگمی

بیایید محاسبه کنیم و سپس ماتریس سردرگمی را رسم کنیم. پس از انجام این کار، می توانیم هر قسمت از آن را درک کنیم. برای ترسیم ماتریس سردرگمی، از Scikit-Learn استفاده می کنیم confusion_matrix()، که ما انجام خواهیم داد import از metrics مدول.

تجسم ماتریس سردرگمی با استفاده از Seaborn آسانتر است heatmap(). بنابراین، پس از تولید آن، ماتریس سردرگمی خود را به عنوان آرگومان برای نقشه حرارتی ارسال می کنیم:

from sklearn.metrics import confusion_matrix

cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d')

5. ماتریس سردرگمی: ماتریس نشان می دهد که چند نمونه مدل برای هر کلاس درست یا غلط است. مقادیری که درست و به درستی پیش بینی شده بودند نامیده می شوند نکات مثبت واقعیو آنهایی که مثبت پیش بینی شده بودند اما مثبت نبودند نامیده می شوند مثبت کاذب. همان نامگذاری از منفی های واقعی و منفی های کاذب برای مقادیر منفی استفاده می شود.

با نگاه کردن به نمودار ماتریس سردرگمی، می توانیم متوجه شویم که داریم 287 ارزش هایی که بودند 0 و به عنوان پیش بینی کرد 0 – یا نکات مثبت واقعی برای کلاس 0 (دانه های چرچولیک). ما همچنین داریم 250 نکات مثبت واقعی برای کلاس 1 (دانه های Ürgüp Sivrisi). مثبت های واقعی همیشه در مورب ماتریس قرار دارند که از سمت چپ بالا به سمت راست پایین می رود.

ما همچنین داریم 29 ارزش هایی که قرار بود باشند 0، اما پیش بینی شده است 1 (مثبت کاذب) و 59 ارزش هایی که بودند 1 و به عنوان پیش بینی کرد 0 (منفی های کاذب). با این اعداد، می توانیم بفهمیم که خطای مدل بیش از همه این است که منفی های کاذب را پیش بینی می کند. بنابراین، بیشتر می تواند دانه Ürgüp Sivrisi را به عنوان دانه Cerçevelik طبقه بندی کند.

این نوع خطا نیز با فراخوانی 81 درصدی کلاس توضیح داده می شود 1. توجه داشته باشید که معیارها به هم متصل هستند. و تفاوت در فراخوان به دلیل داشتن 100 نمونه کمتر از کلاس Ürgüp Sivrisi است. این یکی از پیامدهای داشتن چند نمونه کمتر از کلاس دیگر است. برای بهبود بیشتر یادآوری، می‌توانید با وزن‌های کلاس آزمایش کنید یا از نمونه‌های Ürgüp Sivrisi بیشتری استفاده کنید.

تاکنون اکثر مراحل سنتی علم داده را اجرا کرده ایم و از مدل رگرسیون لجستیک به عنوان جعبه سیاه استفاده کرده ایم.

اکنون زمان باز کردن جعبه سیاه و نگاه کردن به داخل آن فرا رسیده است تا به درک روش عملکرد رگرسیون لجستیک عمیق تر بپردازیم.

عمیق تر به چگونگی عملکرد رگرسیون لجستیک

را پسرفت کلمه تصادفی وجود ندارد، برای اینکه بفهمیم رگرسیون لجستیک چه می کند، می توانیم به یاد بیاوریم که رگرسیون خطی برادرش با داده ها چه می کند. فرمول رگرسیون خطی به صورت زیر بود:

$$
y = b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n
$$

که در آن ب₀ رهگیری رگرسیون بود، ب¹ ضریب و x¹ داده.

این معادله منجر به یک خط مستقیم شد که برای پیش‌بینی مقادیر جدید استفاده شد. با یادآوری مقدمه، تفاوت اکنون این است که ما مقادیر جدید را پیش‌بینی نمی‌کنیم، بلکه یک کلاس را پیش‌بینی می‌کنیم. بنابراین آن خط مستقیم باید تغییر کند. با رگرسیون لجستیک، یک غیر خطی را معرفی می کنیم و اکنون پیش بینی با استفاده از یک منحنی به جای یک خط انجام می شود:

توجه داشته باشید که در حالی که خط رگرسیون خطی به حرکت خود ادامه می دهد و از مقادیر بی نهایت پیوسته ساخته شده است، منحنی رگرسیون لجستیک را می توان در وسط تقسیم کرد و دارای افراط در مقادیر 0 و 1 است. این شکل “S” دلیلی است که داده ها را طبقه بندی می کند – نقاطی که نزدیکتر هستند یا سقوط می کنند روی بالاترین اندام متعلق به کلاس 1 است، در حالی که نقاطی که در ربع پایینی یا نزدیک به 0 قرار دارند، متعلق به کلاس 0 هستند. وسط “S” وسط بین 0 و 1 است، 0.5 – این آستانه برای نقاط رگرسیون لجستیک

ما قبلاً تفاوت بصری بین رگرسیون لجستیک و خطی را درک کرده ایم، اما در مورد فرمول چطور؟ فرمول رگرسیون لجستیک به شرح زیر است:

$$
y = b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n
$$

همچنین می توان آن را به صورت زیر نوشت:

$$
y_{prob} = \frac{1}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}}
$$

یا حتی به صورت زیر نوشته شود:

$$
y_{prob} = \frac{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}}
$$

در معادله بالا، به جای مقدار آن، احتمال ورودی را داریم. عدد 1 را به‌عنوان شماره‌کننده‌اش دارد، بنابراین می‌تواند مقداری بین 0 و 1، و 1 به اضافه یک مقدار در مخرج آن به‌دست آورد، به طوری که مقدار آن 1 و چیزی باشد – این بدان معناست که کل نتیجه کسر نمی‌تواند بزرگ‌تر از 1 باشد. .

و مقداری که در مخرج است چقدر است؟ این است ه، پایه لگاریتم طبیعی (تقریباً 2.718282)، به توان رگرسیون خطی افزایش یافته است:

$$
e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}
$$

روش دیگری برای نوشتن آن خواهد بود:

$$
ln \left( \frac{p}{1-p} \right) = {(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}
$$

در آخرین معادله، لوگاریتم لگاریتم طبیعی (پایه e) است و پ احتمال است، بنابراین لگاریتم احتمال نتیجه همان نتیجه رگرسیون خطی است.

به عبارت دیگر، با نتیجه رگرسیون خطی و لگاریتم طبیعی، می‌توانیم به احتمال یک ورودی مربوط به کلاس طراحی شده برسیم.

کل مشتق رگرسیون لجستیک process زیر است:

$$
p{X} = \frac{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}}
$$

$$
p(1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}) = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + \ldots + b_n * x_n)}
$$

$$
p + p*e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)} = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + \ ldots + b_n * x_n)}
$$

$$پ={ه}^{({ب}_0+{ب}_1\ast {\mathrm{ایکس}}_1+{ب}_2\ast {\mathrm{ایکس}}_2+{ب}_3\ast {\mathrm{ایکس}}_3+\dots +{ب}_n\ast {\mathrm{ایکس}}_n)}–پ\ast {ه}^{({ب}_0+{ب}_1\ast {\mathrm{ایکس}}_1+{ب}_2\ast {\mathrm{ایکس}}_2+{ب}_3\ast {\mathrm{ایکس}}_3+\dots +{ب}_n\ast {\mathrm{ایکس}}_n)}$$

$$
\frac{p}{1-p} = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + \ldots + b_n * x_n)}
$$

$$
ln \left( \frac{p}{1-p} \راست) = (b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + \ldots + b_n * x_n)
$$

این بدان معناست که مدل رگرسیون لجستیک دارای ضرایب و مقدار رهگیری نیز می باشد. زیرا از رگرسیون خطی استفاده می کند و با لگاریتم طبیعی یک جزء غیر خطی به آن اضافه می کند (e).

ما می‌توانیم مقادیر ضرایب و فاصله مدل خود را ببینیم، همانطور که برای رگرسیون خطی انجام دادیم، با استفاده از coef_ و intercept_ خواص:

logreg.coef_

که ضرایب هر یک از 12 ویژگی را نشان می دهد:

array((( 1.43726172, -1.03136968,  0.24099522, -0.61180768,  1.36538261,
        -1.45321951, -1.22826034,  0.98766966,  0.0438686 , -0.78687889,
         1.9601197 , -1.77226097)))

logreg.intercept_

که منجر به:

array((0.08735782))

با ضرایب و مقادیر رهگیری، می توانیم احتمالات پیش بینی شده داده های خود را محاسبه کنیم. بیایید اولی را بگیریم X_test دوباره مقادیر، به عنوان مثال:

X_test(:1)

این اولین ردیف را برمی گرداند X_test به عنوان یک آرایه NumPy:

array(((-1.09830823, -0.93651823, -0.60794138, -1.13255059, -1.0827684 ,
        -1.12235877,  0.45891056, -1.07825898,  0.56284738, -0.17604099,
         0.23661678, -0.36013424)))

مطابق معادله اولیه:

$$
p{X} = \frac{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n)}}
$$

که در python، ما داریم:

import math

lin_reg = logreg.intercept_(0) + \
((logreg.coef_(0)(0)* X_test(:1)(0)(0))+ \
(logreg.coef_(0)(1)* X_test(:1)(0)(1))+ \
(logreg.coef_(0)(2)* X_test(:1)(0)(2))+ \
(logreg.coef_(0)(3)* X_test(:1)(0)(3))+ \
(logreg.coef_(0)(4)* X_test(:1)(0)(4))+ \
(logreg.coef_(0)(5)* X_test(:1)(0)(5))+ \
(logreg.coef_(0)(6)* X_test(:1)(0)(6))+ \
(logreg.coef_(0)(7)* X_test(:1)(0)(7))+ \
(logreg.coef_(0)(8)* X_test(:1)(0)(8))+ \
(logreg.coef_(0)(9)* X_test(:1)(0)(9))+ \
(logreg.coef_(0)(10)* X_test(:1)(0)(10))+ \
(logreg.coef_(0)(11)* X_test(:1)(0)(11)))

px = math.exp(lin_reg)/(1 +(math.exp(lin_reg)))
px

این نتیجه در:

0.45273372469369133

اگر دوباره به آن نگاه کنیم predict_proba نتیجه اولی X_test خط، ما داریم:

logreg.predict_proba(X_test(:1))

این بدان معنی است که معادله اصلی رگرسیون لجستیک احتمال ورودی مربوط به کلاس را به ما می دهد. 1، برای اینکه بفهمیم کدام احتمال برای کلاس است 0، به سادگی می توانیم:

1 - px

توجه کنید که هر دو px و 1-px یکسان هستند predict_proba نتایج. رگرسیون لجستیک به این صورت محاسبه می شود و چرا پسرفت بخشی از نام آن است. اما در مورد اصطلاح چطور لجستیکی?

عبارت لجستیکی می آید از لوجیت، که تابعی است که قبلاً دیده ایم:

$$
ln \left( \frac{p}{1-p} \right)
$$

ما به تازگی آن را محاسبه کرده ایم px و 1-px. این logit است که به آن نیز گفته می شود شانس ورود از آنجایی که برابر است با لگاریتم شانس که در آن p یک احتمال است

نتیجه

در این راهنما، یکی از اساسی‌ترین الگوریتم‌های طبقه‌بندی یادگیری ماشین، یعنی رگرسیون لجستیک.

در ابتدا، ما رگرسیون لجستیک را به‌عنوان یک جعبه سیاه با کتابخانه یادگیری ماشینی Scikit-Learn پیاده‌سازی کردیم، و بعداً آن را گام به گام درک کردیم تا دلیل و مکان واژه‌های رگرسیون و لجستیک را روشن کنیم.

ما همچنین داده‌ها را کاوش و مطالعه کرده‌ایم و درک می‌کنیم که یکی از مهم‌ترین بخش‌های تحلیل علم داده است.

از اینجا، من به شما توصیه می کنم که با آن بازی کنید رگرسیون لجستیک چند طبقهرگرسیون لجستیک برای بیش از دو کلاس – می توانید همان الگوریتم رگرسیون لجستیک را برای مجموعه داده های دیگر که چندین کلاس دارند اعمال کنید و نتایج را تفسیر کنید.

همچنین به شما توصیه می کنم L1 و L2 را مطالعه کنید منظم سازی ها. آنها راهی برای “جریم کردن” داده های بالاتر به منظور نزدیک تر شدن به حالت عادی هستند و پیچیدگی مدل را حفظ می کنند، بنابراین الگوریتم می تواند به نتیجه بهتری برسد. پیاده سازی Scikit-Learn که ما استفاده کردیم قبلاً به طور پیش فرض دارای تنظیم L2 است. نکته دیگری که باید به آن نگاه کرد، متفاوت بودن آن است حل کننده ها، مانند lbgsکه عملکرد الگوریتم رگرسیون لجستیک را بهینه می کند.

همچنین مهم است که نگاهی به آماری رویکرد به رگرسیون لجستیک این دارد مفروضات در مورد رفتار داده ها و سایر آمارهایی که باید برای تضمین نتایج رضایت بخش وجود داشته باشد، مانند:

• مشاهدات مستقل هستند.
• بین متغیرهای توضیحی چند خطی وجود ندارد.
• هیچ نقطه پرت شدیدی وجود ندارد.
• یک رابطه خطی بین متغیرهای توضیحی و logit متغیر پاسخ وجود دارد.
• حجم نمونه به اندازه کافی بزرگ است.

توجه داشته باشید که چه تعداد از این مفروضات قبلاً در تجزیه و تحلیل و درمان داده ها پوشش داده شده است.

امیدوارم به بررسی آنچه که رگرسیون لجستیک در تمام رویکردهای مختلف خود ارائه می دهد ادامه دهید!