از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
راهنمای Heaps در پایتون
سرفصلهای مطلب
معرفی
فرودگاهی شلوغ را تصور کنید که هر دقیقه پروازهایی از آن بلند و فرود میآیند. همانطور که کنترلکنندههای ترافیک هوایی پروازها را بر اساس فوریت اولویتبندی میکنند، heaps به ما کمک میکند تا دادهها را بر اساس معیارهای خاص مدیریت و پردازش کنیم و اطمینان حاصل کنیم که «فوریترین» یا «مهمترین» دادهها همیشه در بالای صفحه قابل دسترسی هستند.
در این راهنما، ما سفری را برای درک انبوهی از زمین آغاز خواهیم کرد. ما با ابهام زدایی از چیستی پشته ها و ویژگی های ذاتی آنها شروع می کنیم. از آنجا، ما به پیادهسازی پشتهها توسط پایتون میپردازیم
heapqماژول، و مجموعه غنی از قابلیت های آن را کشف کنید. بنابراین، اگر تا به حال به این فکر کردهاید که چگونه میتوانید مجموعهای از دادههای پویا را که اغلب به بالاترین (یا پایینترین) اولویت نیاز است، بهطور کارآمد مدیریت کنید، در انتظار شما هستید.
هیپ چیست؟
اولین چیزی که می خواهید قبل از فرو رفتن در استفاده از پشته ها بدانید این است پشته چیست. یک پشته در دنیای ساختارهای داده به عنوان یک نیروگاه مبتنی بر درخت برجسته است، به ویژه در حفظ نظم و سلسله مراتب. در حالی که ممکن است برای چشمان آموزش ندیده شبیه یک درخت دوتایی باشد، تفاوت های ظریف در ساختار و قوانین حاکم بر آن به طور مشخص آن را متمایز می کند.
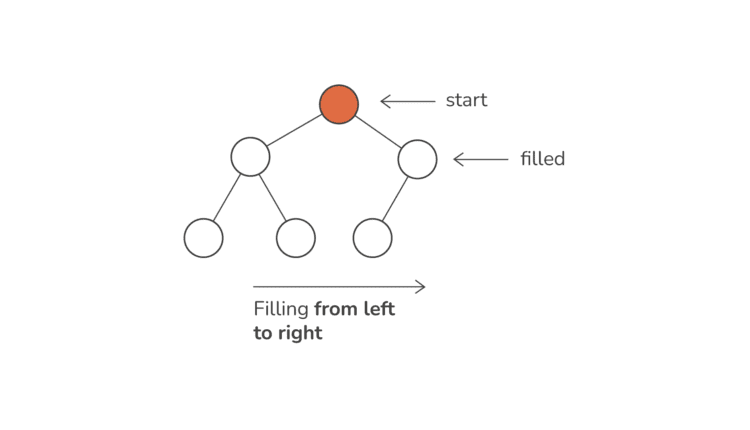
یکی از ویژگی های تعیین کننده یک پشته ماهیت آن به عنوان یک است درخت دودویی کامل. این بدان معنی است که هر سطح درخت، به جز آخرین سطح، به طور کامل پر شده است. در این آخرین سطح، گره ها از چپ به راست پر می شوند. چنین ساختاری تضمین میکند که پشتهها را میتوان بهطور کارآمد با استفاده از آرایهها یا فهرستها نشان داد و دستکاری کرد، با موقعیت هر عنصر در آرایه منعکس کننده محل قرارگیری آن در درخت.

با این حال، جوهر واقعی یک توده در آن نهفته است مرتب سازی. در یک حداکثر پشته، مقدار هر گره داده شده از مقادیر فرزندان خود فراتر می رود یا برابر است و بزرگترین عنصر را درست در ریشه قرار می دهد. از سوی دیگر، الف پشته دقیقه بر اساس اصل مخالف عمل می کند: مقدار هر گره یا کمتر یا برابر با مقادیر فرزندان آن است، و اطمینان می دهد که کوچکترین عنصر در ریشه قرار می گیرد.

توصیه: شما می توانید یک پشته را به عنوان یک تجسم کنید هرم اعداد. برای یک پشته حداکثر، همانطور که از پایه به قله صعود می کنید، اعداد افزایش می یابد و به حداکثر مقدار در اوج می رسد. در مقابل، یک پشته کوچک با حداقل مقدار در اوج خود شروع می شود، با اعداد که با حرکت به سمت پایین افزایش می یابند.
همانطور که پیشرفت می کنیم، عمیق تر به این می پردازیم که چگونه این ویژگی های ذاتی heap ها عملیات کارآمد را ممکن می کند و چگونه پایتون heapq ماژول به طور یکپارچه انبوهی را در تلاش های کدنویسی ما ادغام می کند.
ویژگی ها و خواص هیپ ها
Heap ها با ساختار منحصر به فرد و اصول نظم دهی خود، مجموعه ای از ویژگی ها و ویژگی های متمایز را ارائه می دهند که آنها را در سناریوهای محاسباتی مختلف ارزشمند می کند.
اول و مهمتر از همه، پشته ها هستند ذاتا کارآمد. ساختار درختی آنها، به ویژه فرمت درخت دودویی کامل، تضمین می کند که عملیاتی مانند درج و استخراج عناصر اولویت (حداکثر یا حداقل) را می توان در زمان لگاریتمی انجام داد. O (log n). این کارایی برای الگوریتمها و برنامههایی که نیاز به دسترسی مکرر به عناصر اولویت دارند، امتیازی است.
یکی دیگر از ویژگی های قابل توجه کپه ها آنها است کارایی حافظه. از آنجایی که هپها را میتوان با استفاده از آرایهها یا لیستها بدون نیاز به اشارهگرهای صریح به گرههای فرزند یا والد نمایش داد، در فضا صرفهجویی میکنند. موقعیت هر عنصر در آرایه مطابق با قرارگیری آن در درخت است که امکان پیمایش و دستکاری قابل پیش بینی و مستقیم را فراهم می کند.
خاصیت سفارش دهی هپ ها، چه به صورت max heap یا min heap، این امر را تضمین می کند ریشه همیشه عنصر بالاترین اولویت را دارد. این ترتیب ثابت چیزی است که امکان دسترسی سریع به عنصر با اولویت را بدون نیاز به جستجو در کل ساختار فراهم می کند.
علاوه بر این، پشته ها هستند همه کاره. در حالی که هپ های باینری (که در آن هر والدین حداکثر دو فرزند دارند) رایج ترین هستند، هپ ها را می توان به بیش از دو فرزند تعمیم داد، که به عنوان شناخته شده است. پشته های d-ary. این انعطاف پذیری امکان تنظیم دقیق بر اساس موارد استفاده خاص و الزامات عملکرد را فراهم می کند.
در نهایت، پشته ها هستند خود تنظیم. هر زمان که عناصر اضافه یا حذف شوند، ساختار خود را مجدداً تنظیم می کند تا خواص خود را حفظ کند. این تعادل پویا تضمین می کند که هیپ همیشه برای عملیات اصلی خود بهینه می ماند.
با کاوش عمیقتر در پیادهسازی و کاربردهای عملی پایتون، پتانسیل واقعی heaps در برابر ما آشکار میشود.
انواع هیپ ها
همه توده ها یکسان ایجاد نمی شوند. بسته به ترتیب و ویژگی های ساختاری، هپ ها را می توان به انواع مختلفی دسته بندی کرد که هر کدام مجموعه ای از کاربردها و مزایای خاص خود را دارند. دو دسته اصلی هستند حداکثر پشته و پشته دقیقه.
متمایزترین ویژگی الف حداکثر پشته این است که مقدار هر گره داده شده بزرگتر یا برابر با مقادیر فرزندان آن است. این تضمین می کند که بزرگترین عنصر در پشته همیشه در ریشه قرار دارد. چنین ساختاری به ویژه زمانی مفید است که نیاز به دسترسی مکرر به عنصر حداکثر وجود داشته باشد، مانند اجرای صف های اولویت دار خاص.
همتای حداکثر هیپ، a پشته دقیقه تضمین می کند که مقدار هر گره داده شده کمتر یا برابر با مقادیر فرزندان آن باشد. این کوچکترین عنصر پشته را در ریشه قرار می دهد. تودههای حداقل در سناریوهایی که کمترین عنصر از اهمیت بالایی برخوردار است، مانند الگوریتمهایی که با پردازش بلادرنگ داده سروکار دارند، بسیار ارزشمند هستند.
فراتر از این دسته بندی های اولیه، هپ ها را می توان بر اساس فاکتور انشعاب آنها نیز متمایز کرد:
در حالی که پشته های باینری رایج ترین هستند، با هر یک از والدین حداکثر دو فرزند، مفهوم هپ ها را می توان به گره هایی که بیش از دو فرزند دارند تعمیم داد. در یک پشته d-ary، هر گره حداکثر دارد d فرزندان. این تنوع را می توان برای سناریوهای خاص، مانند کاهش ارتفاع درخت برای سرعت بخشیدن به عملیات خاص، بهینه کرد.
دوجمله ای هیپ مجموعه ای از درختان دو جمله ای است که به صورت بازگشتی تعریف می شوند. پشته های دوجمله ای در اجرای صف های اولویت دار استفاده می شوند و عملیات ادغام کارآمد را ارائه می دهند.
نام آن از دنباله معروف فیبوناچی، the پشته فیبوناچی زمان اجرای استهلاک بهتری را برای بسیاری از عملیات در مقایسه با پشته های باینری یا دو جمله ای ارائه می دهد. آنها به ویژه در الگوریتم های بهینه سازی شبکه مفید هستند.
پیاده سازی هیپ پایتون – The heapq مدول
پایتون یک ماژول داخلی برای عملیات پشته ارائه می دهد – the heapq مدول. این ماژول مجموعه ای از توابع مرتبط با heap را ارائه می دهد که به توسعه دهندگان اجازه می دهد تا لیست ها را به heap تبدیل کرده و بدون نیاز به پیاده سازی سفارشی، عملیات های مختلف heap را انجام دهند. بیایید به تفاوتهای ظریف این ماژول و اینکه چگونه قدرت پشتهها را برای شما به ارمغان میآورد، بپردازیم.
را heapq ماژول یک نوع داده پشته متمایز ارائه نمی دهد. در عوض، توابعی را ارائه میدهد که روی لیستهای پایتون معمولی کار میکنند، آنها را تبدیل میکند و بهعنوان آنها رفتار میکند پشته های دوتایی.
این رویکرد هم از نظر حافظه کارآمد است و هم به طور یکپارچه با ساختارهای داده موجود پایتون ادغام می شود.
یعنی همین پشته ها به صورت لیست نشان داده می شوند که در heapq. زیبایی این نمایش در سادگی آن است – سیستم فهرست فهرست مبتنی بر صفر به عنوان یک درخت باینری ضمنی عمل می کند. برای هر عنصر معین در موقعیت i، آن:
- کودک چپ در موقعیت است
2*i + 1 - کودک راست در موقعیت است
2*i + 2 - گره والد در موقعیت است
(i-1)//2

این ساختار ضمنی تضمین می کند که نیازی به نمایش درخت باینری مبتنی بر گره جداگانه نیست، عملیات را ساده می کند و استفاده از حافظه را به حداقل می رساند.
پیچیدگی فضا: Heap ها معمولاً به صورت درخت های باینری پیاده سازی می شوند، اما نیازی به ذخیره اشاره گرهای صریح برای گره های فرزند ندارند. این باعث می شود آنها در فضای کارآمد با پیچیدگی فضایی بر) برای ذخیره سازی n عنصر
ذکر این نکته ضروری است که heapq مدول به صورت پیشفرض تعداد min heap ایجاد میکند. این بدان معنی است که کوچکترین عنصر همیشه در ریشه (یا اولین موقعیت در لیست) است. اگر به یک پشته حداکثر نیاز دارید، باید ترتیب را با ضرب عناصر در برعکس کنید -1 یا از یک تابع مقایسه سفارشی استفاده کنید.
پایتون heapq ماژول مجموعه ای از توابع را ارائه می دهد که به توسعه دهندگان اجازه می دهد تا عملیات پشته های مختلف را در لیست ها انجام دهند.
توجه داشته باشید: برای استفاده از heapq ماژول در برنامه خود، باید آن را با استفاده از ساده وارد کنید import heapq.
در بخشهای بعدی، به عمق هر یک از این عملیاتهای اساسی میپردازیم، مکانیک و موارد استفاده آنها را بررسی میکنیم.
چگونه یک لیست را به یک پشته تبدیل کنیم
را heapify() تابع نقطه شروع بسیاری از کارهای مرتبط با پشته است. یک تکرار (معمولاً یک لیست) می گیرد و عناصر آن را در جای خود مجدداً مرتب می کند تا ویژگی های یک پشته کوچک را برآورده کند:
import heapq
data = (3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5)
heapq.heapify(data)
print(data)
با این کار یک لیست دوباره ترتیب داده شده است که نشان دهنده یک پشته حداقل معتبر است:
(1, 1, 2, 3, 3, 9, 4, 6, 5, 5, 5)
پیچیدگی زمانی: تبدیل یک لیست نامرتب به پشته با استفاده از heapify تابع یک است بر) عمل. این ممکن است خلاف واقع به نظر برسد، همانطور که ممکن است انتظار داشته باشید O(nlogn)، اما با توجه به ویژگی های ساختار درختی، می توان آن را در زمان خطی به دست آورد.
چگونه یک عنصر را به Heap اضافه کنیم
را heappush() تابع به شما این امکان را می دهد که یک عنصر جدید را در پشته وارد کنید و در عین حال ویژگی های پشته را حفظ کنید:
import heapq
heap = ()
heapq.heappush(heap, 5)
heapq.heappush(heap, 3)
heapq.heappush(heap, 7)
print(heap)
با اجرای کد، لیستی از عناصری که ویژگی min heap را حفظ می کنند به شما ارائه می دهد:
(3, 5, 7)
پیچیدگی زمانی: عملیات درج در یک پشته، که شامل قرار دادن یک عنصر جدید در پشته با حفظ ویژگی heap است، دارای پیچیدگی زمانی است. O(logn). این به این دلیل است که در بدترین حالت، این عنصر ممکن است از برگ به ریشه سفر کند.
نحوه حذف و برگرداندن کوچکترین عنصر از هیپ
را heappop() تابع کوچکترین عنصر را از پشته (ریشه در یک پشته کوچک) استخراج و برمی گرداند. پس از حذف، تضمین میکند که لیست یک پشته معتبر باقی میماند:
import heapq
heap = (1, 3, 5, 7, 9)
print(heapq.heappop(heap))
print(heap)
توجه داشته باشید: را heappop() در الگوریتمهایی که به پردازش عناصر به ترتیب صعودی نیاز دارند، مانند الگوریتم مرتبسازی هیپ، یا هنگام اجرای صفهای اولویتی که وظایف بر اساس فوریت آنها اجرا میشوند، بسیار ارزشمند است.
با این کار کوچکترین عنصر و لیست باقی مانده خروجی می شود:
1
(3, 7, 5, 9)
اینجا، 1 کوچکترین عنصر از heap، و لیست باقیمانده ویژگی heap را حتی پس از حذف ما حفظ کرده است 1.
پیچیدگی زمانی: حذف عنصر ریشه (که کوچکترین در یک پشته کوچک یا بزرگترین در یک پشته حداکثر است) و سازماندهی مجدد پشته نیز نیاز دارد. O(logn) زمان.
چگونه یک مورد جدید را فشار دهید و کوچکترین مورد را پاپ کنید
را heappushpop() تابع یک عملیات ترکیبی است که یک آیتم جدید را روی پشته هل می دهد و سپس ظاهر می شود و کوچکترین آیتم را از پشته برمی گرداند:
import heapq
heap = (3, 5, 7, 9)
print(heapq.heappushpop(heap, 4))
print(heap)
این خروجی خواهد شد 3، کوچکترین عنصر، و چاپ جدید heap لیستی که اکنون شامل می شود 4 در حین حفظ خاصیت heap:
3
(4, 5, 7, 9)
توجه داشته باشید: با استفاده از heappushpop() عملکرد کارآمدتر از انجام عملیات هل دادن یک عنصر جدید و بیرون زدن کوچکترین عنصر به طور جداگانه است.
چگونه کوچکترین مورد را جایگزین کنیم و یک مورد جدید را فشار دهیم
را heapreplace() تابع کوچکترین عنصر را باز می کند و یک عنصر جدید را روی پشته هل می دهد، همه در یک عملیات کارآمد:
import heapq
heap = (1, 5, 7, 9)
print(heapq.heapreplace(heap, 4))
print(heap)
این چاپ می کند 1، کوچکترین عنصر، و لیست اکنون شامل 4 است و ویژگی heap را حفظ می کند:
1
(4, 5, 7, 9)
توجه داشته باشید: heapreplace() در سناریوهای پخش جریانی که میخواهید کوچکترین عنصر فعلی را با یک مقدار جدید جایگزین کنید مفید است، مانند عملیات پنجره چرخشی یا وظایف پردازش داده در زمان واقعی.
یافتن اکستریم های متعدد در هیپ پایتون
nlargest(n, iterable(, key)) و nsmallest(n, iterable(, key)) توابع برای بازیابی چندین عنصر بزرگ یا کوچک از یک تکرار شونده طراحی شده اند. آنها می توانند کارآمدتر از مرتب کردن کل تکرار شونده در زمانی که شما فقط به چند مقدار شدید نیاز دارید. به عنوان مثال، فرض کنید لیست زیر را دارید و می خواهید سه مقدار کوچک و سه مقدار بزرگ را در لیست پیدا کنید:
data = (3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5)
اینجا، nlargest() و nsmallest() توابع می توانند مفید باشند:
import heapq
data = (3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5)
print(heapq.nlargest(3, data)) # Outputs (9, 6, 5)
print(heapq.nsmallest(3, data)) # Outputs (1, 1, 2)
این به شما دو لیست می دهد – یکی شامل سه مقدار بزرگ و دیگری شامل سه کوچکترین مقدار از data لیست:
(9, 6, 5)
(1, 1, 2)
چگونه هپ سفارشی خود را بسازید
در حالی که پایتون heapq ماژول مجموعه ای قوی از ابزارها را برای کار با heap ها فراهم می کند، سناریوهایی وجود دارد که رفتار پیش فرض min heap ممکن است کافی نباشد. چه به دنبال پیادهسازی حداکثر هیپ باشید یا به هیپ نیاز داشته باشید که بر اساس توابع مقایسه سفارشی عمل کند، ساخت یک پشته سفارشی میتواند پاسخگو باشد. بیایید بررسی کنیم که چگونه انبوهی را برای نیازهای خاص تنظیم کنیم.
پیاده سازی Max Heap با استفاده از heapq
به صورت پیش فرض، heapq ایجاد می کند کپه های دقیقه. با این حال، با یک ترفند ساده، می توانید از آن برای پیاده سازی یک max heap استفاده کنید. ایده این است که ترتیب عناصر را با ضرب آنها در معکوس کنیم -1 قبل از اضافه کردن آنها به پشته:
import heapq
class MaxHeap:
def __init__(self):
self.heap = ()
def push(self, val):
heapq.heappush(self.heap, -val)
def pop(self):
return -heapq.heappop(self.heap)
def peek(self):
return -self.heap(0)
با این رویکرد، بزرگترین عدد (از نظر قدر مطلق) به کوچکترین تبدیل می شود، که اجازه می دهد heapq عملکردی برای حفظ ساختار پشته حداکثر.
Heaps با توابع مقایسه سفارشی
گاهی اوقات، ممکن است به یک پشته نیاز داشته باشید که فقط بر اساس ترتیب طبیعی عناصر مقایسه نشود. به عنوان مثال، اگر با اشیاء پیچیده کار می کنید یا معیارهای مرتب سازی خاصی دارید، یک تابع مقایسه سفارشی ضروری می شود.
برای رسیدن به این هدف، می توانید عناصر را در یک کلاس کمکی قرار دهید که عملگرهای مقایسه را لغو می کند:
import heapq
class CustomElement:
def __init__(self, obj, comparator):
self.obj = obj
self.comparator = comparator
def __lt__(self, other):
return self.comparator(self.obj, other.obj)
def custom_heappush(heap, obj, comparator=lambda x, y: x < y):
heapq.heappush(heap, CustomElement(obj, comparator))
def custom_heappop(heap):
return heapq.heappop(heap).obj
با این تنظیمات، می توانید هر تابع مقایسه کننده سفارشی را تعریف کنید و از آن با heap استفاده کنید.
نتیجه
Heaps عملکرد قابل پیش بینی را برای بسیاری از عملیات ارائه می دهد و آنها را به انتخابی مطمئن برای وظایف مبتنی بر اولویت تبدیل می کند. با این حال، در نظر گرفتن الزامات و ویژگی های خاص برنامه در دست ضروری است. در برخی موارد، بهینه سازی اجرای heap یا حتی انتخاب ساختارهای داده جایگزین ممکن است عملکرد بهتری در دنیای واقعی داشته باشد.
Heaps، همانطور که ما از پستی و بلندی آن سفر کردیم، بیش از یک ساختار داده دیگر هستند. آنها ترکیبی از کارایی، ساختار و سازگاری را نشان می دهند. از ویژگی های اساسی آنها تا پیاده سازی آنها در پایتون heapq ماژول، heaps یک راه حل قوی برای تعداد بی شماری از چالش های محاسباتی، به ویژه آنهایی که حول محور اولویت هستند، ارائه می دهد.
منتشر شده در 1402-12-26 02:39:58



