رمزگذارهای خودکار برای بازسازی تصویر در پایتون و کراس

معرفی

امروزه تقریباً در هر برنامه ای که استفاده می کنیم – گوش دادن به موسیقی – حجم عظیمی از داده داریم روی Spotify، در حال مرور تصاویر دوستان روی اینستاگرام، یا شاید در حال تماشای یک تریلر جدید روی یوتیوب. همیشه داده هایی از سرورها به شما منتقل می شود.

این برای یک کاربر مشکلی ایجاد نمی کند. اما تصور کنید که هزاران، اگر نگوییم میلیون ها، درخواست با داده های بزرگ را به طور همزمان مدیریت کنید. این جریان داده ها باید به نحوی کاهش یابد تا بتوانیم از نظر فیزیکی آنها را در اختیار کاربران قرار دهیم – اینجاست که متراکم سازی داده ها لگد وارد می کند.

تکنیک های فشرده سازی زیادی وجود دارد و از نظر کاربرد و سازگاری متفاوت است. به عنوان مثال برخی از تکنیک های فشرده سازی فقط کار می کنند روی فایل های صوتی مانند معروف MPEG-2 Audio Layer III کدک (MP3).

دو نوع اصلی فشرده سازی وجود دارد:

• بدون ضرر: یکپارچگی و دقت داده‌ها ترجیح داده می‌شود، حتی اگر زیاد «ریش نکنیم».
• باخت: یکپارچگی و دقت داده‌ها به اندازه سرعتی که می‌توانیم آن‌ها را ارائه کنیم مهم نیست – یک انتقال ویدیوی بی‌درنگ را تصور کنید، جایی که «زنده» بودن مهم‌تر از داشتن ویدیوی با کیفیت بالا است.

به عنوان مثال، با استفاده از رمزگذارهای خودکار، می توانیم این تصویر را تجزیه کرده و آن را به صورت کد 32 برداری زیر نمایش دهیم. با استفاده از آن می توانیم تصویر را بازسازی کنیم. البته این یک نمونه است زیان ده فشرده سازی، زیرا ما مقدار زیادی از اطلاعات را از دست داده ایم.

اگرچه، می‌توانیم دقیقاً از همان تکنیک برای انجام دقیق‌تر این کار، با اختصاص فضای بیشتر برای نمایش استفاده کنیم:

Autoencoder چیست؟

رمزگذار خودکار، طبق تعریف، تکنیکی برای رمزگذاری خودکار چیزی است. با استفاده از یک شبکه عصبی، رمزگذار خودکار می‌تواند یاد بگیرد که چگونه داده‌ها (در مورد ما، تصاویر) را به بیت‌های نسبتاً کوچکی از داده‌ها تجزیه کند و سپس با استفاده از آن نمایش، داده‌های اصلی را تا جایی که می‌تواند نزدیک به اصلی بازسازی کند.

دو جزء کلیدی در این کار وجود دارد:

• رمزگذار: یاد می گیرد که چگونه ورودی اصلی را در یک رمزگذاری کوچک فشرده کند
• رمزگشا: یاد می گیرد که چگونه داده های اصلی را از کدگذاری ایجاد شده توسط رمزگذار

این دو با هم در همزیستی آموزش داده می شوند تا کارآمدترین نمایش داده را به دست آورند که بتوانیم داده های اصلی را بدون از دست دادن مقدار زیادی از آن بازسازی کنیم.

اعتبار: دروازه تحقیق

رمزگذار

را رمزگذار وظیفه یافتن کوچکترین نمایش ممکن از داده هایی است که می تواند ذخیره کند – استخراج برجسته ترین ویژگی های داده های اصلی و نمایش آن به گونه ای که رمزگشا بتواند آن را درک کند.

به این فکر کنید که انگار می‌خواهید چیزی را به خاطر بسپارید، مثلاً یک عدد بزرگ را به خاطر بسپارید – سعی می‌کنید الگویی را در آن بیابید که بتوانید آن الگو را به خاطر بسپارید و کل دنباله را از آن الگو بازیابی کنید، زیرا به خاطر سپردن یک عدد کوتاه‌تر آسان خواهد بود. الگوی نسبت به عدد کامل

رمزگذارها در ساده ترین شکل خود ساده هستند شبکه های عصبی مصنوعی (ANN). اگرچه، رمزگذارهای خاصی وجود دارند که از آن استفاده می کنند شبکه های عصبی کانولوشنال (CNNs)، که یک نوع بسیار خاص از ANN است.

رمزگذار داده های ورودی را می گیرد و یک نسخه کدگذاری شده از آن – داده های فشرده شده – تولید می کند. سپس می‌توانیم از آن داده‌های فشرده برای ارسال آن به کاربر استفاده کنیم، جایی که رمزگشایی و بازسازی می‌شود. بیایید نگاهی به رمزگذاری برای a بیاندازیم LFW نمونه مجموعه داده:

رمزگذاری در اینجا برای ما چندان منطقی نیست، اما برای رمزگشا کافی است. حال، طرح این سؤال صحیح است:

اما رمزگذار چگونه بود فرا گرفتن برای فشرده سازی تصاویر به این صورت؟

اینجاست که همزیستی در حین تمرین مطرح می شود.

رمزگشا

را رمزگشا به روشی مشابه رمزگذار کار می کند، اما برعکس. یاد می گیرد به جای تولید، این نمایش های کد فشرده را بخواند و تصاویر را بر اساس تولید کند روی آن اطلاعات بدیهی است که هدف آن به حداقل رساندن ضرر در حین بازسازی است.

خروجی با مقایسه تصویر بازسازی شده با تصویر اصلی، با استفاده از خطای میانگین مربع (MSE) ارزیابی می شود – هر چه بیشتر شبیه به تصویر اصلی باشد، خطا کوچکتر است.

در این مرحله، ما به عقب انتشار می دهیم و تمام پارامترها را از رمزگشا به رمزگذار به روز می کنیم. بنابراین، بر اساس روی تفاوت بین تصاویر ورودی و خروجی، رمزگشا و رمزگذار هر دو در کار خود ارزیابی می شوند و پارامترهای خود را برای بهتر شدن به روز می کنند.

ساخت رمزگذار خودکار

کراس یک چارچوب پایتون است که ساخت شبکه های عصبی را ساده تر می کند. این به ما اجازه می دهد تا لایه هایی از انواع مختلف را برای ایجاد یک شبکه عصبی عمیق روی هم قرار دهیم – که ما برای ساخت یک رمزگذار خودکار انجام خواهیم داد.

ابتدا اجازه دهید Keras را با استفاده از آن نصب کنیم pip:

$ pip install keras

پیش پردازش داده ها

دوباره، ما از آن استفاده خواهیم کرد مجموعه داده LFW. طبق معمول، با پروژه‌هایی مانند این، داده‌ها را از قبل پردازش می‌کنیم تا رمزگذار خودکارمان بتواند کار خود را آسان‌تر کند.

برای این، ابتدا چند مسیر را تعریف می کنیم که به مجموعه داده مورد استفاده ما منتهی می شود:

ATTRS_NAME = "lfw_attributes.txt"


IMAGES_NAME = "lfw-deepfunneled.tgz"


RAW_IMAGES_NAME = "lfw.tgz"

سپس، ما از دو تابع استفاده می کنیم – یکی برای تبدیل ماتریس خام به یک تصویر و تغییر سیستم رنگ به RGB:

def decode_image_from_raw_bytes(raw_bytes):
    img = cv2.imdecode(np.asarray(bytearray(raw_bytes), dtype=np.uint8), 1)
    img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    return img

و دیگری برای بارگیری مجموعه داده و تطبیق آن با نیازهای ما:

def load_lfw_dataset(
        use_raw=False,
        dx=80, dy=80,
        dimx=45, dimy=45):

    
    df_attrs = pd.read_csv(ATTRS_NAME, sep='\t', skiprows=1)
    df_attrs = pd.DataFrame(df_attrs.iloc(:, :-1).values, columns=df_attrs.columns(1:))
    imgs_with_attrs = set(map(tuple, df_attrs(("person", "imagenum")).values))

    
    all_photos = ()
    photo_ids = ()

    
    
    with tarfile.open(RAW_IMAGES_NAME if use_raw else IMAGES_NAME) as f:
        for m in tqdm.tqdm_notebook(f.getmembers()):
            
            if m.isfile() and m.name.endswith(".jpg"):
                
                img = decode_image_from_raw_bytes(f.extractfile(m).read())

                
                img = img(dy:-dy, dx:-dx)
                img = cv2.resize(img, (dimx, dimy))

                
                fname = os.path.split(m.name)(-1)
                fname_splitted = fname(:-4).replace('_', ' ').split()
                person_id = ' '.join(fname_splitted(:-1))
                photo_number = int(fname_splitted(-1))
                if (person_id, photo_number) in imgs_with_attrs:
                    all_photos.append(img)
                    photo_ids.append({'person': person_id, 'imagenum': photo_number})

    photo_ids = pd.DataFrame(photo_ids)
    all_photos = np.stack(all_photos).astype('uint8')

    
    all_attrs = photo_ids.merge(df_attrs, روی=('person', 'imagenum')).drop(("person", "imagenum"), axis=1)

    return all_photos, all_attrs

پیاده سازی Autoencoder

import numpy as np
X, attr = load_lfw_dataset(use_raw=True, dimx=32, dimy=32)

داده های ما در X ماتریس، به شکل یک ماتریس سه بعدی، که نمایش پیش فرض برای تصاویر RGB است. با ارائه سه ماتریس – قرمز، سبز و آبی، ترکیب این سه رنگ تصویر را ایجاد می کند.

این تصاویر برای هر پیکسل مقادیر بزرگی خواهند داشت که از 0 تا 255 متغیر است. معمولاً در یادگیری ماشینی ما تمایل داریم مقادیر را کوچک و حول محور 0 قرار دهیم، زیرا این به مدل ما کمک می‌کند سریع‌تر تمرین کند و نتایج بهتری بگیرد، بنابراین بیایید تصاویر خود را عادی کنیم:

X = X.astype('float32') / 255.0 - 0.5

تا الان اگه تست کنیم X آرایه برای حداقل و حداکثر آن خواهد بود -.5 و .5، که می توانید تأیید کنید:

print(X.max(), X.min())

0.5 -0.5

برای اینکه بتوانیم تصویر را ببینیم، a ایجاد می کنیم show_image تابع. اضافه خواهد کرد 0.5 به تصاویر زیرا مقدار پیکسل نمی تواند منفی باشد:

import matplotlib.pyplot as plt
def show_image(x):
    plt.imshow(np.clip(x + 0.5, 0, 1))

حالا بیایید نگاهی گذرا به داده های خود بیندازیم:

show_image(X(6))

عالی است، اکنون اجازه دهید داده های خود را به یک مجموعه آموزشی و آزمایشی تقسیم کنیم:

from sklearn.model_selection import train_test_split
X_train, X_test = train_test_split(X, test_size=0.1, random_state=42)

را sklearn train_test_split() تابع می‌تواند داده‌ها را با دادن نسبت تست تقسیم کند و بقیه، البته، اندازه آموزش است. را random_state، که در یادگیری ماشینی بسیار مشاهده خواهید کرد، صرف نظر از اینکه کد را چند بار اجرا می کنید، برای ایجاد نتایج یکسان استفاده می شود.

حالا نوبت مدل است:

from keras.layers import Dense, Flatten, Reshape, Input, InputLayer
from keras.models import Sequential, Model

def build_autoencoder(img_shape, code_size):
    
    encoder = Sequential()
    encoder.add(InputLayer(img_shape))
    encoder.add(Flatten())
    encoder.add(Dense(code_size))

    
    decoder = Sequential()
    decoder.add(InputLayer((code_size,)))
    decoder.add(Dense(np.prod(img_shape))) 
    decoder.add(Reshape(img_shape))

    return encoder, decoder

این تابع یک image_shape (ابعاد تصویر) و code_size (اندازه نمایش خروجی) به عنوان پارامتر. شکل تصویر، در مورد ما، خواهد بود (32, 32, 3) جایی که 32 نشان دهنده عرض و ارتفاع و 3 ماتریس های کانال رنگ را نشان می دهد. همانطور که گفته شد، تصویر ما دارد 3072 ابعاد

منطقاً هر چه کوچکتر باشد code_size است، تصویر بیشتر فشرده می شود، اما ویژگی های کمتری ذخیره می شود و تصویر بازتولید شده بسیار متفاوت از اصلی خواهد بود.

یک مدل ترتیبی Keras اساساً برای افزودن متوالی لایه‌ها و عمیق‌تر کردن شبکه استفاده می‌شود. هر لایه به لایه بعدی وارد می شود، و در اینجا، ما به سادگی با لایه شروع می کنیم InputLayer (مکانی برای ورودی) با اندازه بردار ورودی – image_shape.

را Flatten وظیفه لایه صاف کردن آن است (32,32,3) ماتریس به آرایه 1 بعدی (3072) از آنجایی که معماری شبکه ماتریس های سه بعدی را نمی پذیرد.

آخرین لایه در رمزگذار همان است Dense لایه، که در اینجا شبکه عصبی واقعی است. سعی می‌کند پارامترهای بهینه‌ای را پیدا کند که بهترین خروجی را به دست می‌آورد – در مورد ما رمزگذاری است، و اندازه خروجی آن (همچنین تعداد نورون‌های موجود در آن) را روی مقدار تنظیم می‌کنیم. code_size.

رمزگشا نیز یک مدل ترتیبی است. ورودی (رمزگذاری) را می پذیرد و سعی می کند آن را در قالب یک ردیف بازسازی کند. سپس، آن را در یک پشته قرار می دهد 32x32x3 ماتریس از طریق Dense لایه. آخرین Reshape لایه آن را به یک تصویر تغییر شکل می دهد.

حالا بیایید آنها را به هم وصل کنیم و مدل خود را شروع کنیم:

IMG_SHAPE = X.shape(1:)
encoder, decoder = build_autoencoder(IMG_SHAPE, 32)

inp = Input(IMG_SHAPE)
code = encoder(inp)
reconstruction = decoder(code)

autoencoder = Model(inp,reconstruction)
autoencoder.compile(optimizer='adamax', loss='mse')

print(autoencoder.summary())

این کد بسیار ساده است – ما code متغیر خروجی رمزگذار است که آن را در رمزگشا قرار داده و آن را تولید می کنیم reconstruction متغیر.

پس از آن، هر دو را با ایجاد یک پیوند می دهیم Model با inp و reconstruction پارامترها و کامپایل آنها با adamax بهینه ساز و mse عملکرد از دست دادن

تدوین مدل در اینجا به معنای تعریف هدف و روش رسیدن به آن است. هدف در زمینه ما به حداقل رساندن آن است mse و ما با استفاده از یک بهینه ساز به آن می رسیم – که اساساً یک الگوریتم بهینه سازی شده برای یافتن حداقل جهانی است.

در این مرحله می‌توانیم نتایج را خلاصه کنیم:

_________________________________________________________________
Layer (type)                 Output Shape              Param 
=================================================================
input_6 (InputLayer)         (None, 32, 32, 3)         0
_________________________________________________________________
sequential_3 (Sequential)    (None, 32)                98336
_________________________________________________________________
sequential_4 (Sequential)    (None, 32, 32, 3)         101376
=================================================================
Total params: 199,712
Trainable params: 199,712
Non-trainable params: 0
_________________________________________________________________

در اینجا ما می توانیم ورودی را ببینیم 32,32,3. توجه داشته باشید که None در اینجا به شاخص نمونه اشاره می شود، زیرا داده ها را به مدلی که شکلی از آن خواهد داشت می دهیم (m, 32,32,3)، جایی که m تعداد نمونه ها است، بنابراین آن را به عنوان نگه می داریم None.

لایه پنهان است 32، که در واقع اندازه رمزگذاری است که ما انتخاب کردیم، و در نهایت خروجی رمزگشا همانطور که می بینید این است (32,32,3).

حالا بیایید مدل را معامله کنیم:

history = autoencoder.fit(x=X_train, y=X_train, epochs=20,
                validation_data=(X_test, X_test))

در مورد ما، ما تصاویر ساخته شده را با تصاویر اصلی مقایسه خواهیم کرد، بنابراین هر دو x و y برابر هستند X_train. در حالت ایده آل، ورودی برابر با خروجی است.

را epochs متغیر تعریف می‌کند که چند بار می‌خواهیم داده‌های آموزشی از طریق مدل و مدل ارسال شوند validation_data مجموعه اعتبارسنجی است که ما برای ارزیابی مدل بعد از آموزش استفاده می کنیم:

Train روی 11828 samples, validate روی 1315 samples
Epoch 1/20
11828/11828 (==============================) - 3s 272us/step - loss: 0.0128 - val_loss: 0.0087
Epoch 2/20
11828/11828 (==============================) - 3s 227us/step - loss: 0.0078 - val_loss: 0.0071
.
.
.
Epoch 20/20
11828/11828 (==============================) - 3s 237us/step - loss: 0.0067 - val_loss: 0.0066

می‌توانیم زیان را در طول دوره‌ها مجسم کنیم تا یک نمای کلی در مورد تعداد دوره‌ها به دست آوریم.

plt.plot(history.history('loss'))
plt.plot(history.history('val_loss'))
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(('train', 'test'), loc='upper left')
plt.show()

ما می‌توانیم ببینیم که پس از دوره سوم، پیشرفت قابل‌توجهی در از دست دادن وجود ندارد. تجسم مانند این می تواند به شما کمک کند تا ایده بهتری در مورد اینکه چند دوره واقعاً برای آموزش مدل شما کافی است داشته باشید. در این مورد، به سادگی نیازی به آموزش آن نیست 20 دوره ها، و بیشتر آموزش ها اضافی است.

این همچنین می تواند منجر به بیش از حد برازش مدل شود که باعث عملکرد ضعیف آن می شود روی داده های جدید خارج از مجموعه داده های آموزشی و آزمایشی.

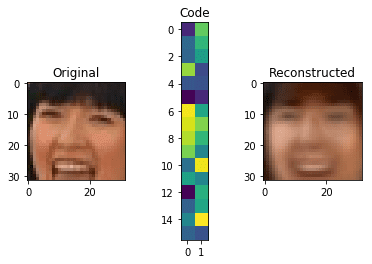
اکنون، مورد انتظارترین بخش – بیایید نتایج را تجسم کنیم:

def visualize(img,encoder,decoder):
    """Draws original, encoded and decoded images"""
    
    code = encoder.predict(img(None))(0)
    reco = decoder.predict(code(None))(0)

    plt.subplot(1,3,1)
    plt.title("Original")
    show_image(img)

    plt.subplot(1,3,2)
    plt.title("Code")
    plt.imshow(code.reshape((code.shape(-1)//2,-1)))

    plt.subplot(1,3,3)
    plt.title("Reconstructed")
    show_image(reco)
    plt.show()

for i in range(5):
    img = X_test(i)
    visualize(img,encoder,decoder)

می بینید که نتایج واقعاً خوب نیستند. با این حال، اگر در نظر بگیریم که کل تصویر در بردار بسیار کوچک کدگذاری شده است 32 این وسط دیده می شود، این اصلاً بد نیست. از طریق فشرده سازی از 3072 ابعاد فقط 32 ما داده های زیادی را از دست می دهیم

حالا بیایید مقدار را افزایش دهیم code_size به 1000:

تفاوت را ببین؟ همانطور که به مدل فضای بیشتری برای کار می دهید، اطلاعات مهم تری در مورد تصویر ذخیره می شود

توجه داشته باشید: همانطور که در بالا نشان داده شد، رمزگذاری دو بعدی نیست. این فقط برای اهداف تصویری است. در واقع، این یک آرایه یک بعدی از 1000 بعد است.

کاری که ما انجام دادیم نام دارد تجزیه و تحلیل مؤلفه های اصلی (PCA)، که یک کاهش ابعاد تکنیک. می‌توانیم از آن برای کاهش اندازه مجموعه ویژگی‌ها با ایجاد ویژگی‌های جدید که اندازه کوچک‌تر هستند، اما همچنان اطلاعات مهم را ضبط می‌کنند، استفاده کنیم.

تجزیه و تحلیل مؤلفه اصلی استفاده بسیار محبوبی از رمزگذارهای خودکار است.

حذف نویز تصویر

یکی دیگر از کاربردهای محبوب رمزگذارهای خودکار، حذف نویز است. بیایید مقداری نویز تصادفی به تصاویر خود اضافه کنیم:

def apply_gaussian_noise(X, sigma=0.1):
    noise = np.random.normal(loc=0.0, scale=sigma, size=X.shape)
    return X + noise

در اینجا مقداری نویز تصادفی از توزیع نرمال استاندارد با مقیاس اضافه می کنیم sigma، که پیش فرض است 0.1.

برای مرجع، این همان چیزی است که نویز با موارد مختلف به نظر می رسد sigma ارزش های:

plt.subplot(1,4,1)
show_image(X_train(0))
plt.subplot(1,4,2)
show_image(apply_gaussian_noise(X_train(:1),sigma=0.01)(0))
plt.subplot(1,4,3)
show_image(apply_gaussian_noise(X_train(:1),sigma=0.1)(0))
plt.subplot(1,4,4)
show_image(apply_gaussian_noise(X_train(:1),sigma=0.5)(0))

همانطور که می بینیم، به عنوان sigma افزایش می یابد به 0.5 تصویر به سختی دیده می شود ما سعی خواهیم کرد تصویر اصلی را با یک سیگما از تصاویر نویزدار بازسازی کنیم 0.1.

مدلی که ما برای این کار تولید خواهیم کرد مانند مدل قبلی است، اگرچه آن را متفاوت آموزش خواهیم داد. این بار، ما آن را با تصاویر نویز اصلی و متناظر آموزش خواهیم داد:

code_size = 100


encoder, decoder = build_autoencoder(IMG_SHAPE, code_size=code_size)

inp = Input(IMG_SHAPE)
code = encoder(inp)
reconstruction = decoder(code)

autoencoder = Model(inp, reconstruction)
autoencoder.compile('adamax', 'mse')

for i in range(25):
    print("Epoch %i/25, Generating corrupted samples..."%(i+1))
    X_train_noise = apply_gaussian_noise(X_train)
    X_test_noise = apply_gaussian_noise(X_test)

    
    autoencoder.fit(x=X_train_noise, y=X_train, epochs=1,
                    validation_data=(X_test_noise, X_test))

حالا بیایید نتایج مدل را ببینیم:

X_test_noise = apply_gaussian_noise(X_test)
for i in range(5):
    img = X_test_noise(i)
    visualize(img,encoder,decoder)

برنامه های Autoencoder

علاوه بر مواردی که تاکنون بررسی کرده ایم، کاربردهای بیشتری برای رمزگذارهای خودکار وجود دارد.

Autoencoder را می توان در برنامه هایی مانند دیپ فیک، جایی که شما یک رمزگذار و رمزگشا از مدل های مختلف دارید.

به عنوان مثال، فرض کنید دو رمزگذار خودکار برای آن داریم Person X و یکی برای Person Y. هیچ چیز ما را از استفاده از رمزگذار باز نمی دارد Person X و رمزگشا از Person Y و سپس تصاویری از Person Y با ویژگی های بارز Person X:

اعتبار: آلن زوکونی

رمزگذارهای خودکار همچنین می‌توانند برای تقسیم‌بندی تصویر استفاده شوند – مانند وسایل نقلیه خودمختار که در آن باید موارد مختلفی را برای خودرو تقسیم کنید تا تصمیم بگیرید:

اعتبار: PapersWithCode

نتیجه

رمزگذارهای خودکار را می توان برای تجزیه و تحلیل اجزای اصلی استفاده کرد که یک تکنیک کاهش ابعاد، حذف نویز تصویر و موارد دیگر است.

می توانید خودتان آن را با مجموعه داده های مختلف امتحان کنید، مانند مثال MNIST مجموعه داده و ببینید چه نتایجی به دست می آورید.