از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
محاسبه ضریب همبستگی پیرسون در پایتون با Numpy
سرفصلهای مطلب
معرفی
این مقاله مقدمه ای است برای ضریب همبستگی پیرسون، محاسبه دستی آن و محاسبه آن از طریق پایتون numpy مدول.
ضریب همبستگی پیرسون اندازه گیری می شود ارتباط خطی بین متغیرها مقدار آن را می توان اینگونه تفسیر کرد:
- +1 – همبستگی مثبت کامل
- +0.8 – همبستگی مثبت قوی
- +0.6 – همبستگی مثبت متوسط
- 0 – هیچ ارتباطی وجود ندارد
- -0.6 – همبستگی منفی متوسط
- -0.8 – همبستگی منفی قوی
- -1 – همبستگی منفی کامل
ما نشان خواهیم داد که چگونه ضریب همبستگی با انواع مختلف ارتباط متفاوت است. در این مقاله، ما آن را نیز نشان خواهیم داد همبستگی صفر همیشه به این معنی نیست هیچ ارتباطی. متغیرهای غیر خطی مرتبط ممکن است ضرایب همبستگی نزدیک به صفر داشته باشند.
ضریب همبستگی پیرسون چیست؟
ضریب همبستگی پیرسون نیز به نام ضریب همبستگی محصول-لحظه پیرسون. این معیاری از رابطه خطی بین دو متغیر تصادفی است – ایکس و Y. از نظر ریاضی اگر (σXY) کوواریانس بین است ایکس و Y، و (σX) انحراف معیار است ایکس، سپس ضریب همبستگی پیرسون ρ از رابطه زیر بدست می آید:
$$
\rho_{X,Y} = \frac{\sigma_{XY}}{\sigma_X \sigma_Y}
$$
از آنجایی که کوواریانس همیشه کوچکتر از حاصل ضرب انحرافات استاندارد فردی است، مقدار ρ بین -1 و +1. از موارد بالا همچنین می توان دریافت که همبستگی یک متغیر با خودش یک است:
$$
\rho_{X,X} = \frac{\sigma_{XX}}{\sigma_X \sigma_X} = 1
$$
قبل از شروع کدنویسی، یک مثال کوتاه می زنیم تا ببینیم این ضریب چگونه محاسبه می شود.
ضریب همبستگی پیرسون چگونه محاسبه می شود؟
فرض کنید مشاهداتی از متغیرهای تصادفی به ما داده شده است ایکس و Y. اگر قصد دارید همه چیز را از ابتدا پیاده سازی کنید یا محاسبات دستی انجام دهید، در صورت ارائه به موارد زیر نیاز دارید ایکس و Y:
بیایید از موارد بالا برای محاسبه همبستگی استفاده کنیم. ما از تخمین سوگیری کوواریانس و انحرافات استاندارد استفاده خواهیم کرد. این امر بر مقدار ضریب همبستگی که محاسبه می شود تأثیر نمی گذارد زیرا تعداد مشاهدات در صورت و مخرج لغو می شود:
ضریب همبستگی پیرسون در استفاده از پایتون NumPy
ضریب همبستگی پیرسون را می توان در پایتون با استفاده از corrcoef() روش از NumPy.
ورودی این تابع معمولاً یک ماتریس است، مثلاً اندازه mxn، جایی که:
- هر ستون نشان دهنده مقادیر یک متغیر تصادفی است
- هر ردیف نشان دهنده یک نمونه واحد از
nمتغیرهای تصادفی nتعداد کل متغیرهای تصادفی مختلف را نشان می دهدmتعداد کل نمونه ها برای هر متغیر را نشان می دهد
برای n متغیرهای تصادفی، an را برمی گرداند nxn ماتریس مربع M، با M(i,j) نشان دهنده ضریب همبستگی بین متغیر تصادفی است i و j. از آنجایی که ضریب همبستگی بین یک متغیر و خودش 1 است، تمام ورودی های مورب (i,i) برابر با یک هستند.
به اختصار:
توجه داشته باشید که ماتریس همبستگی متقارن است همانطور که همبستگی متقارن است، به عنوان مثال، M(i,j) = M(j,i). بیایید مثال ساده خود را از بخش قبل بگیریم و روش استفاده را ببینیم corrcoef() با numpy.
اول، اجازه دهید import را numpy ماژول، در کنار pyplot ماژول از Matplotlib. بعداً از Matplotlib برای تجسم همبستگی استفاده خواهیم کرد روی:
import numpy as np
import matplotlib.pyplot as plt
ما از همان مقادیر مثال دستی قبلی استفاده خواهیم کرد. بیایید آن را در آن ذخیره کنیم x_simple و ماتریس همبستگی را محاسبه کنید:
x_simple = np.array((-2, -1, 0, 1, 2))
y_simple = np.array((4, 1, 3, 2, 0))
my_rho = np.corrcoef(x_simple, y_simple)
print(my_rho)
در زیر ماتریس همبستگی خروجی آمده است. به آنها توجه کنید روی قطرها، نشان می دهد که ضریب همبستگی یک متغیر با خودش یک است:
(( 1. -0.7)
(-0.7 1. ))
مثال های همبستگی مثبت و منفی
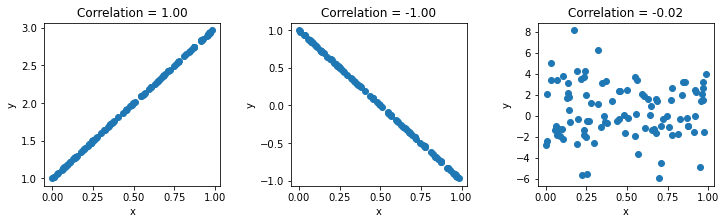
بیایید ضرایب همبستگی را برای چند رابطه مجسم کنیم. اول، ما یک مثبت کامل (+1) و منفی کامل (-1) همبستگی بین دو متغیر. سپس، دو متغیر تصادفی تولید میکنیم، بنابراین ضریب همبستگی باید تقریباً نزدیک به صفر باشد، مگر اینکه تصادفی بودن تصادفی دارای همبستگی باشد، که بسیار بعید است.
ما از a استفاده خواهیم کرد seed به طوری که این مثال در هنگام فراخوانی قابل تکرار باشد RandomState از NumPy:
seed = 13
rand = np.random.RandomState(seed)
x = rand.uniform(0,1,100)
x = np.vstack((x,x*2+1))
x = np.vstack((x,-x(0,)*2+1))
x = np.vstack((x,rand.normal(1,3,100)))
اولین rand.uniform() فراخوانی یک توزیع یکنواخت تصادفی ایجاد می کند:
(7.77702411e-01 2.37541220e-01 8.24278533e-01 9.65749198e-01
9.72601114e-01 4.53449247e-01 6.09042463e-01 7.75526515e-01
6.41613345e-01 7.22018230e-01 3.50365241e-02 2.98449471e-01
5.85124919e-02 8.57060943e-01 3.72854028e-01 6.79847952e-01
2.56279949e-01 3.47581215e-01 9.41277008e-03 3.58333783e-01
9.49094182e-01 2.17899009e-01 3.19391366e-01 9.17772386e-01
3.19036664e-02 6.50845370e-02 6.29828999e-01 8.73813443e-01
8.71573230e-03 7.46577237e-01 8.12841171e-01 7.57174462e-02
6.56455335e-01 5.09262200e-01 4.79883391e-01 9.55574145e-01
1.20335695e-05 2.46978701e-01 7.12232678e-01 3.24582050e-01
2.76996356e-01 6.95445453e-01 9.18551748e-01 2.44475702e-01
4.58085817e-01 2.52992683e-01 3.79333291e-01 6.04538829e-01
7.72378760e-01 6.79174968e-02 6.86085079e-01 5.48260097e-01
1.37986053e-01 9.87532192e-02 2.45559105e-01 1.51786663e-01
9.25994479e-01 6.80105016e-01 2.37658922e-01 5.68885253e-01
5.56632051e-01 7.27372109e-02 8.39708510e-01 4.05319493e-01
1.44870989e-01 1.90920059e-01 4.90640137e-01 7.11403374e-01
9.84938458e-01 8.74786502e-01 4.99041684e-01 1.06779994e-01
9.13212807e-01 3.64915961e-01 2.26587877e-01 8.72431862e-01
1.36358352e-01 2.36380160e-01 5.95399245e-01 5.63922609e-01
9.58934732e-01 4.53239333e-01 1.28958075e-01 7.60567677e-01
2.01634075e-01 1.75729863e-01 4.37118013e-01 3.40260803e-01
9.67253109e-01 1.43026077e-01 8.44558533e-01 6.69406140e-01
1.09304908e-01 8.82535400e-02 9.66462041e-01 1.94297485e-01
8.19000600e-02 2.69384695e-01 6.50130518e-01 5.46777245e-01)
سپس، می توانیم تماس بگیریم vstack() تا آرایه های دیگر را به صورت عمودی روی آن قرار دهید. به این ترتیب، ما میتوانیم دستهای از متغیرها را مانند متغیرهای بالا در همان دسته قرار دهیم x به آنها مراجعه کرده و به ترتیب به آنها دسترسی داشته باشید.
پس از اولین توزیع یکنواخت، ما چند مجموعه متغیر را به صورت عمودی روی هم چیده ایم – مجموعه دوم دارای رابطه مثبت کامل با اولی، سومی دارای همبستگی منفی کامل با اولین، و چهارمی کاملا تصادفی است. بنابراین باید همبستگی ~0 داشته باشد.
وقتی مجرد داریم x مرجعی مانند این، میتوانیم همبستگی را برای هر یک از عناصر در پشته عمودی با ارسال آن به تنهایی محاسبه کنیم np.corrcoef():
rho = np.corrcoef(x)
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(12, 3))
for i in (0,1,2):
ax(i).scatter(x(0,),x(1+i,))
ax(i).title.set_text('Correlation = ' + "{:.2f}".format(rho(0,i+1)))
ax(i).set(xlabel='x',ylabel='y')
fig.subplots_adjust(wspace=.4)
plt.show()

درک تغییرات ضریب همبستگی پیرسون
فقط برای اینکه ببینیم ضریب همبستگی با تغییر در رابطه بین دو متغیر چگونه تغییر می کند، اجازه دهید مقداری نویز تصادفی به آن اضافه کنیم. x ماتریس در بخش قبل ایجاد شده و کد را دوباره اجرا کنید.
در این مثال، ما به آرامی درجات مختلفی از نویز را به نمودارهای همبستگی اضافه می کنیم و ضرایب همبستگی را محاسبه می کنیم. روی هر مرحله:
fig, ax = plt.subplots(nrows=2, ncols=4, figsize=(15, 8))
for noise, i in zip((0.05,0.2,0.8,2),(0,1,2,3)):
x_with_noise = x+rand.normal(0,noise,x.shape)
rho_noise = np.corrcoef(x_with_noise)
ax(0,i).scatter(x_with_noise(0,),x_with_noise(1,),color='magenta')
ax(1,i).scatter(x_with_noise(0,),x_with_noise(2,),color='green')
ax(0,i).title.set_text('Correlation = ' + "{:.2f}".format(rho_noise(0,1))
+ '\n Noise = ' + "{:.2f}".format(noise) )
ax(1,i).title.set_text('Correlation = ' + "{:.2f}".format(rho_noise(0,2))
+ '\n Noise = ' + "{:.2f}".format(noise))
ax(0,i).set(xlabel='x',ylabel='y')
ax(1,i).set(xlabel='x',ylabel='y')
fig.subplots_adjust(wspace=0.3,hspace=0.4)
plt.show()

یک دام رایج: ارتباط بدون همبستگی
یک تصور غلط رایج وجود دارد که همبستگی صفر به معنای عدم ارتباط است. بیایید روشن کنیم که همبستگی دقیقاً اندازه گیری می کند رابطه خطی بین دو متغیر
مثال های زیر متغیرهایی را نشان می دهد که به صورت غیر خطی با یکدیگر مرتبط هستند اما همبستگی صفر دارند.
آخرین مثال از (y=eایکس) دارای ضریب همبستگی حدود 0.52 است که بازتابی از ارتباط واقعی بین دو متغیر نیست:
x_nonlinear = np.linspace(-10,10,100)
x_nonlinear = np.vstack((x_nonlinear,x_nonlinear*x_nonlinear))
x_nonlinear = np.vstack((x_nonlinear,-x_nonlinear(0,)**2))
x_nonlinear = np.vstack((x_nonlinear,x_nonlinear(0,)**4))
x_nonlinear = np.vstack((x_nonlinear,np.log(x_nonlinear(0,)**2+1)))
x_nonlinear = np.vstack((x_nonlinear,np.exp(x_nonlinear(0,))))
rho_nonlinear = np.corrcoef(x_nonlinear)
fig, ax = plt.subplots(nrows=1, ncols=5, figsize=(16, 3))
title = ('$y=x^2$','$y=-x^2$','$y=x^4$','$y=\log(x^2+1)$','$y=\exp(x)$')
for i in (0,1,2,3,4):
ax(i).scatter(x_nonlinear(0,),x_nonlinear(1+i,),color='cyan')
ax(i).title.set_text(title(i) + '\n' +
'Correlation = ' + "{:.2f}".format(rho_nonlinear(0,i+1)))
ax(i).set(xlabel='x',ylabel='y')
fig.subplots_adjust(wspace=.4)
plt.show()

نتیجه گیری
در این مقاله به ضریب همبستگی پیرسون پرداختیم. ما استفاده کردیم corrcoef() روش از پایتون numpy ماژول برای محاسبه مقدار آن
اگر متغیرهای تصادفی دارای ارتباط خطی بالایی باشند، ضریب همبستگی آنها نزدیک به 1+ یا 1- است. از سوی دیگر، متغیرهای مستقل آماری دارای ضرایب همبستگی نزدیک به صفر هستند.
ما همچنین نشان دادیم که انجمنهای غیرخطی میتوانند ضریب همبستگی صفر یا نزدیک به صفر داشته باشند، به این معنی که متغیرهایی که ارتباط بالایی دارند ممکن است مقدار بالایی از ضریب همبستگی پیرسون نداشته باشند.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-13 21:58:04



