از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
محاسبه فاصله اقلیدسی با NumPy
سرفصلهای مطلب
در این راهنما – ما نگاهی به روش محاسبه فاصله اقلیدسی بین دو نقطه در پایتون با استفاده از Numpy.
فاصله اقلیدسی چیست؟
فاصله اقلیدسی یک متریک اساسی فاصله مربوط به سیستم های داخل است فضای اقلیدسی.
فضای اقلیدسی است فضای هندسی کلاسیک که در کلاس ریاضی با آن آشنا می شوید، معمولاً به 3 بعد محدود می شود. اگرچه، می توان آن را برای هر بعد عدد صحیح غیر منفی نیز تجویز کرد.
فاصله اقلیدسی کوتاهترین خط بین دو نقطه در فضای اقلیدسی است.
این نام از اقلیدس گرفته شده است که به طور گسترده ای به عنوان شناخته شده است “پدر هندسه”، زیرا این تنها فضایی بود که مردم آن زمان معمولاً آن را تصور می کردند. در طول زمان، انواع مختلفی از فضا در فیزیک و ریاضیات مشاهده شده است، مانند فضای Affineو فضاهای غیر اقلیدسی و هندسه برای ادراک شناختی ما بسیار غیر شهودی هستند.
در فضای اقلیدسی سه بعدی، کوتاهترین خط بین دو نقطه خواهد بود همیشه یک خط مستقیم باشید بین آنها، اگرچه این برای ابعاد بالاتر صدق نمی کند.
با توجه به این واقعیت، فاصله اقلیدسی همیشه مفیدترین معیار برای پیگیری در برخورد با ابعاد مختلف نیست و ما تمرکز خواهیم کرد. روی فضای اقلیدسی دو بعدی و سه بعدی برای محاسبه فاصله اقلیدسی.
اندازه گیری فاصله برای داده های با ابعاد بالا معمولاً با سایر معیارهای فاصله مانند انجام می شود فاصله منهتن.
به طور کلی، فاصله اقلیدسی دارد عمده استفاده در توسعه جهان های سه بعدی و همچنین الگوریتم های یادگیری ماشین که شامل معیارهای فاصله است، مانند K-Nearest Neighbors. به طور معمول، فاصله اقلیدسی نشان می دهد که دو نقطه داده چقدر شبیه به یکدیگر هستند – با فرض برخی از خوشه بندی ها روی داده های دیگر قبلاً انجام شده است.
فرمول ریاضی
فرمول ریاضی برای محاسبه فاصله اقلیدسی بین 2 نقطه در فضای دو بعدی:
$$
d(p,q) = \sqrt(2){(q_1-p_1)^2 + (q_2-p_2)^2 }
$$
این فرمول به راحتی با فضای سه بعدی و همچنین هر ابعادی سازگار است:
$$
d(p,q) = \sqrt(2){(q_1-p_1)^2 + (q_2-p_2)^2 + (q_3-p_3)^2 }
$$
فرمول کلی را می توان به صورت زیر ساده کرد:
$$
d(p,q) = \sqrt(2){(q_1-p_1)^2 + … + (q_n-p_n)^2 }
$$
یک چشم تیزبین ممکن است متوجه شباهت بین فاصله اقلیدسی و قضیه فیثاغورث شود:
$$
C^2 = A^2 + B^2
$$
$$
d(p,q)^2 = (q_1-p_1)^2 + (q_2-p_2)^2
$$
در واقع وجود دارد است یک رابطه بین اینها – فاصله اقلیدسی از طریق قضیه فیثاغورث با توجه به مختصات دکارتی دو نقطه محاسبه می شود.
به خاطر همین، فاصله اقلیدسی گاهی اوقات به عنوان شناخته می شود فاصله فیثاغورثو همچنین، با این حال، نام قبلی بسیار بیشتر شناخته شده است.
توجه داشته باشید: دو نقطه بردار هستند، اما خروجی باید اسکالر باشد (که فاصله است).
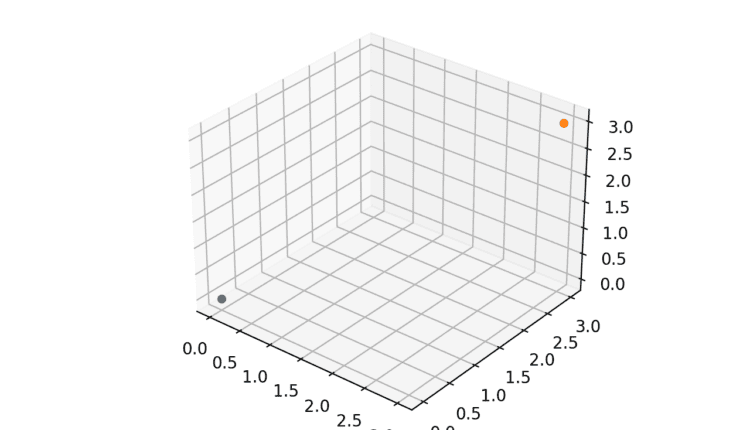
ما از NumPy برای محاسبه این فاصله برای دو نقطه استفاده خواهیم کرد و همین رویکرد برای فضاهای دو بعدی و سه بعدی استفاده می شود:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
ax.scatter(0, 0, 0)
ax.scatter(3, 3, 3)
plt.show()

محاسبه فاصله اقلیدسی در پایتون با NumPy
ابتدا باید کتابخانه NumPy را نصب کنیم:
$ pip install numpy
حالا وقته import و دو نقطه خود را با مختصات دکارتی به صورت (0، 0، 0) و (3، 3، 3) تنظیم کنید:
import numpy as np
point_1 = np.array((0, 0, 0))
point_2 = np.array((3, 3, 3))
اکنون، به جای اینکه محاسبه را به صورت دستی انجام دهیم، از روش های کمکی NumPy برای آسان تر کردن این کار استفاده کنیم!
np.sqrt() و np.sum()
عملیات و توابع ریاضی مورد نیاز برای محاسبه فاصله اقلیدسی بسیار ساده است: علاوه بر این، منها کردن، به همان خوبی مربع root تابع. افزودن های متعدد را می توان با a جایگزین کرد مجموع، همچنین:
$$
d(p,q) = \sqrt(2){(q_1-p_1)^2 + (q_2-p_2)^2 + (q_3-p_3)^2 }
$$
NumPy به ما یک np.sqrt() تابع، نشان دهنده مربع است root عملکرد، و همچنین یک np.sum() تابع، که یک جمع را نشان می دهد. با این موارد، محاسبه فاصله اقلیدسی در پایتون ساده و شهودی است:
square = np.square(point_1 - point_2)
sum_square = np.sum(square)
این یک نتیجه بسیار ساده به ما می دهد:
(0-3)^2 + (0-3)^2 + (0-3)^2
که برابر است با 27. تنها چیزی که باقی می ماند بدست آوردن مربع است root از آن عدد:
distance = np.sqrt(sum_square)
print(distance)
این نتیجه در:
5.196152422706632
در روح واقعی پایتونیک، این می تواند تنها به یک خط کوتاه شود:
distance = np.sqrt(np.sum(np.square(point_1 - point_2)))
و حتی می توانید از داخلی استفاده کنید pow() و sum() روش های math در عوض ماژول پایتون، هر چند آنها از شما می خواهند که کمی با ورودی هک کنید، که به راحتی با استفاده از NumPy انتزاع می شود. pow() تابع فقط با اسکالرها کار می کند (هر عنصر در آرایه به صورت جداگانه) و یک آرگومان را می پذیرد – عدد را به چه قدرتی افزایش می دهید.
این رویکرد، هر چند، به طور شهودی به نظر می رسد بیشتر شبیه فرمولی که قبلاً استفاده کرده ایم:
from math import *
distance = np.sqrt(sum(pow(a-b, 2) for a, b in zip(point_1, point_2)))
print(distance)
این نیز منجر به:
5.196152422706632
np.linalg.norm()
این np.linalg.norm() تابع نشان دهنده a است هنجار ریاضی. در اصل ، الف هنجار از یک بردار آن است طول. این طول لزوماً لازم نیست فاصله اقلیدسی، و می تواند مسافت های دیگری نیز باشد. فاصله اقلیدسی است هنجار L2 یک بردار (گاهی اوقات به عنوان هنجار اقلیدسی) و به طور پیش فرض ، norm() تابع از L2 استفاده می کند – ord پارامتر روی 2 تنظیم شده است.
اگر قرار بود تنظیم کنید ord پارامتر به مقداری دیگر پ، شما دیگر را محاسبه می کنید کرم های P. به عنوان مثال، L1 هنجار یک بردار فاصله منهتن است!
با توجه به این ، ما می توانیم از np.linalg.norm() تابعی برای محاسبه فاصله اقلیدسی به راحتی و بسیار تمیزتر از استفاده از سایر توابع:
distance = np.linalg.norm(point_1-point_2)
print(distance)
این منجر به چاپ فاصله L2/اقلیدسی می شود:
5.196152422706632
عادی سازی L2 و عادی سازی L1 به شدت در یادگیری ماشین برای عادی سازی داده های ورودی استفاده می شود.
اگر میخواهید درباره مقیاسبندی ویژگیها بیشتر بدانید – راهنمای ما برای دادههای مقیاسبندی ویژگی با Scikit-Learn را بخوانید!
np.dot ()
همچنین می توانیم از a استفاده کنیم نقطه محصول برای محاسبه فاصله اقلیدسی در ریاضیات، محصول نقطه ای نتیجه ضرب دو بردار با طول مساوی است و نتیجه یک عدد واحد است – یک مقدار اسکالر. به دلیل نوع برگشتی، گاهی اوقات به عنوان a نیز شناخته می شود “حاصلضرب عددی”. این عملیات اغلب نامیده می شود محصول داخلی برای دو بردار
برای محاسبه حاصل ضرب نقطه بین 2 بردار می توانید از فرمول زیر استفاده کنید:
$$
\vec{p} \cdot \vec{q} = {(q_1-p_1) + (q_2-p_2) + (q_3-p_3) }
$$
با NumPy می توانیم از آن استفاده کنیم np.dot() تابع، عبور در دو بردار.
اگر ما یک محصول نقطه ای از تفاوت بین هر دو نقطه را با همان تفاوت محاسبه کنیم – عددی به دست می آید که با فاصله اقلیدسی بین آن دو بردار رابطه دارد. استخراج مربع root از آن عدد، مسافتی را که در جستجوی آن هستیم، مشخص می کند:
diff = point_1 - point_2
sum_square = np.dot(diff, diff)
distance = np.sqrt(sum_square)
print(distance)
البته، شما می توانید این را به یک خط نیز کوتاه کنید:
distance = np.sqrt(np.dot(point_1-point_2, point_1-point_2))
print(distance)
5.196152422706632
با استفاده از توکار math.dist()
پایتون روش داخلی خود را دارد، در math ماژول، که فاصله بین 2 نقطه را در فضای 3 بعدی محاسبه می کند. با این حال، این فقط با پایتون 3.8 یا بالاتر کار می کند.
math.dist() دو پارامتر که دو نقطه هستند را می گیرد و فاصله اقلیدسی بین آن نقاط را برمی گرداند.
توجه داشته باشید: لطفا توجه داشته باشید که دو نقطه باید ابعاد یکسانی داشته باشند (یعنی هر دو در فضای 2d یا 3d).
اکنون، برای محاسبه فاصله اقلیدسی بین این دو نقطه، فقط آنها را در آن می اندازیم dist() روش:
import math
distance = math.dist(point_1, point_2)
print(distance)
5.196152422706632
نتیجه
فاصله اقلیدسی یک متریک اساسی فاصله مربوط به سیستم های داخل است فضای اقلیدسی.
فضای اقلیدسی است فضای هندسی کلاسیک که در کلاس ریاضی با آن آشنا می شوید، معمولاً به 3 بعد محدود می شود. اگرچه، می توان آن را برای هر بعد عدد صحیح غیر منفی نیز تجویز کرد.
فاصله اقلیدسی کوتاهترین خط بین دو نقطه در فضای اقلیدسی است.
این معیار در بسیاری از زمینه ها در داده کاوی، یادگیری ماشین و چندین زمینه دیگر استفاده می شود و یکی از معیارهای اساسی فاصله است.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-08 16:13:04



