مرتب سازی رادیکس در پایتون

معرفی

ریشه (یا پایه) است تعداد ارقام برای نمایش اعداد در a استفاده می شود سیستم اعداد موقعیتی. برای سیستم باینری، ریشه است 2 (فقط از دو رقم استفاده می کند – 0 و 1). برای سیستم اعشاری، ریشه است 10 (از ده رقم برای نشان دادن همه اعداد – از 0 تا 9 استفاده می کند).

یک سیستم اعداد موقعیتی، به زبان ساده، یک سیستم نوشتن اعداد است که وزن (یا مقدار) یک رقم با موقعیت آن تعیین می شود. مثلا در شماره 123، 1 ارزش بیشتری دارد 3 زیرا در موقعیتی قرار دارد که نشان دهنده صدها است و 2 در ده است.

مرتب سازی ریشه می تواند برای مرتب سازی واژگانی بسیاری از انواع داده ها – اعداد صحیح، کلمات، ایمیل ها استفاده شود، اما عمدتاً برای مرتب سازی مجموعه هایی از اعداد صحیح و رشته های (که به کلیدهای عدد صحیح مناسب نگاشت می شوند).

این یک الگوریتم مرتب‌سازی غیرمقایسه‌ای است، به این معنی که مجموعه‌ای را با مقایسه عناصر جداگانه آن مرتب نمی‌کند، بلکه از ماهیت ذاتی داده‌هایی که مرتب‌سازی می‌کند برای مرتب‌سازی سریع‌تر استفاده می‌کند – داده‌ها را براساس داده‌ها مرتب می‌کند. روی آنها ریشه.

الگوریتم های مرتب سازی مقایسه ای دارای بهترین پیچیدگی زمانی هستند O(nlogn)، که نسبتاً بدتر از زمان اجرای خطی (O(n+k)) از الگوریتم های غیر مقایسه ای.

به عنوان مثال، اجازه دهید n تعداد عناصری باشد که باید مرتب شوند، و k محدوده مقادیر مجاز عنصر است.

مرتب سازی شمارش (یک الگوریتم غیر مقایسه ای محبوب) دارای پیچیدگی است O(n+k) وقتی که k در محدوده است 1..n. اما، اگر عناصر از 1..n²، سپس پیچیدگی افزایش می یابد O(n²)، که بدتر از هر الگوریتم مرتب سازی مقایسه ای است.

Sort Count پتانسیل به طور قابل توجهی سریعتر از سایر الگوریتم های مقایسه ای رایج است، هرچند، تنها در صورتی که شرط خاصی برآورده شود.

ایده مرتب سازی Radix این است که مرتب سازی شمارش را ارتقا دهید تا پیچیدگی زمانی خطی را حفظ کند حتی اگر دامنه مقادیر عناصر به شدت از تعداد عناصر بیشتر باشد.

در حقیقت، مرتب سازی ریشه ذاتاً استفاده می کند مرتب سازی شمارش به عنوان زیرروال اصلی، با چند ترفند برای غلبه بر مشکلاتی که با افزایش دامنه مقادیر عناصر ایجاد می شود.

الگوریتم مرتب سازی شمارش

برای اینکه بتوانیم مرتب‌سازی رادیکس را درک کنیم، ابتدا باید به مرتب‌سازی شمارش بپردازیم، آن را پیاده‌سازی کنیم و با افزایش تعداد عناصر، سقوط را مشاهده کنیم.

چرا از مرتب سازی شمارش در مرتب سازی رادیکس استفاده کنیم؟

شمارش مرتب سازی پایدار، غیر تطبیقی الگوریتم مرتب سازی، و عمدتا برای مرتب سازی آرایه های عدد صحیح استفاده می شود. همه این ویژگی ها برای استفاده از آن در Radix Sort مهم هستند. شما می توان از الگوریتم‌های دیگر به عنوان زیربرنامه استفاده کنید، تا زمانی که این ویژگی‌ها را داشته باشند، هرچند، مرتب‌سازی شمارش طبیعی‌ترین تطابق است.

مرتب‌سازی رادیکس نیاز به حفظ ترتیب نسبی عناصر با مقادیر کلیدی یکسان در آرایه ورودی دارد، در حالی که ارقام ارزش مکانی یکسان را مرتب می‌کند، بنابراین، زیربرنامه اصلی ما طبق تعریف باید نوعی باشد. الگوریتم مرتب سازی پایدار:

الگوریتم های مرتب سازی غیر مقایسه ای به طور کلی پیچیدگی خطی دارند، بنابراین تأثیر کمتری خواهند داشت روی پیچیدگی مرتب سازی Radix.

مرتب سازی شمارش چگونه کار می کند؟

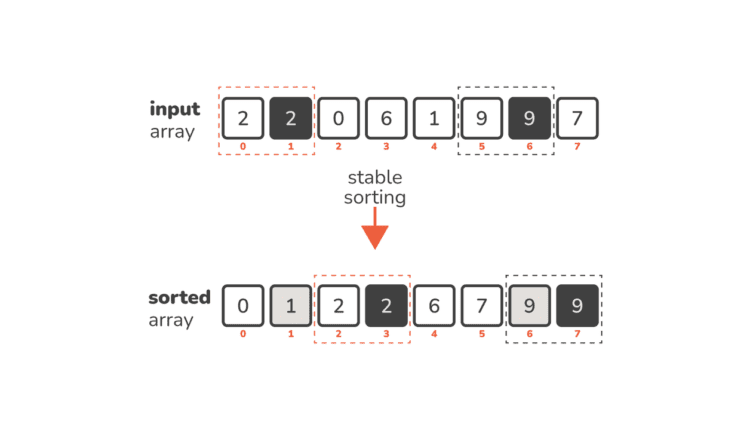
بیایید نگاهی به یک آرایه عدد صحیح مرتب‌نشده بیندازیم که با استفاده از مرتب‌سازی شمارش مرتب‌سازی می‌کنیم:

I = (2, 2, 0, 6, 1, 9, 9, 7)

شمارش مرتب سازی بر اساس شمارش تعداد عناصر، که متناسب است مقدار کلیدی متمایز، و سپس موقعیت های هر کلید را محاسبه می کند.

اول از همه، ما حداکثر عنصر را در آرایه ورودی پیدا خواهیم کرد – max = 9.

سپس، یک آرایه کمکی با آن ایجاد می کنیم max+1 عناصر. این است آرایه شمارش (C) که برای ذخیره تعداد دفعات هر عنصر در آرایه ورودی.

در ابتدا، همه شمارش ها به 0 مقداردهی می شوند:

C = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0) 

حال باید مراحل زیر را طی کنیم:

1. عبور از آرایه ورودی و تعداد مربوط به هر عنصر را افزایش دهید 1

به عنوان مثال، اگر به عنصری با مقدار آن برخورد کنیم 2 در آرایه ورودی (I، 1 را به عنصر با شاخص اضافه می کنیم 2 در آرایه شمارش:

I = (2, 2, 0, 6, 1, 9, 9, 7) 
     ^
        
C = (0, 0, 1, 0, 0, 0, 0, 0, 0, 0) 

پس از این مرحله، آرایه شمارش تعداد دفعات هر عنصر را در قسمت ذخیره می کند آرایه ورودی:

C = (1, 1, 2, 0, 0, 0, 1, 1, 0, 2) 

   

2. برای هر عنصر در آرایه شمارش، مقدار آن را با مقدار تمام عناصر قبلی آن خلاصه کنید و سپس آن مقدار را به عنوان مقدار عنصر فعلی ذخیره کنید:

C = (1, 2, 4, 4, 4, 4, 5, 6, 6, 8) 

به این ترتیب، ما جمع تجمعی عناصر را ذخیره می کنیم آرایه شمارش، روی هر مرحله

3. محاسبه موقعیت عنصر بر اساس روی را آرایه شمارش ارزش های

برای ذخیره این توالی مرتب شده، باید یک آرایه جدید ایجاد کنیم. بیایید اسمش را بگذاریم آرایه خروجی (O) و آن را با مقداردهی اولیه کنید k صفر، کجا k تعداد عناصر موجود در آرایه ورودی:

O = (0, 0, 0, 0, 0, 0, 0, 0) // Initialized output array

برای هر عنصر I(i) (شروع از انتها) در آرایه ورودی:

1. شاخص را در آرایه شمارش که برابر با مقدار عنصر فعلی است I(i)
   • این عنصر است C(j) جایی که j=I(i)
2. تفریق کردن 1 از ارزش C(i)
   • اکنون داریم newValue = C(i)-1
3. ذخیره کنید I(i) به O(newValue)
4. را به روز کنید C(i) با newValue

در پایان، آرایه خروجی شامل عناصر مرتب شده آرایه ورودی است!

پیاده سازی مرتب سازی شمارش در پایتون

حالا، با وجود همه چیزهایی که در راه نیست – بیایید پیش برویم و مرتب سازی شمارش را در پایتون پیاده سازی کنیم:

def countingSort(inputArray):
    
    maxEl = max(inputArray)

    countArrayLength = maxEl+1

    
    countArray = (0) * countArrayLength

    
    
    for el in inputArray: 
        countArray(el) += 1

    
    
    
    
    for i in range(1, countArrayLength):
        countArray(i) += countArray(i-1) 

    
    
    outputArray = (0) * len(inputArray)
    i = len(inputArray) - 1
    while i >= 0:
        currentEl = inputArray(i)
        countArray(currentEl) -= 1
        newPosition = countArray(currentEl)
        outputArray(newPosition) = currentEl
        i -= 1

    return outputArray

inputArray = (2,2,0,6,1,9,9,7)
print("Input array = ", inputArray)

sortedArray = countingSort(inputArray)
print("Counting sort result = ", sortedArray)

با اجرای کد بالا خروجی زیر به دست می آید:

Input array =  (2, 2, 0, 6, 1, 9, 9, 7)
Counting sort result =  (0, 1, 2, 2, 6, 7, 9, 9)

شمارش پیچیدگی مرتب سازی

پیچیدگی زمانی مرتب سازی شمارش است O(n+k)، جایی که n تعداد عناصر موجود در آرایه ورودی، و k ارزش آن است max عنصر در آرایه.

مشکل زمانی رخ می دهد که مقدار بزرگترین عنصر به شدت از تعداد عناصر موجود در آرایه بیشتر شود. به عنوان k نزدیک می شود n²، پیچیدگی زمانی نزدیکتر می شود O(n²)، که پیچیدگی زمانی وحشتناکی برای الگوریتم مرتب سازی است.

اینجا جایی است که مرتب سازی Radix شروع به کار می کند.

الگوریتم مرتب سازی Radix

به جای شمارش عناصر با مقدار کلید متمایزشان – مرتب‌سازی رادیکس ارقام را بر اساس آنها گروه‌بندی می‌کند. ارزش موقعیت و اجرای شمارش مرتب سازی در هر گروه. موقعیت شروع می تواند متفاوت باشد – LSD (کمترین ارقام مهم) یا MSD (مهمترین ارقام) دو نوع متداول هستند و بر این اساس، این تغییرات Radix Sort LSD Radix Sort و MSD Radix Sort نامیده می شوند.

اجازه دهید I = (2, 20, 61, 997, 1, 619) آرایه ورودی باشد که می خواهیم مرتب کنیم:

ما تمرکز می کنیم روی مرتب سازی رادیکس ال اس دی.

الگوریتم مرتب سازی رادیکس

مراحل انجام شده توسط Radix Sort نسبتاً ساده است:

1. حداکثر عنصر را در آرایه ورودی پیدا کنید – max = 997
2. تعداد ارقام موجود در max عنصر – D = 3
3. ارزش مکانی را به کمترین مکان نشان دهید – placeVal = 1
4. برای D زمان انجام:
   1. مرتب سازی شمارش را بر اساس ارزش مکانی فعلی انجام دهید
   2. با ضرب به ارزش مکانی بعدی بروید placeVal توسط 10

روش پیاده سازی مرتب سازی رادیکس در پایتون

و در نهایت، با این کار، بیایید مرتب سازی Radix را در پایتون پیاده سازی کنیم:

def countingSortForRadix(inputArray, placeValue):
    
    
    countArray = (0) * 10
    inputSize = len(inputArray)

    
    
    
    
    for i in range(inputSize): 
        placeElement = (inputArray(i) // placeValue) % 10
        countArray(placeElement) += 1

    for i in range(1, 10):
        countArray(i) += countArray(i-1)

    
    outputArray = (0) * inputSize
    i = inputSize - 1
    while i >= 0:
        currentEl = inputArray(i)
        placeElement = (inputArray(i) // placeValue) % 10
        countArray(placeElement) -= 1
        newPosition = countArray(placeElement)
        outputArray(newPosition) = currentEl
        i -= 1
        
    return outputArray

def radixSort(inputArray):
    
    maxEl = max(inputArray)

    
    D = 1
    while maxEl > 0:
        maxEl /= 10
        D += 1
    
    
    placeVal = 1

    
    outputArray = inputArray
    while D > 0:
        outputArray = countingSortForRadix(outputArray, placeVal)
        placeVal *= 10  
        D -= 1

    return outputArray
    
input = (2,20,61,997,1,619)
print(input)
sorted = radixSort(input)
print(sorted)

با اجرای کد بالا خروجی زیر به دست می آید:

(2, 20, 61, 997, 1, 619)
(1, 2, 20, 61, 619, 997)

پیچیدگی مرتب سازی رادیکس

همانطور که قبلاً بیان کردیم، Radix Sort دارد پیچیدگی زمانی خطی. اگر استفاده کنیم مرتب سازی شمارش به عنوان زیربرنامه اصلی، پیچیدگی مرتب سازی ریشه است O(d(n+k)). دلیلش این است که ما مرتب سازی شمارش را اجرا می کنیم d زمان، و پیچیدگی مرتب سازی شمارش خودش است O(n+k).

نتیجه

مرتب سازی Radix یک الگوریتم مرتب سازی عالی برای استفاده در برخی موارد خاص است. برخی از معیارها حتی نشان داده‌اند که مرتب‌سازی ریشه می‌تواند تا 3 برابر سریع‌تر از سایر الگوریتم‌های مرتب‌سازی عمومی‌تر اجرا شود.

هنگامی که آرایه ورودی کلیدهای کوتاه تری داشته باشد یا محدوده مقادیر عناصر کوچکتر باشد، می درخشد. اما در موارد دیگر، زمانی که دامنه مقادیر عناصر بسیار زیاد است و عناصر دارای ارقام بیش از حد در نمایش خود هستند، پیچیدگی فضای ضعیفی دارد.

این دلیل اصلی این است که مرتب‌سازی ریشه به اندازه برخی دیگر از انواع الگوریتم‌های مرتب‌سازی به طور گسترده مورد استفاده قرار نمی‌گیرد، حتی اگر پیچیدگی زمانی خطی داشته باشد.