از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
مرتب سازی سریع در جاوا اسکریپت به مرتب کردن آیتم های یک لیست در یک ترتیب خاص (عددی یا الفبایی) اشاره دارد. مرتبسازی معمولاً همراه با جستجو استفاده میشود. در طول سالها، الگوریتمهای مرتبسازی زیادی توسعه یافتهاند و یکی از سریعترین آنها تا به امروز، Quicksort است. Quicksort از استراتژی تفرقه بینداز و حکومت کن برای مرتب کردن…
سرفصلهای مطلب
معرفی
مرتب سازی به مرتب کردن آیتم های یک لیست به ترتیب خاص (عددی یا الفبایی) اشاره دارد. مرتبسازی معمولاً همراه با جستجو استفاده میشود.
در طول سالها، الگوریتمهای مرتبسازی زیادی توسعه یافتهاند و یکی از سریعترین الگوریتمهای تا به امروز است مرتب سازی سریع.
Quicksort از استراتژی تقسیم و حکومت کن برای مرتب کردن لیست داده شده از عناصر استفاده می کند. این بدان معنی است که الگوریتم مسئله را به زیرمسئلههای فرعی تقسیم میکند تا زمانی که به اندازه کافی برای حل مستقیم ساده شوند.
از نظر الگوریتمی این می تواند به صورت بازگشتی یا تکراری پیاده سازی شود. با این حال، رویکرد بازگشتی برای این مشکل طبیعی تر است.
درک منطق پشت دسته سریع
بیایید نگاهی به روش عملکرد Quicksort بیندازیم:
- یک عنصر از آرایه را انتخاب کنید. این عنصر را عموماً می نامند محوری. اغلب این عنصر یا اولین یا آخرین عنصر در آرایه است.
- سپس، عناصر آرایه را طوری مرتب کنید که تمام عناصر سمت چپ محور کوچکتر از محور و همه عناصر سمت راست بزرگتر از محور باشند. مرحله نامیده می شود پارتیشن بندی. اگر یک عنصر برابر با محور باشد، مهم نیست روی به کدام سمت می رود
- این را تکرار کنید process به صورت جداگانه برای سمت چپ و راست محور، تا زمانی که آرایه مرتب شود.
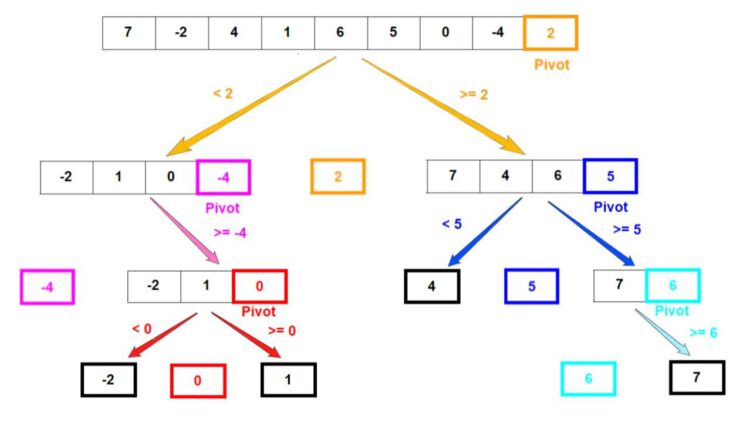
بیایید این مراحل را با قدم زدن در یک مثال بیشتر درک کنیم. آرایه ای از عناصر مرتب نشده را در نظر بگیرید (7, -2, 4, 1, 6, 5, 0, -4, 2). ما آخرین عنصر را به عنوان محور انتخاب می کنیم. تجزیه گام به گام آرایه مانند تصویر زیر است:

عناصری که به عنوان محور در یک مرحله از الگوریتم انتخاب شده اند دارای یک طرح کلی رنگی هستند. پس از پارتیشن بندی، عناصر محوری همیشه در موقعیت صحیح خود در آرایه قرار دارند.
آرایه هایی که دارای یک طرح کلی سیاه پررنگ هستند، پایان آن شاخه بازگشتی خاص را نشان می دهند، زیرا ما به آرایه ای رسیدیم که فقط شامل یک عنصر است.
ما می توانیم مرتب سازی حاصل از این الگوریتم را با عبور از پایین ترین عنصر در هر “ستون” مشاهده کنیم.
پیاده سازی Quicksort در جاوا اسکریپت
همانطور که می بینیم، ستون فقرات این الگوریتم است پارتیشن بندی گام. این مرحله صرف نظر از اینکه از رویکرد بازگشتی یا تکراری استفاده کنیم یکسان است.
با در نظر گرفتن این موضوع، اجازه دهید ابتدا کد را بنویسیم partition() یک آرایه:
function partition(arr, start, end){
// Taking the last element as the pivot
const pivotValue = arr(end);
let pivotIndex = start;
for (let i = start; i < end; i++) {
if (arr(i) < pivotValue) {
// Swapping elements
(arr(i), arr(pivotIndex)) = (arr(pivotIndex), arr(i));
// Moving to next element
pivotIndex++;
}
}
// Putting the pivot value in the middle
(arr(pivotIndex), arr(end)) = (arr(end), arr(pivotIndex))
return pivotIndex;
};
در اینجا، ما آخرین عنصر را به عنوان محور در نظر می گیریم. ما از یک متغیر استفاده می کنیم pivotIndex برای پیگیری موقعیت “وسط” که در آن همه عناصر سمت چپ کمتر هستند و همه عناصر سمت راست بیشتر از pivotValue.
به عنوان آخرین مرحله، ما swap محور، که آخرین عنصر در مورد ما، با pivotIndex. بنابراین، در پایان، عنصر محوری ما در “وسط” قرار می گیرد. با تمام عناصر کمتر از محور در سمت چپ آن، و همه عناصر بزرگتر یا مساوی با محور سمت راست محور.
پیاده سازی بازگشتی
اکنون که ما آن را داریم partition() تابع، ما باید به صورت بازگشتی این مشکل را شکسته و منطق پارتیشن بندی را اعمال کنیم تا مراحل باقی مانده را انجام دهیم:
function quickSortRecursive(arr, start, end) {
// Base case or terminating case
if (start >= end) {
return;
}
// Returns pivotIndex
let index = partition(arr, start, end);
// Recursively apply the same logic to the left and right subarrays
quickSort(arr, start, index - 1);
quickSort(arr, index + 1, end);
}
در این تابع با پارتیشن بندی آرایه شروع می کنیم. پس از آن، هر دو زیرآرایه چپ و راست را پارتیشن بندی می کنیم. ما آن را تکرار می کنیم process تا زمانی که متد آرایه ای را دریافت کند که خالی نباشد یا بیش از یک عنصر داشته باشد.
این به این دلیل است که آرایه های خالی و آرایه هایی با تنها یک عنصر مرتب شده در نظر گرفته می شوند.
بیایید این کد را آزمایش کنیم روی مثال اصلی ما با تماس:
array = (7, -2, 4, 1, 6, 5, 0, -4, 2)
quickSortRecursive(array, 0, array.length - 1)
console.log(array)
این به ما خروجی می دهد:
-4,-2,0,1,2,4,5,6,7
پیاده سازی تکراری
همانطور که قبلا ذکر کردیم، رویکرد بازگشتی به Quicksort بسیار بصری تر است. با این حال، پیاده سازی Quicksort به صورت تکراری یک سوال مصاحبه نسبتاً رایج برای مهندسان نرم افزار است.
مانند بسیاری از تبدیل های بازگشتی به تکراری، اولین چیزی که باید به ذهن متبادر شود استفاده از پشته برای شبیه سازی تماس های بازگشتی است. این کار به این دلیل انجام می شود که بتوانیم برخی از منطق بازگشتی را که با آن آشنا هستیم دوباره استفاده کنیم و از آن در یک تنظیمات تکرار شونده استفاده کنیم.
ما باید به نحوی پیگیری کنیم که چه زیرآرایه های مرتب نشده ای باقی مانده است. یکی از راه های انجام این کار این است که به سادگی “جفت” از عناصر را در یک پشته نگه دارید، که نشان دهنده آن است start و end از یک زیرآرایه مرتب نشده معین.
جاوا اسکریپت ساختار داده پشته ای صریح ندارد، اما آرایه ها از آن پشتیبانی می کنند push() و pop() کارکرد. آنها حمایت نمی کنند peek() با این حال، عملکرد، بنابراین ما باید به صورت دستی بالای پشته را با استفاده از آن بررسی کنیم stack(stack.length - 1).
ما از همان استفاده خواهیم کرد partition مانند روش بازگشتی عمل کرد. بیایید روش نوشتن بخش Quicksort را ببینیم:
function quickSortIterative(arr) {
// Creating an array that we'll use as a stack, using the push() and pop() functions
stack = ();
// Adding the entire initial array as an "unsorted subarray"
stack.push(0);
stack.push(arr.length - 1);
// There isn't an explicit peek() function
// The loop repeats as long as we have unsorted subarrays
while(stack(stack.length - 1) >= 0){
// Extracting the top unsorted subarray
end = stack.pop();
start = stack.pop();
pivotIndex = partition(arr, start, end);
// If there are unsorted elements to the "left" of the pivot,
// we add that subarray to the stack so we can sort it later
if (pivotIndex - 1 > start){
stack.push(start);
stack.push(pivotIndex - 1);
}
// If there are unsorted elements to the "right" of the pivot,
// we add that subarray to the stack so we can sort it later
if (pivotIndex + 1 < end){
stack.push(pivotIndex + 1);
stack.push(end);
}
}
}
بیایید این کد را تست کنیم روی مثال ما نیز با فراخوانی:
ourArray = (7, -2, 4, 1, 6, 5, 0, -4, 2)
quickSortIterative(ourArray)
console.log(ourArray)
ما خروجی مورد انتظار را دریافت می کنیم:
-4,-2,0,1,2,4,5,6,7
تجسم مرتب سازی سریع
وقتی نوبت به مرتبسازی الگوریتمها میرسد، تجسم آنها همیشه خوب است. این فقط به ما کمک می کند آنها را در عمل ببینیم در اینجا مثالی از روش عملکرد الگوریتم Quicksort آورده شده است:

Source: ویکیپدیا
در این مورد، محور نیز به عنوان آخرین عنصر در نظر گرفته می شود. پس از پارتیشن بندی آرایه داده شده، سمت چپ به صورت بازگشتی عبور می کند تا کاملا مرتب شود. سپس الگوریتم به سمت راست می آید و مرتب سازی را انجام می دهد.
کارایی مرتب سازی سریع
اکنون که می دانیم چگونه الگوریتم Quicksort را پیاده سازی کنیم، اجازه دهید پیچیدگی زمان و مکان را مورد بحث قرار دهیم. بدترین پیچیدگی زمانی مرتب سازی سریع است بر2). میانگین پیچیدگی زمانی مورد است O(nlogn). معمولاً با استفاده از نسخه تصادفی Quicksort از بدترین حالت جلوگیری می شود.
نقطه ضعف الگوریتم Quicksort انتخاب محور است. هر بار انتخاب یک محور بد (یکی که بزرگتر از/کمتر از اکثر عناصر است)، در بدترین حالت پیچیدگی زمانی را به ما میدهد. در حالی که انتخاب مکرر محوری که دارای تعداد تقریباً مساوی از عناصر است که کمتر از / بزرگتر از محور هستند، به ما پیچیدگی زمانی می دهد. O(nlogn).
Quicksort یکی از آن الگوریتمهایی است که در آن زمان اجرا میانگین مورد مهم است. از نظر تجربی، مشاهده شد که Quicksort تمایل دارد یک O(nlogn) زمان اجرا صرف نظر از استراتژی انتخاب محوری.
همچنین، در مورد پیچیدگی فضا، Quicksort هیچ فضای اضافی (به استثنای فضای رزرو شده برای تماسهای بازگشتی) نمیگیرد. این نوع الگوریتم ها از نظر فنی به نام نامیده می شوند درجا الگوریتم ها چون در حال انجام عملیات هستیم نیازی به فضای اضافی نداریم روی همان آرایه
نتیجه
در این مقاله، تئوری Quicksort را بررسی کردیم و سپس آن را به صورت بازگشتی و تکراری با استفاده از جاوا اسکریپت پیاده سازی کردیم.
منتشر شده در 1403-01-19 05:08:03



