از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
مرتب سازی سطلی در پایتون
سرفصلهای مطلب
معرفی
در این آموزش، به تئوری و پیاده سازی Bucket Sort در پایتون می پردازیم.
مرتبسازی سطلی یک الگوریتم از نوع مقایسه است که عناصر فهرستی را که میخواهیم در آن مرتبسازی کنیم، اختصاص میدهد. سطل، یا سطل ها. سپس محتویات این سطل ها، معمولاً با الگوریتم دیگری مرتب می شوند. پس از مرتب سازی، محتویات سطل ها ضمیمه می شوند و یک مجموعه مرتب شده را تشکیل می دهند.
Bucket Sort را می توان به عنوان یک در نظر گرفت پراکنده-نظم-جمع کردن رویکرد به مرتبسازی یک لیست، به دلیل این واقعیت است که عناصر اول هستند پراکنده شده است در سطل، سفارش داده شده درون آنها و در نهایت جمع آوری کرد به یک لیست مرتب شده جدید
ما مرتبسازی سطلی را در پایتون پیادهسازی میکنیم و پیچیدگی زمانی آن را تحلیل میکنیم.
مرتب سازی سطلی چگونه کار می کند؟
قبل از پرداختن به اجرای دقیق آن، اجازه دهید مراحل الگوریتم را طی کنیم:
- لیستی از سطل های خالی تنظیم کنید. یک سطل برای هر عنصر در آرایه مقداردهی اولیه می شود.
- در لیست سطلی تکرار کنید و عناصر را از آرایه درج کنید. جایی که هر عنصر درج می شود بستگی دارد روی لیست ورودی و بزرگترین عنصر آن. ما می توانیم به پایان برسیم
0..nعناصر در هر سطل این به تفصیل خواهد آمد روی در ارائه بصری الگوریتم - هر سطل غیر خالی را مرتب کنید. شما می توانید این کار را با هر الگوریتم مرتب سازی از آنجایی که ما با یک مجموعه داده کوچک کار می کنیم، هر سطل دارای عناصر زیادی نخواهد بود مرتب سازی درج اینجا برای ما معجزه می کند.
- به ترتیب از سطل ها دیدن کنید. هنگامی که محتویات هر سطل مرتب شد، هنگامی که به هم پیوستند، فهرستی به دست میآید که در آن عناصر بر اساس مرتب شدهاند. روی معیارهای شما
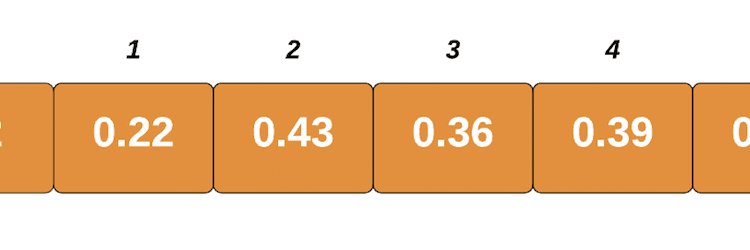
بیایید نگاهی به ارائه بصری روش عملکرد الگوریتم بیندازیم. به عنوان مثال، فرض کنید این لیست ورودی است:

بزرگترین عنصر است 1.2، و طول لیست است 6. با استفاده از این دو، بهینه را کشف خواهیم کرد size از هر سطل این عدد را با تقسیم بزرگترین عنصر با طول لیست بدست می آوریم. در مورد ما، این است 1.2/6 که هست 0.2.
با تقسیم مقدار عنصر با این size، برای سطل مربوط به هر عنصر یک شاخص دریافت می کنیم.
اکنون، سطل های خالی ایجاد می کنیم. ما به اندازه عناصر موجود در لیست خود سطل خواهیم داشت:

ما عناصر را در سطل مربوطه خود وارد می کنیم. با در نظر گرفتن اولین عنصر – 1.2/0.2 = 6، شاخص سطل مربوطه آن است 6. اگر این نتیجه بزرگتر یا مساوی طول لیست باشد، فقط کم می کنیم 1 و به خوبی در لیست قرار می گیرد. این فقط با بیشترین تعداد اتفاق میافتد، زیرا ما عدد را دریافت کردیم size با تقسیم بزرگترین عنصر بر طول.
ما این عنصر را در سطلی با شاخص قرار می دهیم 5:

به همین ترتیب، عنصر بعدی به ایندکس خواهد شد 0.22/0.2 = 1.1. از آنجایی که این یک عدد اعشاری است، آن را طبقه بندی می کنیم. این گرد شده است 1، و عنصر ما در سطل دوم قرار می گیرد:

این process تکرار می شود تا زمانی که آخرین عنصر را در سطل مربوطه آن قرار دهیم. اکنون سطلهای ما چیزی شبیه به موارد زیر است:

اکنون، محتویات هر سطل غیر خالی را مرتب می کنیم. ما از Insertion Sort استفاده خواهیم کرد زیرا با لیست های کوچکی مانند این شکست ناپذیر است. پس از Insertion Sort، سطل ها به شکل زیر هستند:

اکنون، فقط باید از سطلهای خالی عبور کرد و عناصر را در یک لیست به هم متصل کرد. آنها مرتب شده اند و آماده رفتن هستند:

پیاده سازی مرتب سازی سطلی در پایتون
با وجود این موضوع، بیایید پیش برویم و الگوریتم را در پایتون پیاده سازی کنیم. بیایید با bucket_sort() خود عملکرد:
def bucket_sort(input_list):
max_value = max(input_list)
size = max_value/len(input_list)
buckets_list= ()
for x in range(len(input_list)):
buckets_list.append(())
for i in range(len(input_list)):
j = int (input_list(i) / size)
if j != len (input_list):
buckets_list(j).append(input_list(i))
else:
buckets_list(len(input_list) - 1).append(input_list(i))
for z in range(len(input_list)):
insertion_sort(buckets_list(z))
final_output = ()
for x in range(len (input_list)):
final_output = final_output + buckets_list(x)
return final_output
پیاده سازی نسبتاً ساده است. ما محاسبه کرده ایم size پارامتر. سپس، فهرستی از سطلهای خالی و عناصر را بر اساس درج کردیم روی ارزش آنها و size از هر سطل
پس از درج، ما تماس می گیریم insertion_sort() روی هر یک از سطل ها:
def insertion_sort(bucket):
for i in range (1, len (bucket)):
var = bucket(i)
j = i - 1
while (j >= 0 and var < bucket(j)):
bucket(j + 1) = bucket(j)
j = j - 1
bucket(j + 1) = var
و با وجود آن، بیایید یک لیست را پر کنیم و یک مرتب سازی سطلی انجام دهیم روی آی تی:
def main():
input_list = (1.20, 0.22, 0.43, 0.36,0.39,0.27)
print('ORIGINAL LIST:')
print(input_list)
sorted_list = bucket_sort(input_list)
print('SORTED LIST:')
print(sorted_list)
اجرای این کد باز خواهد گشت:
Original list: (1.2, 0.22, 0.43, 0.36, 0.39, 0.27)
Sorted list: (0.22, 0.27, 0.36, 0.39, 0.43, 1.2)
پیچیدگی زمان مرتبسازی سطلی
پیچیدگی در بدترین حالت
اگر مجموعه ای که با آن کار می کنیم محدوده کوتاهی داشته باشد (مانند نمونه ای که در مثال خود داشتیم) – معمولاً عناصر زیادی در یک سطل وجود دارند که در آن تعداد زیادی سطل خالی هستند.
اگر همه عناصر در یک سطل قرار گیرند، پیچیدگی به طور انحصاری بستگی دارد روی الگوریتمی که برای مرتب کردن محتویات خود سطل استفاده می کنیم.
از آنجایی که ما از Insertion Sort استفاده می کنیم – وقتی لیست به ترتیب معکوس باشد، پیچیدگی آن در بدترین حالت می درخشد. بنابراین، بدترین پیچیدگی برای مرتب سازی سطلی نیز وجود دارد بر2).
پیچیدگی بهترین حالت
بهترین حالت این است که همه عناصر از قبل مرتب شده باشند. علاوه بر این، عناصر به طور یکنواخت توزیع شده اند. این بدان معناست که هر سطل دارای همان تعداد عناصر خواهد بود.
همانطور که گفته شد، ایجاد سطل ها طول می کشد بر) و مرتب سازی درج خواهد شد خوب)، به ما یک O(n+k) پیچیدگی
میانگین پیچیدگی پرونده
میانگین مورد در اکثریت قریب به اتفاق مجموعه های واقعی رخ می دهد. وقتی مجموعه ای که می خواهیم مرتب کنیم باشد تصادفی. در آن صورت، Bucket Sort می گیرد بر) به پایان رساندن، ساختن آن بسیار کارآمد.
نتیجه
برای جمع بندی همه چیز، ما با مقدمه ای در مورد چیدمان سطلی شروع کردیم و رفتیم روی قبل از اینکه به پیاده سازی آن در پایتون بپردازیم، درباره آنچه باید بدانیم بحث کنیم. پس از پیاده سازی، ما یک تحلیل پیچیدگی سریع انجام داده ایم.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-17 02:06:03



