نمادگذاری Big O و تجزیه و تحلیل الگوریتم با مثال های پایتون

معرفی

معمولا چندین راه برای حل مشکل با استفاده از یک برنامه کامپیوتری وجود دارد. برای مثال، چندین روش برای مرتب‌سازی آیتم‌ها در یک آرایه وجود دارد – می‌توانید از مرتب‌سازی ادغام، مرتب‌سازی حبابی، مرتب‌سازی درج و غیره استفاده کنید. روی. همه این الگوریتم ها مزایا و معایب خاص خود را دارند و وظیفه توسعه دهنده این است که آنها را وزن کند تا بتواند بهترین الگوریتم را برای استفاده در هر موردی انتخاب کند. به عبارت دیگر، سوال اصلی این است از کدام الگوریتم برای حل یک مسئله خاص استفاده کنید زمانی که چندین راه حل برای مشکل وجود دارد.

تحلیل الگوریتم به تجزیه و تحلیل پیچیدگی الگوریتم های مختلف و یافتن کارآمدترین الگوریتم برای حل مسئله در دست اشاره دارد. نماد Big-O هست یک اندازه گیری آماری مورد استفاده برای توصیف پیچیدگی الگوریتم.

در این راهنما، ابتدا مروری کوتاه بر تحلیل الگوریتم خواهیم داشت و سپس نگاهی عمیق‌تر به نماد Big-O خواهیم داشت. خواهیم دید که چگونه می توان از نماد Big-O برای یافتن پیچیدگی الگوریتم با کمک توابع مختلف پایتون استفاده کرد.

چرا تحلیل الگوریتم مهم است؟

برای درک اینکه چرا تحلیل الگوریتم مهم است، از یک مثال ساده استفاده می کنیم. فرض کنید مدیری به دو نفر از کارمندان خود وظیفه می دهد تا الگوریتمی در پایتون طراحی کنند که محاسبه کند. فاکتوریل یک عدد وارد شده توسط کاربر الگوریتم توسعه یافته توسط اولین کارمند به صورت زیر است:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

توجه داشته باشید که الگوریتم به سادگی یک عدد صحیح را به عنوان آرگومان می گیرد. درون fact() تابع متغیری به نام product به مقدار دهی اولیه می شود 1. یک حلقه از 1 به n و در طول هر تکرار، مقدار در product در عددی که توسط حلقه تکرار می شود ضرب می شود و نتیجه در آن ذخیره می شود product دوباره متغیر پس از اجرای حلقه، product متغیر حاوی فاکتوریل خواهد بود.

به طور مشابه، کارمند دوم نیز الگوریتمی را توسعه داد که فاکتوریل یک عدد را محاسبه می کند. کارمند دوم از یک تابع بازگشتی برای محاسبه فاکتوریل عدد استفاده کرد n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

مدیر باید تصمیم بگیرد که از کدام الگوریتم استفاده کند. برای انجام این کار، آنها تصمیم گرفته اند انتخاب کنند که کدام الگوریتم سریعتر اجرا شود. یکی از راه‌های انجام این کار، یافتن زمان لازم برای اجرای کد است روی همان ورودی

در Jupyter نوت بوک، شما می توانید استفاده کنید %timeit تحت اللفظی به دنبال فراخوانی تابع برای یافتن زمان صرف شده توسط تابع برای اجرا:

%timeit fact(50)

این به ما می دهد:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

خروجی می گوید که الگوریتم طول می کشد 9 میکروثانیه (بعلاوه/منهای 45 نانوثانیه) در هر حلقه.

به طور مشابه، می‌توانیم محاسبه کنیم که روش دوم چقدر زمان می‌برد تا اجرا شود:

%timeit fact2(50)

این منجر به:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

الگوریتم دوم که شامل بازگشت است 15 میکروثانیه (بعلاوه/منهای 427 نانوثانیه).

زمان اجرا نشان می دهد که الگوریتم اول در مقایسه با الگوریتم دوم شامل بازگشت سریعتر است. هنگام برخورد با ورودی های بزرگ، تفاوت عملکرد می تواند قابل توجه تر شود.

با این حال، زمان اجرا است معیار خوبی نیست برای اندازه گیری پیچیدگی یک الگوریتم، زیرا به سخت افزار بستگی دارد. یک معیار تحلیل پیچیدگی عینی تری برای یک الگوریتم مورد نیاز است.

اینجاست که نماد O بزرگ وارد بازی می شود!

تجزیه و تحلیل الگوریتم با علامت گذاری Big-O

این نماد Big-O ارتباط بین ورودی به الگوریتم و مراحل لازم برای اجرای الگوریتم را نشان می دهد.

با یک “O” بزرگ و به دنبال پرانتز باز و بسته نشان داده می شود. در داخل پرانتز، رابطه بین ورودی و مراحل انجام شده توسط الگوریتم با استفاده از “n” ارائه شده است.

نکته کلیدی این است – Big-O به a علاقه ای ندارد خاص نمونه ای که در آن الگوریتمی را اجرا می کنید، مانند fact(50)، بلکه در آن چقدر خوب است ترازو با توجه به ورودی فزاینده این معیار بسیار بهتری برای ارزیابی نسبت به زمان مشخص برای یک نمونه واقعی است!

به عنوان مثال، اگر وجود دارد رابطه خطی بین ورودی و گامی که الگوریتم برای تکمیل اجرای آن برداشته است، نماد Big-O مورد استفاده قرار خواهد گرفت. بر). به طور مشابه، نماد Big-O برای توابع درجه دوم است O (n²).

برای ایجاد شهود:

• بر): در n=1، 1 مرحله برداشته شده است. در n=10، 10 مرحله انجام می شود.
• O (n²): در n=1، 1 مرحله برداشته شده است. در n=10، 100 قدم برداشته می شود.

در n=1، این دو همان کار را انجام می دهند! این یکی دیگر از دلایل رعایت رابطه بین ورودی و تعداد مراحل به است process این ورودی بهتر از ارزیابی عملکردها با مقداری ورودی مشخص است.

در زیر برخی از رایج ترین توابع Big-O آمده است:

نام	بیگ O
ثابت	O(c)
خطی	بر)
درجه دوم	O (n²)
مکعبی	O (n³)
نمایی	O(2)
لگاریتمی	O(log(n))
ورود به سیستم خطی	O(nlog(n))

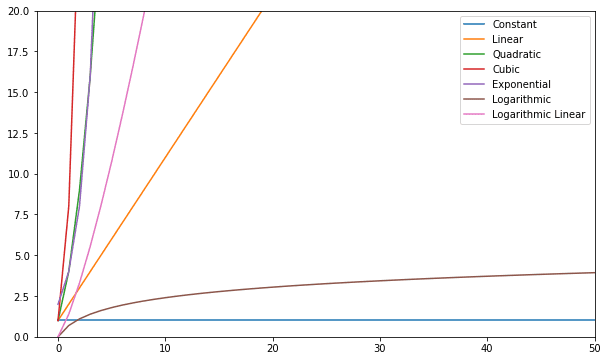
می توانید این توابع را تجسم کرده و آنها را با هم مقایسه کنید:

به طور کلی – هر چیزی بدتر از خطی یک پیچیدگی بد در نظر گرفته می شود (یعنی ناکارآمد) و در صورت امکان باید از آن اجتناب کرد. پیچیدگی خطی مشکلی ندارد و معمولاً یک شر ضروری است. لگاریتمی خوب است. ثابت شگفت انگیز است!

برای دریافت ایده ای از روش محاسبه Big-O، اجازه دهید نگاهی به چند مثال از پیچیدگی ثابت، خطی و درجه دوم بیندازیم.

پیچیدگی ثابت – O(C)

پیچیدگی یک الگوریتم ثابت است اگر مراحل لازم برای تکمیل اجرای یک الگوریتم بدون توجه به تعداد ورودی‌ها ثابت بماند. پیچیدگی ثابت با نشان داده می شود O(c) جایی که ج می تواند هر عدد ثابتی باشد.

بیایید یک الگوریتم ساده در پایتون بنویسیم که مربع اولین آیتم لیست را پیدا کند و سپس آن را چاپ کند. روی صفحه نمایش:

def constant_algo(items):
    result = items(0) * items(0)
    print(result)

constant_algo((4, 5, 6, 8))

در اسکریپت بالا، صرف نظر از اندازه ورودی، یا تعداد موارد موجود در لیست ورودی items، الگوریتم فقط 2 مرحله را انجام می دهد:

1. پیدا کردن مربع عنصر اول
2. چاپ نتیجه روی صفحه نمایش

از این رو، پیچیدگی ثابت می ماند.

اگر یک نمودار خطی با اندازه های مختلف ترسیم کنید items ورودی روی محور X و تعداد مراحل روی در محور Y، یک خط مستقیم خواهید داشت. بیایید یک اسکریپت کوتاه بسازیم تا به ما در تجسم این موضوع کمک کند. بدون توجه به تعداد ورودی ها، تعداد مراحل اجرا شده ثابت می ماند:

steps = ()
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

پیچیدگی خطی – بر)

پیچیدگی یک الگوریتم خطی است اگر مراحل لازم برای تکمیل اجرای یک الگوریتم به صورت خطی با تعداد ورودی ها افزایش یا کاهش یابد. پیچیدگی خطی با نشان داده می شود بر).

در این مثال، اجازه دهید یک برنامه ساده بنویسیم که تمام موارد موجود در لیست را به نمایش در می آورد console:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo((4, 5, 6, 8))

پیچیدگی از linear_algo() تابع در مثال بالا خطی است زیرا تعداد تکرارهای حلقه for خواهد بود برابر با اندازه ورودی items آرایه. به عنوان مثال، اگر 4 مورد در آن وجود داشته باشد items در لیست، حلقه for 4 بار اجرا می شود.

بیایید به سرعت یک نمودار برای الگوریتم پیچیدگی خطی با تعداد ورودی ها ایجاد کنیم روی محور x و تعداد مراحل روی محور y:

steps = ()
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

این منجر به:

نکته مهمی که باید به آن توجه داشت این است که با ورودی های بزرگ، ثابت ها تمایل به از دست دادن ارزش دارند. به همین دلیل است که ما معمولاً ثابت ها را از نماد Big-O حذف می کنیم و عبارتی مانند O(2n) معمولاً به O(n) کوتاه می شود. هر دو O(2n) و O(n) خطی هستند – رابطه خطی مهم است، نه مقدار مشخص. به عنوان مثال، اجازه دهید تغییر دهید linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo((4, 5, 6, 8))

دو حلقه for وجود دارد که روی ورودی تکرار می شوند items فهرست بنابراین پیچیدگی الگوریتم می شود O(2n)اما در مورد موارد نامتناهی در لیست ورودی، دو برابر بینهایت همچنان برابر با بی نهایت است. می توانیم ثابت را نادیده بگیریم 2 (از آنجایی که در نهایت ناچیز است) و پیچیدگی الگوریتم باقی می ماند بر).

بیایید این الگوریتم جدید را با ترسیم ورودی ها تجسم کنیم روی محور X و تعداد مراحل روی محور Y:

steps = ()
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

در اسکریپت بالا، به وضوح می توانید آن را ببینید y=2nبا این حال، خروجی خطی است و به شکل زیر است:

پیچیدگی درجه دوم – O (n²)

پیچیدگی یک الگوریتم زمانی به درجه دوم گفته می شود که مراحل مورد نیاز برای اجرای یک الگوریتم تابع درجه دوم تعداد آیتم های ورودی باشد. پیچیدگی درجه دوم به صورت نشان داده می شود O (n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo((4, 5, 6, 8))

ما یک حلقه بیرونی داریم که در تمام موارد موجود در لیست ورودی تکرار می شود و سپس یک حلقه داخلی تو در تو، که دوباره از طریق تمام موارد در لیست ورودی تکرار می شود. تعداد کل مراحل انجام شده n*n است که n تعداد موارد موجود در آرایه ورودی است.

نمودار زیر تعداد ورودی ها را در برابر مراحل یک الگوریتم با پیچیدگی درجه دوم ترسیم می کند:

پیچیدگی لگاریتمی – O(logn)

برخی از الگوریتم ها به پیچیدگی لگاریتمی دست می یابند، مانند جستجوی باینری. جستجوی دودویی یک عنصر در یک آرایه را با علامت زدن نشان می دهد وسط از یک آرایه، و هرس نیمه ای که عنصر در آن نیست. این کار را دوباره برای نیمه باقی مانده انجام می دهد و همان مراحل را ادامه می دهد تا عنصر پیدا شود. در هر مرحله، آن نیمه ها تعداد عناصر آرایه

این امر مستلزم مرتب‌سازی آرایه است و فرضیاتی در مورد داده‌ها (مانند مرتب‌سازی آن‌ها) وجود دارد.

زمانی که بتوانید در مورد داده های دریافتی مفروضاتی بسازید، می توانید اقداماتی را انجام دهید که پیچیدگی یک الگوریتم را کاهش می دهد. پیچیدگی لگاریتمی مطلوب است، زیرا عملکرد خوبی را حتی با ورودی های با مقیاس بالا به دست می آورد.

پیدا کردن پیچیدگی توابع پیچیده؟

در مثال های قبلی، توابع نسبتا ساده ای داشتیم روی ورودی با این حال، چگونه Big-O توابعی را که (چندین) توابع دیگر را فراخوانی می کنند محاسبه کنیم روی ورودی؟

بیا یک نگاهی بیندازیم:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo((4, 5, 6, 8))

در اسکریپت بالا چندین کار در حال انجام است، ابتدا یک رشته 5 بار چاپ می شود روی را console با استفاده از print بیانیه. بعد، ما print لیست ورودی دو بار روی صفحه و در نهایت یک رشته دیگر سه بار چاپ می شود روی را console. برای یافتن پیچیدگی چنین الگوریتمی، باید کد الگوریتم را به بخش‌هایی تقسیم کنیم و سعی کنیم پیچیدگی تک تک قطعات را پیدا کنیم. پیچیدگی هر قطعه را مشخص کنید.

در بخش اول داریم:

for i in range(5):
    print("Python is awesome")

پیچیدگی این قسمت است O (5) از آنجایی که پنج مرحله ثابت بدون توجه به ورودی در این قطعه کد انجام می شود.

بعد، داریم:

for item in items:
    print(item)

ما می دانیم که پیچیدگی قطعه کد بالا است بر). به طور مشابه، پیچیدگی قطعه کد زیر نیز هست بر):

for item in items:
    print(item)

در نهایت، در قطعه کد زیر، یک رشته سه بار چاپ می شود، بنابراین پیچیدگی آن است O (3):

print("Big O")
print("Big O")
print("Big O")

برای یافتن پیچیدگی کلی، ما به سادگی باید این پیچیدگی های فردی را اضافه کنیم:

O(5) + O(n) + O(n) + O(3)

با ساده سازی موارد فوق به دست می آوریم:

O(8) + O(2n) = O(8+2n)

قبلاً گفتیم که وقتی ورودی (که در این مورد دارای طول n است) بسیار بزرگ می شود، ثابت ها ناچیز می شوند، یعنی دو یا نیمی از بی نهایت همچنان بی نهایت باقی می ماند. بنابراین، می توانیم ثابت ها را نادیده بگیریم. پیچیدگی نهایی الگوریتم خواهد بود بر)!

بدترین در مقابل بهترین پیچیدگی پرونده

معمولاً وقتی کسی از شما در مورد پیچیدگی یک الگوریتم می پرسد – به بدترین پیچیدگی (Big-O) علاقه مند است. گاهی اوقات، آنها ممکن است به پیچیدگی بهترین حالت نیز علاقه مند شوند (Big-Omega).

برای درک رابطه بین اینها، اجازه دهید به کد دیگری نگاهی بیندازیم:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = (2, 4, 6, 8, 10)

print(search_algo(2, nums))

در اسکریپت بالا تابعی داریم که یک عدد و لیستی از اعداد را به عنوان ورودی می گیرد. اگر عدد ارسال شده در لیست اعداد یافت شود، مقدار true را برمی گرداند، در غیر این صورت، برمی گردد None. اگر 2 را در لیست جستجو کنید، در مقایسه اول پیدا می شود. این پیچیدگی در بهترین حالت الگوریتم است زیرا مورد جستجو شده در اولین فهرست جستجو یافت می شود. بهترین پیچیدگی مورد، در این مورد است O (1). از طرف دیگر، اگر 10 را جستجو کنید، در آخرین فهرست جستجو پیدا می شود. از این رو، الگوریتم باید تمام موارد موجود در لیست را جستجو کند بدترین پیچیدگی تبدیل می شود بر).

علاوه بر پیچیدگی بهترین و بدترین حالت، می توانید محاسبه کنید پیچیدگی متوسط (بیگ تتا) یک الگوریتم، که به شما می گوید “با توجه به یک ورودی تصادفی، پیچیدگی زمانی مورد انتظار الگوریتم چقدر است”؟

پیچیدگی فضا

علاوه بر پیچیدگی زمانی، که در آن تعداد مراحل لازم برای تکمیل اجرای یک الگوریتم را می شمارید، می توانید پیچیدگی فضا که به میزان فضایی که باید در حین اجرای یک برنامه در حافظه اختصاص دهید اشاره دارد.

به مثال زیر دقت کنید:

def return_squares(n):
    square_list = ()
    for num in n:
        square_list.append(num * num)

    return square_list

nums = (2, 4, 6, 8, 10)
print(return_squares(nums))

این return_squares() تابع لیستی از اعداد صحیح را می پذیرد و لیستی با مربع های مربوطه را برمی گرداند. الگوریتم باید به همان تعداد آیتم هایی که در لیست ورودی است حافظه اختصاص دهد. بنابراین، پیچیدگی فضایی الگوریتم می شود بر).

نتیجه

نماد Big-O معیار استانداردی است که برای اندازه گیری پیچیدگی یک الگوریتم استفاده می شود. در این راهنما، ما نشان‌گذاری Big-O چیست و چگونه می‌توان از آن برای اندازه‌گیری پیچیدگی انواع الگوریتم‌ها استفاده کرد. ما همچنین انواع مختلف توابع Big-O را با کمک مثال های مختلف پایتون مطالعه کردیم. در نهایت بدترین و بهترین پیچیدگی موردی را به همراه پیچیدگی فضا به اختصار بررسی کردیم.