از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
پرش جستجو در پایتون
سرفصلهای مطلب
معرفی
یافتن داده های مناسبی که نیاز داریم یک مشکل قدیمی قبل از رایانه است. به عنوان توسعهدهندگان، ما الگوریتمهای جستجوی زیادی را برای بازیابی کارآمد دادهها ایجاد میکنیم.
الگوریتم های جستجو را می توان به دو دسته کلی تقسیم کرد: متوالی و فاصله جستجوها جستجوهای متوالی هر عنصر را در یک ساختار داده بررسی می کنند. جستجوهای فاصله ای نقاط مختلف داده را بررسی می کنند (به نام فواصل)، زمان لازم برای یافتن یک مورد را با توجه به مجموعه داده مرتب شده کاهش می دهند.
در این مقاله پوشش خواهید داد پرش جستجو در پایتون – ترکیبی ترکیبی از جستجوی متوالی و جستجوی فاصله ای روی آرایه های مرتب شده
جستجوی پرش
با جستجوی پرش، آرایه مرتب شده از داده ها به زیر مجموعه هایی از عناصر به نام بلوک تقسیم می شود. با مقایسه کلید جستجو (مقدار ورودی) را پیدا می کنیم کاندید جستجو در هر بلوک همانطور که آرایه مرتب شده است، کاندید جستجو بالاترین مقدار یک بلوک است.
هنگام مقایسه کلید جستجو با یک نامزد جستجو، الگوریتم می تواند 1 از 3 کار را انجام دهد:
- اگر نامزد جستجو کوچکتر از کلید جستجو باشد، بلوک بعدی را بررسی می کنیم
- اگر نامزد جستجو بزرگتر از کلید جستجو باشد، یک جستجوی خطی انجام می دهیم روی بلوک فعلی
- اگر نامزد جستجو با کلید جستجو یکسان است، نامزد را برگردانید
اندازه بلوک به عنوان مربع انتخاب می شود root از طول آرایه بنابراین، آرایه های با طول n اندازه بلوک دارند √n، به این صورت روی میانگین بهترین عملکرد را برای اکثر آرایه ها ارائه می دهد.
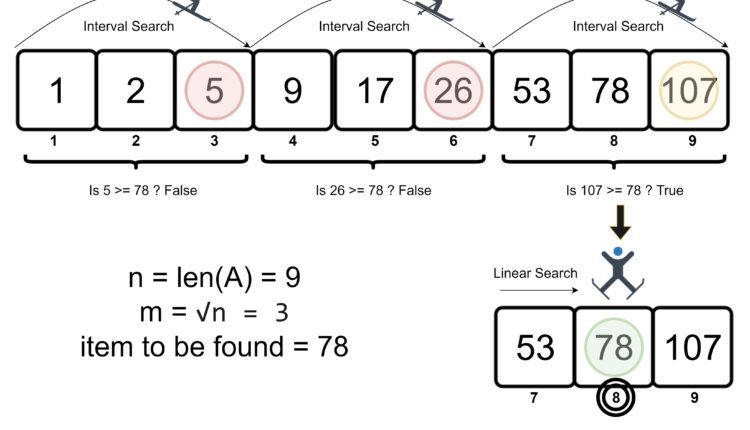
توضیح روش کارکرد آن ممکن است مفید باشد. در اینجا آمده است که چگونه Jump Search مقدار 78 را در آرایه ای از 9 عنصر پیدا می کند:

مثال بالا عنصر را در 5 مرحله پیدا می کند، زیرا دو بررسی در بخش جستجوی خطی وجود دارد.
اکنون که درک سطح بالایی از روش عملکرد آن داریم، بیایید به اجرای شبه کد الگوریتم نگاه کنیم.
پرش مراحل جستجو
ورودی ها:
- آرایه/فهرست
Aاز اندازهn - کلید جستجو
item
خروجی:
- فهرست کلید جستجوی منطبق یا
-1اگرitemیافت نشد
مراحل
- مرحله 1: طول مرتب شده را پیدا کنید فهرست منبع –
n = len(A) - گام 2: اندازه بلوک مناسب را تعیین کنید –
m = √n - مرحله 3: تکرار از شاخص شروع می شود
itemدرi = 0با یک قدم ازmو تا زمانی که پنجره به انتهای لیست برسد ادامه می یابد. - مرحله 4: مقایسه کنید
A(i+m)(i+mآخرین شاخص یک بلوک است) وitem- آ) اگر
A(i+m) == item، برگشتi+m; کد خارج می شود - ب) اگر
A(i+m) > item، به جستجوی خطی در داخل بلوک معروف به عنوان ادامه دهید لیست مشتق شدهB = A(i: i+m)- هر عنصر لیست را با کلید جستجو تکرار و مقایسه کنید و مطابقت را برگردانید
iدر صورت یافتن؛ کد خارج می شود
- هر عنصر لیست را با کلید جستجو تکرار و مقایسه کنید و مطابقت را برگردانید
- ج) اگر
A(i+m) < item، با تکرار بعدی به مرحله 4 بروید: arrows_clockwise:
- آ) اگر
- مرحله 5: عناصر لیست را که در بلوک نمی گنجند تکرار کنید و شاخص تطبیق را برگردانید
i. اگر مطابقت پیدا نشد، برگردید-1; کد خارج می شود
همانطور که اکنون متوجه شدیم که چگونه کار می کند، اجازه دهید این الگوریتم را در پایتون پیاده سازی کنیم!
پیاده سازی
با دانستن اینکه Jump Search چگونه کار می کند، بیایید جلوتر برویم و آن را در Python پیاده سازی کنیم:
'''
Jump Search function
Arguments:
A - The source list
item - Element for which the index needs to be found
'''
import math
def jump_search(A, item):
print("Entering Jump Search")
n = len(A)
m = int(math.sqrt(n))
i = 0
while i != len(A)-1 and A(i) < item:
print("Processing Block - {}".format(A(i: i+m)))
if A(i+m-1) == item:
return i+m-1
elif A(i+m-1) > item:
B = A(i: i+m-1)
return linear_search(B, item, i)
i += m
B = A(i:i+m)
print("Processing Block - {}".format(B))
return linear_search(B, item, i)
این jump_search() تابع دو آرگومان می گیرد – لیست مرتب شده در حال ارزیابی به عنوان آرگومان اول و عنصری که باید در آرگومان دوم یافت شود. این math.sqrt() تابع برای یافتن اندازه بلوک استفاده می شود. تکرار توسط a تسهیل می شود while شرط و افزایش با افزایش امکان پذیر می شود i += m.
شما متوجه شده اید که Step 4b و Step 5 داشتن یک linear_search() تابع فراخوانی شد این linear_search() عملکرد در یکی از سناریوهای زیر فعال می شود.
-
Step 4b– وقتی وجود دارد تغییر در مقایسه. اگر آخرین عنصر یک بلوک/پنجره بزرگتر ازitem،linear_search()تحریک می شود. -
Step 5– عناصر باقی مانده از فهرست منبعAکه در یک بلوک قرار نمی گیرند به عنوان یک لیست مشتق شده به آن ارسال می شوندlinear_search()تابع.
این linear_search() تابع را می توان به صورت زیر نوشت:
'''
Linear Search function
Arguments:
B - The derived list
item - Element for which the index needs to be found
loc - The Index where the remaining block begins
'''
def linear_search(B, item, loc):
print("\t Entering Linear Search")
i = 0
while i != len(B):
if B(i) == item:
return loc+i
i += 1
return -1
در مرحله 5، عناصر باقی مانده از لیست اصلی به قسمت ارسال می شوند linear_search() به عنوان یک لیست مشتق شده عمل کنید. مقایسه با هر عنصر از لیست مشتق شده انجام می شود B.
نمایه مطابق فهرست مشتق شده به نمایه بلوک منبع اضافه می شود تا موقعیت شاخص دقیق عنصر در لیست منبع ارائه شود. اگر هیچ مسابقه ای یافت نشد، ما برمی گردیم -1 برای نشان دادن آن item پیدا نشد
قطعه کامل را می توان یافت روی GitHub.
معیار – جستجوی پرش در مقابل جستجوی خطی
زمان اجرا برای جستجوی پرش را می توان با جستجوی خطی محک زد. تجسم زیر روش عملکرد الگوریتم ها را هنگام جستجوی یک عنصر نزدیک به انتهای یک آرایه مرتب شده نشان می دهد. هرچه نوار کوتاهتر باشد، بهتر است:

با افزایش تعداد عناصر در لیست، جستجوی پرش سریعتر از الگوریتم جستجوی خطی است.
تجزیه و تحلیل Big-O
بیایید یک تحلیل کلی تر از روش عملکرد Jump Search انجام دهیم. ما یک بار دیگر بدترین سناریو را در نظر خواهیم گرفت که در آن عنصری که باید پیدا شود در انتهای لیست قرار دارد.
برای لیستی از n عناصر و اندازه بلوک از m، جستجوی پرش به طور ایده آل انجام می شود n/m می پرد. با در نظر گرفتن اندازه بلوک √n، زمان اجرا نیز خواهد بود O(√n).
این امر Jump Search را بین جستجوی خطی (بدترین) با پیچیدگی زمان اجرا قرار می دهد O(n) و جستجوی باینری (بهترین) با پیچیدگی زمان اجرا O(log n). از این رو، جستجوی پرش را می توان در مکان هایی استفاده کرد که جستجوی باینری امکان پذیر نیست و جستجوی خطی بسیار پرهزینه است.
نتیجه
در این مقاله به اصول اولیه الگوریتم جستجوی پرش پرداخته ایم. سپس روش عملکرد Jump Search با شبه کد را قبل از اجرای آن در پایتون بررسی کردیم. پس از آن، روش عملکرد Jump Search و همچنین محدودیتهای سرعت نظری آن را تحلیل کردیم.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-13 19:52:04



