سرور مجازی NVMe

چگونه معادله بلک اسکولز کار می کند – با مثال های کد پایتون توضیح داده شده است

Python

توسط تیم تولید محتوا در خرداد ۲۸, ۱۴۰۳

چگونه معادله بلک اسکولز کار می کند - با مثال های کد پایتون توضیح داده شده است

سرفصلهای مطلب

زمان لازم برای مطالعه: 6 دقیقه

معادله بلک اسکولز احتمالاً یکی از تاثیرگذارترین معادلاتی است که هیچکس درباره آن نشنیده است.

این امر به ویژه در امور مالی، به ویژه در این زمینه ها مهم است:

بدهی اوراق بهادار
گزینه های قابل معامله در بورس
معاوضه های پیش فرض اعتبار
اوراق بهادار مشتقه خارج از بورس

در این مقاله، خواهید آموخت که چرا معادله بلک-اسکولز در امور مالی بسیار مهم است، چه مشکلاتی را حل می کند و صنایعی که ایجاد کرده است.

در اینجا چیزی است که ما پوشش خواهیم داد:

پیش نیاز دانش مالی
قیاس: قیمت بلیط کنسرت را پیش بینی کنید
توضیح انگلیسی ساده با مثال کد
مفاهیم در دنیای واقعی

توجه: در مثال کد، ما با گزینه های call and put اروپایی کار خواهیم کرد.

پیش نیاز دانش مالی

برای استفاده بیشتر از این مقاله و درک معادله بلک اسکولز، فقط باید بدانید چه چیزی مشتقات مالی و گزینه ها در امور مالی هستند.

اساساً مشتقات مالی ابزار هستند سرمایه گذاران برای مدیریت ریسک و بهبود بازده استفاده می کنند.

انواع مختلفی از مشتقات مالی وجود دارد. یکی از این گزینه ها گزینه نام دارد.

گزینه ها مانند انتخاب های مالی هستند با آپشن‌ها، می‌توانید حق خرید یا فروش چیزی را در زمان و قیمت مشخصی دریافت کنید، اما فقط در صورت تمایل.

ایده اصلی این است که آنها به مدیریت ریسک کمک می کنند تا بتوانید در آینده سرمایه گذاری های بهتری انجام دهید.

قیاس: قیمت بلیط یک کنسرت را پیش بینی کنید

تصور کنید قصد دارید برای یک کنسرت بلیط بخرید.

قیمت بلیط بسته به تغییر است روی محبوبیت هنرمند، تقاضا و زمان تا کنسرت.

بسته به روی که، بهترین تصمیم ممکن را برای خرید بلیط با کمترین قیمت می گیرید.

همانطور که در مورد آن فکر می کنید خطر سرمایه گذاران با خرید انبوه در یک زمان خاص، از معادله بلک شولز برای تخمین ارزش منصفانه مشتقات مالی استفاده می کنند.

به این ترتیب، آنها مطمئن می شوند که انتخاب های عاقلانه ای برای سرمایه گذاری در بازارهای همیشه در حال تغییر دارند.

Black-Scholes به زبان انگلیسی ساده – با مثال کد

کاریکاتور برندگان جایزه نوبل فیشر بلک، مایرون اسکولز و رابرت مرتون

اساساً معادله بلک شولز مشکل روش قیمت گذاری صحیح گزینه ها در بازارهای مالی را حل کرد.

این بسیار مهم است، زیرا به بانک ها و مؤسسات مالی کمک می کند تا به طور مؤثر ریسک را مدیریت کنند.

با این حال، همیشه اینطور نبود. قبل از سال 1973، زمانی که معادله ایجاد شد (سازندگان آن برنده جایزه نوبل شدند)، تعیین قیمت گزینه ها بسیار پیچیده تر و دشوارتر بود.

قبل از ایجاد بلک شولز معادله، یک روش ریاضی استاندارد برای پیش‌بینی قیمت گزینه‌ها وجود نداشت.

معامله گران اغلب متکی بودند روی تجربه شخصی و شرایط بازار، که منجر به قیمت های غیرقابل اطمینان گزینه شد.

و روش های ریاضی قبلی به طور کامل عواملی مانند نوسانات، زوال زمانی و نرخ بهره را در نظر نمی گرفتند. بنابراین هنگام قیمت گذاری گزینه ها خطاهای زیادی وجود داشت.

پیشنهاد می‌کنیم بخوانید: راهنمای دیکشنری ها در پایتون

معادله بلک اسکولز در اینجا آمده است:

معادله بلک اسکولز

$$\frac{\partial V}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} = rV – r S \frac{\partial V}{\جزئی S}$$

معادله بلک اسکولز

در حالی که ما به خود معادله خیلی عمیق نگاه نمی کنیم، اجزای اصلی و مفاهیم آن را تشریح خواهیم کرد.

اساساً، معادله بلک-اسکولز چگونگی تغییر ارزش یک گزینه را بر اساس زمان پیش‌بینی می‌کند روی چندین متغیر:

V – قیمت اختیار معامله به عنوان تابعی از قیمت سهام اس و زمان تی
S – قیمت دارایی پایه
t – زمان
σ – نوسانات
r – نرخ بهره.

سمت چپ معادله توضیح می دهد که چگونه ارزش گزینه در طول زمان تغییر می کند و چگونه فراز و نشیب های بازار بر آن تأثیر می گذارد.

سمت راست معادله نشان می دهد که چگونه ارزش گزینه به دلیل نرخ بهره افزایش می یابد و چگونه تغییرات در قیمت دارایی بر آن تأثیر می گذارد.

با مساوی کردن این دو طرف، قیمت منصفانه گزینه را مشخص می کنیم.

مثال کد پایتون

در این مثال کد، بر اساس را پیدا خواهیم کرد روی بسیاری از پارامترها، ارزش نظری بازار یک گزینه.

برای مثال ما، بیایید موارد زیر را فرض کنیم:

قیمت فعلی سهام (S) = 100 دلار. این قیمت سهام در حال حاضر است.
قیمت اعتصاب (K) = 105 دلار. این قیمت خاصی است که دارنده اختیار معامله می تواند دارایی پایه را در آن بخرد (تماس بگیرد) یا بفروشد (قرار دهد).
زمان تا انقضا (T) = 1 سال (یا 1.0 زمانی که بر حسب سال بیان شود). این زمان باقی مانده تا پایان گزینه است.
نرخ بهره بدون ریسک (r) = 0.05% (یا 0.0005 هنگامی که به صورت اعشاری بیان می شود). این نرخ بهره است روی سرمایه گذاری بدون ریسک
نوسانات (سیگما) = 20% (یا 0.2 هنگامی که به صورت اعشاری بیان می شود). انتظار می رود قیمت سهام تا چه اندازه نوسان داشته باشد.

from blackscholes import BlackScholesCall, BlackScholesPut

def calculate_option_prices(S, K, T, r, sigma, q):
    """
    Calculate the Black-Scholes option prices for European call and put options using the 'blackscholes' package.

    Parameters:
    S : float - current stock price
    K : float - strike price of the option
    T : float - time to maturity (in years)
    r : float - risk-free interest rate (annual as a decimal)
    sigma : float - volatility of the underlying stock (annual as a decimal)
    q : float - annual dividend yield (as a decimal)

    Returns:
    tuple - (call price, put price)
    """
    # Creating instances of BlackScholesCall and BlackScholesPut
    call_option = BlackScholesCall(S=S, K=K, T=T, r=r, sigma=sigma, q=q)
    put_option = BlackScholesPut(S=S, K=K, T=T, r=r, sigma=sigma, q=q)

    # Get call and put prices
    call_price = call_option.price()
    put_price = put_option.price()

    return call_price, put_price


call_price, put_price = calculate_option_prices(100, 105, 1, 0.0005, 0.20, 0.0)
print("Call Price: {:.6f}, Put Price: {:.6f}".format(call_price, put_price))

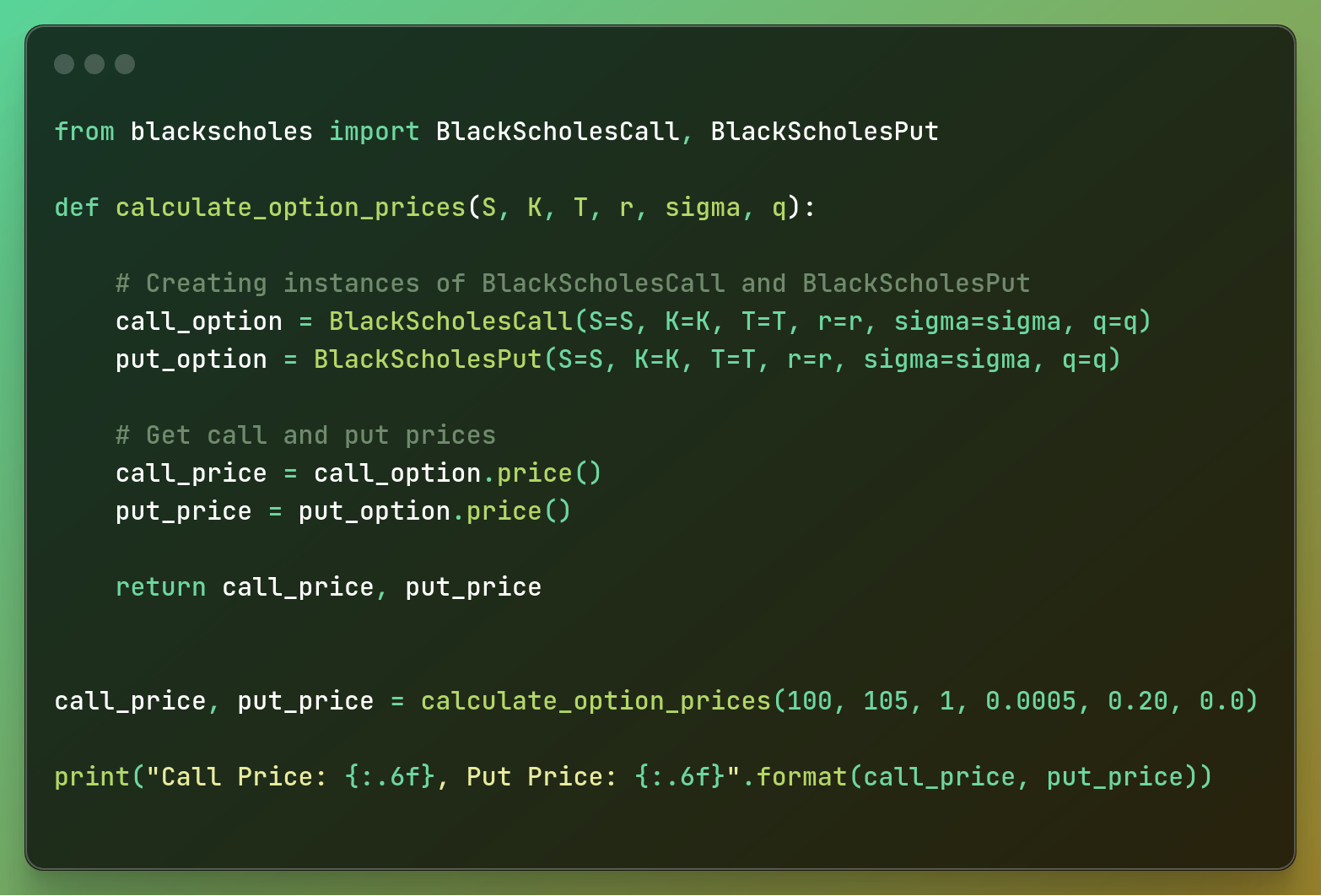
حالا بیایید کد را دقیق تر بررسی کنیم و ببینیم واقعاً چه اتفاقی می افتد روی اینجا:

مرحله 1: وارد کردن کتابخانه

این کتابخانه Python است که ما در این مقاله از آن استفاده می کنیم:

from blackscholes import BlackScholesCall, BlackScholesPut

مرحله 2: تابع محاسبه قیمت گزینه ها را ایجاد کنید

در کد زیر تابعی را که برای محاسبه فراخوانی گزینه ها و قرار دادن قیمت ها نیاز داریم وارد می کنیم.

def calculate_option_prices(S, K, T, r, sigma, q):

    call_option = BlackScholesCall(S=S, K=K, T=T, r=r, sigma=sigma, q=q)
    put_option = BlackScholesPut(S=S, K=K, T=T, r=r, sigma=sigma, q=q)

    call_price = call_option.price()
    put_price = put_option.price()

    return call_price, put_price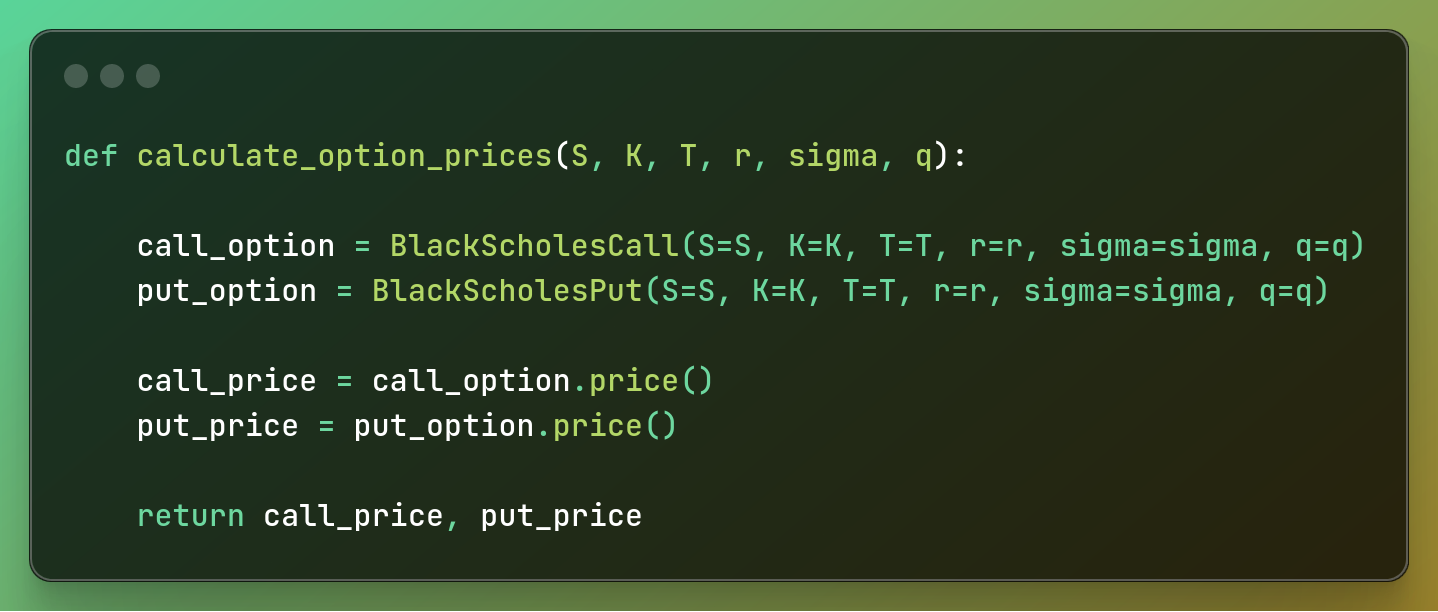

پارامترهای اصلی تابع عبارتند از:

S: شناور – قیمت فعلی سهام
K : شناور – قیمت اعتصاب گزینه
T: شناور – زمان تا سررسید (به سال)
r: نرخ بهره شناور – بدون ریسک (سالانه به صورت اعشاری)
سیگما: شناور – نوسانات سهام پایه (سالانه به صورت اعشاری)
q : شناور – بازده سود سالانه (به صورت اعشاری)

پیشنهاد می‌کنیم بخوانید: راهنمای مقدماتی برایتون

و برمیگرده:

تاپل – (قیمت تماس، قیمت قرار دادن)

ابتدا گزینه های فراخوانی را محاسبه کرده و قرار می دهیم. سپس قیمت را از آن استخراج می کنیم. همچنین می‌توانیم ویژگی‌های دیگری مانند جذابیت یا دلتای این قراردادهای مالی را با توجه به مستندات کتابخانه به دست آوریم.

مرحله 3: قیمت گزینه ها را محاسبه کنید

قیمت خرید و فروش یک اختیار خرید، هزینه های خرید قراردادهای اختیار مربوطه است.

call_price, put_price = calculate_option_prices(100, 105, 1, 0.0005, 0.20, 0.0)
print("Call Price: {:.6f}, Put Price: {:.6f}".format(call_price, put_price))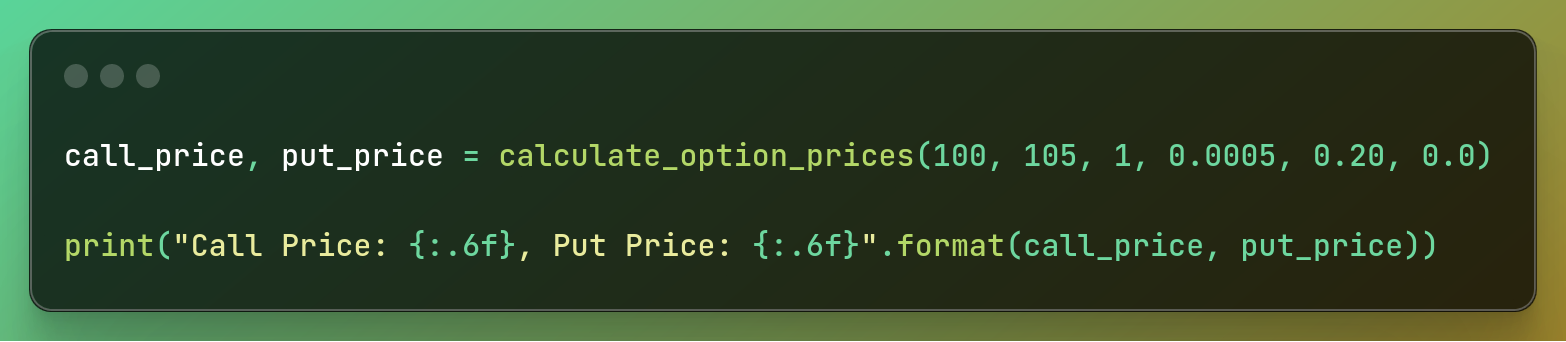

ما به عنوان مثال استفاده می کنیم:

قیمت سهام فعلی: 100 دلار
قیمت پیشنهادی: 105 دلار
مدت زمان بلوغ: 1 سال
نرخ بهره بدون ریسک: 0.05% (به صورت اعشاری: 0.0005)
نوسانات: 20% (به صورت اعشاری: 0.20)
بازده سود سهام: 0%

مستقر روی این عوامل، ما قیمت گذاری می کنیم:

قیمت گزینه تماس: 5.924799
قیمت گزینه قرار دهید: 10.872312

به این معنی که با توجه به این پارامترها:

قیمتی که در آن حق خرید دارید، اما نه تعهد، 5.924799 دلار است.
قیمتی که شما حق فروش آن را دارید، اما نه تعهدی، 10.872312 دلار است.

مفاهیم در دنیای واقعی

کاریکاتور رابطه دنیای واقعی با امور مالی

این معادله تاثیر زیادی در دنیای مالی داشته است.

در زیر برخی از صنایعی که معادله بلک شولز به شدت تغییر کرده است آورده شده است:

بدهی اوراق بهادار

به عبارت ساده، بدهی اوراق بهادار به تبدیل وام به چیزی قابل خرید و فروش اشاره دارد.

معادله بلک شولز روش قیمت گذاری بدهی های گروه بندی شده توسط بانک ها را مانند وام مسکن تغییر داد.

قبل از معادله بلک اسکولز، دانستن ارزش این بدهی ها بسیار سخت بود. اما با این معادله، بانک ها می توانند ارزش خود را خیلی بهتر درک کنند. این امر خرید و فروش این بدهی‌ها را آسان‌تر کرد و در عین حال از مزایا و خطرات احتمالی آن آگاه بود.

به این ترتیب، بازار این بدهی های وام مسکن رشد کرد. که به نوبه خود به رشد بازار مسکن کمک کرد.

گزینه های معامله شده در بورس

گزینه های معاملاتی یک تجارت بسیار نامطمئن بود. هیچ راهی وجود نداشت که واقعا بدانیم چگونه آنها را به درستی قیمت گذاری کنیم.

با این حال، با معادله Black-Scholes، قیمت گذاری گزینه بسیار آسان تر شد. به مردم این امکان را می داد که یک گزینه را بر اساس محاسبه کنند روی قیمت یک دارایی اساسی، نوسانات، زمان تا انقضا، و نرخ بهره.

دقت جدید به رشد بازار آپشن ها کمک کرد.

معاوضه های پیش فرض اعتباری

معاوضه های پیش فرض اعتباری مانند بیمه نامه های وام هستند. با پیش فرض اعتبار swap، اگر وام گیرنده نتواند بازپرداخت کند از شما محافظت می شود.

سوآپ های نکول اعتباری در مدیریت ریسک اعتباری بسیار مهم هستند. اما تنها پس از ایجاد معادله سیاه اسکولز بود که قیمت گذاری دقیق آنها انجام شد.

به این ترتیب، سوآپ های نکول اعتباری به ابزار بسیار مهمی برای موسسات مالی برای مدیریت ریسک مالی تبدیل شد.

اوراق بهادار مشتقه خارج از بورس

مشتقات خارج از بورس (OTC) معاملات خصوصی هستند که بین دو طرف بدون بورس اوراق بهادار انجام می شود.

قبل از بلک شولز، مذاکره در مورد شرایط و قیمت مشتقات فرابورس بسیار سخت بود. اما سپس معادله بلک شولز یک روش استاندارد برای یافتن قیمت مشتقات ارائه کرد.

این امر به فعالان بازار اجازه داد تا قراردادها را کارآمدتر و دقیق تر مذاکره کنند.

نتیجه

معادله بلک اسکولز به ایجاد دقت بیشتر در روش قیمت گذاری برخی چیزها کمک کرد.

این دقت به ایجاد نهادهای با ثبات تر کمک کرد، که به نوبه خود به ایجاد اقتصاد مقاومتی تر کمک کرد.

اگر علاقه مند به یادگیری بیشتر هستید، این ویدیو را ببینید:

https://www.youtube.com/watch؟v=A5w-dEgIU1M

اگر علاقه مند به کسب اطلاعات بیشتر در مورد امور مالی هستید:

کد کامل

منتشر شده در 1403-06-17 23:57:08

امتیاز شما به این مطلب