چگونه یک سیستم کنترل موشک بسازیم: نظریه کنترل پایه با پایتون

ساخت هر سیستم کنترلی، از جمله سیستم کنترل موشک، شامل ترکیب تئوری کنترل با برنامه نویسی است.

تئوری کنترل مطالعه این است که چگونه می توان سیستم ها را با استفاده از ورودی ها به شیوه ای مطلوب رفتار کرد.

هواپیماها، ماشین‌ها، قطارها، مدارها، موشک‌ها و بسیاری از سیستم‌های دیگر باید مغز یا معماری درون خود داشته باشند.

تئوری کنترل مطالعه معماری های کنترل این سیستم های پیچیده است.

در این مقاله، روش اعمال نظریه کنترل برای ایجاد یک سیستم کنترل موشک با استفاده از پایتون را بررسی خواهیم کرد.

این یک راهنمای ساده برای چگونگی ایجاد معماری سیستم های پیچیده است. در این مورد، آن را بر اساس روی یک موشک

در این مقاله با موارد زیر آشنا خواهید شد:

• سیستم های موشک و پخت کیک: مقایسه ای سرگرم کننده
• کنترل موشک ساده شده: درک کنترلرهای PID
• مثال کد: طراحی یک کنترلر ساده PID
• نتیجه گیری: سیستم های کنترل غیر خطی

توجه داشته باشید: ما فرض می کنیم که موشک تغییرناپذیر زمان است، به این معنی که رفتار آن در طول زمان تغییر نمی کند. پرداختن به پویایی های متغیر با زمان، این آموزش را بیش از آنچه من می خواهم پیچیده می کند.

سیستم های موشک و پخت کیک: مقایسه ای سرگرم کننده

سیستم کنترل موشک چیست؟

تصور کنید در حال حمایت از یک کیک هستید. دستور پخت شما مراحل و مواد لازم برای پخت کیک را ارائه می دهد.

در این قیاس:

• کیک همان موشک است
• دستور العمل برنامه پرواز موشک است
• اقدامات نانوا سیستم کنترل موشک است

همانطور که دمای فر یا زمان مخلوط کردن را تغییر می دهید تا بهترین کیک را بدست آورید، یک سیستم کنترل پارامترهای موشک را برای اطمینان از ماندگاری آن تغییر می دهد. روی روند خود را ادامه می دهد و ثابت می ماند.

چرا سیستم های کنترل در برنامه نویسی مهم هستند؟

با درک سیستم های کنترل، در طراحی الگوریتمی و تفکر سیستمی بهتر خواهید شد.

همچنین شما را قادر می سازد تا روش تنظیم فرآیندها در حلقه های بازخورد را بیابید. این در بسیاری از زمینه های برنامه نویسی بسیار مهم است.

شما عمدتاً از تئوری کنترل و سیستم های کنترل هنگام ایجاد نرم افزار برای موارد زیر استفاده خواهید کرد:

• رباتیک و اتوماسیون: سیستم های کنترل حرکت دقیق و سازگاری را در روبات ها با استفاده از حلقه های بازخورد بر اساس امکان پذیر می کنند روی ورودی سنسور
• پردازش سیگنال و ارتباطات: انتقال داده ها، تصحیح خطا و فیلتر کردن را برای ارتباطات قابل اعتماد بهینه می کنند.
• سیستم های جاسازی شده و اینترنت اشیا: سیستم های کنترل تعاملات دستگاه با محیط ها را مدیریت می کنند، ورودی های حسگر را پردازش می کنند و خروجی ها را به طور موثر تنظیم می کنند.

روش ایجاد یک سیستم کنترل موشک

از نظر قیاس پخت کیک ما:

1. کیک و دستور غذا را انتخاب کنید: یک استراتژی کنترلی ساده، مانند انتخاب دستور پخت کیک پایه، انتخاب کنید. یک انتخاب رایج کنترل کننده PID است زیرا ساده و موثر است.
2. درک مواد تشکیل دهنده: یک مدل ریاضی از مشخصات و مسیر حرکت موشک استخراج کنید. مانند مطالعه دستور غذا و مواد تشکیل دهنده. به این ترتیب، ما درک روشنی از سیستم به دست می آوریم.
3. جمع آوری مواد اولیه: پارامترهای اولیه را مانند جمع آوری مواد اولیه خود تنظیم کنید.
4. مخلوط کردن و پخت: سیستم را تنظیم و آزمایش کنید، دقیقاً مانند مخلوط کردن مواد و پخت. این شامل استفاده از نمودارهای مختلف برای بررسی ثبات و عملکرد است.
5. افزودن لمس نهایی: پارامترها را درست مانند افزودن تزئینات نهایی به کیک خود تنظیم کنید تا سیستم کنترل را برای کارایی بهینه کنید.
6. دنبال دستور غذا: طرح خود را به شکلی کاربردی تبدیل کنید، مانند پیروی از دستور کیک.

کنترل موشک ساده شده: درک کنترلرهای PID

یک سیستم کنترل ساده: کنترل کننده PID

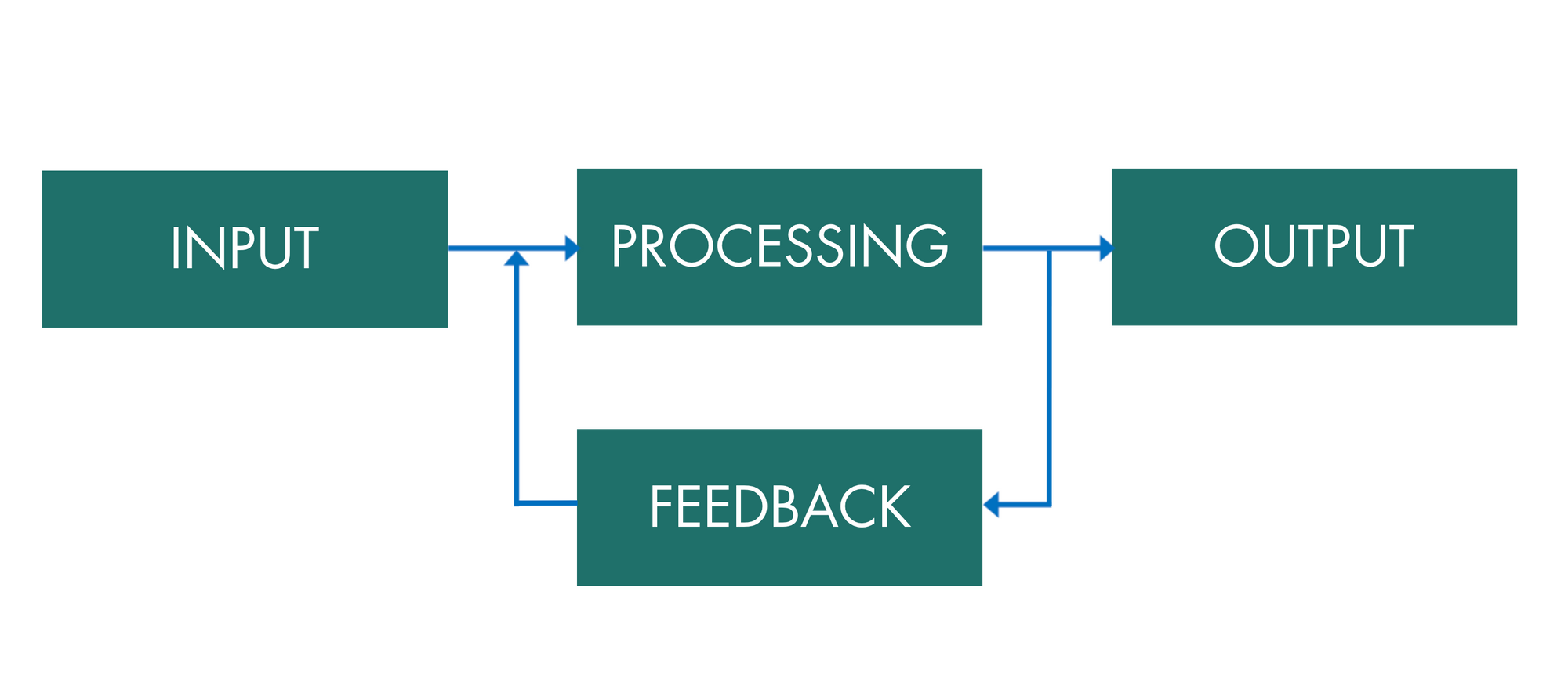
هر سیستم کنترلی یک کنترلر دارد که آن را اجرا می کند. یکی از پرکاربردترین کنترلرها، کنترلر PID است.

در مثال کد اینجا، از کنترلر PID استفاده خواهیم کرد. این به این دلیل است که برای سیستم های کنترل ساده ساده و موثر است.

در یک سیستم کنترل موشک، کنترل کننده PID موشک به طور مداوم مسیر موشک (بلوک پردازش) را با مقایسه موقعیت فعلی آن با جایی که باید باشد (بلوک بازخورد) تنظیم می کند.

به این ترتیب موشک می ماند روی سیر کرده و به مقصد نهایی خود می رسد.

کنترل کننده PID دارای سه بخش کلیدی است که در بخش پردازش و بازخورد سیستم کار می کنند: بهره متناسب (Kp)، بهره انتگرال (Ki) و بهره مشتق (Kd).

• بهره متناسب (Kp): به هر خطایی فوراً واکنش نشان می‌دهد و باعث می‌شود که سیستم به سرعت پاسخ دهد، اما گاهی اوقات باعث می‌شود که هدف را بیش از حد مجاز کند.
• بهره انتگرال (Ki): خطاهای گذشته را با اضافه کردن آنها در طول زمان برطرف می کند و از شر خطاهای باقی مانده خلاص می شود، اما در صورت تنظیم بیش از حد بالا می تواند سیستم را ناپایدار کند.
• بهره مشتق (Kd): خطاهای آینده را پیش‌بینی می‌کند تا به جلوگیری از بیش از حد و هموار کردن پاسخ سیستم کمک کند.

به همین دلیل است که به آن یک کنترل کننده PID (Proportional-Integral-Derivative) می گویند.

این سه قسمت با هم کار می کنند تا یک سیگنال کنترلی ایجاد کنند که تنظیمات موشک را تغییر می دهد. این تضمین می کند که پایدار، دقیق و موثر است.

با کنترلر PID، می‌توانیم روش تغییر موقعیت و سرعت ورودی‌هایی مانند رانش و ارتفاع را کنترل کنیم تا مطمئن شویم موشک پایدار است و روی مسیر مورد نظر آن

تجزیه و تحلیل ثبات

طراحی یک کنترلر PID به معنای طراحی یک سیستم کنترل پایدار است.

این process به طراحی یک سیستم کنترل پایدار، آنالیز پایداری می گویند.

روش‌های زیادی وجود دارد، اما در مثال کد از آن استفاده خواهیم کرد:

• جایگاه ریشه: ثبات و پاسخ سیستم را نشان می دهد
• نمودار بود: سیستم را نمایش می دهد کسب کردن و حاشیه فاز
• طرح نایکیست: ثبات و نوسانات بالقوه را نشان می دهد

در این حالت، بهره و حاشیه فاز به سادگی به این معنی است که سیستم کنترل می تواند تغییرات را تحمل کند.

حاشیه سود به ما می گوید که چقدر سود سیستم می تواند بدون از دست دادن ثبات افزایش یابد. Gain یعنی چقدر سیگنال ورودی را تقویت کنیم تا سیگنال خروجی تولید شود.

حاشیه فاز به ما می گوید که چقدر تاخیر بدون از دست دادن ثبات قابل تحمل است. تأخیر در تئوری کنترل به این معنی است که چه مدت زمان طول می کشد تا خروجی به ورودی پاسخ دهد.

این به ما می گوید که چگونه Kp، Ki و Kd را تغییر دهیم تا کنترل کننده PID بتواند موشک را به شیوه ای موثر کنترل کند.

نیاز به توابع انتقال: کنترل موشک و تعیین مقادیر اجزا

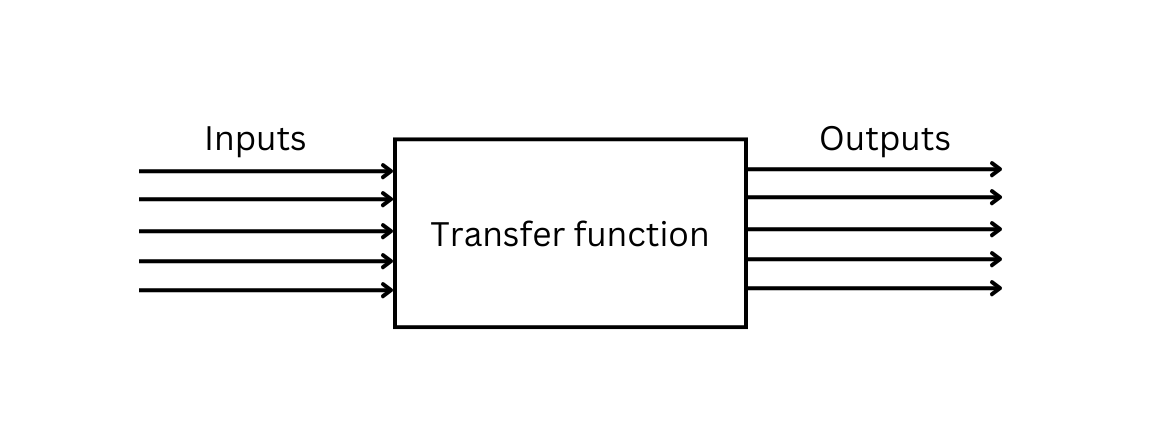
برای پیاده سازی هر سیستم کنترلی، به دو تابع انتقال نیاز داریم: یکی نظری و دیگری فیزیکی.

توابع انتقال به ما می گویند که چگونه ورودی ها به صورت ریاضی به خروجی تبدیل می شوند.

تابع نظری، در این مورد، کنترل کننده PID است.

تابع انتقال سیستم فیزیکی نشان دهنده دینامیک دنیای واقعی و رفتار اجزای فیزیکی در سیستم است.

با ترکیب هر دو، ما می توانیم رفتار مواد و مقادیر اجزاء مانند:

• مقادیر خازن برای ذخیره انرژی
• مقادیر کالیبراسیون سنسور برای اندازه گیری دقیق داده ها و بازخورد
• ثابت های فنری برای سیستم های جذب شوک
• رتبه بندی فشار برای مخازن سوخت و اکسید کننده

به این ترتیب، کنترل کننده PID نه تنها مغز موشک است، بلکه می تواند مقادیر اجزای مورد نیاز را به ما بگوید تا موشک بتواند مسیر خود را طی کند.

مهندسان چگونه معادله تابع انتقال فیزیکی را پیدا می کنند؟

ابتدا باید بفهمیم که موشک برای چیست.

آیا ماهواره LEO (مدار پایین زمین) یا MEO (مدار متوسط ​​زمین) را به فضا می فرستد یا موشکی را به ماه؟

پس از دانستن کاربرد آن، می‌توانیم با ریاضی و فیزیک معادله فیزیکی تابع انتقال را پیدا کنیم.

در واقع یک رشته مهندسی کامل به نام وجود دارد شناسایی سیستم اختصاص داده شده به این.

حال بیایید ببینیم که چگونه برای هر سیستم کنترلی، عملکرد انتقال فیزیکی آن را پیدا کنیم.

مثال کد: طراحی یک کنترلر ساده PID

حالا با این مثال کد، یک سیستم کنترل ساده برای موشک ایجاد می کنیم.

قبل از اینکه وارد کد شویم، بیایید در مورد دسی بل صحبت کنیم.

دسی بل از مقیاس لگاریتمی برای اندازه گیری صدا استفاده می کند. در تئوری کنترل، آنها سود را به گونه ای اندازه گیری می کنند که تجسم آسان تر باشد روی نمودارها

به این ترتیب، ما می توانیم مقادیر بزرگ و کوچک بیشتری را در یک محدوده قابل مدیریت ببینیم.

به عبارت دیگر، با دیدن بهره در مقیاس لگاریتمی، می‌بینیم که ورودی چقدر تقویت می‌شود تا خروجی در یک محدوده قابل مدیریت از مقادیر باشد.

روش آن را هم توضیح خواهم داد root لوکوس، نمودار Bode، و نمودار نایکیست به مهندسان در تجزیه و تحلیل پایداری کمک می کنند.

بیایید کد را ببینیم – و سپس آن را بلوک به بلوک تجزیه و تحلیل می کنیم:

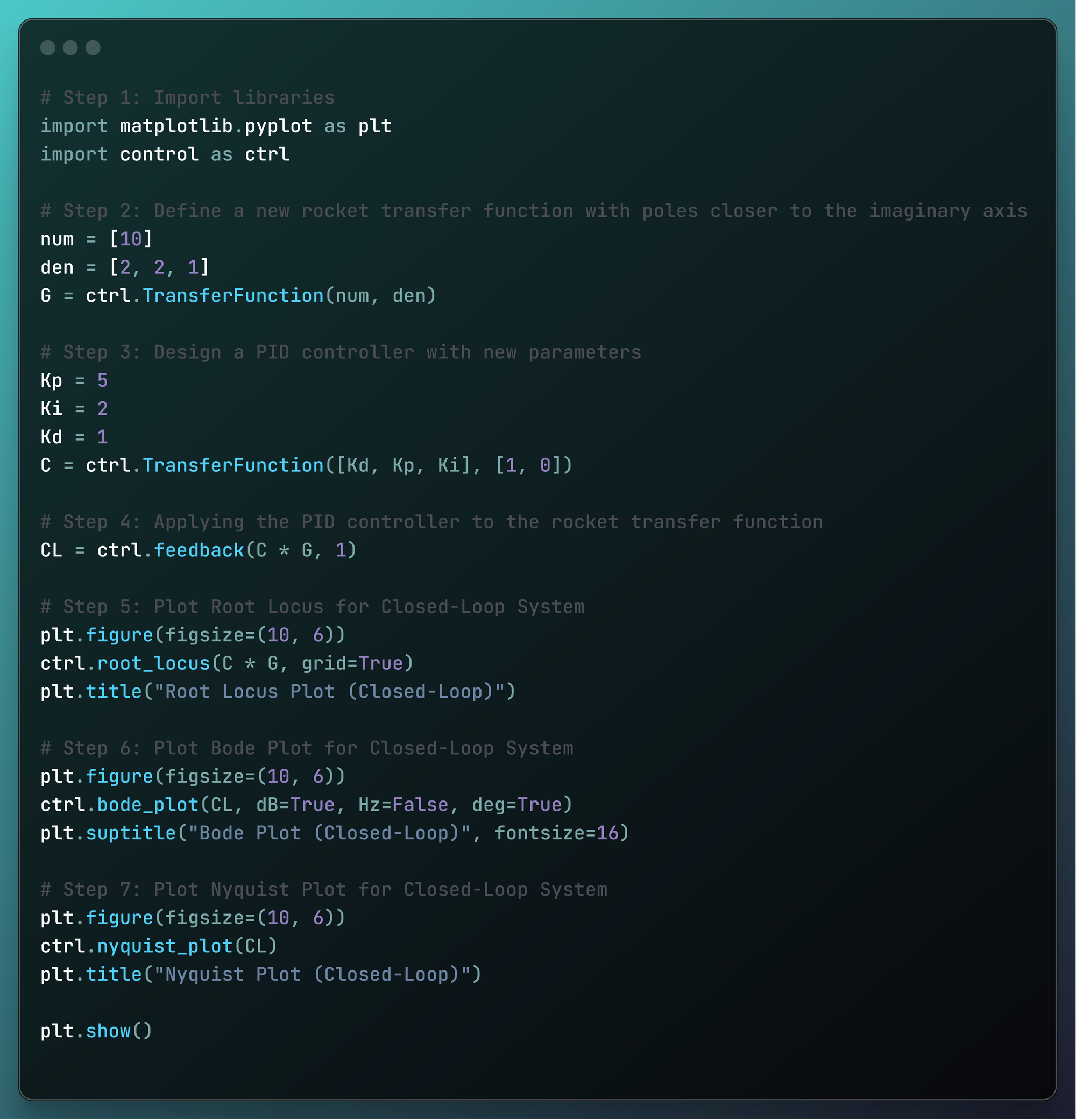
# Step 1: Import libraries
import matplotlib.pyplot as plt
import control as ctrl

# Step 2: Define a new rocket transfer function with poles closer to the imaginary axis
num = [10] 
den = [2, 2, 1] 
G = ctrl.TransferFunction(num, den)

# Step 3: Design a PID controller with new parameters
Kp = 5
Ki = 2
Kd = 1
C = ctrl.TransferFunction([Kd, Kp, Ki], [1, 0])

# Step 4: Applying the PID controller to the rocket transfer function
CL = ctrl.feedback(C * G, 1)

# Step 5: Plot Root Locus for Closed-Loop System
plt.figure(figsize=(10, 6))
ctrl.root_locus(C * G, grid=True)
plt.title("Root Locus Plot (Closed-Loop)")

# Step 6: Plot Bode Plot for Closed-Loop System
plt.figure(figsize=(10, 6))
ctrl.bode_plot(CL, dB=True, Hz=False, deg=True)
plt.suptitle("Bode Plot (Closed-Loop)", fontsize=16)

# Step 7: Plot Nyquist Plot for Closed-Loop System
plt.figure(figsize=(10, 6))
ctrl.nyquist_plot(CL)
plt.title("Nyquist Plot (Closed-Loop)")

plt.show()

مرحله 1: وارد کردن کتابخانه ها

import matplotlib.pyplot as plt
import control as ctrl

ما اینجاییم import دو کتابخانه:

• matplotlib: یک کتابخانه رسم برای ایجاد انواع مختلف تجسم
• کنترل: کتابخانه ای برای تجزیه و تحلیل و طراحی سیستم های کنترل

مرحله 2: عملکرد انتقال سیستم موشک را تعریف کنید

num = [10] 
den = [2, 2, 1] 
G = ctrl.TransferFunction(num, den)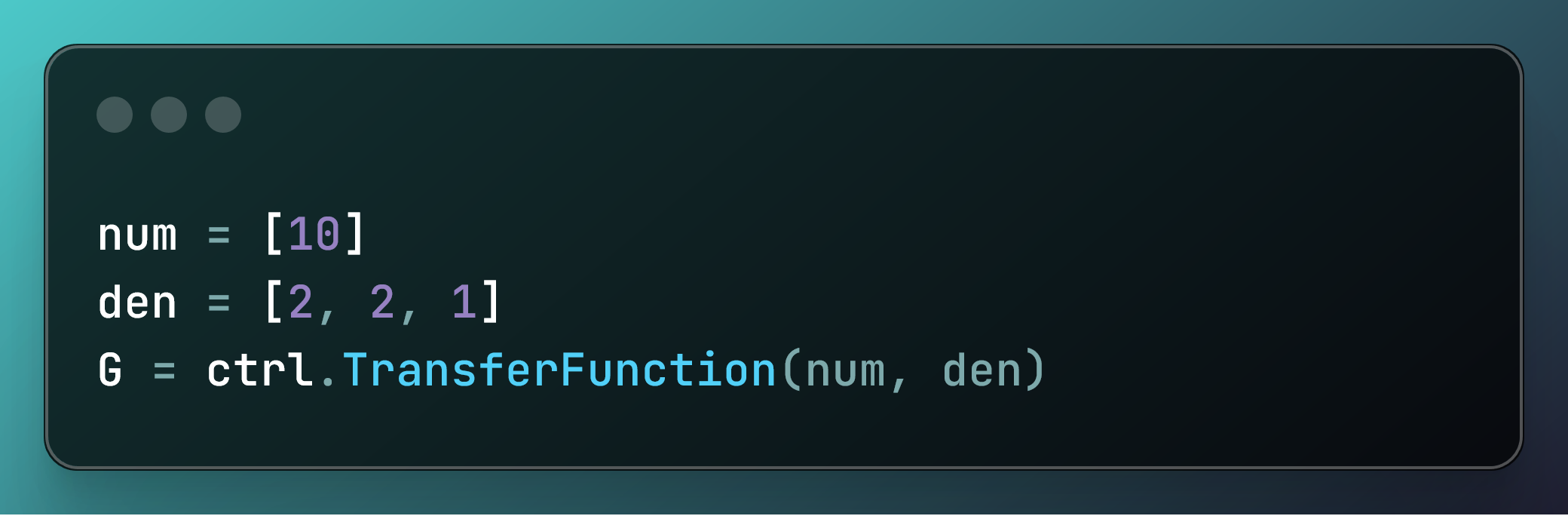

در این کد تابع انتقال سیستم فیزیکی را تعریف می کنیم

• num=[10]: بهره سیستم را روی 10 تنظیم می کند.
• den=[2,2,1]: مخرج را تعریف می کند.
• G = ctrl.transferFunction(num, cen): تابع انتقال را می سازد.

این تابع انتقالی است که می خواهیم با PID کنترل کنیم:

در این مثال کد، معادله موشک تابع انتقال بسیار ساده است. اما در زندگی واقعی، توابع انتقال موشک، سیستم های خطی تغییرناپذیر زمان نیستند. معمولاً آنها سیستم های غیرخطی بسیار پیچیده ای هستند.

مرحله 3: یک کنترلر PID با پارامترهای جدید طراحی کنید

Kp = 5
Ki = 2
Kd = 1
C = ctrl.TransferFunction([Kd, Kp, Ki], [1, 0])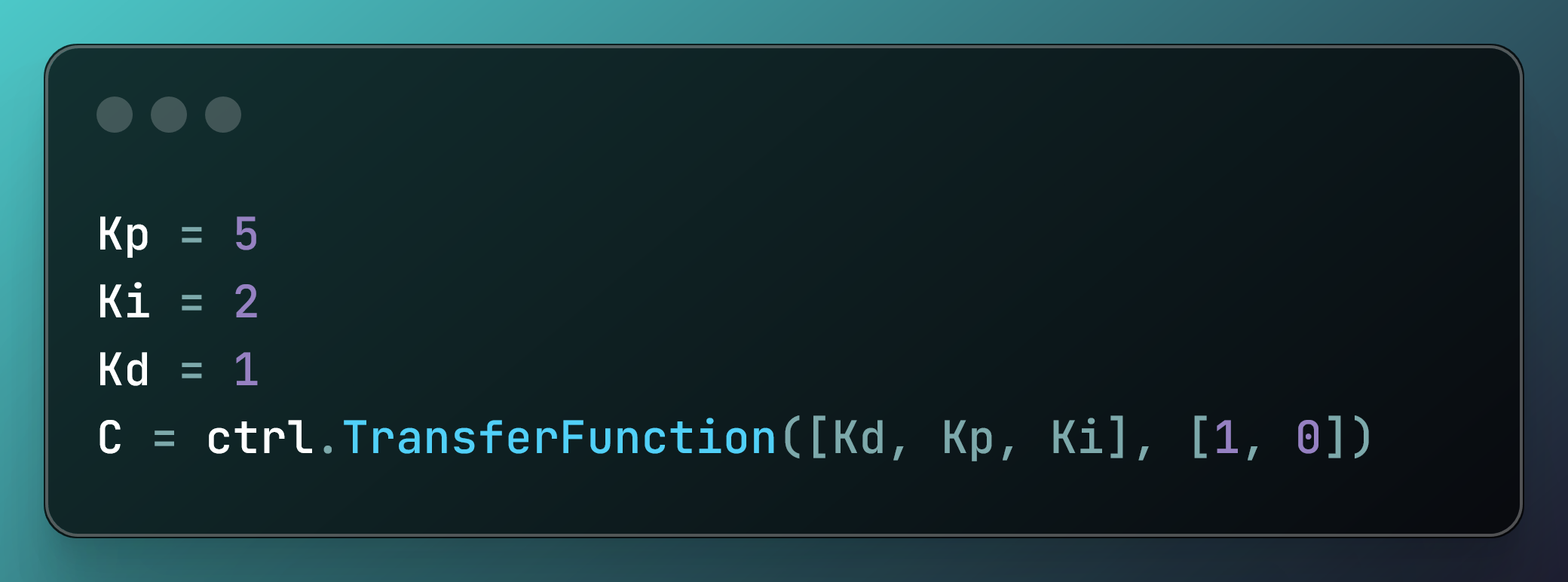

این کد یک کنترل کننده PID را با دستاوردهای خاص تنظیم می کند و یک تابع انتقال ایجاد می کند:

• Kp = 5: بهره متناسب را روی 5 تنظیم می کند.
• Ki = 2: بهره انتگرال را روی 2 تنظیم می کند.
• Kd = 1: بهره مشتق را روی 1 تنظیم می کند.
• C = ctrl.TransferFunction([Kd, Kp, Ki], [1, 0]): یک تابع انتقال از کنترلر PID ایجاد می کند

مرحله 4: اعمال کنترل کننده PID در عملکرد انتقال موشک

CL = ctrl.feedback(C * G, 1)

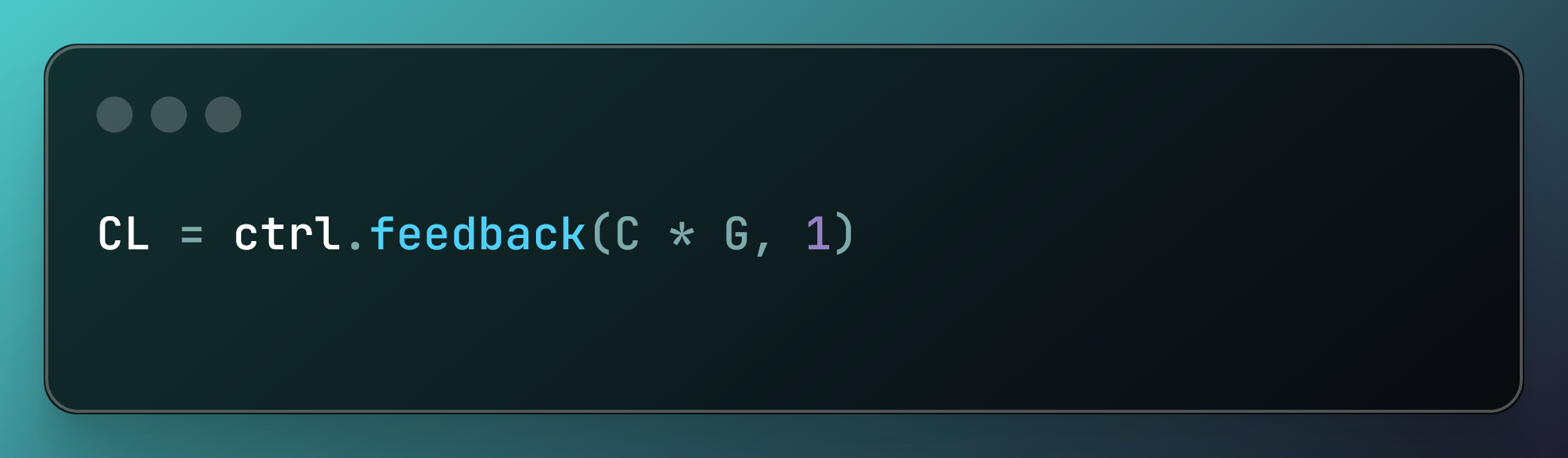
• C * G: کنترل کننده PID را ضرب می کند C با سیستم G (موشک) برای تشکیل تابع انتقال حلقه باز، که رفتار سیستم را بدون بازخورد و اتکا مدل می کند. روی تنظیمات از پیش تعریف شده
• ctrl.feedback(C * G, 1): تابع انتقال حلقه بسته را با اعمال بازخورد و نمایش رفتار سیستم با بازخورد محاسبه می کند. این به آن اجازه می دهد تا ورودی ها را تنظیم کند و به طور خودکار خطاها را تصحیح کند.
• CL: سیستم حلقه بسته حاصل را ذخیره می کند، کنترل کننده را با موشک یکپارچه می کند تا عملکرد مورد نظر را از طریق بازخورد حفظ کند، و برای تجزیه و تحلیل یا شبیه سازی بیشتر استفاده می شود.

مرحله 5: Root Locus برای تجزیه و تحلیل بهره

در این کد:

plt.figure(figsize=(10, 6))
ctrl.root_locus(C * G, grid=True)
plt.title("Root Locus Plot (Closed-Loop)")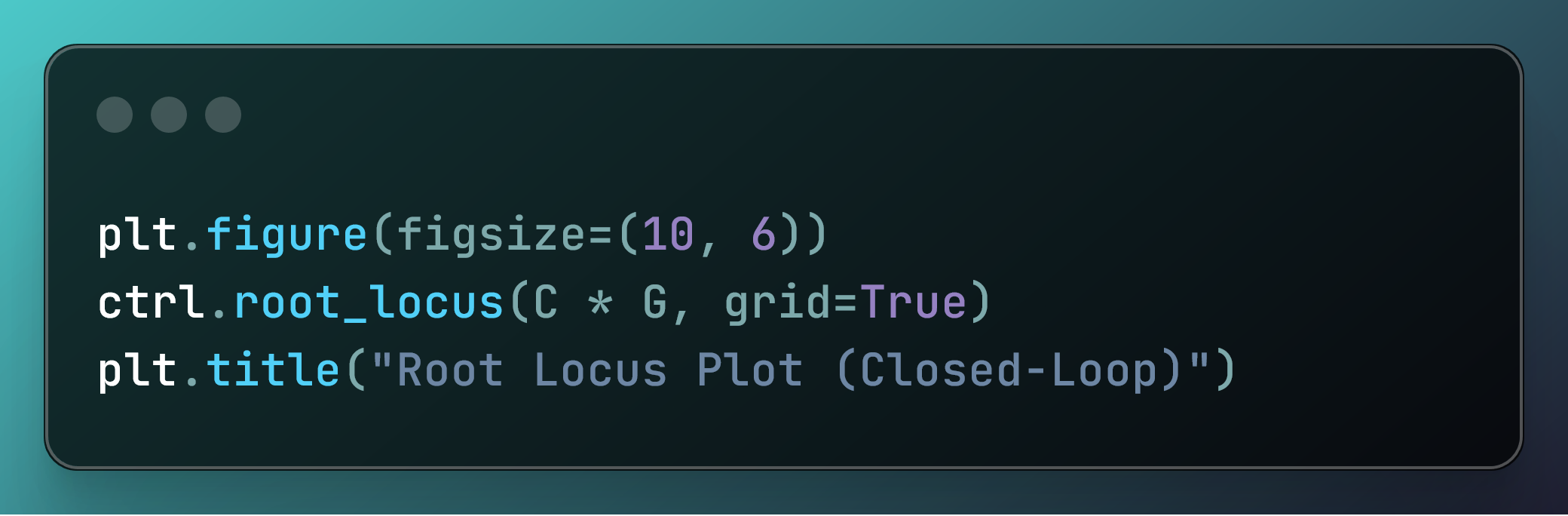

ما این طرح را ایجاد می کنیم:

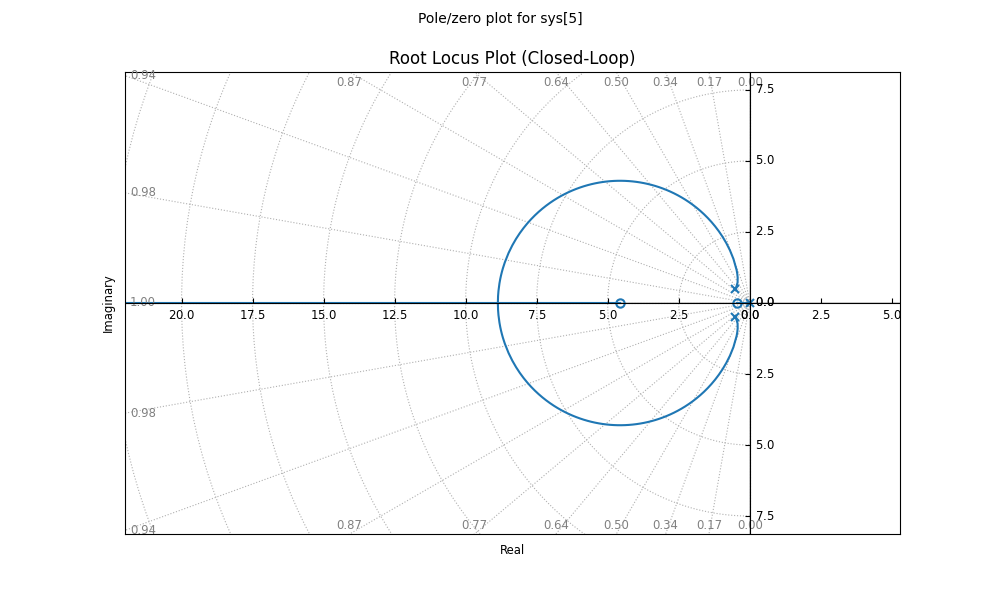
این یک است root نمودار مکان این برای کمک به مهندسان در مطالعه پایداری سیستم های کنترل اختراع شد.

صلیب ها روی نموداری که قطب نامیده می شود بسیار مهم است.

اگر آنها هستند روی در سمت چپ نمودار، سیستم پایدار است. اگر آنها هستند روی سمت راست، سیستم ناپایدار است.

هرچه بیشتر به سمت چپ باشند، سیستم سریع‌تر پس از یک اختلال به حالت عادی باز می‌گردد و بنابراین، پایدارتر خواهد بود.

اما حرکت بیشتر به سمت چپ بسته به این امر می تواند باعث نوسانات بسیار زیادی شود روی مکان های خاص آنها

نکته کلیدی این است:

• با تغییر در Kp، Ki، و Kd، این قطب ها را به سمت چپ حرکت می دهد تا جایی که ممکن است بدون ایجاد نوسان.

با این حال root نمودار مکان برای اطمینان از ثبات کافی نیست. ما باید از پلات Bode و Nyquist نیز استفاده کنیم. فقط با آنها می توانیم بهترین مقادیر کنترل کننده PID را برای سیستم کنترل موشک بدست آوریم.

مرحله 6: طرح اولیه برای تجزیه و تحلیل پایداری

در این کد:

plt.figure(figsize=(10, 6))
ctrl.bode_plot(CL, dB=True, Hz=False, deg=True)
plt.suptitle("Bode Plot (Closed-Loop)", fontsize=16)

ما این طرح را ایجاد می کنیم:

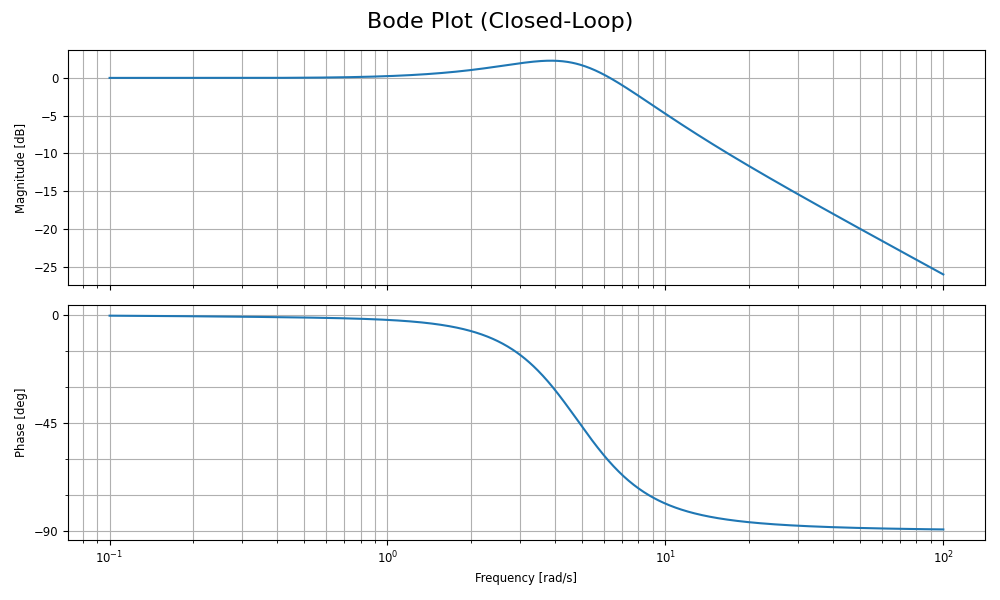
نمودار Bode برای کمک به مهندسان در درک چگونگی واکنش یک سیستم به تغییرات و پایداری آن در شرایط مختلف ابداع شد.

نمودار Bode همچنین پایداری و حاشیه ایمنی سیستم را نشان می دهد.

بیایید بفهمیم که چگونه کار می کند:

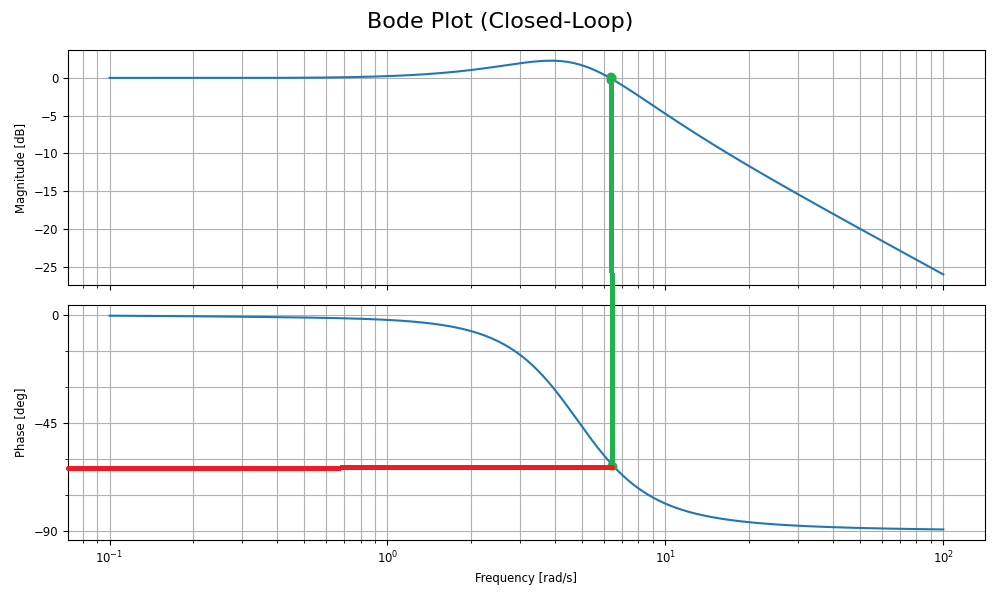
نمودار روی بالای آن نمودار بزرگی و زیر آن پلات فاز نامیده می شود.

نمودار بزرگی بهره یک سیستم را در فرکانس های مختلف اندازه گیری می کند. بهره بالاتر به معنای واکنش سریعتر و قوی تر است که برای کنترل دقیق خوب است.

نمودار فاز، تغییر فاز معرفی شده توسط سیستم را در فرکانس های مختلف اندازه گیری می کند. تغییر فاز زمانی دیده می شود که بهره 0 باشد.

در این حالت، با خط سبز می‌توانیم ببینیم چه زمانی بهره صفر است و چه تغییر فازی با آن در خط قرمز مرتبط است. تقریبا 63 درجه است.

یک محدوده ایده آل، تغییر فاز 30 تا 60 درجه است که ثبات و سرعت پاسخ را متعادل می کند.

بیش از 60 درجه، سیستم بسیار پایدار است، اما ممکن است واکنش سیستم به تغییرات را کاهش دهد.

بنابراین پس از تجزیه و تحلیل نمودار، می توان نتیجه گرفت که این کنترل کننده PID پایدار است.

مرحله 7: طرح Nyquist برای تجزیه و تحلیل ثبات

در این کد:

plt.figure(figsize=(10, 6))
ctrl.nyquist_plot(CL)
plt.title("Nyquist Plot (Closed-Loop)")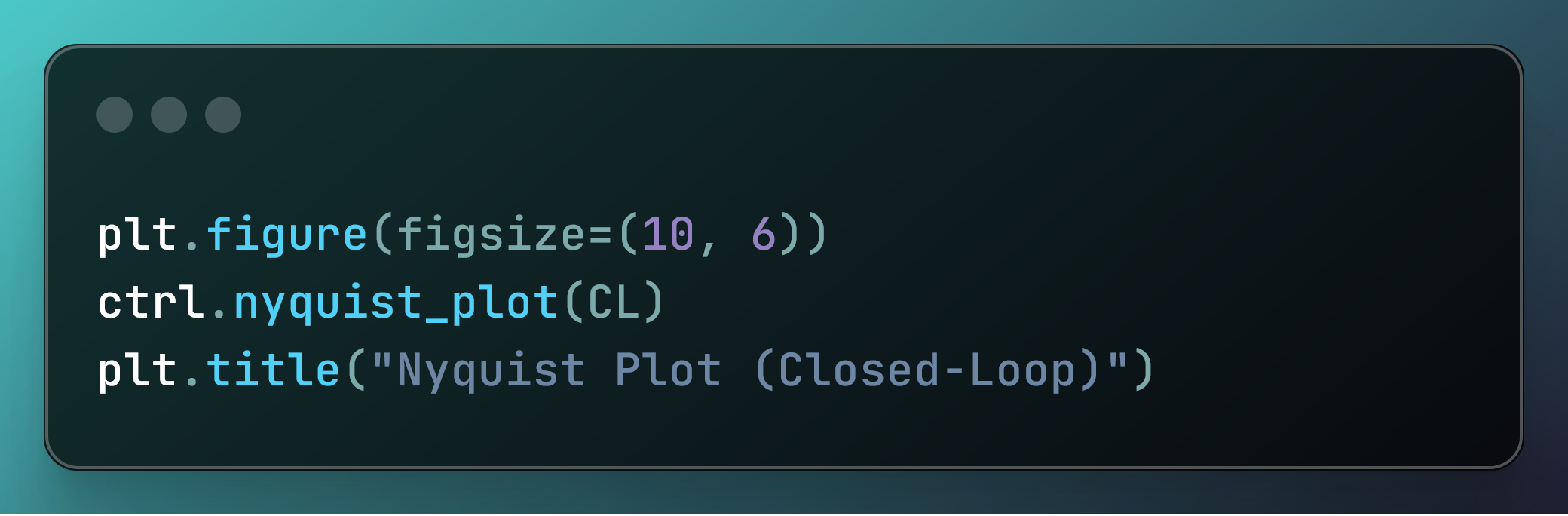

ما این طرح را ایجاد می کنیم:

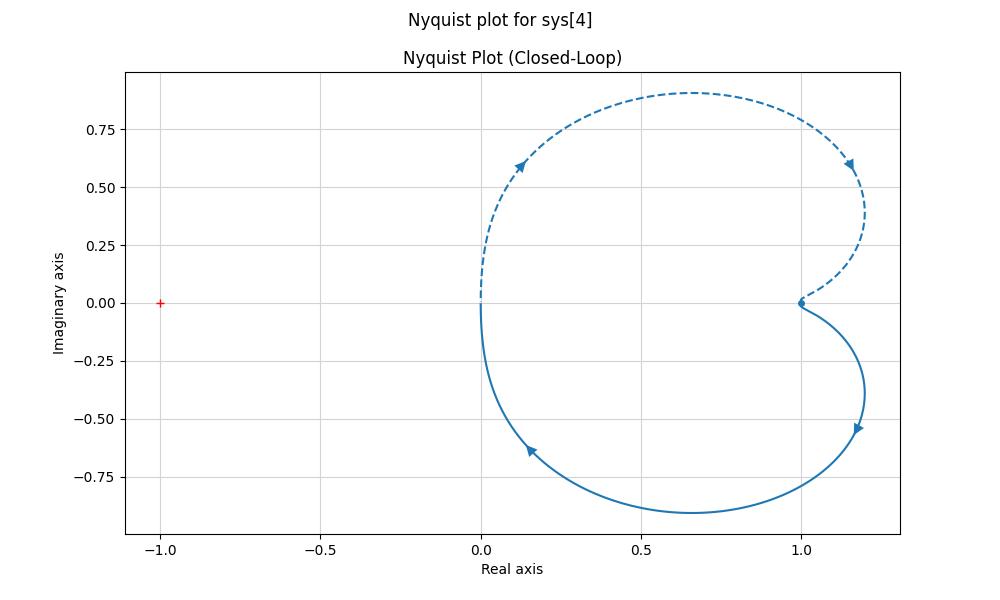
Nyquist Plot ابزاری است که به مهندسان کمک می کند تا به سرعت بررسی کنند که آیا یک سیستم کنترل پایدار است یا نه.

خیلی ساده است:

• اگر در نقطه (1-0) دایره ای در اطراف صلیب سرخ وجود نداشته باشد، سیستم پایدار است.
• اگر دایره هایی در اطراف صلیب قرمز، یعنی دایره هایی در جهت عقربه های ساعت، در نقطه (-1 0) وجود داشته باشد، سیستم ناپایدار است.

از آنجایی که دایره ای در اطراف صلیب سرخ وجود ندارد، این سیستم کنترل پایدار است.

آخرین مرحله پس از طراحی سیستم کنترل موشک

پس از تکمیل طراحی این سیستم کنترل PID، می توانیم از ابزارهایی مانند Simulink برای یافتن مقادیر لازم برای بسیاری از اجزا استفاده کنیم.

به عبارت دیگر، پس از دریافت بهترین متغیرهای کنترل کننده PID، نوبت به یافتن مقادیر اجزای فیزیکی موشک می رسد.

برخی از این مقادیر عبارتند از:

• مقادیر مقاومت برای کنترل جریان جریان
• مقادیر خازن برای ذخیره انرژی
• مقادیر سلف برای مدیریت تداخل الکترومغناطیسی
• مقادیر کالیبراسیون سنسور برای اندازه گیری دقیق داده ها و بازخورد
• استحکام و دوام مواد برای بدنه و باله های موشک
• گشتاور و سرعت مورد نیاز برای موتورهای سروو
• ثابت های فنری برای سیستم های جذب شوک
• رتبه بندی فشار برای مخازن سوخت و اکسید کننده

با تشکر از Simulink، ما می توانیم تمام این مقادیر مورد نیاز برای طراحی یک موشک با توجه به ماموریت آن را بدست آوریم.

با یک سیستم کنترل پایدار، مبتنی بر روی یک کنترلر PID برای کنترل عملکرد انتقال فیزیکی یک موشک، ما می توانیم تمام مقادیر مورد نیاز برای هر جزء را بدست آوریم.

نتیجه گیری: سیستم های کنترل غیر خطی

روش‌های زیادی برای بهینه‌سازی سیستم کنترل خطی زمان ثابت (LTI) وجود دارد:

1. روش ریشه ریشه: قطب های سیستم را برای کاهش نوسانات تنظیم کنید.
2. تجزیه و تحلیل ترسیم نمودار:حاشیه فاز و پایداری را حفظ کنید.
3. طرح نایکیست: ثبات کلی سیستم را تایید کنید.

با این ابزارها امکان ایجاد یک سیستم کنترل وجود دارد.

با این حال، در این process، استفاده از روش هایی مانند روش Ziegler-Nichols برای یافتن سریعتر بهترین متغیرهای کنترل کننده PID تمرین خوبی است.

در اکتشاف خود با یک سیستم موشکی بسیار ساده کار کردیم.

در زندگی واقعی فقط از ابزارهای غیر خطی استفاده می شود زیرا همه سیستم های موشکی سیستم های غیر خطی هستند.

یک مثال کنترل تطبیقی ​​است که در آن سیستم کنترل خود را در زمان واقعی تنظیم می کند تا شرایط در حال تغییر را مدیریت کند

یکی دیگر از روش لیاپانوف است. در این حالت به جای این سه نمودار برای تحلیل پایداری استفاده می شود.

با این حال، process ساخت این سیستم های کنترل همیشه یکسان است. این مقاله توضیح داد که چگونه این process کار می کند و چگونه آن را در یک سیستم زمان ناپذیر اعمال می شود.

GitHub – tiagomonteiro0715/freecodecamp-my-articles-source-code: این مخزن کدی را که من در مقاله‌های خبری freecodecamo خود استفاده می‌کنم در خود نگه می‌دارد.

این مخزن کدی را که در مقاله‌های خبری freecodecamo خود استفاده می‌کنم، نگه می‌دارد. – tiagomonteiro0715/freecodecamp-my-articles-source-code

tiagomonteiro0715GitHub