کاهش ابعاد در پایتون با Scikit-Learn

معرفی

در یادگیری ماشینی، عملکرد یک مدل فقط تا یک نقطه خاص از ویژگی‌های بیشتری بهره می‌برد. هر چه ویژگی های بیشتری به یک مدل داده شود، ابعاد داده ها بیشتر می شود. با افزایش ابعاد، احتمال بیش از حد برازش بیشتر می شود.

چندین تکنیک وجود دارد که می توان از آنها برای مبارزه استفاده کرد بیش از حد، ولی کاهش ابعاد یکی از موثرترین تکنیک ها است. کاهش ابعاد مهم ترین اجزای فضای ویژگی را انتخاب می کند و آنها را حفظ می کند و سایر اجزا را حذف می کند.

چرا کاهش ابعاد مورد نیاز است؟

چند دلیل وجود دارد که کاهش ابعاد در یادگیری ماشین استفاده می شود: برای مقابله با هزینه محاسباتی، کنترل بیش از حد برازش، و تجسم و کمک به تفسیر مجموعه داده های با ابعاد بالا.

اغلب در یادگیری ماشینی، هر چه ویژگی های بیشتری در مجموعه داده وجود داشته باشد، طبقه بندی کننده بهتر می تواند یاد بگیرد. با این حال، ویژگی های بیشتر به معنای هزینه محاسباتی بالاتر نیز می باشد. نه تنها ابعاد بالا می‌تواند منجر به زمان‌های آموزشی طولانی شود، بلکه ویژگی‌های بیشتر اغلب منجر به تطبیق بیش از حد الگوریتم می‌شود، زیرا تلاش می‌کند مدلی ایجاد کند که تمام ویژگی‌های داده‌ها را توضیح دهد.

از آنجایی که کاهش ابعاد تعداد کلی ویژگی‌ها را کاهش می‌دهد، می‌تواند تقاضاهای محاسباتی مرتبط با آموزش یک مدل را کاهش دهد، اما همچنین با ساده نگه داشتن ویژگی‌هایی که به مدل ارائه می‌شوند، به مبارزه با بیش از حد برازش کمک می‌کند.

کاهش ابعاد را می توان در هر دو مورد نظارت و زمینه های یادگیری بدون نظارت. در مورد یادگیری بدون نظارت، کاهش ابعاد اغلب برای پیش پردازش داده ها با انجام انتخاب ویژگی یا استخراج ویژگی استفاده می شود.

الگوریتم های اولیه مورد استفاده برای کاهش ابعاد برای یادگیری بدون نظارت هستند تجزیه و تحلیل مؤلفه های اصلی (PCA) و تجزیه مقدار منفرد (SVD).

در مورد یادگیری نظارت شده، کاهش ابعاد می تواند برای ساده کردن ویژگی های وارد شده به طبقه بندی کننده یادگیری ماشین استفاده شود. متداول ترین روش های مورد استفاده برای کاهش ابعاد برای مشکلات یادگیری نظارت شده است تحلیل تشخیصی خطی (LDA) و PCA، و می توان از آن برای پیش بینی موارد جدید استفاده کرد.

توجه داشته باشید که موارد استفاده شرح داده شده در بالا موارد استفاده عمومی هستند و تنها شرایطی نیستند که این تکنیک ها در آن استفاده می شوند. به هر حال، تکنیک های کاهش ابعاد روش های آماری هستند و استفاده از آنها توسط مدل های یادگیری ماشین محدود نمی شود.

بیایید کمی وقت بگذاریم تا ایده های پشت هر یک از رایج ترین تکنیک های کاهش ابعاد را توضیح دهیم.

تجزیه و تحلیل مؤلفه های اصلی

تجزیه و تحلیل مؤلفه اصلی (PCA) یک روش آماری است که با تجزیه و تحلیل ویژگی های مجموعه داده، ویژگی ها یا ویژگی های جدید داده ها را ایجاد می کند. اساساً ویژگی های داده ها خلاصه یا با هم ترکیب می شوند. همچنین می‌توانید تحلیل مؤلفه‌های اصلی را به‌عنوان «فشار دادن» داده‌ها به چند بعد از فضای ابعاد بسیار بالاتر تصور کنید.

به طور دقیق تر، یک نوشیدنی ممکن است با ویژگی های زیادی توصیف شود، اما بسیاری از این ویژگی ها برای شناسایی نوشیدنی مورد نظر اضافی و نسبتاً بی فایده خواهند بود. به جای توصیف شراب با ویژگی هایی مانند هوادهی، سطوح C02 و غیره، آنها را می توان به راحتی با رنگ، طعم و سن توصیف کرد.

تجزیه و تحلیل مؤلفه اصلی «اصلی» یا تأثیرگذارترین ویژگی های مجموعه داده را انتخاب می کند و ویژگی های مبتنی بر ایجاد می کند. روی آنها را تنها با انتخاب ویژگی هایی که بیشترین تأثیر را دارند روی مجموعه داده، ابعاد کاهش می یابد.

PCA هنگام ایجاد ویژگی های جدید، همبستگی بین متغیرها را حفظ می کند. اجزای اصلی ایجاد شده توسط این تکنیک ترکیب خطی متغیرهای اصلی هستند که با مفاهیمی به نام محاسبه می شوند. بردارهای ویژه.

فرض بر این است که اجزای جدید متعامد هستند یا با یکدیگر ارتباط ندارند.

مثال پیاده سازی PCA

بیایید نگاهی به روش پیاده سازی PCA در آن بیندازیم Scikit-Learn. ما از مجموعه داده طبقه بندی قارچ برای این.

اول، ما نیاز داریم import تمام ماژول های مورد نیاز ما، که شامل PCA می شود، train_test_splitو ابزارهای برچسب گذاری و مقیاس بندی:

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder, StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings("ignore")

پس از بارگذاری داده ها، مقادیر تهی را بررسی می کنیم. ما همچنین داده ها را با رمزگذاری می کنیم LabelEncoder. ویژگی کلاس اولین ستون مجموعه داده است، بنابراین ما ویژگی ها و برچسب ها را بر این اساس تقسیم می کنیم:

m_data = pd.read_csv('mushrooms.csv')




encoder = LabelEncoder()


for col in m_data.columns:
    m_data(col) = encoder.fit_transform(m_data(col))

X_features = m_data.iloc(:,1:23)
y_label = m_data.iloc(:, 0)

اکنون ویژگی‌ها را با مقیاس‌کننده استاندارد مقیاس‌بندی می‌کنیم. این اختیاری است زیرا ما در واقع طبقه‌بندی‌کننده را اجرا نمی‌کنیم، اما ممکن است بر روش تجزیه و تحلیل داده‌های ما توسط PCA تأثیر بگذارد:

scaler = StandardScaler()
X_features = scaler.fit_transform(X_features)

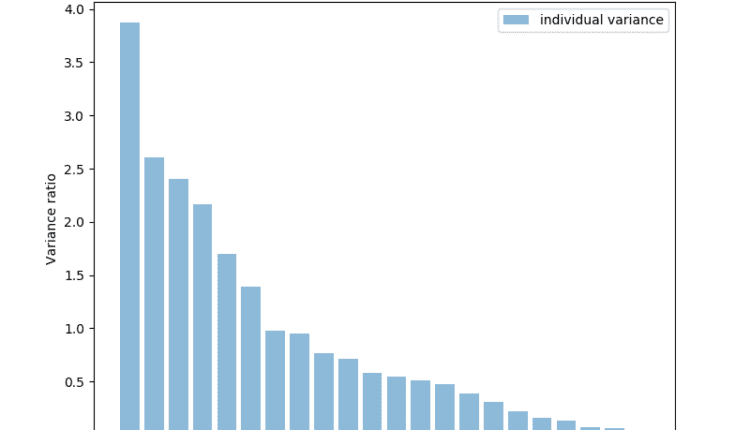
اکنون از PCA برای دریافت لیستی از ویژگی‌ها استفاده می‌کنیم و مشخص می‌کنیم که کدام ویژگی دارای بیشترین قدرت توضیحی یا بیشترین واریانس است. اینها اجزای اصلی هستند. به نظر می رسد که حدود 17 یا 18 ویژگی اکثریت، تقریباً 95 درصد از داده های ما را توضیح می دهند:

pca = PCA()
pca.fit_transform(X_features)
pca_variance = pca.explained_variance_

plt.figure(figsize=(8, 6))
plt.bar(range(22), pca_variance, alpha=0.5, align='center', label='individual variance')
plt.legend()
plt.ylabel('Variance ratio')
plt.xlabel('Principal components')
plt.show()

بیایید ویژگی ها را به 17 ویژگی برتر تبدیل کنیم. سپس یک نمودار پراکنده از طبقه بندی نقطه داده بر اساس رسم می کنیم روی این 17 ویژگی:

pca2 = PCA(n_components=17)
pca2.fit(X_features)
x_3d = pca2.transform(X_features)

plt.figure(figsize=(8,6))
plt.scatter(x_3d(:,0), x_3d(:,5), c=m_data('class'))
plt.show()

بیایید این کار را برای 2 ویژگی برتر نیز انجام دهیم و ببینیم که چگونه طبقه بندی تغییر می کند:

pca3 = PCA(n_components=2)
pca3.fit(X_features)
x_3d = pca3.transform(X_features)

plt.figure(figsize=(8,6))
plt.scatter(x_3d(:,0), x_3d(:,1), c=m_data('class'))
plt.show()

تجزیه مقدار منفرد

هدف از تجزیه ارزش منفرد ساده کردن یک ماتریس و انجام محاسبات با ماتریس است. ماتریس به اجزای تشکیل دهنده آن کاهش می یابد، مشابه هدف PCA. درک نکات و نکات SVD برای پیاده سازی آن در مدل های یادگیری ماشین شما کاملاً ضروری نیست، اما داشتن شهودی برای روش عملکرد آن به شما ایده بهتری درباره زمان استفاده از آن می دهد.

SVD قابل انجام است روی ماتریس‌های پیچیده یا با ارزش واقعی، اما برای سهولت درک این توضیح، به روش تجزیه یک ماتریس با ارزش واقعی می‌پردازیم.

هنگام انجام SVD ما یک ماتریس پر از داده داریم و می خواهیم تعداد ستون های ماتریس را کاهش دهیم. این امر ابعاد ماتریس را کاهش می دهد و در عین حال تا آنجا که ممکن است تغییرپذیری در داده ها حفظ می شود.

می توان گفت که ماتریس A برابر است با جابجایی ماتریس V:

$$
A = U * D * V^t
$$

با فرض اینکه مقداری ماتریس A داریم، می‌توانیم آن ماتریس را به عنوان سه ماتریس دیگر که نامیده می‌شوند نمایش دهیم U، V، و D. ماتریس آ اورجینال را دارد x*y عناصر، در حالی که ماتریس U یک ماتریس متعامد حاوی x*x عناصر و ماتریس V یک ماتریس متعامد متفاوت حاوی y*y عناصر. سرانجام، D یک ماتریس مورب حاوی x*y عناصر.

تجزیه مقادیر برای یک ماتریس شامل تبدیل مقادیر منفرد در ماتریس اصلی به مقادیر مورب ماتریس جدید است. اگر ماتریس های متعامد در اعداد دیگر ضرب شوند، ویژگی های آنها تغییر نمی کند و می توانیم از این ویژگی برای بدست آوردن تقریبی از ماتریس استفاده کنیم. آ. هنگام ضرب ماتریس متعامد با هم ترکیب زمانی که جابجایی ماتریس V، ماتریسی به دست می آوریم که معادل ماتریس اصلی است آ.

وقتی ماتریس را می شکنیم/تجزیه می کنیم آ پایین به U، D، و V، سپس سه ماتریس مختلف داریم که حاوی اطلاعات Matrix هستند آ.

به نظر می رسد که ستون های سمت چپ ماتریس ها اکثر داده های ما را در خود جای می دهند و ما می توانیم فقط همین چند ستون را انتخاب کنیم تا تقریب خوبی از ماتریس داشته باشیم. آ. کار با این ماتریس جدید بسیار ساده تر و راحت تر است، زیرا ابعاد بسیار کمتری دارد.

مثال پیاده سازی SVD

یکی از رایج ترین روش هایی که از SVD استفاده می شود، فشرده سازی تصاویر است. از این گذشته، مقادیر پیکسلی که کانال‌های قرمز، سبز و آبی را در تصویر تشکیل می‌دهند را می‌توان کاهش داد و نتیجه تصویری خواهد بود که پیچیدگی کمتری دارد اما همچنان محتوای تصویر مشابهی دارد. بیایید سعی کنیم از SVD برای فشرده سازی یک تصویر و رندر کردن آن استفاده کنیم.

ما از چندین تابع برای مدیریت فشرده سازی تصویر استفاده خواهیم کرد. ما واقعا فقط نیاز داریم ناپخته و Image تابع از کتابخانه PIL برای انجام این کار، از آنجایی که Numpy روشی برای انجام محاسبه SVD دارد:

import numpy
from PIL import Image

ابتدا، ما فقط یک تابع برای بارگذاری در تصویر می نویسیم و آن را به یک آرایه Numpy تبدیل می کنیم. سپس می خواهیم کانال های رنگ قرمز، سبز و آبی را از تصویر انتخاب کنیم:

def load_image(image):
    image = Image.open(image)
    im_array = numpy.array(image)

    red = im_array(:, :, 0)
    green = im_array(:, :, 1)
    blue = im_array(:, :, 2)

    return red, green, blue

حالا که رنگ ها را داریم، باید کانال های رنگ را فشرده کنیم. می توانیم با فراخوانی تابع SVD Numpy شروع کنیم روی کانال رنگی که می خواهیم سپس آرایه ای از صفرها را ایجاد می کنیم که پس از تکمیل ضرب ماتریس آن را پر می کنیم. سپس محدودیت مقدار واحدی را که می‌خواهیم هنگام انجام محاسبات استفاده کنیم، مشخص می‌کنیم:

def channel_compress(color_channel, singular_value_limit):
    u, s, v = numpy.linalg.svd(color_channel)
    compressed = numpy.zeros((color_channel.shape(0), color_channel.shape(1)))
    n = singular_value_limit

    left_matrix = numpy.matmul(u(:, 0:n), numpy.diag(s)(0:n, 0:n))
    inner_compressed = numpy.matmul(left_matrix, v(0:n, :))
    compressed = inner_compressed.astype('uint8')
    return compressed

red, green, blue = load_image("dog3.jpg")
singular_val_lim = 350

بعد از این کار ضرب ماتریس را انجام می دهیم روی حد مورب و مقدار در ماتریس U، همانطور که در بالا توضیح داده شد. این ماتریس سمت چپ را به دست می آورد و سپس آن را با ماتریس V ضرب می کنیم. این باید مقادیر فشرده‌شده‌ای را که به نوع ‘uint8’ تبدیل می‌کنیم، دریافت کند:

def compress_image(red, green, blue, singular_val_lim):
    compressed_red = channel_compress(red, singular_val_lim)
    compressed_green = channel_compress(green, singular_val_lim)
    compressed_blue = channel_compress(blue, singular_val_lim)

    im_red = Image.fromarray(compressed_red)
    im_blue = Image.fromarray(compressed_blue)
    im_green = Image.fromarray(compressed_green)

    new_image = Image.merge("RGB", (im_red, im_green, im_blue))
    new_image.show()
    new_image.save("dog3-edited.jpg")

compress_image(red, green, blue, singular_val_lim)

ما از این تصویر یک سگ برای آزمایش فشرده سازی SVD خود استفاده خواهیم کرد روی:

ما همچنین نیاز داریم که محدودیت مقدار تکی را که استفاده خواهیم کرد، تنظیم کنیم، فعلاً با 600 شروع می کنیم:

red, green, blue = load_image("dog.jpg")
singular_val_lim = 350

در نهایت، می‌توانیم مقادیر فشرده‌شده را برای سه کانال رنگی دریافت کنیم و با استفاده از PIL، آنها را از آرایه‌های Numpy به اجزای تصویر تبدیل کنیم. سپس فقط باید سه کانال را به هم متصل کنیم و تصویر را نشان دهیم. این تصویر باید کمی کوچکتر و ساده تر از تصویر اصلی باشد:

در واقع، اگر اندازه تصاویر را بررسی کنید، متوجه می‌شوید که تصویر فشرده‌شده کوچک‌تر است، هرچند که ما نیز فشرده‌سازی با اتلاف کمی داشته‌ایم. همچنین می توانید مقداری نویز را در تصویر مشاهده کنید.

شما می توانید با تنظیم محدودیت مقدار منفرد بازی کنید. هرچه حد انتخاب شده کمتر باشد، فشرده سازی بیشتر می شود، اما در یک نقطه خاص، تصویر مصنوع ظاهر می شود و کیفیت تصویر کاهش می یابد:

def compress_image(red, green, blue, singular_val_lim):
    compressed_red = channel_compress(red, singular_val_lim)
    compressed_green = channel_compress(green, singular_val_lim)
    compressed_blue = channel_compress(blue, singular_val_lim)

    im_red = Image.fromarray(compressed_red)
    im_blue = Image.fromarray(compressed_blue)
    im_green = Image.fromarray(compressed_green)

    new_image = Image.merge("RGB", (im_red, im_green, im_blue))
    new_image.show()

compress_image(red, green, blue, singular_val_lim)

تحلیل تشخیصی خطی

تجزیه و تحلیل تشخیص خطی با نمایش داده ها از یک نمودار چند بعدی بر روی یک نمودار خطی عمل می کند. ساده ترین راه برای درک این موضوع با نموداری است که با نقاط داده دو کلاس مختلف پر شده است. با فرض اینکه هیچ خطی وجود ندارد که داده ها را به دو دسته تقسیم کند، نمودار دو بعدی را می توان به یک نمودار 1 بعدی کاهش داد. سپس می توان از این نمودار 1 بعدی برای دستیابی به بهترین جداسازی ممکن از نقاط داده استفاده کرد.

هنگامی که LDA انجام می شود دو هدف اصلی وجود دارد: به حداقل رساندن واریانس دو کلاس و به حداکثر رساندن فاصله بین میانگین دو کلاس داده.

برای دستیابی به این هدف، یک محور جدید در نمودار دو بعدی ترسیم می شود. این محور جدید باید دو نقطه داده را بر اساس جدا کند روی معیارهای ذکر شده قبلی هنگامی که محور جدید ایجاد شد، نقاط داده در نمودار دوبعدی در امتداد محور جدید دوباره ترسیم می شوند.

LDA سه مرحله مختلف را برای انتقال نمودار اصلی به محور جدید انجام می دهد. ابتدا، تفکیک پذیری بین کلاس ها باید محاسبه شود، و این مبتنی است روی فاصله بین میانگین کلاس یا واریانس بین کلاس. در مرحله بعد، واریانس درون کلاسی باید محاسبه شود که فاصله بین میانگین و نمونه برای کلاس های مختلف است. در نهایت، فضای ابعاد پایین‌تری که واریانس بین کلاس‌ها را به حداکثر می‌رساند باید ساخته شود.

LDA زمانی بهترین عملکرد را دارد که وسایل کلاس ها از یکدیگر دور باشند. اگر میانگین توزیع مشترک باشد، LDA نمی‌تواند کلاس‌ها را با یک محور خطی جدید جدا کند.

مثال پیاده سازی LDA

در نهایت، بیایید ببینیم که چگونه می توان از LDA برای کاهش ابعاد استفاده کرد. توجه داشته باشید که LDA می تواند به عنوان یک الگوریتم طبقه بندی علاوه بر کاهش ابعاد استفاده شود.

ما از تایتانیک مجموعه داده برای مثال زیر

بیایید با انجام تمام واردات ضروری خود شروع کنیم:

import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score, f1_score
from sklearn.preprocessing import LabelEncoder, StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

اکنون داده های آموزشی خود را بارگذاری می کنیم، که آنها را به مجموعه های آموزشی و اعتبار سنجی تقسیم می کنیم.

اگرچه، ابتدا باید کمی پیش پردازش داده ها را انجام دهیم. بیایید رها کنیم Name، Cabin، و Ticket ستون‌ها چون اطلاعات مفید زیادی ندارند. همچنین باید داده‌های گمشده را پر کنیم، که در مورد the آن را با مقادیر میانه جایگزین می‌کنیم Age ویژگی و یک S در مورد Embarked ویژگی:

training_data = pd.read_csv("train.csv")


training_data.drop(labels=('Cabin', 'Ticket'), axis=1, inplace=True)

training_data("Age").fillna(training_data("Age").median(), inplace=True)
training_data("Embarked").fillna("S", inplace=True)

همچنین باید ویژگی های غیر عددی را رمزگذاری کنیم. ما هر دو را رمزگذاری خواهیم کرد Sex و Embarked ستون ها. بیایید رها کنیم Name ستون همچنین، زیرا بعید به نظر می رسد که در طبقه بندی مفید باشد:

encoder_1 = LabelEncoder()


encoder_1.fit(training_data("Sex"))


training_sex_encoded = encoder_1.transform(training_data("Sex"))
training_data("Sex") = training_sex_encoded

encoder_2 = LabelEncoder()
encoder_2.fit(training_data("Embarked"))

training_embarked_encoded = encoder_2.transform(training_data("Embarked"))
training_data("Embarked") = training_embarked_encoded


training_data.drop("Name", axis=1, inplace=True)

ما باید مقادیر را مقیاس کنیم، اما Scaler ابزار آرایه‌ها را می‌گیرد، بنابراین مقادیری که می‌خواهیم تغییر شکل دهیم باید ابتدا به آرایه تبدیل شوند. پس از آن، می توانیم داده ها را مقیاس بندی کنیم:

ages_train = np.array(training_data("Age")).reshape(-1, 1)
fares_train = np.array(training_data("Fare")).reshape(-1, 1)

scaler = StandardScaler()

training_data("Age") = scaler.fit_transform(ages_train)
training_data("Fare") = scaler.fit_transform(fares_train)


features = training_data.drop(labels=('PassengerId', 'Survived'), axis=1)
labels = training_data('Survived')

اکنون می توانیم ویژگی ها و برچسب های آموزشی را انتخاب کرده و استفاده کنیم train_test_split برای ایجاد داده های آموزشی و اعتبار سنجی ما. انجام طبقه بندی با LDA آسان است، شما آن را درست مانند هر طبقه بندی کننده دیگری در Scikit-Learn مدیریت می کنید.

فقط متناسب با عملکرد روی داده های آموزشی و آن را پیش بینی کنید روی داده های اعتبار سنجی/آزمایش آن وقت می توانیم print معیارهای پیش بینی در برابر مقادیر واقعی:

X_train, X_val, y_train, y_val = train_test_split(features, labels, test_size=0.2, random_state=27)

model = LDA()
model.fit(X_train, y_train)
preds = model.predict(X_val)
acc = accuracy_score(y_val, preds)
f1 = f1_score(y_val, preds)

print("Accuracy: {}".format(acc))
print("F1 Score: {}".format(f1))

اینجاست print بیرون:

Accuracy: 0.8100558659217877
F1 Score: 0.734375

وقتی نوبت به تبدیل داده ها و کاهش ابعاد می رسد، بیایید یک طبقه بندی رگرسیون لجستیک را اجرا کنیم. روی ابتدا داده ها را به دست آوریم تا بتوانیم عملکردمان را قبل از کاهش ابعاد ببینیم:

logreg_clf = LogisticRegression()
logreg_clf.fit(X_train, y_train)
preds = logreg_clf.predict(X_val)
acc = accuracy_score(y_val, preds)
f1 = f1_score(y_val, preds)

print("Accuracy: {}".format(acc))
print("F1 Score: {}".format(f1))

در اینجا نتایج:

Accuracy: 0.8100558659217877
F1 Score: 0.734375

اکنون ویژگی های داده را با تعیین تعدادی مولفه مورد نظر برای LDA و برازش مدل تغییر می دهیم روی ویژگی ها و برچسب ها سپس فقط ویژگی ها را تبدیل کرده و آن را به یک متغیر جدید ذخیره می کنیم. اجازه دهید print تعداد ویژگی های اصلی و کاهش یافته را حذف کنید:

LDA_transform = LDA(n_components=1)
LDA_transform.fit(features, labels)
features_new = LDA_transform.transform(features)


print('Original feature #:', features.shape(1))
print('Reduced feature #:', features_new.shape(1))


print(LDA_transform.explained_variance_ratio_)

اینجاست print برای کد بالا:

Original feature #: 7
Reduced feature #: 1
(1.)

اکنون فقط باید دوباره با ویژگی‌های جدید تقسیم‌بندی train/test انجام دهیم و دوباره طبقه‌بندی کننده را اجرا کنیم تا ببینیم عملکرد چگونه تغییر کرده است:

X_train, X_val, y_train, y_val = train_test_split(features_new, labels, test_size=0.2, random_state=27)

logreg_clf = LogisticRegression()
logreg_clf.fit(X_train, y_train)
preds = logreg_clf.predict(X_val)
acc = accuracy_score(y_val, preds)
f1 = f1_score(y_val, preds)

print("Accuracy: {}".format(acc))
print("F1 Score: {}".format(f1))

Accuracy: 0.8212290502793296
F1 Score: 0.7500000000000001

نتیجه

ما روش‌های اصلی تکنیک‌های کاهش ابعاد را بررسی کرده‌ایم: تجزیه و تحلیل مؤلفه‌های اصلی، تجزیه ارزش منفرد، و تجزیه و تحلیل متمایز خطی. اینها تکنیک‌های آماری هستند که می‌توانید از آنها برای کمک به مدل‌های یادگیری ماشینی خود برای عملکرد بهتر، مبارزه با بیش از حد مناسب و کمک به تجزیه و تحلیل داده‌ها استفاده کنید.

در حالی که این سه تکنیک رایج ترین تکنیک های کاهش ابعاد هستند، روش های دیگری نیز وجود دارند. سایر تکنیک های ابعادی عبارتند از تقریب هسته و ایزومپ تعبیه طیفی