کوواریانس و همبستگی در پایتون

معرفی

کار با متغیرها در تجزیه و تحلیل داده ها همیشه این سوال را ایجاد می کند: چگونه متغیرها به یکدیگر وابسته، مرتبط و متفاوت هستند؟ اقدامات کوواریانس و همبستگی به ایجاد این کمک می کند.

کوواریانس باعث می شود تغییر در میان متغیرها ما از کوواریانس برای اندازه گیری میزان تغییر دو متغیر با یکدیگر استفاده می کنیم. همبستگی نشان می دهد رابطه بین متغیرها ما از همبستگی برای تعیین اینکه دو متغیر چقدر به یکدیگر مرتبط هستند استفاده می کنیم.

در این مقاله روش محاسبه کوواریانس و همبستگی در پایتون را یاد خواهیم گرفت.

کوواریانس و همبستگی – به عبارت ساده

هر دو کوواریانس و همبستگی در مورد رابطه بین متغیرها هستند. کوواریانس را تعریف می کند انجمن جهت دار بین متغیرها مقادیر کوواریانس از -inf به +inf که در آن مقدار مثبت بیانگر این است که هر دو متغیر در یک جهت حرکت می کنند و مقدار منفی نشان می دهد که هر دو متغیر در جهت مخالف حرکت می کنند.

همبستگی یک معیار آماری استاندارد شده است که میزان ارتباط خطی دو متغیر را بیان می کند (به این معنی که چقدر با هم با نرخ ثابت تغییر می کنند). را قدرت و ارتباط جهت دار رابطه بین دو متغیر با همبستگی تعریف می شود و از 1- تا 1+ متغیر است. مشابه کوواریانس، یک مقدار مثبت نشان می دهد که هر دو متغیر در یک جهت حرکت می کنند در حالی که یک مقدار منفی به ما می گوید که آنها در جهت مخالف حرکت می کنند.

هر دو کوواریانس و همبستگی ابزارهای حیاتی هستند که در کاوش داده ها برای انتخاب ویژگی و تحلیل های چند متغیره استفاده می شوند. به عنوان مثال، سرمایه‌گذاری که به دنبال گسترش ریسک پرتفوی است، ممکن است به دنبال سهامی با کوواریانس بالا باشد، زیرا نشان می‌دهد که قیمت‌های آنها در همان زمان افزایش می‌یابد. با این حال، حرکت مشابه کافی نیست روی خودش سپس سرمایه گذار از متریک همبستگی برای تعیین اینکه چقدر این قیمت های سهام به یکدیگر مرتبط هستند استفاده می کند.

راه اندازی کد پایتون – بازیابی داده های نمونه

با اصولی که از بخش قبل آموختیم، بیایید برای محاسبه کوواریانس در پیش برویم python. برای این مثال، ما کار خواهیم کرد روی معروف مجموعه داده عنبیه. ما فقط با setosa برای خاص بودن گونه ها، از این رو این فقط نمونه ای از مجموعه داده در مورد برخی خواهد بود گل های بنفش دوست داشتنی!

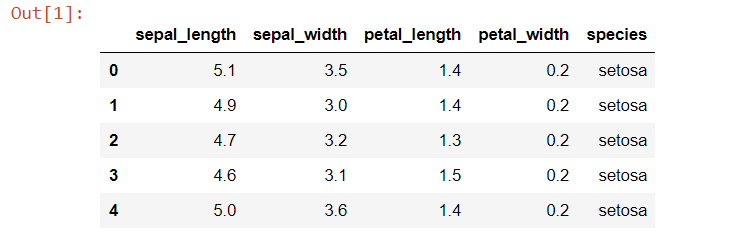
بیایید نگاهی به مجموعه داده بیندازیم، روی که ما آنالیز را انجام خواهیم داد:

ما در حال انتخاب دو ستون برای تجزیه و تحلیل خود هستیم – sepal_length و sepal_width.

در یک فایل پایتون جدید (می توانید آن را نام ببرید covariance_correlation.pyبیایید با ایجاد دو لیست با مقادیر برای شروع کنیم sepal_length و sepal_width خواص گل:

with open('iris_setosa.csv','r') as f:
    g=f.readlines()
    
    sep_length = (float(x.split(',')(0)) for x in g(1:))
    sep_width  = (float(x.split(',')(1)) for x in g(1:))

در علم داده، همیشه به تجسم داده هایی که در حال کار هستید کمک می کند روی. در اینجا یک نمودار رگرسیون Seaborn (نقشه پراکندگی + تناسب رگرسیون خطی) از این ویژگی‌های ستوزا آمده است. روی محورهای مختلف:

از نظر بصری به نظر می رسد که نقاط داده دارای همبستگی بالایی نزدیک به خط رگرسیون هستند. بیایید ببینیم آیا مشاهدات ما با مقادیر کوواریانس و همبستگی آنها مطابقت دارد یا خیر.

محاسبه کوواریانس در پایتون

فرمول زیر کوواریانس را محاسبه می کند:

در فرمول فوق،

• ایکس_من، y_من – عناصر منفرد سری x و y هستند
• x̄، y̅ – میانگین های ریاضی سری x و y هستند
• N – تعداد عناصر مجموعه است

مخرج است N برای کل مجموعه داده و N - 1 در مورد نمونه از آنجایی که مجموعه داده ما نمونه کوچکی از کل مجموعه داده Iris است، از آن استفاده می کنیم N - 1.

با فرمول ریاضی ذکر شده در بالا به عنوان مرجع ما، اجازه دهید این تابع را در پایتون خالص ایجاد کنیم:

def covariance(x, y):
    
    mean_x = sum(x)/float(len(x))
    mean_y = sum(y)/float(len(y))
    
    sub_x = (i - mean_x for i in x)
    sub_y = (i - mean_y for i in y)
    numerator = sum((sub_x(i)*sub_y(i) for i in range(len(sub_x))))
    denominator = len(x)-1
    cov = numerator/denominator
    return cov

with open('iris_setosa.csv', 'r') as f:
    ...
    cov_func = covariance(sep_length, sep_width)
    print("Covariance from the custom function:", cov_func)

ابتدا مقادیر میانگین مجموعه داده های خود را پیدا می کنیم. سپس از درک لیست استفاده می کنیم تا روی هر عنصر در دو سری داده خود تکرار کنیم و مقادیر آنها را از میانگین کم کنیم. آ for اگر ترجیح می دهید از حلقه نیز استفاده شود.

سپس از آن مقادیر میانی دو سری استفاده می کنیم و آنها را با یکدیگر در درک لیست دیگری ضرب می کنیم. ما نتیجه آن لیست را جمع می کنیم و آن را به عنوان ذخیره می کنیم numerator. را denominator محاسبه بسیار ساده تر است، مطمئن شوید که وقتی کوواریانس داده های نمونه را پیدا می کنید، آن را 1 کاهش دهید!

سپس مقدار را زمانی که numerator بر آن تقسیم می شود denominator، که منجر به کوواریانس می شود.

اجرای اسکریپت ما این خروجی را به ما می دهد:

Covariance from the custom function: 0.09921632653061219

مقدار مثبت بیانگر این است که هر دو متغیر در یک جهت حرکت می کنند.

محاسبه همبستگی در پایتون

پرکاربردترین فرمول برای محاسبه ضریب همبستگی “r” پیرسون است:

در فرمول فوق،

• ایکس_من، y_من – عناصر منفرد سری x و y هستند
• شمارنده با کوواریانس مطابقت دارد
• مخرج ها با انحراف استاندارد فردی x و y مطابقت دارند

به نظر می رسد ما در این سری مقالات درباره همه چیزهایی که برای به دست آوردن همبستگی نیاز داریم بحث کرده ایم!

حالا بیایید همبستگی را محاسبه کنیم:

def correlation(x, y):
    
    mean_x = sum(x)/float(len(x))
    mean_y = sum(y)/float(len(y))
    
    sub_x = (i-mean_x for i in x)
    sub_y = (i-mean_y for i in y)
    
    numerator = sum((sub_x(i)*sub_y(i) for i in range(len(sub_x))))
    
    std_deviation_x = sum((sub_x(i)**2.0 for i in range(len(sub_x))))
    std_deviation_y = sum((sub_y(i)**2.0 for i in range(len(sub_y))))
    
    denominator = (std_deviation_x*std_deviation_y)**0.5 
    cor = numerator/denominator
    return cor

with open('iris_setosa.csv', 'r') as f:
    ...
    cor_func = correlation(sep_length, sep_width)
    print("Correlation from the custom function:", cor_func)

از آنجایی که این مقدار به کوواریانس دو متغیر نیاز دارد، تابع ما تقریباً یک بار دیگر آن مقدار را انجام می دهد. هنگامی که کوواریانس محاسبه شد، سپس انحراف معیار را برای هر متغیر محاسبه می کنیم. از آنجا، همبستگی به سادگی تقسیم کوواریانس با ضرب مجذورهای انحراف معیار است.

با اجرای این کد، خروجی زیر را دریافت می کنیم و تأیید می کنیم که این ویژگی ها دارای یک رابطه مثبت (علامت مقدار، یا +، – یا هیچ کدام در صورت 0) و قوی (مقدار نزدیک به 1) هستند:

Correlation from the custom function: 0.7425466856651597

نتیجه

در این مقاله دو ابزار آماری کوواریانس و همبستگی را به تفصیل یاد گرفتیم. ما یاد گرفته ایم که مقادیر آنها برای داده های ما چه معنایی دارد، چگونه آنها در ریاضیات نشان داده می شوند و چگونه آنها را در پایتون پیاده سازی کنیم. هر دوی این معیارها می توانند در تعیین روابط بین دو متغیر بسیار مفید باشند.