پیاده سازی SVM و Kernel SVM با Scikit-Learn پایتون

معرفی

این راهنما اولین قسمت از سه راهنما در مورد ماشین‌های بردار پشتیبانی (SVM) است. در این مجموعه کار خواهیم کرد روی یک اسکناس جعلی مورد استفاده قرار می گیرد، در مورد SVM ساده، سپس در مورد فراپارامترهای SVM و در نهایت، مفهومی به نام ترفند هسته و انواع دیگر SVM ها را بررسی کنید.

اگر می‌خواهید همه راهنماها را بخوانید یا ببینید کدام یک بیشتر به شما علاقه دارند، جدول موضوعات زیر در هر راهنما آمده است:

1. پیاده سازی SVM و Kernel SVM با Scikit-Learn پایتون

• مورد استفاده: اسکناس را فراموش کنید
• پس زمینه SVM ها
• مدل SVM ساده (خطی).
  • درباره مجموعه داده
  • وارد کردن مجموعه داده
  • کاوش مجموعه داده
• پیاده سازی SVM با Scikit-Learn
  • تقسیم داده ها به مجموعه های قطار/آزمون
  • آموزش مدل
  • پیشگویی
  • ارزیابی مدل
  • تفسیر نتایج

2. آشنایی با فراپارامترهای SVM

• فراپارامتر C
• فراپارامتر گاما

3. پیاده سازی دیگر طعم های SVM با Scikit-Learn پایتون

• ایده کلی SVM ها (یک خلاصه)
• هسته (ترفند) SVM
• پیاده سازی SVM هسته غیر خطی با Scikit-Learn
• واردات کتابخانه ها
  • وارد کردن مجموعه داده
  • تقسیم داده ها به ویژگی های (X) و هدف (y)
  • تقسیم داده ها به مجموعه های قطار/آزمون
  • آموزش الگوریتم
• هسته چند جمله ای
  • پیشگویی
  • ارزیابی الگوریتم
• هسته گاوسی
  • پیش بینی و ارزیابی
• هسته سیگموئید
  • پیش بینی و ارزیابی
• مقایسه عملکردهای غیر خطی هسته

مورد استفاده: اسکناس های جعلی

گاهی اوقات مردم راهی برای جعل اسکناس پیدا می کنند. اگر شخصی به آن یادداشت ها نگاه می کند و اعتبار آنها را تأیید می کند، ممکن است سخت باشد که توسط آنها فریب بخورید.

اما چه اتفاقی می‌افتد وقتی کسی نباشد که به هر نت نگاه کند؟ آیا راهی وجود دارد که به طور خودکار بفهمیم که اسکناس جعلی هستند یا واقعی؟

راه های زیادی برای پاسخ به این سوالات وجود دارد. یک پاسخ این است که از هر یادداشت دریافتی عکس بگیرید، تصویر آن را با تصویر یک یادداشت جعلی مقایسه کنید و سپس آن را به عنوان واقعی یا جعلی طبقه بندی کنید. هنگامی که ممکن است انتظار برای تأیید اعتبار یادداشت خسته کننده یا حیاتی باشد، انجام سریع این مقایسه نیز جالب خواهد بود.

از آنجایی که تصاویر در حال استفاده هستند، می‌توان آن‌ها را فشرده، به مقیاس خاکستری کاهش داد و اندازه‌های آن‌ها را استخراج یا کوانتیزه کرد. به این ترتیب، مقایسه بین اندازه‌گیری‌های تصاویر، به جای پیکسل‌های هر تصویر انجام می‌شود.

تا الان راهی پیدا کردیم process و اسکناس ها را با هم مقایسه کنید، اما چگونه آنها را به واقعی یا جعلی طبقه بندی می کنند؟ ما می توانیم از یادگیری ماشین برای انجام این طبقه بندی استفاده کنیم. یک الگوریتم طبقه بندی وجود دارد به نام ماشین بردار پشتیبانی، عمدتاً با شکل اختصاری آن شناخته می شود: SVM.

پس زمینه SVM ها

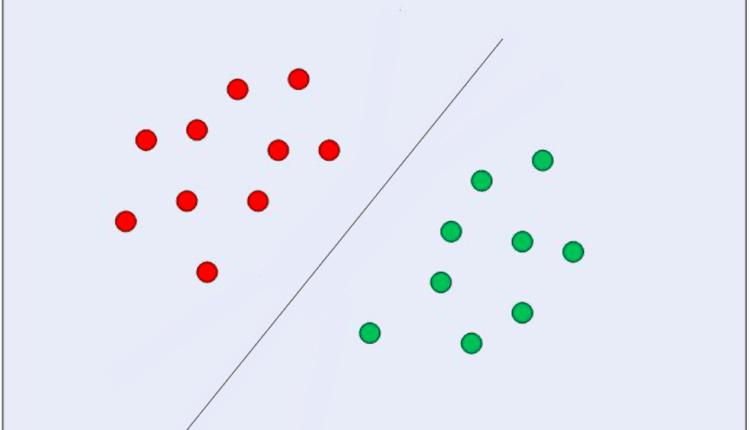
SVM ها ابتدا در سال 1968 توسط ولادمیر واپنیک و الکسی چرووننکیس معرفی شدند. در آن زمان، الگوریتم آنها محدود به طبقه‌بندی داده‌هایی بود که می‌توان تنها با استفاده از یک خط مستقیم از هم جدا شوند، یا داده‌هایی که به صورت خطی قابل تفکیک. ما می توانیم ببینیم که این جدایی چگونه به نظر می رسد:

در تصویر بالا یک خط در وسط داریم که برخی از نقاط آن در سمت چپ و برخی دیگر در سمت راست آن خط قرار دارند. توجه داشته باشید که هر دو گروه از نقاط کاملاً از هم جدا شده اند، هیچ نقطه ای در بین یا حتی نزدیک به خط وجود ندارد. به نظر می رسد بین نقاط مشابه و خطی که آنها را تقسیم می کند یک حاشیه وجود دارد که به آن حاشیه گفته می شود حاشیه جدایی. عملکرد حاشیه جداسازی این است که فضای بین نقاط مشابه و خطی که آنها را تقسیم می کند بزرگتر کند. SVM این کار را با استفاده از چند نقطه انجام می دهد و بردارهای عمود بر آن را برای حمایت از تصمیم برای حاشیه خط محاسبه می کند. آن ها هستند بردارهای پشتیبانی که بخشی از نام الگوریتم هستند. بعداً در مورد آنها بیشتر خواهیم فهمید. و خط مستقیمی که در وسط می بینیم با روش هایی پیدا می شود که به حداکثر رساندن آن فاصله بین خط و نقاط، یا اینکه حاشیه جداسازی را به حداکثر می‌رساند. آن روش ها از حوزه نشات می گیرند نظریه بهینه سازی.

در مثالی که اکنون دیدیم، هر دو گروه از نقاط را می توان به راحتی از هم جدا کرد، زیرا هر نقطه مجزا به نقاط مشابه خود نزدیک است و دو گروه از یکدیگر دور هستند.

اما اگر راهی برای جداسازی داده ها با استفاده از یک خط مستقیم وجود نداشته باشد چه اتفاقی می افتد؟ اگر نقاط نامرتب وجود داشته باشد، یا اگر منحنی مورد نیاز است؟

برای حل این مشکل، SVM بعداً در دهه 1990 اصلاح شد تا بتواند داده هایی را که دارای نقاط دور از تمایل اصلی آن هستند، مانند نقاط پرت، یا مسائل پیچیده تر که بیش از دو بعد دارند و به صورت خطی قابل تفکیک نیستند، طبقه بندی کند. .

نکته جالب این است که تنها در سال های اخیر SVM به طور گسترده مورد استفاده قرار گرفته است، عمدتاً به دلیل توانایی آنها در دستیابی به گاه بیش از 90٪ از پاسخ های صحیح یا دقت، برای مشکلات دشوار

SVM ها در مقایسه با سایر الگوریتم های یادگیری ماشینی، پس از پایه گذاری، به روشی منحصر به فرد پیاده سازی می شوند روی توضیحات آماری از چیستی یادگیری، یا روی تئوری یادگیری آماری.

در این مقاله، الگوریتم‌های Support Vector Machines، نظریه مختصر پشت ماشین بردار پشتیبان و پیاده‌سازی آن‌ها در کتابخانه Scikit-Learn پایتون را خواهیم دید. سپس به سمت مفهوم SVM دیگری که به نام شناخته می شود حرکت خواهیم کرد هسته SVM، یا ترفند هسته، و همچنین آن را با کمک Scikit-Learn پیاده سازی خواهد کرد.

مدل SVM ساده (خطی).

درباره مجموعه داده

به دنبال مثال ارائه شده در مقدمه، از مجموعه داده ای استفاده خواهیم کرد که اندازه گیری تصاویر اسکناس های واقعی و جعلی را دارد.

وقتی به دو نت نگاه می کنیم، چشمان ما معمولاً آنها را از چپ به راست اسکن می کنند و بررسی می کنند که در کجا ممکن است شباهت یا عدم شباهت وجود داشته باشد. ما به دنبال یک نقطه سیاه هستیم که قبل از یک نقطه سبز، یا یک علامت براق که بالای یک تصویر قرار دارد، می‌گردیم. به این معنی که ترتیبی وجود دارد که ما به یادداشت ها نگاه می کنیم. اگر می دانستیم که نقاط سبز و سیاه وجود دارد، اما نه اگر نقطه سبز قبل از سیاه باشد، یا اگر سیاه قبل از سبز باشد، تشخیص بین نت ها سخت تر می شد.

روشی مشابه با آنچه که اکنون توضیح دادیم وجود دارد که می تواند در تصاویر اسکناس اعمال شود. به طور کلی، این روش عبارت است از تبدیل پیکسل های تصویر به یک سیگنال، سپس در نظر گرفتن ترتیبی که هر سیگنال مختلف در تصویر رخ می دهد با تبدیل آن به امواج کوچک، یا موجک ها. پس از به دست آوردن موجک ها، راهی برای دانستن ترتیبی وجود دارد که برخی از سیگنال ها قبل از سیگنال دیگری اتفاق می افتد، یا زمان، اما نه دقیقاً چه سیگنالی. برای دانستن آن، فرکانس های تصویر باید به دست آید. آنها با روشی به دست می آیند که تجزیه هر سیگنال را انجام می دهد، به نام روش فوریه.

هنگامی که بعد زمان از طریق موجک ها و بعد فرکانس از طریق روش فوریه به دست آمد، زمان و فرکانس روی هم قرار می گیرند تا ببینیم چه زمانی هر دو با هم تطابق دارند، این همان پیچیدگی تحلیل و بررسی. کانولوشن تناسبی را به دست می‌آورد که موجک‌ها را با فرکانس‌های تصویر مطابقت می‌دهد و مشخص می‌کند که کدام فرکانس برجسته‌تر است.

این روش که شامل یافتن موجک ها، فرکانس های آنها و سپس برازش هر دوی آنها است، نامیده می شود. تبدیل موجک. تبدیل موجک دارای ضرایب است و از آن ضرایب برای به دست آوردن اندازه گیری هایی که در مجموعه داده داریم استفاده شده است.

وارد کردن مجموعه داده

مجموعه داده یادداشت‌های بانکی که می‌خواهیم در این بخش استفاده کنیم همان است که در بخش طبقه‌بندی آموزش درخت تصمیم استفاده شد.

اجازه دهید import داده ها را به یک پاندا تبدیل می کند dataframe ساختار، و نگاهی به پنج ردیف اول آن با head() روش.

توجه داشته باشید که داده ها در یک ذخیره می شوند txt فرمت فایل (متن) که با کاما از هم جدا شده و بدون هدر است. با خواندن آن به صورت a می توانیم آن را به صورت جدول بازسازی کنیم csv، مشخص کردن separator به عنوان کاما، و اضافه کردن نام ستون با names بحث و جدل.

بیایید این سه مرحله را همزمان دنبال کنیم و سپس به پنج ردیف اول داده ها نگاه کنیم:

import pandas as pd

data_link = "https://archive.ics.uci.edu/ml/machine-learning-databases/00267/data_banknote_authentication.txt"
col_names = ("variance", "skewness", "curtosis", "entropy", "class")

bankdata = pd.read_csv(data_link, names=col_names, sep=",", header=None)
bankdata.head()

این منجر به:

    variance    skewness    curtosis    entropy     class
0   3.62160     8.6661      -2.8073     -0.44699    0
1   4.54590     8.1674      -2.4586     -1.46210    0
2   3.86600     -2.6383     1.9242      0.10645     0
3   3.45660     9.5228      -4.0112     -3.59440    0
4   0.32924     -4.4552     4.5718      -0.98880    0

می بینیم که پنج ستون در مجموعه داده ما وجود دارد، یعنی: variance، skewness، curtosis، entropy، و class. در پنج سطر، چهار ستون اول با اعدادی مانند 3.62160، 8.6661، -2.8073 یا مداوم ارزش ها و آخرین class پنج سطر اول ستون با 0 یا a پر شده است گسسته ارزش.

از آنجایی که هدف ما این است که پیش بینی کنیم آیا یک اسکناس معتبر است یا نه، می توانیم این کار را بر اساس چهار ویژگی اسکناس انجام دهیم:

• variance تصویر تبدیل موجک. به طور کلی، واریانس یک مقدار پیوسته است که میزان نزدیک یا دور بودن نقاط داده به مقدار متوسط ​​داده ها را اندازه می گیرد. اگر نقاط به مقدار متوسط ​​داده ها نزدیکتر باشند، توزیع به توزیع نرمال نزدیکتر است، که معمولاً به این معنی است که مقادیر آن به خوبی توزیع شده و تا حدودی قابل پیش بینی آسان تر است. در زمینه تصویر فعلی، این واریانس ضرایبی است که از تبدیل موجک حاصل می شود. هر چه واریانس کمتر باشد، ضرایب به ترجمه تصویر واقعی نزدیکتر است.

• skewness تصویر تبدیل موجک. چولگی یک مقدار پیوسته است که عدم تقارن یک توزیع را نشان می دهد. اگر مقادیر بیشتری در سمت چپ میانگین وجود داشته باشد، توزیع برابر است دارای انحراف منفی، اگر مقادیر بیشتری در سمت راست میانگین وجود داشته باشد، توزیع است دارای انحراف مثبتو اگر میانگین، حالت و میانه یکسان باشد، توزیع است متقارن. هرچه یک توزیع متقارن تر باشد، به توزیع نرمال نزدیک تر است و همچنین مقادیر آن به خوبی توزیع شده است. در شرایط فعلی، این چولگی ضرایبی است که از تبدیل موجک حاصل می شود. هر چه متقارن تر باشد، ضرایب نزدیک تر استvariance، skewness، curtosis، entropyبرای ترجمه تصویر واقعی.

• curtosis (یا کشیدگی) تصویر تبدیل شده موجک. کشش یک مقدار پیوسته است که مانند چولگی، شکل یک توزیع را نیز توصیف می کند. بسته به روی ضریب کشیدگی (k)، یک توزیع – در مقایسه با توزیع نرمال می تواند کم و بیش مسطح باشد – یا داده های کمتر یا بیشتر در انتهای یا دم آن داشته باشد. هنگامی که توزیع گسترده تر و مسطح تر باشد، نامیده می شود پلاتیکورتیک; وقتی کمتر پخش شده و بیشتر در وسط متمرکز شده است، مزوکورتیک; و هنگامی که توزیع تقریباً به طور کامل در وسط متمرکز شود، نامیده می شود لپتوکورتیک. این همان حالت واریانس و چولگی موارد قبلی است، هر چه توزیع مزوکورتیک تر باشد، ضرایب به ترجمه تصویر واقعی نزدیک تر است.

• entropy از تصویر آنتروپی نیز یک مقدار پیوسته است، معمولاً تصادفی بودن یا بی نظمی را در یک سیستم اندازه گیری می کند. در زمینه یک تصویر، آنتروپی تفاوت بین یک پیکسل و پیکسل های همسایه اش را اندازه گیری می کند. برای زمینه ما، هرچه ضرایب آنتروپی بیشتری داشته باشند، هنگام تغییر شکل تصویر تلفات بیشتری وجود دارد – و هر چه آنتروپی کوچکتر باشد، از دست دادن اطلاعات کمتر است.

متغیر پنجم بود class متغیری که احتمالاً دارای مقادیر 0 و 1 است که می‌گوید آیا نت واقعی یا جعلی بوده است.

ما می توانیم بررسی کنیم که آیا ستون پنجم حاوی صفر و یک با پاندا است یا خیر unique() روش:

bankdata('class').unique()

روش بالا برمی گرداند:

array((0, 1)) 

روش بالا یک آرایه با مقادیر 0 و 1 برمی گرداند. این بدان معنی است که تنها مقادیر موجود در ردیف های کلاس ما صفر و یک است. آماده استفاده به عنوان هدف در یادگیری تحت نظارت ما

• class از تصویر این یک مقدار صحیح است، زمانی که تصویر جعلی است 0 و زمانی که تصویر واقعی است 1 است.

از آنجایی که ما یک ستون با حاشیه نویسی تصاویر واقعی و فراموش شده داریم، به این معنی است که نوع یادگیری ما است تحت نظارت.

ما همچنین می‌توانیم با مشاهده تعداد ردیف‌های داده‌ها از طریق shape ویژگی:

bankdata.shape

این خروجی:

(1372, 5)

خط بالا به این معنی است که 1372 ردیف از تصاویر اسکناس تبدیل شده و 5 ستون وجود دارد. این داده هایی است که ما تجزیه و تحلیل خواهیم کرد.

ما مجموعه داده خود را وارد کرده ایم و چند بررسی انجام داده ایم. اکنون می توانیم داده های خود را برای درک بهتر آن بررسی کنیم.

کاوش مجموعه داده

ما فقط دیدیم که در ستون کلاس فقط صفر و یک وجود دارد، اما همچنین می‌توانیم بدانیم که به چه نسبتی هستند – به عبارت دیگر – اگر صفرها بیشتر از یک، یک‌ها بیشتر از صفر باشد یا اعداد صفرها همان تعداد یک هاست یعنی هستند متعادل.

برای دانستن نسبت می توانیم هر یک از مقادیر صفر و یک داده ها را با آن بشماریم value_counts() روش:

bankdata('class').value_counts()

این خروجی:

0    762
1    610
Name: class, dtype: int64

در نتیجه بالا می بینیم که 762 صفر و 610 یک یا 152 صفر بیشتر از یک وجود دارد. این بدان معنی است که ما کمی بیشتر از تصاویر واقعی جعلی داریم، و اگر این اختلاف بزرگتر بود، به عنوان مثال، 5500 صفر و 610 یک، می تواند بر نتایج ما تأثیر منفی بگذارد. هنگامی که سعی می کنیم از آن نمونه ها در مدل خود استفاده کنیم – هر چه تعداد نمونه ها بیشتر باشد، معمولاً به این معنی است که مدل باید اطلاعات بیشتری بین یادداشت های جعلی یا واقعی تصمیم بگیرد – اگر نمونه های یادداشت واقعی کمی وجود داشته باشد، مدل مستعد این است که هنگام تلاش برای شناسایی آنها اشتباه می کنند.

ما قبلاً می دانیم که 152 یادداشت جعلی دیگر وجود دارد، اما آیا می توانیم مطمئن باشیم که آنها نمونه های کافی برای یادگیری مدل هستند؟ دانستن اینکه چه تعداد مثال برای یادگیری نیاز است یک سوال بسیار سخت برای پاسخگویی است، در عوض، می‌توانیم تلاش کنیم تا بفهمیم که تفاوت بین کلاس‌ها چقدر است.

اولین قدم استفاده از پاندا است value_counts() دوباره روش، اما حالا بیایید درصد را با گنجاندن آرگومان ببینیم normalize=True:

bankdata('class').value_counts(normalize=True)

این normalize=True درصد داده های هر کلاس را محاسبه می کند. تا کنون، درصد جعلی (0) و واقعی (1) عبارت است از:

0    0.555394
1    0.444606
Name: class, dtype: float64

این بدان معنی است که تقریباً (~) 56٪ از مجموعه داده ما جعلی است و 44٪ از آن واقعی است. این نسبت 56٪ -44٪ را به ما می دهد، که همان تفاوت 12٪ است. این از نظر آماری یک تفاوت کوچک در نظر گرفته می شود، زیرا فقط کمی بالاتر از 10٪ است، بنابراین داده ها متعادل در نظر گرفته می شوند. اگر به جای نسبت 56:44، نسبت 80:20 یا 70:30 وجود داشته باشد، داده های ما نامتعادل در نظر گرفته می شوند و ما باید درمان عدم تعادل را انجام دهیم، اما خوشبختانه اینطور نیست.

ما همچنین می توانیم این تفاوت را به صورت بصری، با نگاهی به توزیع کلاس یا هدف با یک هیستوگرام آغشته به پاندا، با استفاده از:

bankdata('class').plot.hist();

این یک هیستوگرام با استفاده از ساختار چارچوب داده به طور مستقیم، در ترکیب با matplotlib کتابخانه ای که در پشت صحنه است.

با نگاه کردن به هیستوگرام، می توانیم مطمئن شویم که مقادیر هدف ما 0 یا 1 است و داده ها متعادل هستند.

این تجزیه و تحلیل ستونی بود که ما سعی داشتیم آن را پیش بینی کنیم، اما در مورد تجزیه و تحلیل ستون های دیگر داده هایمان چطور؟

می‌توانیم نگاهی به اندازه‌گیری‌های آماری داشته باشیم describe() روش چارچوب داده ما نیز می توانیم استفاده کنیم .T transpose – برای معکوس کردن ستون‌ها و ردیف‌ها، که باعث می‌شود مقایسه بین مقادیر مستقیم‌تر شود:

bankdata.describe().T

این منجر به:

            count   mean        std         min         25%         50%         75%         max
variance    1372.0  0.433735    2.842763    -7.0421     -1.773000   0.49618     2.821475    6.8248
skewness    1372.0  1.922353    5.869047    -13.7731    -1.708200   2.31965     6.814625    12.9516
curtosis    1372.0  1.397627    4.310030    -5.2861     -1.574975   0.61663     3.179250    17.9274
entropy     1372.0  -1.191657   2.101013    -8.5482     -2.413450   -0.58665    0.394810    2.4495
class       1372.0  0.444606    0.497103    0.0000       0.000000   0.00000     1.000000    1.0000

توجه داشته باشید که ستون‌های چولگی و کشیدگی مقادیر متوسطی دارند که با مقادیر انحراف استاندارد فاصله دارند، این نشان می‌دهد که مقادیری که از تمایل مرکزی داده‌ها دورتر هستند یا دارای تنوع بیشتری هستند.

ما همچنین می‌توانیم با ترسیم هیستوگرام هر ویژگی در یک حلقه for نگاهی به توزیع هر ویژگی به صورت بصری بیندازیم. علاوه بر بررسی توزیع، جالب است که ببینیم چگونه نقاط هر کلاس در مورد هر ویژگی از هم جدا می شوند. برای انجام این کار، می‌توانیم نمودار پراکنده‌ای را ترسیم کنیم که ترکیبی از ویژگی‌ها را بین آن‌ها ایجاد کرده و رنگ‌های متفاوتی را به هر نقطه با توجه به کلاس آن اختصاص دهیم.

بیایید با توزیع هر یک از ویژگی ها شروع کنیم و هیستوگرام هر ستون داده به جز برای را رسم کنیم class ستون این class ستون با موقعیت خود در آن در نظر گرفته نخواهد شد bankdata آرایه ستون ها همه ستون ها به جز آخرین ستون با انتخاب خواهند شد columns(:-1):

import matplotlib.pyplot as plt

for col in bankdata.columns(:-1):
    plt.title(col)
    bankdata(col).plot.hist() 
    plt.show();

پس از اجرای کد بالا، می توانیم هر دو را مشاهده کنیم skewness و entropy توزیع داده ها دارای انحراف منفی هستند و kurtosis دارای انحراف مثبت است. همه توزیع ها متقارن هستند و variance تنها توزیعی است که نزدیک به نرمال است.

اکنون می توانیم حرکت کنیم روی به قسمت دوم، و نمودار پراکندگی هر متغیر را رسم کنید. برای این کار می‌توانیم تمام ستون‌ها به جز کلاس with را انتخاب کنیم columns(:-1)، از Seaborn’s استفاده کنید scatterplot() و دو حلقه برای به دست آوردن تغییرات در جفت شدن برای هر یک از ویژگی ها. همچنین می‌توانیم جفت شدن یک ویژگی با خودش را حذف کنیم، با آزمایش اینکه آیا اولین ویژگی با ویژگی دوم برابر است یا خیر. if statement.

import seaborn as sns

for feature_1 in bankdata.columns(:-1):
    for feature_2 in bankdata.columns(:-1):
        if feature_1 != feature_2: 
            print(feature_1, feature_2) 
            sns.scatterplot(x=feature_1, y=feature_2, data=bankdata, hue='class') 
            plt.show();

توجه داشته باشید که همه نمودارها دارای نقاط داده واقعی و جعلی هستند که به وضوح از یکدیگر جدا نشده اند، این بدان معنی است که نوعی برهم نهی کلاس ها وجود دارد. از آنجایی که یک مدل SVM از یک خط برای جداسازی بین کلاس ها استفاده می کند، آیا می توان هر یک از آن گروه ها در نمودارها را تنها با استفاده از یک خط جدا کرد؟ بعید به نظر می رسد. این همان چیزی است که بیشتر داده های واقعی به نظر می رسد. نزدیکترین چیزی که می توانیم به جدایی برسیم در ترکیب آنهاست skewness و variance، یا entropy و variance توطئه ها این احتمالا به دلیل variance داده ها دارای شکل توزیع نزدیک تر به نرمال هستند.

اما نگاه کردن به تمام این نمودارها به ترتیب می تواند کمی سخت باشد. ما این گزینه را داریم که با استفاده از همه نمودارهای توزیع و پراکندگی را با هم نگاه کنیم Seaborn‘s pairplot().

هر دو حلقه for قبلی که انجام داده بودیم را می توان با این خط جایگزین کرد:

sns.pairplot(bankdata, hue='class');

با نگاهی به طرح جفت، به نظر می رسد که در واقع، kurtosis و variance ساده ترین ترکیب ویژگی ها خواهد بود، بنابراین کلاس های مختلف را می توان با یک خط یا به صورت خطی قابل تفکیک.

اگر بیشتر داده‌ها از جداسازی خطی دور هستند، می‌توانیم سعی کنیم آن‌ها را با کاهش ابعاد آن پیش پردازش کنیم و همچنین مقادیر آن را عادی کنیم تا توزیع را به حالت عادی نزدیک‌تر کنیم.

برای این مورد، بیایید بدون پیش پردازش بیشتر از داده ها همانطور که هست استفاده کنیم و بعداً می توانیم یک مرحله به عقب برگردیم، به پیش پردازش داده ها اضافه کنیم و نتایج را با هم مقایسه کنیم.

پیاده سازی SVM با Scikit-Learn

قبل از پرداختن به تئوری روش عملکرد SVM، می‌توانیم اولین مدل پایه خود را با داده‌ها و Scikit-Learn بسازیم. دسته بندی بردار پشتیبانی یا SVC کلاس

مدل ما ضرایب موجک را دریافت می کند و سعی می کند آنها را بر اساس طبقه بندی کند روی کلاس. اولین قدم در این process این است که ضرایب یا امکانات از کلاس یا هدف. بعد از آن مرحله، مرحله دوم تقسیم بیشتر داده ها به مجموعه ای است که برای یادگیری مدل استفاده می شود یا مجموعه قطار و دیگری که برای ارزیابی مدل استفاده خواهد شد مجموعه تست.

تقسیم داده ها به مجموعه های قطار/آزمون

در جلسه قبل، داده ها را درک و بررسی کردیم. اکنون، می‌توانیم داده‌های خود را به دو آرایه تقسیم کنیم – یکی برای چهار ویژگی، و دیگری برای پنجمین ویژگی یا ویژگی هدف. از آنجایی که می خواهیم کلاس را بسته به آن پیش بینی کنیم روی ضرایب موجک، ما y خواهد بود class ستون و ما X خواهد شد variance، skewness، curtosis، و entropy ستون ها.

برای تفکیک هدف و ویژگی‌ها، می‌توانیم فقط آن را نسبت دهیم class ستون به y، بعداً آن را از dataframe حذف می کنیم تا ستون های باقی مانده را به آن نسبت دهیم X با .drop() روش:

y = bankdata('class')
X = bankdata.drop('class', axis=1) 

هنگامی که داده‌ها به ویژگی‌ها و برچسب‌ها تقسیم می‌شوند، می‌توانیم آن‌ها را بیشتر به مجموعه‌های قطار و آزمایش تقسیم کنیم. این را می توان با دست انجام داد، اما model_selection کتابخانه Scikit-Learn شامل train_test_split() روشی که به ما امکان می دهد داده ها را به صورت تصادفی به مجموعه های قطار و آزمایش تقسیم کنیم.

برای استفاده از آن، ما می توانیم import کتابخانه، تماس بگیرید train_test_split() روش، عبور کردن X و y داده ها و تعریف الف test_size به عنوان استدلال بگذرد. در این صورت آن را به صورت تعریف می کنیم 0.20– این بدان معناست که 20٪ از داده ها برای آزمایش و 80٪ دیگر برای آموزش استفاده می شود.

این روش به‌طور تصادفی نمونه‌هایی را با توجه به درصدی که تعریف کرده‌ایم، می‌گیرد، اما به جفت‌های Xy احترام می‌گذارد، مبادا نمونه‌برداری کاملاً این رابطه را با هم مخلوط کند.

از زمان نمونه گیری process ذاتاً تصادفی است، در هنگام اجرای روش همیشه نتایج متفاوتی خواهیم داشت. برای اینکه بتوانیم نتایج مشابه یا نتایج قابل تکرار داشته باشیم، می توانیم ثابتی به نام SEED با مقدار 42 تعریف کنیم.

برای این کار می توانید اسکریپت زیر را اجرا کنید:

from sklearn.model_selection import train_test_split

SEED = 42

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = SEED)

توجه داشته باشید که train_test_split() روش قبلاً را برمی گرداند X_train، X_test، y_train، y_test به این ترتیب تنظیم می شود. ما میتوانیم print تعداد نمونه های جدا شده برای قطار و آزمایش با گرفتن اولین (0) عنصر از shape اموال بازگشتی تاپل:

xtrain_samples = X_train.shape(0)
xtest_samples = X_test.shape(0)

print(f'There are {xtrain_samples} samples for training and {xtest_samples} samples for testing.')

این نشان می دهد که 1097 نمونه برای آموزش و 275 نمونه برای تست وجود دارد.

آموزش مدل

ما داده ها را به مجموعه های قطار و تست تقسیم کرده ایم. اکنون زمان ایجاد و آموزش یک مدل SVM است روی داده های قطار برای انجام آن، ما می توانیم import Scikit-Learn’s svm کتابخانه به همراه دسته بندی بردار پشتیبانی کلاس، یا SVC کلاس

پس از وارد کردن کلاس، می‌توانیم یک نمونه از آن ایجاد کنیم – از آنجایی که ما یک مدل SVM ساده ایجاد می‌کنیم، سعی می‌کنیم داده‌هایمان را به صورت خطی جدا کنیم، بنابراین می‌توانیم یک خط برای تقسیم داده‌هایمان ترسیم کنیم – که مانند استفاده از یک تابع خطی – با تعریف kernel='linear' به عنوان یک استدلال برای طبقه بندی کننده:

from sklearn.svm import SVC
svc = SVC(kernel='linear')

به این ترتیب، طبقه بندی کننده سعی می کند یک تابع خطی پیدا کند که داده های ما را از هم جدا می کند. پس از ایجاد مدل، آن را آموزش دهیم، یا مناسب آن را با داده های قطار، با استفاده از fit() روش و دادن به X_train ویژگی ها و y_train اهداف به عنوان استدلال

برای آموزش مدل می توانیم کد زیر را اجرا کنیم:

svc.fit(X_train, y_train)

درست مثل آن مدل آموزش دیده است. تا اینجا ما داده ها را درک کرده ایم، آن ها را تقسیم کرده ایم، یک مدل SVM ساده ایجاد کرده ایم و مدل را با داده های قطار تطبیق داده ایم.

گام بعدی این است که بفهمیم این تناسب چقدر توانسته داده های ما را توصیف کند. به عبارت دیگر، برای پاسخ به اینکه آیا یک SVM خطی انتخاب مناسبی بود یا خیر.

پیشگویی

یک راه برای پاسخ به این که آیا مدل موفق به توصیف داده ها شده است یا خیر، محاسبه و بررسی طبقه بندی است معیارهای.

با توجه به اینکه یادگیری تحت نظارت است، می توانیم با آن پیش بینی کنیم X_test و آن نتایج پیش بینی را مقایسه کنید – که ممکن است آنها را بخوانیم y_pred – با واقعی y_test، یا حقیقت زمین.

برای پیش بینی برخی از داده ها، مدل است predict() روش را می توان به کار گرفت. این روش ویژگی های تست را دریافت می کند، X_test، به عنوان یک آرگومان و یک پیش بینی، 0 یا 1، برای هر یک از آنها برمی گرداند X_testردیف های

پس از پیش بینی X_test داده ها، نتایج در یک ذخیره می شود y_pred متغیر. بنابراین هر یک از کلاس های پیش بینی شده با مدل SVM خطی ساده در حال حاضر در y_pred متغیر.

این کد پیش بینی است:

y_pred = svc.predict(X_test)

با توجه به اینکه پیش‌بینی‌ها را داریم، اکنون می‌توانیم آنها را با نتایج واقعی مقایسه کنیم.

ارزیابی مدل

روش های مختلفی برای مقایسه پیش بینی ها با نتایج واقعی وجود دارد و آنها جنبه های مختلف یک طبقه بندی را اندازه گیری می کنند. برخی از پرکاربردترین معیارهای طبقه بندی عبارتند از:

1. ماتریس سردرگمی: زمانی که باید بدانیم چه مقدار از نمونه ها را درست یا غلط گرفته ایم هر کلاس. مقادیری که درست و به درستی پیش بینی شده بودند نامیده می شوند نکات مثبت واقعیمواردی که مثبت پیش بینی شده بودند اما مثبت نبودند نامیده می شوند مثبت کاذب. همان نامگذاری از منفی های واقعی و منفی های کاذب برای مقادیر منفی استفاده می شود.

2. دقت، درستی: وقتی هدف ما این است که بفهمیم چه مقادیر پیش‌بینی درستی توسط طبقه‌بندی‌کننده ما صحیح در نظر گرفته شده است. دقت آن مقادیر مثبت واقعی را بر نمونه هایی که به عنوان مثبت پیش بینی شده بودند تقسیم می کند.

$$
دقت = \frac{\text{موارد مثبت واقعی}}{\text{موارد مثبت واقعی} + \text{مورد مثبت نادرست}}
$$

3. به خاطر آوردن: معمولاً همراه با دقت محاسبه می شود تا بفهمیم چه تعداد از مثبت های واقعی توسط طبقه بندی کننده ما شناسایی شده اند. فراخوان با تقسیم مثبت های واقعی بر هر چیزی که باید مثبت پیش بینی می شد محاسبه می شود.

$$
recall = \frac{\text{مورد مثبت واقعی}}{\text{مورد مثبت واقعی} + \text{منفی های غلط}}
$$

4. امتیاز F1: متعادل است یا میانگین هارمونیک دقت و یادآوری کمترین مقدار 0 و بیشترین مقدار 1 است. When f1-score برابر با 1 است، به این معنی است که همه کلاس ها به درستی پیش بینی شده اند – این یک امتیاز بسیار سخت برای به دست آوردن با داده های واقعی است (تقریبا همیشه استثنا وجود دارد).

$$
\text{f1-score} = 2* \frac{\text{precision} * \text{recall}}{\text{precision} + \text{recal}}
$$

ما قبلاً با ماتریس سردرگمی، دقت، فراخوانی و معیارهای امتیاز F1 آشنا شده ایم. برای محاسبه آنها می توانیم import Scikit-Learn’s metrics کتابخانه این کتابخانه شامل classification_report و confusion_matrix روش، روش گزارش طبقه بندی امتیاز دقت، فراخوانی و f1 را برمی گرداند. هر دو classification_report و confusion_matrix می توان به راحتی برای یافتن مقادیر برای تمام آن معیارهای مهم استفاده کرد.

برای محاسبه معیارها، ما import روش ها، آنها را فراخوانی کرده و طبقه بندی های پیش بینی شده را به عنوان آرگومان ارسال کنید، y_test، و برچسب های طبقه بندی، یا y_true.

برای تجسم بهتر ماتریس سردرگمی، می‌توانیم آن را در Seaborn ترسیم کنیم heatmap همراه با حاشیه نویسی کمی، و برای گزارش طبقه بندی، بهتر است print نتیجه آن، بنابراین نتایج آن قالب بندی می شود. این کد زیر است:

from sklearn.metrics import classification_report, confusion_matrix

cm = confusion_matrix(y_test,y_pred)
sns.heatmap(cm, annot=True, fmt='d').set_title('Confusion matrix of linear SVM') 

print(classification_report(y_test,y_pred))

این نمایش می دهد:

                precision    recall  f1-score   support

           0       0.99      0.99      0.99       148
           1       0.98      0.98      0.98       127

    accuracy                           0.99       275
   macro avg       0.99      0.99      0.99       275
weighted avg       0.99      0.99      0.99       275

در گزارش طبقه بندی، می دانیم که دقت 0.99، فراخوانی 0.99 و امتیاز f1 0.99 برای اسکناس های جعلی یا کلاس 0 وجود دارد. این اندازه گیری ها با استفاده از 148 نمونه همانطور که در ستون پشتیبانی نشان داده شده است، به دست آمد. در همین حال، برای کلاس 1، یا نت های واقعی، نتیجه یک واحد پایین تر، 0.98 دقت، 0.98 از یادآوری، و همان امتیاز f1 بود. این بار از 127 اندازه گیری تصویر برای به دست آوردن این نتایج استفاده شد.

اگر به ماتریس سردرگمی نگاه کنیم، همچنین می بینیم که از 148 نمونه کلاس 0، 146 نمونه به درستی طبقه بندی شده اند و 2 نمونه مثبت کاذب وجود دارد، در حالی که برای 127 نمونه کلاس 1، 2 نمونه منفی کاذب و 125 نمونه مثبت واقعی وجود دارد.

ما می توانیم گزارش طبقه بندی و ماتریس سردرگمی را بخوانیم، اما آنها به چه معنا هستند؟

تفسیر نتایج

برای فهمیدن معنی، بیایید تمام معیارها را با هم بررسی کنیم.

تقریباً تمام نمونه‌های کلاس 1 به درستی طبقه‌بندی شده بودند، 2 اشتباه برای مدل ما هنگام شناسایی اسکناس‌های واقعی وجود داشت. این همان 0.98 یا 98 درصد است. چیزی مشابه را می توان در مورد کلاس 0 گفت، تنها 2 نمونه به اشتباه طبقه بندی شده اند، در حالی که 148 نمونه منفی واقعی هستند که در مجموع دقت 99٪ را به دست می آورند.

علاوه بر این نتایج، سایر نتایج 0.99 را علامت گذاری می کنند که تقریباً 1 است، یک متریک بسیار بالا. اغلب اوقات، زمانی که چنین متریک بالایی با داده های واقعی اتفاق می افتد، ممکن است نشان دهنده مدلی باشد که بیش از حد با داده ها تنظیم شده است، یا بیش از حد نصب شده.

هنگامی که بیش از حد وجود دارد، مدل ممکن است هنگام پیش‌بینی داده‌هایی که قبلاً شناخته شده‌اند به خوبی کار کند، اما توانایی تعمیم به داده‌های جدید را که در سناریوهای دنیای واقعی مهم است، از دست می‌دهد.

یک آزمایش سریع برای یافتن اینکه آیا اضافه فیت اتفاق می‌افتد نیز با داده‌های قطار است. اگر مدل تا حدودی داده های قطار را به خاطر بسپارد، معیارها بسیار نزدیک به 1 یا 100٪ خواهد بود. به یاد داشته باشید که داده‌های قطار بزرگ‌تر از داده‌های آزمایشی هستند – به همین دلیل – سعی کنید به طور متناسب به آن نگاه کنید، نمونه‌های بیشتر، احتمال اشتباه بیشتر، مگر اینکه مقداری بیش از حد وجود داشته باشد.

برای پیش‌بینی با داده‌های قطار، می‌توانیم کاری را که برای داده‌های آزمایشی انجام داده‌ایم، اما اکنون با X_train:

y_pred_train = svc.predict(X_train)

cm_train = confusion_matrix(y_train,y_pred_train)
sns.heatmap(cm_train, annot=True, fmt='d').set_title('Confusion matrix of linear SVM with train data')

print(classification_report(y_train,y_pred_train))

این خروجی:

                precision    recall  f1-score   support

           0       0.99      0.99      0.99       614
           1       0.98      0.99      0.99       483

    accuracy                           0.99      1097
   macro avg       0.99      0.99      0.99      1097
weighted avg       0.99      0.99      0.99      1097

به راحتی می توان دید که به نظر می رسد بیش از حد تناسب وجود دارد، زمانی که معیارهای قطار 99٪ در هنگام داشتن 4 برابر داده بیشتر باشد. در این سناریو چه کاری می توان انجام داد؟

برای برگرداندن بیش از حد، می‌توانیم مشاهدات قطار بیشتری اضافه کنیم، از یک روش آموزش با بخش‌های مختلف مجموعه داده استفاده کنیم، مانند اعتبار سنجی متقابلو همچنین پارامترهای پیش‌فرض را که قبلاً قبل از آموزش وجود دارد، هنگام ایجاد مدل ما یا تغییر دهید هایپرپارامترها. بیشتر اوقات، Scikit-learn برخی از پارامترها را به عنوان پیش‌فرض تنظیم می‌کند، و اگر زمان زیادی برای خواندن اسناد اختصاص داده نشود، می‌تواند بی‌صدا اتفاق بیفتد.

می توانید قسمت دوم این راهنما را بررسی کنید (به زودی!) برای مشاهده روش پیاده سازی اعتبار متقاطع و انجام تنظیم هایپرپارامتر.

نتیجه

در این مقاله به بررسی هسته خطی ساده SVM پرداختیم. ما شهود پشت الگوریتم SVM را دریافت کردیم، از یک مجموعه داده واقعی استفاده کردیم، داده ها را بررسی کردیم و دیدیم که چگونه می توان از این داده ها همراه با SVM با پیاده سازی آن با کتابخانه Scikit-Learn پایتون استفاده کرد.

برای ادامه تمرین، می توانید سایر مجموعه داده های دنیای واقعی موجود در مکان هایی مانند کاگل، UCI، مجموعه داده های عمومی Big Query، دانشگاه ها و وب سایت های دولتی.

همچنین پیشنهاد می‌کنم ریاضیات واقعی پشت مدل SVM را بررسی کنید. اگرچه برای استفاده از الگوریتم SVM لزوماً به آن نیاز ندارید، اما هنوز هم بسیار مفید است که بدانید واقعاً چه چیزی در حال انجام است. روی در پشت صحنه در حالی که الگوریتم شما در حال یافتن مرزهای تصمیم است.

اگر می خواهید به یادگیری در مورد SVM ها ادامه دهید، می توانید به قسمت دوم این مجموعه، یعنی درک فراپارامترهای SVM بروید.