رگرسیون خطی در پایتون با Scikit-Learn

اگر بیشتر مطالعه می کردید، آیا نمرات کلی شما بهتر می شد؟

یکی از راه های پاسخ به این سوال، داشتن داده است روی چه مدت درس خوانده اید و چه امتیازی کسب کرده اید. سپس می‌توانیم ببینیم آیا الگوی در آن داده وجود دارد یا خیر، و اگر در آن الگو، وقتی به ساعت‌ها اضافه می‌کنید، در نهایت به درصد امتیازات نیز اضافه می‌شود.

به عنوان مثال، فرض کنید یک مجموعه داده با امتیاز ساعت دارید که شامل ورودی هایی مانند 1.5 ساعت و امتیاز 87.5٪ است. همچنین می تواند شامل 1.61h، 2.32h و 78%، 97% نمرات باشد. نوع داده ای که می تواند هر مقدار میانی (یا هر سطحی از دانه بندی) داشته باشد به عنوان شناخته می شود مداوم داده ها.

سناریوی دیگر این است که شما یک مجموعه داده امتیاز ساعتی دارید که به جای نمرات مبتنی بر اعداد، شامل نمرات بر اساس حروف است، مانند A، B یا C. نمرات مقادیر واضحی هستند که می‌توان آنها را جدا کرد، زیرا نمی‌توانید A داشته باشید. 23 ، A ++++++++++ (و به Infinity) یا A * E^12. نوع داده ای که نمی توان آن را پارتیشن بندی کرد یا به صورت دانه بندی تعریف کرد به عنوان شناخته می شود گسسته داده ها.

مستقر روی روش (شکل) داده های شما – برای اینکه بفهمید بر اساس چه نمره ای خواهید گرفت روی زمان مطالعه شما – شما اجرا خواهید کرد پسرفت یا طبقه بندی.

رگرسیون انجام می شود روی داده های پیوسته، در حالی که طبقه بندی انجام می شود روی داده های گسسته. رگرسیون می تواند هر چیزی باشد، از پیش بینی سن یک فرد، قیمت خانه یا ارزش هر متغیر. طبقه بندی شامل پیش بینی چه چیزی است کلاس چیزی به آن تعلق دارد (مانند خوش خیم یا بدخیم بودن تومور).

اگر می‌خواهید از طریق پروژه‌های عملی در دنیای واقعی، نمونه‌برداری شده، یاد بگیرید، ما را بررسی کنید “پیش بینی عملی قیمت خانه – یادگیری ماشینی در پایتون” و درجه پژوهشی ما “طبقه بندی سرطان سینه با یادگیری عمیق – Keras و TensorFlow”!

هم برای رگرسیون و هم برای طبقه بندی – از داده ها برای پیش بینی استفاده می کنیم برچسب ها (اصطلاح چتر برای متغیرهای هدف). برچسب ها می توانند هر چیزی از “B” (کلاس) برای کارهای طبقه بندی تا 123 (تعداد) برای وظایف رگرسیونی باشند. از آنجا که ما همچنین برچسب ها را عرضه می کنیم – اینها هستند یادگیری تحت نظارت الگوریتم ها

در این راهنمای مبتدی – ما با استفاده از کتابخانه Scikit-Learn، رگرسیون خطی را در پایتون انجام خواهیم داد. ما از یک خط لوله یادگیری ماشینی سرتاسری عبور خواهیم کرد. ابتدا داده‌هایی را که از آن‌ها یاد می‌گیریم، بارگذاری می‌کنیم و آن‌ها را تجسم می‌کنیم، در همان زمان اجرا می‌کنیم تجزیه و تحلیل داده های اکتشافی. سپس، داده‌ها را از قبل پردازش می‌کنیم و مدل‌هایی متناسب با آن‌ها (مانند دستکش) می‌سازیم. سپس این مدل ارزیابی می‌شود و در صورت مطلوب بودن، برای پیش‌بینی مقادیر جدید استفاده می‌شود روی ورودی جدید

تجزیه و تحلیل داده های اکتشافی

بیایید با تجزیه و تحلیل داده های اکتشافی شروع کنیم. شما می‌خواهید ابتدا داده‌های خود را بشناسید – این شامل بارگیری آن‌ها، تجسم ویژگی‌ها، کاوش در روابط آنها و ساختن فرضیه‌ها می‌شود. روی مشاهدات شما مجموعه داده یک فایل CSV (مقادیر جدا شده با کاما) است که شامل ساعت های مطالعه شده و امتیازات به دست آمده بر اساس است. روی آن ساعت ها ما داده ها را در a بارگذاری خواهیم کرد DataFrame استفاده از پاندا:

import pandas as pd

اگر تازه وارد پاندا هستید و DataFrames، ما را بخوانید “راهنمای پایتون با پانداها: آموزش DataFrame با مثال”!

بیایید پرونده CSV را بخوانیم و آن را در یک DataFrame:

path_to_file = 'home/projects/datasets/student_scores.csv'
df = pd.read_csv(path_to_file)

پس از بارگیری داده ها، بیایید با استفاده از 5 مقدار اول نگاهی کوتاه بیندازیم head() روش:

df.head() 

این منجر به:

   Hours  Scores
0    2.5      21
1    5.1      47
2    3.2      27
3    8.5      75
4    3.5      30

همچنین می‌توانیم شکل مجموعه داده خود را از طریق shape ویژگی:

df.shape

دانستن شکل داده ها به طور کلی برای اینکه بتوانید آن ها را تجزیه و تحلیل کنید و مدل هایی پیرامون آن بسازید بسیار مهم است:

(25, 2)

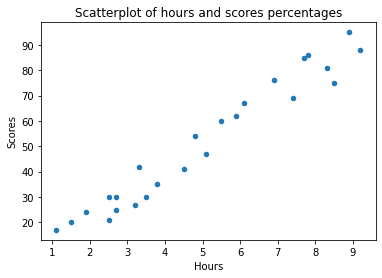
ما 25 سطر و 2 ستون داریم – 25 ورودی حاوی یک جفت ساعت و الف نمره. سوال اولیه ما این بود که آیا اگر بیشتر درس بخوانیم، نمره بالاتری می‌گیریم؟ در اصل، ما خواستار رابطه بین هستیم ساعت ها و امتیازات. بنابراین، چه رابطه ای بین این متغیرها وجود دارد؟ یک راه عالی برای کشف روابط بین متغیرها از طریق توطئه های پراکندگی است. ما ساعت ها را ترسیم می کنیم روی محور X و امتیازات روی محور Y، و برای هر جفت، یک نشانگر بر اساس قرار خواهد گرفت روی ارزش های آنها:

df.plot.scatter(x='Hours', y='Scores', title='Scatter Plot of hours and scores percentages');

اگر تازه وارد توطئه ها هستید – ما را بخوانید “نقشه پراکندگی Matplotlib – آموزش و مثال”!

این منجر به:

با افزایش ساعت ها، نمرات نیز افزایش می یابد. در اینجا یک همبستگی مثبت نسبتاً بالایی وجود دارد! از آنجا که شکل خطی که نقاط ایجاد می کنند مستقیم به نظر می رسد – ما می گوییم که وجود دارد همبستگی خطی مثبت بین متغیرهای ساعت و امتیاز. چقدر به هم مرتبط هستند؟ را corr() روش همبستگی بین متغیرهای عددی را در a محاسبه و نمایش می دهد DataFrame:

print(df.corr())

           Hours    Scores
Hours   1.000000  0.976191
Scores  0.976191  1.000000

در این جدول ، ساعت ها و ساعت ها 1.0 (100 ٪) همبستگی ، همانطور که نمرات همبستگی 100 ٪ با نمرات دارند ، به طور طبیعی. هر متغیر یک نقشه برداری 1: 1 با خودش خواهد داشت! با این حال ، همبستگی بین نمرات و ساعت ها است 0.97. هر چیزی بالاتر 0.8 به عنوان یک همبستگی مثبت قوی در نظر گرفته می شود.

اگر می خواهید اطلاعات بیشتری در مورد همبستگی بین متغیرهای خطی با جزئیات و همچنین ضرایب همبستگی مختلف بخوانید ، ما را بخوانید “محاسبه ضریب همبستگی پیرسون در پایتون با numpy”!

داشتن یک همبستگی خطی بالا به این معنی است که ما به طور کلی قادر خواهیم بود مقدار یک ویژگی را بر اساس بگوییم روی دیگری. حتی بدون محاسبه ، می توانید بگویید که اگر کسی 5 ساعت تحصیل کند ، آنها به عنوان نمره خود حدود 50 ٪ دریافت می کنند. از آنجا که این رابطه واقعاً قوی است – ما می توانیم یک الگوریتم رگرسیون خطی ساده و در عین حال دقیق را برای پیش بینی نمره ایجاد کنیم روی زمان مطالعه، روی این مجموعه داده

وقتی بین دو متغیر رابطه خطی داشته باشیم ، به یک خط خواهیم پرداخت. وقتی رابطه خطی بین سه ، چهار ، پنج (یا بیشتر) وجود داشته باشد ، ما به دنبال یک تقاطع هواپیماها. در هر صورت ، این نوع کیفیت در جبر تعریف می شود خطی بودن.

پاندا همچنین برای خلاصه های آماری با یک روش یاور عالی ارسال می شود و ما می توانیم describe() مجموعه داده برای دریافت ایده ای از مقادیر میانگین، حداکثر، حداقل و غیره ستون های ما:

print(df.describe())

           Hours     Scores
count  25.000000  25.000000
mean    5.012000  51.480000
std     2.525094  25.286887
min     1.100000  17.000000
25%     2.700000  30.000000
50%     4.800000  47.000000
75%     7.400000  75.000000
max     9.200000  95.000000

نظریه رگرسیون خطی

متغیرهای ما یک رابطه خطی را بیان می کنند. ما به طور شهودی می توانیم بر اساس درصد امتیاز را حدس بزنیم روی تعداد ساعات مطالعه با این حال، آیا می توانیم روش رسمی تری برای این کار تعریف کنیم؟ اگر یک خط عمودی را از مقدار معینی از “Hours” ترسیم کنیم، می‌توانیم یک خط بین نقاط خود ترسیم کنیم و مقدار “امتیاز” را بخوانیم:

معادله ای که هر خط مستقیم را توصیف می کند:
$$
y = a*x+b
$$
در این معادله، y نشان دهنده درصد امتیاز است، x نشان دهنده ساعات مطالعه است. b جایی است که خط از محور Y شروع می شود که به آن محور Y نیز می گویند رهگیری و a مشخص می کند که آیا خط قرار است بیشتر به سمت قسمت بالایی یا پایینی نمودار (زاویه خط) باشد، بنابراین به آن خط می گویند. شیب از خط

با تنظیم شیب و رهگیری از خط، ما می توانیم آن را در هر جهت حرکت دهیم. بنابراین – با تعیین مقادیر شیب و فاصله، می‌توانیم یک خط را متناسب با داده‌هایمان تنظیم کنیم!

خودشه! این قلب رگرسیون خطی است و یک الگوریتم واقعاً فقط مقادیر شیب و قطع را مشخص می کند. از مقادیر استفاده می کند x و y که ما قبلاً داریم و مقادیر آن را تغییر می دهد a و b. با انجام این کار، چندین خط را به نقاط داده منطبق می کند و خطی را که به تمام نقاط داده نزدیکتر است، برمی گرداند. بهترین خط مناسب. با مدل سازی آن رابطه خطی، الگوریتم رگرسیون ما a نیز نامیده می شود مدل. در این process، زمانی که سعی می کنیم تعیین کنیم، یا پیش بینی بر اساس درصد روی ساعت، به این معنی است که ما y متغیر بستگی دارد روی ارزش های ما x متغیر.

رگرسیون خطی با Python’s Scikit-Learn

با تئوری زیر کمربند ما – بیایید به پیاده سازی یک الگوریتم رگرسیون خطی با پایتون و کتابخانه Scikit-Learn برسیم! ما با یک رگرسیون خطی ساده‌تر شروع می‌کنیم و سپس گسترش می‌دهیم رگرسیون خطی چندگانه با مجموعه داده جدید

پیش پردازش داده ها

در بخش قبلی، ما قبلا پانداها را وارد کرده ایم، فایل خود را در a بارگذاری کرده ایم DataFrame و یک نمودار رسم کرد تا ببیند آیا نشانه ای از رابطه خطی وجود دارد یا خیر. اکنون می‌توانیم داده‌های خود را به دو آرایه تقسیم کنیم – یکی برای ویژگی وابسته و دیگری برای ویژگی مستقل یا هدف. از آنجایی که می خواهیم بسته به درصد امتیاز را پیش بینی کنیم روی ساعات مطالعه، ما y خواهد بود “نمره” ستون و ما X خواهد شد “ساعت ها” ستون

برای جداسازی هدف و ویژگی‌ها، می‌توانیم مقادیر ستون dataframe را به ما نسبت دهیم y و X متغیرها:

y = df('Scores').values.reshape(-1, 1)
X = df('Hours').values.reshape(-1, 1)

مدل رگرسیون خطی Scikit-Learn یک ورودی دوبعدی را انتظار دارد و اگر فقط مقادیر را استخراج کنیم، واقعاً یک آرایه 1 بعدی ارائه می دهیم:

print(df('Hours').values) 
print(df('Hours').values.shape) 

انتظار ورودی 2 بعدی را دارد زیرا LinearRegression() کلاس (بیشتر روی بعداً) ورودی‌هایی را انتظار دارد که ممکن است بیش از یک مقدار داشته باشند (اما می‌توانند یک مقدار نیز باشند). در هر صورت – باید یک آرایه دو بعدی باشد، جایی که هر عنصر (ساعت) در واقع یک آرایه 1 عنصری است:

print(X.shape) 
print(X)      

ما قبلاً می توانستیم غذای خود را تغذیه کنیم X و y داده‌ها مستقیماً به مدل رگرسیون خطی ما می‌رسد، اما اگر از همه داده‌های خود به‌طور هم‌زمان استفاده کنیم، چگونه می‌توانیم بفهمیم که نتایج ما خوب است؟ درست مانند یادگیری، کاری که ما انجام خواهیم داد، استفاده از بخشی از داده ها است قطار – تعلیم دادن مدل ما و بخشی دیگر از آن، به تست آی تی.

اگر می‌خواهید درباره قوانین کلی، اهمیت تقسیم مجموعه‌ها، مجموعه‌های اعتبارسنجی و train_test_split() روش کمکی، راهنمای مفصل ما را بخوانید روی “Scikit-Learn’s train_test_split() – مجموعه های آموزش، تست و اعتبارسنجی”!

این به راحتی از طریق کمک کننده به دست می آید train_test_split() روشی که ما را می پذیرد X و y آرایه ها (همچنین کار می کند روی DataFrames و یک تک را تقسیم می کند DataFrame در مجموعه های آموزشی و آزمایشی) و الف test_size. را test_size درصدی از داده های کلی است که برای آزمایش استفاده خواهیم کرد:

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

این روش به طور تصادفی با توجه به درصدی که ما تعریف کرده‌ایم، نمونه‌ها را می‌گیرد، اما به جفت‌های Xy احترام می‌گذارد، مبادا نمونه‌برداری به طور کامل رابطه را با هم مخلوط کند. برخی از تقسیم‌بندی‌های آزمون قطار رایج هستند 80/20 و 70/30.

از زمان نمونه گیری process ذاتا است تصادفی، هنگام اجرای متد همیشه نتایج متفاوتی خواهیم داشت. تا بتوانیم نتایج یکسانی داشته باشیم یا قابل تکرار در نتیجه، می‌توانیم یک ثابت به نام تعریف کنیم SEED که ارزش معنای زندگی را دارد (42):

SEED = 42

سپس می توانیم از آن عبور کنیم SEEDبه random_state پارامتر ما train_test_split روش:

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = SEED)

حالا اگر شما print شما X_train آرایه – ساعت مطالعه را پیدا خواهید کرد و y_train شامل درصدهای امتیازی است:

print(X_train) 
print(y_train) 

آموزش مدل رگرسیون خطی

ما مجموعه های قطار و تست خود را آماده کرده ایم. Scikit-Learn انواع مدل های زیادی دارد که به راحتی می توانیم import و قطار، LinearRegression یکی از آنها بودن:

from sklearn.linear_model import LinearRegression
regressor = LinearRegression()

اکنون، ما باید خط را با داده‌های خود مطابقت دهیم، این کار را با استفاده از آن انجام خواهیم داد .fit() روش همراه با ما X_train و y_train داده ها:

regressor.fit(X_train, y_train)

اگر خطایی وجود نداشته باشد – واپسگرا بهترین خط مناسب را پیدا کرده است! خط با ویژگی های ما و رهگیری/شیب تعریف می شود. در واقع، ما می‌توانیم با چاپ کردن، رهگیری و شیب را بررسی کنیم regressor.intecept_ و regressor.coef_ صفات به ترتیب:

print(regressor.intercept_)

2.82689235

برای بازیابی شیب (که همچنین ضریب از x):

print(regressor.coef_)

نتیجه باید این باشد:

(9.68207815)

این به معنای واقعی کلمه می تواند از قبل به فرمول ما متصل شود:

$$
امتیاز = 9.68207815*ساعت+2.82689235
$$

بیایید به سرعت بررسی کنیم که آیا این با حدس ما مطابقت دارد یا خیر:

$$\begin{array}{c}\mathrm{ساعت}o\mathrm{تو}rس=5\\ سجorه=9.68207815\ast \mathrm{ساعت}o\mathrm{تو}rس+2.82689235\\ سجorه=51.2672831\end{array}$$

با 5 ساعت مطالعه، می توانید انتظار 51% را به عنوان نمره داشته باشید! روش دیگر برای تفسیر مقدار رهگیری این است – اگر دانش آموزی یک ساعت بیشتر از آنچه قبلاً برای امتحان مطالعه کرده است مطالعه کند، می تواند انتظار داشته باشد که افزایشی از آن داشته باشد. 9.68٪ با توجه به درصد امتیازی که قبلاً کسب کرده بودند.

به عبارت دیگر، مقدار شیب را نشان می دهد چه اتفاقی برای متغیر وابسته می افتد هر زمان که وجود دارد افزایش یا کاهش) از یک واحد از متغیر مستقل.

پیشگویی

برای جلوگیری از اجرای محاسبات خودمان، می‌توانیم فرمول خودمان را بنویسیم که مقدار را محاسبه می‌کند:

def calc(slope, intercept, hours):
    return slope*hours+intercept

score = calc(regressor.coef_, regressor.intercept_, 9.5)
print(score) 

با این حال – یک راه بسیار راحت تر برای پیش بینی مقادیر جدید با استفاده از مدل ما فراخوانی است روی را predict() تابع:

score = regressor.predict(((9.5)))
print(score) 

نتیجه ما این است 94.80663482، یا تقریباً 95%. اکنون ما برای هر ساعتی که فکرش را می کنیم یک تخمین درصد امتیاز داریم. اما آیا می توانیم به این تخمین ها اعتماد کنیم؟ در پاسخ به این سوال دلیل این است که چرا ما در وهله اول داده ها را به آموزش و آزمایش تقسیم می کنیم. اکنون می‌توانیم با استفاده از داده‌های آزمایشی خود پیش‌بینی کنیم و نتایج پیش‌بینی‌شده را با نتایج واقعی خود مقایسه کنیم حقیقت زمین نتایج.

برای پیش بینی روی داده های آزمون، ما عبور می کنیم X_test مقادیر به predict() روش. می توانیم نتایج را به متغیر اختصاص دهیم y_pred:

y_pred = regressor.predict(X_test)

را y_pred متغیر اکنون شامل تمام مقادیر پیش بینی شده برای مقادیر ورودی در است X_test. اکنون می‌توانیم مقادیر خروجی واقعی را با هم مقایسه کنیم X_test با مقادیر پیش بینی شده، با مرتب کردن آنها در کنار هم در یک ساختار چارچوب داده:

df_preds = pd.DataFrame({'Actual': y_test.squeeze(), 'Predicted': y_pred.squeeze()})
print(df_preds

خروجی به شکل زیر است:

   Actual  Predicted
0      81  83.188141
1      30  27.032088
2      21  27.032088
3      76  69.633232
4      62  59.951153

اگرچه به نظر می رسد مدل ما خیلی دقیق نیست، اما درصدهای پیش بینی شده به درصد واقعی نزدیک است. بیایید تفاوت بین مقادیر واقعی و پیش بینی شده را کمی کنیم تا دیدی عینی از روش عملکرد واقعی آن بدست آوریم.

ارزیابی مدل

پس از مشاهده داده‌ها، دیدن یک رابطه خطی، آموزش و آزمایش مدل خود، می‌توانیم با استفاده از برخی از آن‌ها بفهمیم که چقدر خوب پیش‌بینی می‌کند. معیارهای. برای مدل های رگرسیون، سه معیارهای ارزیابی عمدتا مورد استفاده قرار می گیرند:

1. میانگین خطای مطلق (MAE): وقتی مقادیر پیش بینی شده را از مقادیر واقعی کم می کنیم، خطاها را به دست می آوریم، مقادیر مطلق آن خطاها را جمع کرده و میانگین آنها را بدست می آوریم. این متریک تصوری از خطای کلی برای هر پیش‌بینی مدل ارائه می‌دهد، هرچه کوچکتر (نزدیک به صفر) بهتر باشد.

$$
mae = (\frac{1}{n})\sum_{i=1}^{n}\left | واقعی – پیش بینی شده \right |
$$

2. خطای متوسط ​​مربع (MSE): شبیه به متریک MAE است، اما مقادیر مطلق خطاها را مربع می کند. همچنین ، مانند MAE ، هر چه کوچکتر یا نزدیک به 0 ، بهتر است. مقدار MSE به گونه ای مربع است که خطاهای بزرگ را حتی بزرگتر می کند. نکته ای که باید به آن دقت کرد، این است که معمولاً به دلیل اندازه مقادیر آن و این واقعیت که آنها در مقیاس یکسانی از داده ها نیستند، تفسیر آن سخت است.

$$
mse = \sum_{i=1}^{D}(واقعی – پیش بینی شده)^2
$$

3. ریشه میانگین مربعات خطا (RMSE): سعی می کند با بدست آوردن مربع، مشکل تفسیر مطرح شده در MSE را حل کند root از مقدار نهایی آن ، به گونه ای که آن را به همان واحدهای داده بازگرداند. تفسیر ساده تر و خوب است وقتی نیاز به نمایش یا نشان دادن مقدار واقعی داده ها با خطا داریم. این نشان می‌دهد که داده‌ها چقدر ممکن است متفاوت باشند، بنابراین، اگر RMSE 4.35 داشته باشیم، مدل ما می‌تواند خطا داشته باشد یا به این دلیل که 4.35 را به مقدار واقعی اضافه کرده است یا برای رسیدن به مقدار واقعی به 4.35 نیاز دارد. هرچه به 0 نزدیکتر باشد، بهتر است.

$$
rmse = \sqrt{ \sum_{i=1}^{D}(واقعی – پیش بینی شده)^2}
$$

ما می توانیم از هر یک از این سه معیار استفاده کنیم مقایسه کنید مدل ها (در صورت نیاز به انتخاب یکی). ما همچنین می توانیم مدل رگرسیون یکسان را با مقادیر مختلف استدلال یا با داده های مختلف مقایسه کنیم و سپس معیارهای ارزیابی را در نظر بگیریم. این به عنوان شناخته شده است تنظیم هایپرپارامتر – تنظیم HyperParameters که بر یک الگوریتم یادگیری تأثیر می گذارد و نتایج را مشاهده می کند.

هنگام انتخاب بین مدل ها ، مواردی که کوچکترین خطاها را دارند معمولاً عملکرد بهتری دارند. هنگام پایش مدل‌ها، اگر معیارها بدتر می‌شد، نسخه قبلی مدل بهتر بود، یا تغییرات قابل‌توجهی در داده‌ها وجود داشت که مدل بدتر از عملکردش بود.

خوشبختانه ، ما مجبور نیستیم هیچ یک از محاسبات معیارها را به صورت دستی انجام دهیم. بسته Scikit-Learn در حال حاضر با توابع همراه است که می تواند برای یافتن مقادیر این معیارها برای ما استفاده شود. بیایید مقادیر این معیارها را با استفاده از داده های آزمون خود پیدا کنیم. اول، ما خواهیم کرد import ماژول های لازم برای محاسبه خطاهای MAE و MSE. به ترتیب، mean_absolute_error و mean_squared_error:

from sklearn.metrics import mean_absolute_error, mean_squared_error

اکنون ، ما می توانیم MAE و MSE را با عبور از آن محاسبه کنیم y_test (واقعی) و y_pred (پیش بینی شده) به روش ها. RMSE را می توان با گرفتن مربع محاسبه کرد root از MSE، برای آن، از NumPy استفاده خواهیم کرد sqrt() روش:

import numpy as np

برای محاسبات متریک:

mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)

ما نیز خواهیم کرد print نتایج معیارها با استفاده از f رشته و دقت 2 رقمی پس از کاما با :.2f:

print(f'Mean absolute error: {mae:.2f}')
print(f'Mean squared error: {mse:.2f}')
print(f'Root mean squared error: {rmse:.2f}')

نتایج اندازه گیری ها به صورت زیر خواهد بود:

Mean absolute error: 3.92
Mean squared error: 18.94
Root mean squared error: 4.35

همه خطاهای ما کم هستند – و مقدار واقعی را حداکثر تا 4.35 (کمتر یا بیشتر) از دست می دهیم، که با توجه به داده هایی که داریم، محدوده بسیار کمی است.

رگرسیون خطی چندگانه

تا این مرحله ، ما با استفاده از تنها یک متغیر ، مقداری را با رگرسیون خطی پیش بینی کرده ایم. سناریوی متفاوتی وجود دارد که می توانیم در نظر بگیریم ، جایی که می توانیم استفاده از آن را پیش بینی کنیم بسیاری از متغیرها به جای یک ، و این همچنین یک سناریوی بسیار متداول در زندگی واقعی است ، جایی که بسیاری از موارد می توانند بر برخی نتیجه تأثیر بگذارند.

به عنوان مثال، اگر بخواهیم مصرف گاز را در ایالت های ایالات متحده پیش بینی کنیم، استفاده از تنها یک متغیر، به عنوان مثال، مالیات بر گاز برای انجام آن محدود کننده خواهد بود، زیرا چیزی بیش از مالیات بر گاز بر مصرف تأثیر می گذارد. در مصرف گاز چیزهایی بیش از مالیات گاز دخیل است، مانند درآمد سرانه مردم در یک منطقه خاص، گسترش بزرگراه های آسفالته، نسبت جمعیتی که گواهینامه رانندگی دارند و بسیاری عوامل دیگر. برخی از عوامل بیشتر از دیگران بر مصرف تأثیر می گذارند – و اینجاست که ضرایب همبستگی واقعاً کمک می کند!

در چنین موردی، زمانی که استفاده از چندین متغیر منطقی است، رگرسیون خطی به a تبدیل می‌شود رگرسیون خطی چندگانه.

معمولاً داده‌های دنیای واقعی، با داشتن متغیرهای بسیار بیشتر با مقادیر بیشتر، محدوده یا بیشتر است تغییرپذیریو همچنین روابط پیچیده بین متغیرها – شامل رگرسیون خطی چندگانه به جای رگرسیون خطی ساده خواهد بود.

که این است که بگوییم، روی به صورت روزانه، اگر خطی بودن داده های شما وجود داشته باشد، احتمالاً یک رگرسیون خطی چندگانه برای داده های خود اعمال خواهید کرد.

تجزیه و تحلیل داده های اکتشافی

برای درک عملی رگرسیون خطی چندگانه، اجازه دهید به کار با مثال مصرف گاز خود ادامه دهیم و از مجموعه داده ای استفاده کنیم که داده مصرف گاز دارد. روی 48 ایالت ایالات متحده.

به دنبال کاری که با رگرسیون خطی انجام دادیم، قبل از اعمال رگرسیون خطی چندگانه نیز می خواهیم داده های خود را بدانیم. اول، ما می توانیم import داده ها با پاندا read_csv() روش:

path_to_file = 'home/projects/datasets/petrol_consumption.csv'
df = pd.read_csv(path_to_file)

اکنون می توانیم به پنج ردیف اول نگاهی بیندازیم df.head():

df.head()

این منجر به:

    Petrol_tax	Average_income	Paved_Highways	Population_Driver_licence(%)  Petrol_Consumption
0	9.0			3571			1976			0.525						  541
1	9.0			4092			1250			0.572						  524
2	9.0			3865			1586			0.580						  561
3	7.5			4870			2351			0.529						  414
4	8.0			4399			431				0.544						  410

ما می توانیم ببینیم که داده های ما دارای چند ردیف و ستون هستند shape:

df.shape

که نمایش می دهد:

(48, 5)

در این مجموعه داده 48 سطر و 5 ستون داریم. هنگام طبقه بندی اندازه یک مجموعه داده، بین آمار و علوم کامپیوتر نیز تفاوت هایی وجود دارد.

در آمار، یک مجموعه داده با بیش از 30 یا با بیش از 100 ردیف (یا مشاهدات) در حال حاضر بزرگ در نظر گرفته می شود، در حالی که در علوم کامپیوتر، یک مجموعه داده معمولاً باید حداقل 1000-3000 ردیف داشته باشد تا “بزرگ” در نظر گرفته شود. “بزرگ” نیز بسیار ذهنی است – برخی 3000 را بزرگ می دانند در حالی که برخی 3000000 را بزرگ می دانند.

هیچ اتفاق نظری وجود ندارد روی اندازه مجموعه داده ما. بیایید به بررسی آن ادامه دهیم و نگاهی به آمار توصیفی این داده های جدید بیندازیم. این بار، مقایسه آمار را با گرد کردن مقادیر به دو اعشار با عدد آسان می کنیم round() روش، و جابجایی جدول با T ویژگی:

print(df.describe().round(2).T)

جدول ما اکنون به جای اینکه در عرض ردیف باشد، به صورت ستونی است:

                             count mean	   std	   min	   25%	   50%	   75%	   max
Petrol_tax					 48.0  7.67	   0.95	   5.00	   7.00	   7.50	   8.12	   10.00
Average_income				 48.0  4241.83 573.62  3063.00 3739.00 4298.00 4578.75 5342.00
Paved_Highways				 48.0  5565.42 3491.51 431.00  3110.25 4735.50 7156.00 17782.00
Population_Driver_licence(%) 48.0  0.57	   0.06	   0.45	   0.53	   0.56	   0.60	   0.72
Petrol_Consumption			 48.0  576.77  111.89  344.00  509.50  568.50  632.75  968.00

با نگاه کردن به دقیقه و حداکثر ستون های جدول توصیف، می بینیم که حداقل مقدار در داده های ما است 0.45، و حداکثر مقدار است 17,782. این به این معنی است که محدوده داده ما است 17,781.55 (17,782 – 0.45 = 17,781.55)، بسیار گسترده – که به این معنی است که تنوع داده های ما نیز زیاد است.

همچنین با مقایسه مقادیر منظور داشتن و std ستون ها ، مانند 7.67 و 0.95، 4241.83 و 573.62و غیره، می بینیم که ابزار واقعاً با انحرافات استاندارد فاصله دارد. این بدان معناست که داده های ما از میانگین فاصله زیادی دارند، غیر متمرکز – که به تنوع نیز می افزاید.

ما در حال حاضر دو نشانه داریم مبنی بر اینکه داده های ما پراکنده شده است، که به نفع ما نیست، زیرا داشتن خطی که بتواند از 0.45 تا 17782 – از نظر آماری، به سختی برسد. آن تنوع را توضیح دهید.

در هر صورت، همیشه مهم است که داده ها را رسم کنیم. داده ها با اشکال (روابط) متفاوت می توانند آمار توصیفی یکسانی داشته باشند. بنابراین، بیایید به راه خود ادامه دهیم و به نقاط خود در نمودار نگاه کنیم.

مثال دیگری از یکسان بودن ضریب بین روابط مختلف، همبستگی پیرسون است (که بررسی می کند همبستگی خطی):

این داده ها به وضوح دارای یک الگو هستند! اگرچه غیر خطی است و داده ها همبستگی خطی ندارند، بنابراین ضریب پیرسون برابر است با 0 برای بیشتر آنها خواهد بود 0 برای نویز تصادفی نیز.

باز هم، اگر علاقه مند به خواندن اطلاعات بیشتر در مورد ضریب پیرسون هستید، به طور عمیق مطالعه کنید. “محاسبه ضریب همبستگی پیرسون در پایتون با Numpy”!

در سناریوی رگرسیون ساده ما ، ما از یک پراکندگی از متغیرهای وابسته و مستقل استفاده کرده ایم تا ببینیم شکل نقاط نزدیک به یک خط است یا خیر. در سناریوی فعلی ما چهار متغیر مستقل و یک متغیر وابسته داریم. برای انجام یک نمودار پراکندگی با همه متغیرها به یک بعد برای هر متغیر نیاز است، که منجر به یک نمودار 5 بعدی می شود.

ما می توانیم یک نقشه 5D با تمام متغیرها ایجاد کنیم ، که مدتی طول می کشد و خواندن آن کمی سخت خواهد بود – یا می توانیم برای هر یک از متغیرهای مستقل و متغیرهای وابسته خود یک پراکندگی ترسیم کنیم تا ببینیم رابطه خطی بین آنها وجود دارد.

ذیل تیغ اوکام (همچنین به عنوان تیغ ​​اوکام شناخته می شود) و پایتون PEP20 – “ساده بهتر از پیچیده است” – ما یک حلقه for با یک نمودار برای هر متغیر ایجاد خواهیم کرد.

این بار ، ما استفاده خواهیم کرد متولد دریا، یک پسوند Matplotlib که پانداها هنگام ترسیم از آن در زیر کاپوت استفاده می کنند:

import seaborn as sns 

variables = ('Petrol_tax', 'Average_income', 'Paved_Highways','Population_Driver_licence(%)')

for var in variables:
    plt.figure() 
    
    
    
    sns.regplot(x=var, y='Petrol_Consumption', data=df).set(title=f'Regression plot of {var} and Petrol Consumption');

در کد فوق توجه کنید که ما در حال وارد کردن Seaborn هستیم ، لیستی از متغیرهایی را که می خواهیم ترسیم کنیم ایجاد می کنیم و از طریق آن لیست حلقه می کنیم تا هر متغیر مستقل را با متغیر وابسته خود ترسیم کنیم.

طرح Seaborn ما استفاده می کنیم regplot، که کوتاه از طرح رگرسیون. این یک نمودار پراکنده است که داده های پراکنده را به همراه خط رگرسیون ترسیم می کند. اگر ترجیح می دهید به یک نمودار پراکنده بدون خط رگرسیون نگاه کنید، از آن استفاده کنید sns.scatteplot بجای.

این چهار طرح ما هستند:

وقتی به توطئه های reg نگاه می کنیم، به نظر می رسد Petrol_tax و Average_income رابطه خطی منفی ضعیفی با Petrol_Consumption. همچنین به نظر می رسد که Population_Driver_license(%) رابطه خطی مثبت قوی با Petrol_Consumption، و اینکه Paved_Highways متغیر هیچ رابطه ای با Petrol_Consumption.

همچنین می توانیم همبستگی متغیرهای جدید را این بار با استفاده از Seaborn محاسبه کنیم heatmap() به ما کمک کند قوی ترین و ضعیف ترین همبستگی ها را بر اساس تشخیص دهیم روی تن های گرمتر (قرمز) و سردتر (آبی):

correlations = df.corr()

sns.heatmap(correlations, annot=True).set(title='Heat map of Consumption Data - Pearson Correlations');

به نظر می رسد که نقشه حرارتی تحلیل قبلی ما را تایید می کند! Petrol_tax و Average_income یک رابطه خطی منفی ضعیف دارند، به ترتیب، -0.45 و -0.24 با Petrol_Consumption. Population_Driver_license(%) دارای یک رابطه خطی مثبت قوی از 0.7 با Petrol_Consumption، و Paved_Highways همبستگی است 0.019 – که نشان دهنده عدم ارتباط با Petrol_Consumption.

همبستگی دلالت بر علیت ندارد، اما اگر بتوانیم با مدل رگرسیونی خود پدیده ها را با موفقیت توضیح دهیم، ممکن است علیت را پیدا کنیم.

نکته مهم دیگر که باید در توطئه های REG توجه کنیم این است که برخی از نقاط واقعاً دور از جایی که بیشتر نقاط متمرکز هستند وجود دارد ، ما قبلاً انتظار داشتیم که بعد از تفاوت بزرگ بین ستون های میانگین و STD ، چیزی شبیه به آن باشد – این نقاط ممکن است داده باشد موارد پرت و ارزش های افراطی.

یک مدل رگرسیون خطی ، یا uni یا چند متغیره ، هنگام تعیین شیب و ضرایب خط رگرسیون ، این مقادیر دورتر و شدید را در نظر می گیرد. با توجه به آنچه قبلاً از فرمول رگرسیون خطی می دانید:

$$
امتیاز = 9.68207815*ساعت+2.82689235
$$

اگر نقطه پرت 200 ساعت داشته باشیم، ممکن است یک خطای تایپی بوده باشد – همچنان برای محاسبه امتیاز نهایی استفاده می شود:

$$\begin{array}{c}سجorه=9.68207815\ast 200+2.82689235\\ سجorه=1939.24252235\end{array}$$

فقط یک نقطه پرت می تواند مقدار شیب ما را 200 برابر بزرگتر کند. همین امر برای رگرسیون خطی چندگانه نیز صادق است. فرمول رگرسیون خطی چندگانه اساساً بسط فرمول رگرسیون خطی با مقادیر شیب بیشتر است:

$$
y = b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n
$$

تفاوت اصلی بین این فرمول با فرمول قبلی ما، این است که آن را به عنوان توصیف می کند سطح، به جای توصیف یک خط. ما می دانیم که b_n * ایکس_n ضرایب به جای یک * x.

به همین ترتیب، اگر مقدار افراطی 17000 داشته باشیم، در نهایت شیب ما را 17000 بزرگتر می کند:

$$
y = b_0 + 17000 * x_1 + b_2 * x_2 + b_3 * x_3 + \ldots + b_n * x_n
$$

به عبارت دیگر مدل های خطی تک متغیره و چند متغیره هستند حساس به مقادیر پرت و داده های شدید.

اگر می‌خواهید درباره طرح‌های ویولن و طرح‌های جعبه‌ای اطلاعات بیشتری کسب کنید – راهنمای طرح جعبه و نقشه ویولن ما را بخوانید!

ما چیزهای زیادی در مورد مدل های خطی و تجزیه و تحلیل داده های اکتشافی یاد گرفته ایم، اکنون زمان استفاده از آن فرا رسیده است Average_income، Paved_Highways، Population_Driver_license(%) و Petrol_tax به عنوان متغیرهای مستقل مدل ما و ببینید چه اتفاقی می افتد.

آماده سازی داده ها

به دنبال آنچه با رگرسیون خطی ساده انجام شده است ، پس از بارگیری و کاوش در داده ها ، می توانیم آن را به ویژگی ها و اهداف تقسیم کنیم. تفاوت اصلی این است که اکنون ویژگی های ما به جای یک ستون، 4 ستون دارند.

می توانیم از دو براکت استفاده کنیم (( )) برای انتخاب آنها از چارچوب داده:

y = df('Petrol_Consumption')
X = df(('Average_income', 'Paved_Highways',
       'Population_Driver_licence(%)', 'Petrol_tax'))

پس از تنظیم ما X و y مجموعه ها، می توانیم داده های خود را به مجموعه های قطار و تست تقسیم کنیم. ما از همان دانه و 20 درصد داده های خود برای آموزش استفاده خواهیم کرد:

X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size=0.2, 
                                                    random_state=SEED)

آموزش مدل چند متغیره

پس از تقسیم داده ها، می توانیم مدل رگرسیون چندگانه خود را آموزش دهیم. توجه داشته باشید که اکنون نیازی به تغییر شکل ما نیست X داده، زمانی که از قبل بیش از یک بعد داشته باشد:

X.shape 

برای آموزش مدل خود می توانیم همان کد قبلی را اجرا کنیم و از آن استفاده کنیم fit() روش از LinearRegression کلاس:

regressor = LinearRegression()
regressor.fit(X_train, y_train)

پس از برازش مدل و یافتن راه‌حل بهینه، می‌توانیم به رهگیری نیز نگاه کنیم:

regressor.intercept_

361.45087906668397

و در ضرایب ویژگی ها

regressor.coef_

(-5.65355145e-02, -4.38217137e-03,  1.34686930e+03, -3.69937459e+01)

این چهار مقدار ضرایب هر یک از ویژگی های ما به همان ترتیبی هستند که آنها را در خود داریم X داده ها. برای دیدن لیستی با نام آنها می توانیم از dataframe استفاده کنیم columns صفت:

feature_names = X.columns

آن کد خروجی خواهد داشت:

('Average_income', 'Paved_Highways', 'Population_Driver_licence(%)', 'Petrol_tax')

با توجه به اینکه دیدن هر دو ویژگی و ضرایب با هم به این صورت کمی سخت است، بهتر می توانیم آنها را در قالب جدول سازماندهی کنیم.

برای انجام این کار، می توانیم نام ستون های خود را به a اختصاص دهیم feature_names متغیر، و ضرایب ما به a model_coefficients متغیر. پس از آن، می‌توانیم یک دیتافریم با ویژگی‌هایمان به‌عنوان شاخص و ضرایب خود به‌عنوان مقادیر ستون ایجاد کنیم. coefficients_df:

feature_names = X.columns
model_coefficients = regressor.coef_

coefficients_df = pd.DataFrame(data = model_coefficients, 
                              index = feature_names, 
                              columns = ('Coefficient value'))
print(coefficients_df)

آخرین DataFrame باید شبیه این باشد:

                              Coefficient value
Average_income                        -0.056536
Paved_Highways                        -0.004382
Population_Driver_licence(%)        1346.869298
Petrol_tax                           -36.993746

اگر در مدل رگرسیون خطی ، ما 1 متغیر و 1 ضریب داشتیم ، اکنون در مدل رگرسیون خطی چندگانه ، 4 متغیر و 4 ضرایب داریم. معنی آن ضرایب چیست؟ به دنبال همان تفسیر از ضرایب رگرسیون خطی ، این بدان معنی است که برای افزایش واحد در درآمد متوسط ​​، کاهش 0.06 دلار در مصرف گاز وجود دارد.

به طور مشابه، برای افزایش واحد در بزرگراه های آسفالت شده، 0.004 کاهش در مایل مصرف گاز وجود دارد. و برای افزایش واحد در نسبت جمعیت با گواهینامه رانندگی ، افزایش 1،346 میلیارد گالن مصرف گاز وجود دارد.

و در نهایت، برای افزایش واحد مالیات بر بنزین، کاهش 36993 میلیون گالن در مصرف گاز وجود دارد.

با نگاهی به چارچوب داده ضرایب، همچنین می‌توانیم ببینیم که طبق مدل ما، Average_income و Paved_Highways ویژگی‌ها آنهایی هستند که نزدیک‌تر به 0 هستند، به این معنی که آنها این ویژگی را دارند کمترین تاثیر روی مصرف گاز در حالی که Population_Driver_license(%) و Petrol_tax، با ضرایب 1346.86 و 36.99- به ترتیب دارای بزرگترین تاثیر روی پیش بینی هدف ما

به عبارت دیگر مصرف گاز بیشتر است توضیح داد با درصد جمعیت دارای گواهینامه رانندگی و میزان مالیات بر بنزین، به طور شگفت انگیزی (یا غیرقابل تعجب) به اندازه کافی.

ما می توانیم ببینیم که چگونه این نتیجه با آنچه در نقشه حرارتی همبستگی دیده بودیم ارتباط دارد. درصد گواهینامه رانندگی قوی ترین همبستگی داشت ، بنابراین انتظار می رفت که می تواند به توضیح مصرف گاز کمک کند ، و مالیات بنزین همبستگی منفی ضعیفی داشت – اما در مقایسه با متوسط ​​درآمد که همبستگی منفی ضعیف داشت – این بود همبستگی منفی که نزدیکترین به -1 بود و در نهایت مدل را توضیح داد.

هنگامی که تمام مقادیر به فرمول رگرسیون چندگانه اضافه شد ، بزرگراه های آسفالت شده و دامنه های متوسط ​​درآمد به 0 نزدیک شدند ، در حالی که درصد گواهینامه رانندگی و درآمد مالیاتی از 0 بیشتر شد. بنابراین این متغیرها وقتی بیشتر مورد توجه قرار گرفتند. پیدا کردن بهترین خط مناسب

به نظر می رسد تحلیل ما تا اینجا منطقی است. اکنون زمان آن است که مشخص کنیم آیا مدل فعلی ما مستعد خطا است یا خیر.

پیش بینی با مدل رگرسیون چند متغیره

برای درک اینکه آیا و چگونه مدل ما اشتباه می کند ، می توانیم مصرف گاز را با استفاده از داده های آزمون خود پیش بینی کنیم و سپس به معیارهای خود نگاه کنیم تا بتوانیم بگوییم مدل ما چقدر خوب رفتار می کند.

به همان روشی که برای مدل رگرسیون ساده انجام داده بودیم، بیایید با داده های آزمون پیش بینی کنیم:

y_pred = regressor.predict(X_test)

اکنون که پیش‌بینی‌های آزمایشی خود را داریم، بهتر می‌توانیم آنها را با مقادیر خروجی واقعی مقایسه کنیم X_test با سازماندهی آنها در یک DataFrameقالب:

results = pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})
print(results)

خروجی باید به شکل زیر باشد:

    Actual   Predicted
27     631  606.692665
40     587  673.779442
26     577  584.991490
43     591  563.536910
24     460  519.058672
37     704  643.461003
12     525  572.897614
19     640  687.077036
4      410  547.609366
25     566  530.037630

در اینجا، ما شاخص سطر هر داده تست، یک ستون برای مقدار واقعی آن و دیگری برای مقادیر پیش بینی شده آن داریم. وقتی به تفاوت بین مقادیر واقعی و پیش بینی شده ، مانند بین 631 تا 607 ، که 24 است ، یا بین 587 تا 674 نگاه می کنیم ، به نظر می رسد که بین هر دو مقدار فاصله ای وجود دارد ، اما این فاصله بیش از حد است ?

ارزیابی مدل چند متغیره

بعد از کاوش ، آموزش و نگاه به پیش بینی های مدل ما – مرحله نهایی ما ارزیابی عملکرد رگرسیون خطی چندگانه ما است. ما می‌خواهیم بفهمیم که آیا مقادیر پیش‌بینی‌شده ما از مقادیر واقعی ما خیلی دور است یا خیر. ما این کار را به همان روشی که قبلا انجام داده بودیم، با محاسبه معیارهای MAE، MSE و RMSE انجام خواهیم داد.

بنابراین، بیایید کد زیر را اجرا کنیم:

mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)

print(f'Mean absolute error: {mae:.2f}')
print(f'Mean squared error: {mse:.2f}')
print(f'Root mean squared error: {rmse:.2f}')

خروجی معیارهای ما باید این باشد:

Mean absolute error: 53.47
Mean squared error: 4083.26
Root mean squared error: 63.90

می توانیم ببینیم که مقدار RMSE 63.90 است ، به این معنی که مدل ما ممکن است با اضافه کردن یا کم کردن 63.90 از مقدار واقعی پیش بینی خود را اشتباه کند. بهتر است این خطا نزدیک به 0 باشد و 63.90 عدد بزرگی است – این نشان می دهد که مدل ما ممکن است خیلی خوب پیش بینی نکند.

MAE ما نیز از 0 فاصله دارد. در مقایسه با رگرسیون ساده قبلی ما که در آن نتیجه بهتری داشتیم ، می توانیم تفاوت معنی داری در بزرگی مشاهده کنیم.

برای حفر بیشتر آنچه در مدل ما اتفاق می افتد ، می توانیم به یک متریک نگاه کنیم که مدل را به روشی متفاوت اندازه گیری می کند ، مقادیر داده های فردی ما مانند MSE ، RMSE و MAE را در نظر نمی گیرد ، اما رویکرد کلی تری دارد خطا، R²:

$$
R^2 = 1 – \frac{\sum(واقعی – پیش بینی شده)^2}{\sum(واقعی – واقعی \ میانگین)^2}
$$

R² در مورد اینکه هر مقدار پیش بینی شده از داده های واقعی چقدر دور یا نزدیک است به ما نمی گوید – این به ما می گوید که چه مقدار از هدف ما توسط مدل ما گرفته می شود.

به عبارت دیگر، R² مقداری از واریانس متغیر وابسته توسط مدل توضیح داده شده است.

R² متریک از 0٪ تا 100٪ متغیر است. هر چه به 100% نزدیکتر باشد بهتر است. اگر R² مقدار منفی است، یعنی اصلاً هدف را توضیح نمی دهد.

می توانیم R را محاسبه کنیم² در پایتون برای درک بهتر روش کار:

actual_minus_predicted = sum((y_test - y_pred)**2)
actual_minus_actual_mean = sum((y_test - y_test.mean())**2)
r2 = 1 - actual_minus_predicted/actual_minus_actual_mean
print('R²:', r2)

R²: 0.39136640014305457

آر² همچنین به صورت پیش فرض در score روش کلاس رگرسیون خطی Scikit-Learn. ما می توانیم آن را به این صورت محاسبه کنیم:

regressor.score(X_test, y_test)

این منجر به:

0.39136640014305457

تا کنون ، به نظر می رسد که مدل فعلی ما فقط 39 ٪ از داده های آزمون ما را توضیح می دهد که نتیجه خوبی نیست ، به این معنی است که 61 ٪ از داده های آزمون را غیر قابل توضیح می گذارد.

بیایید همچنین درک کنیم که مدل ما تا چه اندازه داده های قطار ما را توضیح می دهد:

regressor.score(X_train, y_train)

کدام خروجی ها:

0.7068781342155135

ما یک مشکل در مدل خود پیدا کرده ایم. 70 درصد از داده‌های قطار را توضیح می‌دهد، اما تنها 39 درصد از داده‌های آزمایشی ما را توضیح می‌دهد که درست کردن آن از داده‌های قطار ما مهم‌تر است. این داده‌های قطار را به‌خوبی تطبیق می‌دهد، و نمی‌تواند با داده‌های آزمایشی مطابقت داشته باشد – به این معنی که ما داریم بیش از حد نصب شده مدل رگرسیون خطی چندگانه

عوامل زیادی ممکن است در این امر نقش داشته باشد که تعدادی از آنها می توانند عبارتند از:

1. نیاز به داده های بیشتر: ما فقط یک سال ارزش داده (و فقط 48 ردیف) داریم ، که چندان زیاد نیست ، در حالی که داشتن چندین سال داده می تواند به بهبود نتایج پیش بینی کمک کند.
2. غلبه بر بیش از حد: ما می توانیم از یک اعتبار سنجی متقاطع استفاده کنیم که مدل ما را با نمونه های مختلف تغییر یافته از مجموعه داده های ما متناسب کند تا سعی کنیم به پایان برسد.
3. مفروضاتی که صدق نمی کنند: ما فرض کرده ایم که داده ها رابطه خطی دارند، اما ممکن است اینطور نباشد. تجسم داده ها با استفاده از نمودارهای جعبه، درک توزیع داده ها، درمان نقاط دورافتاده و عادی سازی آن ممکن است به این امر کمک کند.
4. ویژگی‌های ضعیف: ممکن است به ویژگی‌های دیگری یا بیشتر نیاز داشته باشیم که روابط قوی‌تری با ارزش‌هایی که در تلاش برای پیش‌بینی آن‌ها هستند، داشته باشند.

نتیجه

در این مقاله یکی از اساسی ترین الگوریتم های یادگیری ماشین یعنی رگرسیون خطی را بررسی کرده ایم. ما هر دو رگرسیون خطی ساده و رگرسیون خطی چندگانه را با کمک کتابخانه یادگیری ماشینی Scikit-Learn اجرا کردیم.