سرور مجازی NVMe

طرح ریزی تصادفی: تئوری و پیاده سازی در پایتون با Scikit-Learn

Pythonبرنامه نویسی

توسط مهران در دی ۱۹, ۱۴۰۲

سرفصلهای مطلب

زمان لازم برای مطالعه: 11 دقیقه

معرفی

این راهنما مقدمه‌ای عمیق برای تکنیک کاهش ابعاد بدون نظارت است که نامیده می‌شود پیش بینی های تصادفی. یک طرح ریزی تصادفی می تواند برای کاهش پیچیدگی و اندازه داده ها استفاده شود و داده ها را آسان تر کند process و تجسم کنید. همچنین یک تکنیک پیش پردازش برای آماده سازی ورودی به یک طبقه بندی کننده یا یک رگرسیون است.

طرح ریزی تصادفی به طور معمول برای داده های بسیار بعدی، که در آن تکنیک های دیگر مانند تجزیه و تحلیل اجزای اصلی (PCA) نمی تواند عدالت داده ها را انجام دهد.

در این راهنما، ما به جزئیات آن خواهیم پرداخت لم جانسون-لیندن اشتراوس، که پایه ریاضی پیش بینی های تصادفی را می گذارد. ما همچنین نشان خواهیم داد که چگونه با استفاده از کتابخانه Scikit-Learn Python Projection تصادفی را انجام دهیم و از آن برای تبدیل داده های ورودی به فضایی با ابعاد کمتر استفاده کنیم.

تئوری نظریه است و عمل عمل است. به عنوان یک تصویر عملی، ما آن را بارگذاری می کنیم مجموعه داده جلد اول رویترز، و طرح ریزی تصادفی گاوسی و طرح تصادفی پراکنده را روی آن اعمال کنید.

طرح تصادفی یک مجموعه داده چیست؟

به زبان ساده:

فرافکنی تصادفی یک روش است کاهش ابعاد و تجسم داده ها که پیچیدگی مجموعه داده های با ابعاد بالا را ساده می کند.

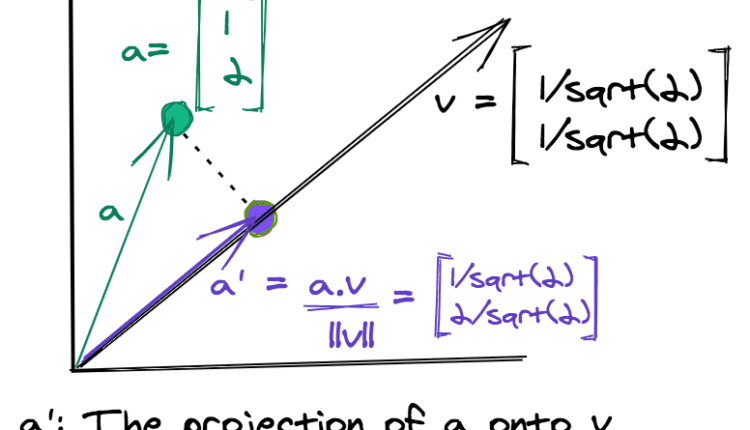
این روش با در نظر گرفتن طرح ریزی هر نقطه داده در امتداد مجموعه ای از جهت ها به طور تصادفی انتخاب شده، یک مجموعه داده جدید تولید می کند. طرح ریزی یک نقطه داده منفرد بر روی یک بردار از نظر ریاضی معادل گرفتن آن است حاصل ضرب نقطه با بردار.

با توجه به یک ماتریس داده $X$ با ابعاد $mxn$ و یک ماتریس $dxn$ $R$ که ستون های آن بردارهایی هستند که جهت های تصادفی را نشان می دهند، پیش بینی تصادفی $X$ با $X_p$.

${ایکس}_{پ} = ایکس آر$

هر بردار که یک جهت تصادفی را نشان می دهد دارای ابعاد $n$ است که مانند تمام نقاط داده $X$ است. اگر جهت‌های تصادفی $d$ را در نظر بگیریم، در نهایت به یک مجموعه داده تبدیل‌شده ابعادی $d$ می‌رسیم. برای هدف این آموزش، چند نماد را اصلاح می کنیم:

m: کل نقاط نمونه/نمونه های داده های ورودی.
n: مجموع ویژگی ها/ویژگی های داده های ورودی. همچنین ابعاد داده های اصلی است.
d: ابعاد داده های تبدیل شده.

ایده پیش بینی های تصادفی بسیار شبیه به تجزیه و تحلیل اجزای اصلی (PCA)، اساسا با این حال، در PCA، ماتریس طرح ریزی از طریق محاسبه می شود بردارهای ویژه، که می تواند از نظر محاسباتی برای ماتریس های بزرگ گران باشد.

هنگام انجام طرح ریزی تصادفی، بردارها به صورت تصادفی انتخاب می شوند و آن را بسیار کارآمد می کنند. نام “طرح بینی” ممکن است با انتخاب بردارها کمی گمراه کننده باشد به صورت تصادفی، نقاط تبدیل شده از نظر ریاضی پیش بینی های درست نیستند اما نزدیک به پیش بینی های واقعی هستند.

کار با داده هایی با ابعاد کاهش یافته آسان تر است. نه تنها می توان آن را تجسم کرد، بلکه می توان از آن در مرحله پیش پردازش نیز برای کاهش اندازه داده های اصلی استفاده کرد.

یک مثال ساده

فقط برای اینکه بفهمیم تبدیل چگونه کار می کند، مثال ساده زیر را در نظر می گیریم.

فرض کنید ماتریس ورودی ما $X$ توسط:

$ایکس = (\begin{matrix} 1 & 3 & 2 & 0 \\ 0 & 1 & 2 & 1 \\ 1 & 3 & 0 & 0 \end{matrix})$

و ماتریس طرح ریزی توسط:

$آر = \frac{1}{2} (\begin{matrix} 1 & - 1 \\ 1 & 1 \\ 1 & - 1 \\ 1 & 1 \end{matrix})$

طرح ریزی X بر روی R به صورت زیر است:

${ایکس}_{پ} = ایکس آر = \frac{1}{2} (\begin{matrix} 6 & 0 \\ 4 & 0 \\ 4 & 2 \end{matrix})$

ما با سه امتیاز در یک شروع کردیم فضای چهار بعدی، و با عملیات ماتریسی هوشمندانه به سه نقطه تبدیل شده در a ختم شد فضای دو بعدی.

به برخی از ویژگی های مهم ماتریس طرح ریزی $R$ توجه کنید. هر ستون یک ماتریس واحد است، یعنی هنجار هر ستون یک است. همچنین، حاصلضرب نقطه‌ای تمام ستون‌هایی که به‌صورت زوجی گرفته شده‌اند (در این مورد فقط ستون 1 و ستون 2) صفر است، که نشان می‌دهد هر دو بردار ستون متعامد با یکدیگر هستند.

این باعث می شود ماتریس، an ماتریس Orthonormal. با این حال، در مورد تکنیک طرح ریزی تصادفی، ماتریس طرح ریزی نباید یک ماتریس متعارف واقعی باشد زمانی که داده های با ابعاد بسیار بالا درگیر هستند.

موفقیت طرح ریزی تصادفی مبتنی است روی یک عالی یافته ریاضی معروف به جانسون-لینندندراس لیمما، که در قسمت زیر به تفصیل توضیح داده شده است!

لم جانسون-لیندن اشتراوس

لم جانسون-لیندن اشتراوس مبنای ریاضی برای طرح ریزی تصادفی است:

لم جانسون-لیندن اشتراوس بیان می کند که اگر نقاط داده در a قرار بگیرند فضای بسیار با ابعاد بالا، سپس چنین نکاتی را ارائه می دهد روی ساده جهت های تصادفی فاصله های زوجی خود را حفظ می کند.

حفظ مسافت های زوجی به این معنی است که فواصل زوجی بین نقاط در فضای اصلی یکسان یا تقریباً یکسان با فاصله زوجی در فضای کم‌بعد پیش‌بینی شده است.

بنابراین، ساختار داده‌ها و خوشه‌های درون داده‌ها در فضایی با ابعاد پایین‌تر نگهداری می‌شوند، در حالی که پیچیدگی و اندازه داده‌ها به طور قابل‌توجهی کاهش می‌یابد.

در این راهنما، ما به تفاوت فاصله‌های زوجی واقعی و پیش‌بینی‌شده به عنوان “اعوجاج” در داده ها که به دلیل طرح ریزی در فضای جدید معرفی شده است.

جانسون-لیندندروس لما نیز “بی خطر” اندازه گیری تعداد ابعاد برای نمایش نقاط داده بر روی آنها به طوری که خطا / اعوجاج در محدوده خاصی قرار دارد، بنابراین یافتن تعداد ابعاد مورد نظر آسان می شود.

از نظر ریاضی، با توجه به یک جفت نقطه $(x_1,x_2)$ و پیش بینی های مربوط به آنها $(x_1′,x_2′)$ یک eps-embedding:

$$
(1 – \epsilon) |x_1 – x_2|^2 < |x_1' - x_2'|^2 < (1 + \epsilon) |x_1 - x_2|^2
$$

لم جانسون-لیندنشتراوس حداقل ابعاد فضای کم بعدی را مشخص می کند به طوری که موارد فوق eps-embedding نگهداری می شود.

تعیین جهات تصادفی ماتریس پروجکشن

دو روش شناخته شده برای تعیین ماتریس طرح ریزی عبارتند از:

پیش بینی تصادفی گاوسی: ماتریس طرح ریزی با انتخاب عناصر به طور تصادفی از توزیع گاوسی با میانگین صفر ساخته می شود.
طرح ریزی تصادفی پراکنده: این یک روش نسبتاً ساده‌تر است، که در آن هر مؤلفه برداری مقداری از مجموعه {-k,0,+k} است که k یک ثابت است. یک طرح ساده برای تولید عناصر این ماتریس که به آن نیز می گویند Achlioptas روش تنظیم \ (k = \ sqrt 3 \) است:

${آر}_{من j} = \sqrt{3} {\begin{cases} + 1 & با احتمال & \frac{1}{6} \\ 0 & با احتمال & \frac{2}{3} \\ - 1 & با احتمال & \frac{1}{6} \end{cases}$

روش بالا معادل انتخاب اعداد از بین است {+k,0,-k} مستقر روی نتیجه انداختن یک تاس اگر امتیاز تاس باشد 1، سپس انتخاب کنید +k. اگر امتیاز تاس در محدوده باشد (2,5)، انتخاب کنید 0، و انتخاب کنید -k برای نمره تاس از 6.

یک روش کلی تر از a استفاده می کند density پارامتر برای انتخاب ماتریس طرح ریزی تصادفی. با تنظیم $s=\frac{1}{\text{density}}$، عناصر ماتریس Random Projection به صورت زیر انتخاب می شوند:

${آر}_{من j} = {\begin{cases} + \sqrt{\frac{س}{د}} & با احتمال & \frac{1}{2 س} \\ 0 & با احتمال & 1 - \frac{1}{س} \\ - \sqrt{\frac{س}{د}} & با احتمال & \frac{1}{2 س} \end{cases}$

توصیه کلی این است که تنظیم کنید density پارامتر به $\frac{1}{\sqrt n}$.

همانطور که قبلا ذکر شد، برای هر دو روش گاوسی و پراکنده، ماتریس طرح ریزی یک ماتریس متعامد واقعی نیست. با این حال، نشان داده شده است که در فضاهای با ابعاد بالا، ماتریس تصادفی انتخاب شده با استفاده از یکی از دو روش فوق نزدیک به یک ماتریس متعارف

طرح ریزی تصادفی با استفاده از Scikit-Learn

کتابخانه Scikit-Learn در اختیار ما قرار می دهد random_projection ماژول، که دارای سه کلاس / ماژول مهم است:

johnson_lindenstrauss_min_dim(): برای تعیین حداقل تعداد ابعاد داده های تبدیل شده هنگام داده شدن حجم نمونه m.
GaussianRandomProjection: پیش بینی های تصادفی گاوسی را انجام می دهد.
SparseRandomProjection: پیش بینی های تصادفی پراکنده را انجام می دهد.

ما هر سه مورد فوق را در بخش های زیر نشان خواهیم داد، اما ابتدا اجازه دهید import کلاس ها و توابعی که استفاده خواهیم کرد:

from sklearn.random_projection import SparseRandomProjection, johnson_lindenstrauss_min_dim
from sklearn.random_projection import GaussianRandomProjection
import numpy as np
from matplotlib import pyplot as plt
import sklearn.datasets as dt
from sklearn.metrics.pairwise import euclidean_distances

تعیین حداقل تعداد ابعاد از طریق لم جانسون لیندن اشتراوس

را johnson_lindenstrauss_min_dim() تابع حداقل تعداد ابعاد را تعیین می کند d، که با توجه به تعداد نمونه، می توان داده های ورودی را به آن نگاشت m، و eps یا پارامتر $\epsilon$.

کد زیر با تعداد متفاوتی از نمونه‌ها آزمایش می‌کند تا حداقل اندازه فضای کم‌بعد را تعیین کند، که یک مقدار مشخص را حفظ می‌کند. “بی خطر” تحریف داده ها

علاوه بر این، آن را ترسیم می کند log(d) در برابر مقادیر مختلف eps برای اندازه های مختلف نمونه m.

نکته مهمی که باید به آن توجه داشت این است که لم جانسون لیندن اشتراوس اندازه فضای کم‌بعد $d$ را فقط بر اساس تعیین می‌کند. روی تعداد نقاط مثال $m$ در داده های ورودی. تعداد ویژگی‌ها یا ویژگی‌های $n$ داده اصلی نامربوط است:

eps = np.arange(0.001, 0.999, 0.01)
colors = ('b', 'g', 'm', 'c')
m = (1e1, 1e3, 1e7, 1e10)
for i in range(4):
    min_dim = johnson_lindenstrauss_min_dim(n_samples=m(i), eps=eps)
    label = 'Total samples = ' + str(m(i))
    plt.plot(eps, np.log10(min_dim), c=colors(i), label=label)
    
plt.xlabel('eps')
plt.ylabel('log$_{10}$(d)')
plt.axhline(y=3.5, color='k', linestyle=':')
plt.legend()
plt.show()

از نمودار بالا، می توانیم ببینیم که برای مقادیر کوچک از eps، d بسیار بزرگ است اما کاهش می یابد eps به یکی نزدیک می شود. ابعاد زیر 3500 (خط سیاه نقطه چین) برای مقادیر متوسط تا بزرگ است eps.

این نشان می دهد که درخواست پیش بینی های تصادفی فقط معنی داره داده های با ابعاد بالا، از مرتبه هزاران ویژگی. در چنین مواردی می توان به کاهش زیادی در ابعاد دست یافت.

بنابراین، پیش‌بینی‌های تصادفی برای داده‌های متن یا تصویر، که شامل تعداد زیادی ویژگی ورودی است، بسیار موفق هستند، جایی که تجزیه و تحلیل مؤلفه اصلی می‌تواند

تبدیل داده ها

پایتون شامل اجرای پیش‌بینی‌های تصادفی گاوسی و پیش‌بینی‌های تصادفی پراکنده در خود می‌شود. sklearn کتابخانه از طریق دو کلاس GaussianRandomProjection و SparseRandomProjection به ترتیب. برخی از ویژگی های مهم برای این کلاس ها عبارتند از (لیست کامل نیست):

n_components: تعداد ابعاد داده های تبدیل شده. اگر تنظیم شده باشد auto، سپس ابعاد بهینه قبل از طرح ریزی تعیین می شود
eps: پارامتر لم جانسون-لیندن اشتراوس، که تعداد ابعاد را کنترل می کند به طوری که اعوجاج در داده های پیش بینی شده در یک محدوده مشخص نگه داشته می شود.
density: فقط برای SparseRandomProjection. مقدار پیش فرض است auto، که $s=\frac{1}{\sqrt n}$ را برای انتخاب ماتریس طرح ریزی تنظیم می کند.

مانند سایر کلاس های کاهش ابعاد sklearn، هر دو این کلاس ها شامل استاندارد هستند fit() و fit_transform() مواد و روش ها. مجموعه ای از ویژگی های قابل توجه که مفید هستند عبارتند از:

n_components: تعداد ابعاد فضای جدید روی که داده ها پیش بینی می شود.
components_: ماتریس تبدیل یا طرح ریزی.
density_: فقط برای SparseRandomProjection. ارزش آن است density مستقر روی که عناصر ماتریس طرح ریزی محاسبه می شوند.

طرح ریزی تصادفی با پروجکشن تصادفی گاوسی

بیایید با GaussianRandomProjection کلاس مقادیر ماتریس طرح ریزی به صورت هیستوگرام رسم می شوند و می بینیم که از توزیع گاوسی با میانگین صفر پیروی می کنند. اندازه ماتریس داده از 5000 به 3947 کاهش می یابد:

X_rand = np.random.RandomState(0).rand(100, 5000)
proj_gauss = GaussianRandomProjection(random_state=0)
X_transformed = proj_gauss.fit_transform(X_rand)


print('Shape of transformed data: ' + str(X_transformed.shape))


plt.hist(proj_gauss.components_.flatten())
plt.title('Histogram of the flattened transformation matrix')
plt.show()

این کد نتیجه می دهد:

Shape of transformed data: (100, 3947)

طرح ریزی تصادفی با SparseRandomProjection

کد زیر نشان می دهد که چگونه می توان با استفاده از یک طرح ریزی تصادفی پراکنده تبدیل داده ها را انجام داد. کل ماتریس تبدیل از سه مقدار مجزا تشکیل شده است که نمودار فرکانس آنها نیز در زیر نشان داده شده است.

توجه داشته باشید که ماتریس تبدیل a است SciPy پراکنده csr_matrix. کد زیر به مقادیر غیر صفر the دسترسی دارد csr_matrix و آنها را در آن ذخیره می کند p. بعد، استفاده می کند p برای به دست آوردن تعداد عناصر ماتریس طرح ریزی پراکنده:

proj_sparse = SparseRandomProjection(random_state=0)
X_transformed = proj_sparse.fit_transform(X_rand)


print('Shape of transformed data: ' + str(X_transformed.shape))




p = proj_sparse.components_.data
total_elements = proj_sparse.components_.shape(0) *\
                  proj_sparse.components_.shape(1)
pos = p(p>0)(0)
neg = p(p<0)(0)
print('Shape of transformation matrix: '+ str(proj_sparse.components_.shape))
counts = (sum(p==neg), total_elements - len(p), sum(p==pos))

plt.bar((neg, 0, pos), counts, width=0.1)
plt.xticks((neg, 0, pos))
plt.suptitle('Histogram of flattened transformation matrix, ' + 
             'density = ' +
             '{:.2f}'.format(proj_sparse.density_))
plt.show()

این نتیجه در:

Shape of transformed data: (100, 3947)
Shape of transformation matrix: (3947, 5000)

هیستوگرام مطابق با روش تولید یک ماتریس پراکنده تصادفی پراکنده است که در بخش قبل مورد بحث قرار گرفت. صفر با احتمال (1-1/100 = 0.99) انتخاب می شود، بنابراین حدود 99٪ مقادیر این ماتریس صفر است. استفاده از ساختارهای داده و روال برای ماتریس های پراکنده، این روش تبدیل را بسیار سریع و کارآمد می کند. روی مجموعه داده های بزرگ

پیش بینی های تصادفی عملی با مجموعه داده جلد 1 هسته رویترز

این بخش پیش بینی های تصادفی را نشان می دهد روی را مجموعه داده جلد اول رویترز. مجموعه داده به صورت آنلاین به صورت رایگان قابل دسترسی است، اگرچه برای اهداف ما، بارگیری از طریق Scikit-Learn آسان‌ترین کار است.

را sklearn.datasets ماژول شامل a fetch_rcv1() تابعی که مجموعه داده را دانلود و وارد می کند.

توجه داشته باشید: دانلود مجموعه داده ممکن است چند دقیقه طول بکشد، اگر هرگز آن را از قبل از طریق این روش وارد نکرده باشید. از آنجایی که نوار پیشرفت وجود ندارد، ممکن است به نظر برسد که اسکریپت بدون پیشرفت بیشتر در حال آویزان است. زمانی که در ابتدا آن را اجرا می کنید، کمی به آن زمان بدهید.

مجموعه داده RCV1 یک مجموعه داده چند برچسبی است، به عنوان مثال، هر نقطه داده می تواند به چندین کلاس به طور همزمان تعلق داشته باشد و از 103 کلاس تشکیل شده است. هر نقطه داده دارای ابعاد a است فوق العاده 47236، آن را به یک مورد ایده آل برای اعمال پیش بینی های تصادفی سریع و ارزان تبدیل می کند.

برای نشان دادن اثربخشی پیش‌بینی‌های تصادفی، و ساده نگه داشتن کارها، 500 نقطه داده را انتخاب می‌کنیم که به حداقل یکی از سه کلاس اول تعلق دارند. را fetch_rcv1() تابع مجموعه داده را بازیابی می کند و یک شی را با داده ها و اهدافی که هر دو پراکنده هستند برمی گرداند CSR ماتریس از SciPy.

بیایید Corpus رویترز را واکشی کنیم و آن را برای تبدیل داده ها آماده کنیم:

total_points = 500

dat = dt.fetch_rcv1()

target_nz = dat.target.nonzero()


ind_class_123 = np.asarray(np.where((target_nz(1)==0) |\
                                    (target_nz(1)==1) |\
                                    (target_nz(1) == 2))).flatten()

np.random.seed(0)
ind_class_123 = np.random.choice(ind_class_123, total_points, 
                                 replace=False)


row_ind = target_nz(0)(ind_class_123)
X = dat.data(row_ind,:)
y = np.array(dat.target(row_ind,0:3).todense())

پس از آماده سازی داده ها، به تابعی نیاز داریم که تصویری از داده های پیش بینی شده ایجاد کند. برای داشتن ایده ای از کیفیت تبدیل، می توانیم سه ماتریس زیر را محاسبه کنیم:

dist_raw: ماتریس فواصل اقلیدسی زوجی نقاط داده واقعی.
dist_transform: ماتریس فواصل اقلیدسی زوجی نقاط داده تبدیل شده.
abs_diff: ماتریس تفاوت مطلق dist_raw و dist_actual

را abs_diff_dist ماتریس شاخص خوبی برای کیفیت تبدیل داده است. مقادیر نزدیک به صفر یا کوچک در این ماتریس نشان دهنده اعوجاج کم و تبدیل خوب است. ما می‌توانیم مستقیماً تصویری از این ماتریس را نمایش دهیم یا هیستوگرام مقادیر آن را برای ارزیابی بصری تبدیل ایجاد کنیم. همچنین می‌توانیم میانگین تمام مقادیر این ماتریس را محاسبه کنیم تا یک معیار کمی برای مقایسه بدست آوریم.

کارکرد create_visualization() سه پلات ایجاد می کند. نمودار اول یک نمودار پراکنده از نقاط پیش بینی شده در امتداد دو جهت تصادفی اول است. نمودار دوم تصویری از ماتریس تفاوت مطلق و سومی هیستوگرام مقادیر ماتریس تفاوت مطلق است:

def create_visualization(X_transform, y, abs_diff):
    fig,ax = plt.subplots(nrows=1, ncols=3, figsize=(20,7))

    plt.subplot(131)
    plt.scatter(X_transform(y(:,0)==1,0), X_transform(y(:,0)==1,1), c='r', alpha=0.4)
    plt.scatter(X_transform(y(:,1)==1,0), X_transform(y(:,1)==1,1), c='b', alpha=0.4)
    plt.scatter(X_transform(y(:,2)==1,0), X_transform(y(:,2)==1,1), c='g', alpha=0.4)
    plt.legend(('Class 1', 'Class 2', 'Class 3'))
    plt.title('Projected data along first two dimensions')

    plt.subplot(132)
    plt.imshow(abs_diff)
    plt.colorbar()
    plt.title('Visualization of absolute differences')

    plt.subplot(133)
    ax = plt.hist(abs_diff.flatten())
    plt.title('Histogram of absolute differences')

    fig.subplots_adjust(wspace=.3)

مجموعه داده رویترز: طرح تصادفی گاوسی

بیایید پیش‌بینی تصادفی گاوسی را در مجموعه داده رویترز اعمال کنیم. کد زیر a اجرا می شود for حلقه برای مختلف eps ارزش های. اگر حداقل ابعاد ایمن توسط johnson_lindenstrauss_min_dim کمتر از ابعاد داده واقعی است، سپس آن را فراخوانی می کند fit_transform() روش از GaussianRandomProjection. را create_visualization() سپس تابع برای ایجاد تصویرسازی برای آن مقدار فراخوانی می شود eps.

در هر تکرار، کد همچنین میانگین اختلاف مطلق و درصد کاهش ابعاد به دست آمده توسط طرح تصادفی گاوسی را ذخیره می کند:

reduction_dim_gauss = ()
eps_arr_gauss = ()
mean_abs_diff_gauss = ()
for eps in np.arange(0.1, 0.999, 0.2):

    min_dim = johnson_lindenstrauss_min_dim(n_samples=total_points, eps=eps)
    if min_dim > X.shape(1):
        continue
    gauss_proj = GaussianRandomProjection(random_state=0, eps=eps)
    X_transform = gauss_proj.fit_transform(X)
    dist_raw = euclidean_distances(X)
    dist_transform = euclidean_distances(X_transform)
    abs_diff_gauss = abs(dist_raw - dist_transform) 

    create_visualization(X_transform, y, abs_diff_gauss)
    plt.suptitle('eps = ' + '{:.2f}'.format(eps) + ', n_components = ' + str(X_transform.shape(1)))
    
    reduction_dim_gauss.append(100-X_transform.shape(1)/X.shape(1)*100)
    eps_arr_gauss.append(eps)
    mean_abs_diff_gauss.append(np.mean(abs_diff_gauss.flatten()))

تصاویر ماتریس تفاوت مطلق و هیستوگرام مربوط به آن نشان می دهد که اکثر مقادیر نزدیک به صفر هستند. از این رو، اکثریت بزرگی از جفت نقاط فاصله واقعی خود را در فضای کم ابعاد حفظ می کنند و ساختار اصلی داده ها را حفظ می کنند.

برای ارزیابی کیفیت دگرگونی، بیایید میانگین تفاوت مطلق را در مقابل رسم کنیم eps. همچنین، هر چه ارزش بالاتر باشد eps، کاهش ابعاد بیشتر است. بیایید درصد کاهش در مقابل را نیز رسم کنیم. eps در طرح فرعی دوم:

fig,ax = plt.subplots(nrows=1, ncols=2, figsize=(10,5))
plt.subplot(121)
plt.plot(eps_arr_gauss, mean_abs_diff_gauss, marker='o', c='g')
plt.xlabel('eps')
plt.ylabel('Mean absolute difference')

plt.subplot(122)
plt.plot(eps_arr_gauss, reduction_dim_gauss, marker = 'o', c='m')
plt.xlabel('eps')
plt.ylabel('Percentage reduction in dimensionality')

fig.subplots_adjust(wspace=.4) 
plt.suptitle('Assessing the Quality of Gaussian Random Projections')
plt.show()

می بینیم که با استفاده از طرح تصادفی گاوسی می توانیم ابعاد داده ها را کاهش دهیم بیش از 99%! اگرچه، این میکند به قیمت تحریف بیشتر داده ها تمام می شود.

مجموعه داده رویترز: طرح ریزی تصادفی پراکنده

ما می توانیم مقایسه مشابهی را با طرح ریزی تصادفی پراکنده انجام دهیم:

reduction_dim_sparse = ()
eps_arr_sparse = ()
mean_abs_diff_sparse = ()
for eps in np.arange(0.1, 0.999, 0.2):

    min_dim = johnson_lindenstrauss_min_dim(n_samples=total_points, eps=eps)
    if min_dim > X.shape(1):
        continue
    sparse_proj = SparseRandomProjection(random_state=0, eps=eps, dense_output=1)
    X_transform = sparse_proj.fit_transform(X)
    dist_raw = euclidean_distances(X)
    dist_transform = euclidean_distances(X_transform)
    abs_diff_sparse = abs(dist_raw - dist_transform) 

    create_visualization(X_transform, y, abs_diff_sparse)
    plt.suptitle('eps = ' + '{:.2f}'.format(eps) + ', n_components = ' + str(X_transform.shape(1)))
    
    reduction_dim_sparse.append(100-X_transform.shape(1)/X.shape(1)*100)
    eps_arr_sparse.append(eps)
    mean_abs_diff_sparse.append(np.mean(abs_diff_sparse.flatten()))

در مورد پروجکشن تصادفی، ماتریس تفاوت مطلق شبیه به طرح ریزی گاوسی به نظر می رسد. داده های پیش بینی شده روی با این حال، دو بعد اول دارای الگوی جالب تری است که نقاط زیادی در آن ترسیم شده است روی محور مختصات

همچنین بیایید میانگین اختلاف مطلق و درصد کاهش ابعاد را برای مقادیر مختلف نشان دهیم eps پارامتر:

fig,ax = plt.subplots(nrows=1, ncols=2, figsize=(10,5))
plt.subplot(121)
plt.plot(eps_arr_sparse, mean_abs_diff_sparse, marker='o', c='g')
plt.xlabel('eps')
plt.ylabel('Mean absolute difference')

plt.subplot(122)
plt.plot(eps_arr_sparse, reduction_dim_sparse, marker = 'o', c='m')
plt.xlabel('eps')
plt.ylabel('Percentage reduction in dimensionality')

fig.subplots_adjust(wspace=.4) 
plt.suptitle('Assessing the Quality of Sparse Random Projections')
plt.show()

روند دو نمودار مشابه روند یک طرح گاوسی است. با این حال، میانگین تفاوت مطلق برای طرح گاوسی کمتر از پیش بینی تصادفی است.

نتیجه گیری

در این راهنما، جزئیات دو نوع اصلی پیش‌بینی تصادفی، یعنی پیش‌بینی تصادفی گاوسی و پراکنده را مورد بحث قرار دادیم.

ما جزئیات را ارائه کردیم لم جانسون-لیندن اشتراوس، مبنای ریاضی این روش ها است. سپس نشان دادیم که چگونه می توان از این روش برای تبدیل داده ها با استفاده از پایتون استفاده کرد sklearn کتابخانه

ما همچنین این دو روش را نشان دادیم روی یک زندگی واقعی مجموعه داده جلد اول رویترز.

ما خواننده را تشویق می‌کنیم که این روش را در طبقه‌بندی نظارت شده یا وظایف رگرسیون در مرحله پیش‌پردازش، زمانی که با مجموعه داده‌های بسیار بعدی سروکار دارد، امتحان کند.

(برچسب‌ها به ترجمه)# python

منتشر شده در 1403-01-09 00:02:02

امتیاز شما به این مطلب