نقشه های خودسازماندهی: تئوری و پیاده سازی در پایتون با NumPy

معرفی

در این راهنما، نگاهی به یک مدل یادگیری بدون نظارت، معروف به a نقشه خودسازماندهی (SOM)و همچنین پیاده سازی آن در پایتون. ما از یک استفاده خواهیم کرد رنگ RGB مثالی برای آموزش SOM و نشان دادن عملکرد و استفاده معمولی آن.

نقشه های خودسازماندهی: مقدمه ای کلی

آ نقشه خودسازماندهی اولین بار توسط Teuvo Kohonen در سال 1982 و گاهی اوقات به عنوان a نیز شناخته می شود نقشه کوهونن. این یک نوع خاص از an است شبکه های عصبی مصنوعی، که نقشه ای از داده های آموزشی می سازد. نقشه به طور کلی یک شبکه مستطیلی دوبعدی از وزن ها است اما می تواند به یک مدل سه بعدی یا ابعاد بالاتر گسترش یابد. ساختارهای شبکه ای دیگر مانند شبکه های شش ضلعی نیز امکان پذیر است.

SOM عمدتاً برای تجسم داده ها استفاده می شود و خلاصه تصویری سریعی از نمونه های آموزشی ارائه می دهد. در یک شبکه مستطیلی دو بعدی، هر سلول با یک بردار وزنی نمایش داده می شود. برای یک SOM آموزش دیده، وزن هر سلول خلاصه ای از چند نمونه تمرینی را نشان می دهد. سلول‌های نزدیک به هم وزن‌های مشابهی دارند و نمونه‌های مشابهی را می‌توان به سلول‌های همسایه کوچک یکدیگر نگاشت.

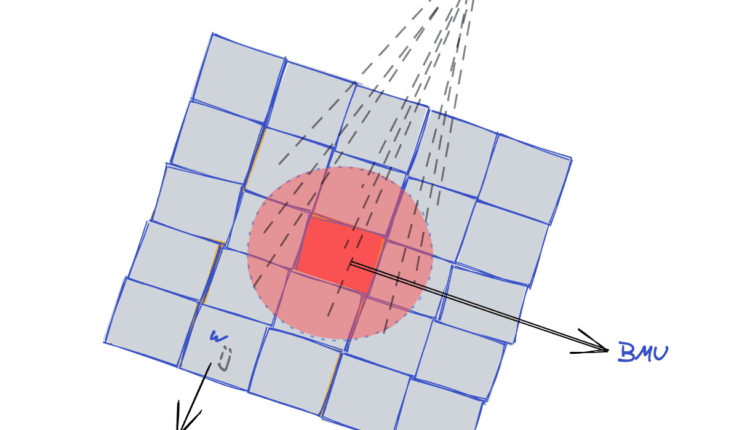
شکل زیر یک تصویر تقریبی از ساختار SOM است:

یک SOM با استفاده از آموزش دیده می شود یادگیری رقابتی.

یادگیری رقابتی شکلی از یادگیری بدون نظارت است که در آن عناصر تشکیل دهنده برای به دست آوردن یک نتیجه رضایت بخش با یکدیگر رقابت می کنند و تنها یکی می تواند برنده رقابت شود.

هنگامی که یک مثال آموزشی وارد شبکه می شود، بهترین واحد تطبیق (BMU) مشخص می شود (برنده مسابقه). BMU سلولی است که وزن آن به نمونه تمرینی نزدیکتر است.

سپس، وزن BMU و وزن سلول‌های همسایه BMU، برای نزدیک‌تر شدن به نمونه تمرین ورودی تنظیم می‌شوند. در حالی که انواع معتبر دیگری از آموزش SOM وجود دارد، ما محبوب ترین و پرکاربردترین پیاده سازی SOM را در این راهنما ارائه می دهیم.

از آنجایی که از برخی روال های پایتون برای نشان دادن توابع مورد استفاده برای آموزش SOM استفاده می کنیم، بیایید import تعدادی از کتابخانه هایی که استفاده خواهیم کرد:

import numpy as np
import matplotlib.pyplot as plt

الگوریتم پشت نقشه های خودسازماندهی آموزش

الگوریتم اصلی برای آموزش SOM در زیر آورده شده است:

• همه وزن های شبکه SOM را مقداردهی کنید
• این کار را تا رسیدن به همگرایی یا حداکثر دوره تکرار کنید
  • مثال های آموزشی را با هم مخلوط کنید
  • برای هر نمونه آموزشی \(x\)
    • بهترین واحد تطبیق BMU را پیدا کنید
    • بردار وزن BMU و سلول های مجاور آن را به روز کنید

سه مرحله برای مقداردهی اولیه، یافتن BMU و به روز رسانی وزن ها در بخش های زیر توضیح داده شده است. شروع کنیم!

راه اندازی شبکه SOM GRID

تمام وزن های شبکه SOM را می توان به طور تصادفی مقداردهی اولیه کرد. وزن‌های شبکه SOM همچنین می‌توانند با نمونه‌های انتخابی تصادفی از مجموعه داده آموزشی مقداردهی اولیه شوند.

کدام را باید انتخاب کنید؟

SOM ها به وزن اولیه نقشه حساس هستند، بنابراین این انتخاب بر مدل کلی تأثیر می گذارد. مطابق با یک مطالعه موردی اجرا شده توسط Ayodeji و Evgeny از دانشگاه لستر و دانشگاه فدرال سیبری:

با مقایسه نسبت نقشه نهایی SOM از RI (راه‌اندازی تصادفی) که عملکرد بهتری داشت PCI (Principal Component Initialization) تحت شرایط مشابه، مشاهده شد که RI برای مجموعه داده‌های غیرخطی کاملاً خوب عمل می‌کند.

با این حال، برای مجموعه داده های شبه خطی، نتیجه غیرقابل قطعیت است. به طور کلی، می‌توان نتیجه گرفت که فرضیه مزایای PCI برای مجموعه داده‌های اساساً غیرخطی اشتباه است.

مقداردهی اولیه تصادفی بهتر از مقداردهی اولیه غیر تصادفی برای مجموعه داده های غیرخطی است. برای مجموعه داده های شبه خطی، کاملاً مشخص نیست که کدام رویکرد به طور مداوم برنده است. با توجه به این نتایج – ما به آن پایبند خواهیم بود مقداردهی اولیه تصادفی.

یافتن بهترین واحد تطبیق (BMU)

همانطور که قبلا ذکر شد، بهترین واحد تطبیق، سلول شبکه SOM است که نزدیکترین به مثال آموزشی \(x\) است. یکی از روش های یافتن این واحد، محاسبه آن است فاصله اقلیدسی از \(x\) از وزن هر سلول شبکه.

سلول با حداقل فاصله را می توان به عنوان BMU انتخاب کرد.

نکته مهمی که باید به آن توجه داشت این است که فاصله اقلیدسی تنها روش ممکن برای انتخاب BMU نیست. یک اندازه‌گیری فاصله جایگزین یا یک متریک شباهت نیز می‌تواند برای تعیین BMU استفاده شود، و انتخاب آن عمدتاً بستگی دارد روی داده ها و مدلی که به طور خاص می سازید.

به روز رسانی بردار وزن BMU و سلول های همسایه

یک مثال آموزشی \(x\) سلول های مختلف شبکه SOM را با کشیدن وزنه های این سلول ها به سمت آن تحت تاثیر قرار می دهد. حداکثر تغییر در BMU رخ می دهد و با دور شدن از BMU در شبکه SOM، تأثیر \(x\) کاهش می یابد. برای سلولی با مختصات \((i,j)\)، وزن آن \(w_{ij}\) در دوره \(t+1\) به‌صورت زیر به‌روزرسانی می‌شود:

$$
w_{ij}^{(t+1)} \lefttarrow w_{ij}^{

جایی که \(\Delta w_{ij}^{

$$
\Delta w_{ij}^{

برای این عبارت:

• \(t\) عدد دوره است
• \((g,h)\) مختصات BMU هستند
• \(\eta\) نرخ یادگیری است
• \(\sigma_t\) شعاع است
• \(f_{ij}(g,h,\sigma_t)\) تابع فاصله همسایگی است

در بخش های بعدی، جزئیات این عبارت تمرینی با وزنه را ارائه خواهیم کرد.

میزان یادگیری

نرخ یادگیری \(\eta\) یک ثابت در محدوده (0,1) است و اندازه گام بردار وزن را به سمت مثال آموزشی ورودی تعیین می کند. برای \(\eta=0\)، تغییری در وزن وجود ندارد و وقتی \(\eta=1\) بردار وزن \(w_{ij}\) مقدار \(x\) را می گیرد.

\(\eta\) در ابتدا بالا نگه داشته می شود و با ادامه دوره ها تحلیل می رود. یک استراتژی برای کاهش نرخ یادگیری در مرحله آموزش استفاده از فروپاشی نمایی است:

$$
\eta^{

جایی که \(\lambda<0\) نرخ فروپاشی است.

برای درک اینکه چگونه نرخ یادگیری با نرخ فروپاشی تغییر می‌کند، بیایید نرخ یادگیری را بر اساس دوره‌های مختلف زمانی که نرخ یادگیری اولیه روی یک تنظیم می‌شود ترسیم کنیم:

epochs = np.arange(0, 50)
lr_decay = (0.001, 0.1, 0.5, 0.99)
fig,ax = plt.subplots(nrows=1, ncols=4, figsize=(15,4))
plt_ind = np.arange(4) + 141
for decay, ind in zip(lr_decay, plt_ind):
    plt.subplot(ind)
    learn_rate = np.exp(-epochs * decay)
    plt.plot(epochs, learn_rate, c='cyan')
    plt.title('decay rate: ' + str(decay))
    plt.xlabel('epochs $t$')
    plt.ylabel('$\eta^
fig.subplots_adjust(hspace=0.5, wspace=0.3)
plt.show()

تابع فاصله محله

تابع فاصله همسایگی توسط:

$$
f_{ij}(g,h,\sigma_t) = e^\frac{-d((i,j),(g,h))^2}{2\sigma_t^2}
$$

که در آن \(d((i,j),(g,h))\) فاصله مختصات \((i,j)\) یک سلول از مختصات BMU \((g,h)\) است. و \(\sigma_t\) شعاع در دوره \(t\) است. معمولاً فاصله اقلیدسی برای محاسبه فاصله استفاده می شود، با این حال، هر متریک فاصله یا تشابه دیگری را می توان استفاده کرد.

از آنجایی که فاصله BMU با خودش صفر است، تغییر وزن BMU به زیر کاهش می یابد:

$$
\Delta w_{gh} = \eta (x-w_{gh})
$$

برای یک واحد \((i,j)\) که فاصله زیادی از BMU دارد، تابع فاصله همسایگی به مقدار نزدیک به صفر کاهش می‌یابد که منجر به بزرگی بسیار کوچک \(\Delta w_{ij}\) می‌شود. بنابراین، چنین واحدهایی تحت تأثیر مثال آموزشی \(x\) قرار ندارند. بنابراین، یک مثال آموزشی، تنها بر BMU و سلول های نزدیک به BMU تاثیر می گذارد. همانطور که از BMU دور می شویم، تغییر وزن کمتر و کمتر می شود تا زمانی که ناچیز باشد.

شعاع ناحیه نفوذ یک مثال آموزشی \(x\) را تعیین می کند. یک مقدار شعاع بالا بر تعداد بیشتری از سلول ها تأثیر می گذارد و شعاع کوچکتر فقط بر BMU تأثیر می گذارد. یک استراتژی رایج این است که با یک شعاع بزرگ شروع کنید و در طول دوره ها آن را کاهش دهید، به عنوان مثال:

$$
\sigma_t = \sigma_0 e^{-t*\beta}
$$

در اینجا \(\beta<0\) میزان فروپاشی است. نرخ پوسیدگی مربوط به شعاع نیز همین اثر را دارد روی شعاع به عنوان نرخ فروپاشی مربوط به نرخ یادگیری است. برای به دست آوردن بینشی عمیق تر از رفتار تابع همسایگی، اجازه دهید آن را در برابر فاصله برای مقادیر مختلف شعاع رسم کنیم. نکته ای که در این نمودارها باید به آن توجه کرد این است که تابع فاصله به مقدار نزدیک به صفر نزدیک می شود زیرا فاصله از 10 برای \(\sigma^2 \leq 10\) بیشتر می شود.

ما بعداً از این واقعیت برای کارآمدتر کردن آموزش در بخش پیاده سازی استفاده خواهیم کرد:

distance = np.arange(0, 30)
sigma_sq = (0.1, 1, 10, 100)
fig,ax = plt.subplots(nrows=1, ncols=4, figsize=(15,4))
plt_ind = np.arange(4) + 141
for s, ind in zip(sigma_sq, plt_ind):
    plt.subplot(ind)
    f = np.exp(-distance ** 2 / 2 / s)
    plt.plot(distance, f, c='cyan')
    plt.title('$\sigma^2$ = ' + str(s))
    plt.xlabel('Distance')
    plt.ylabel('Neighborhood function $f$')
fig.subplots_adjust(hspace=0.5, wspace=0.3)
plt.show()

پیاده سازی نقشه خودسازماندهی در پایتون با استفاده از NumPy

از آنجایی که هیچ روال داخلی برای یک SOM در کتابخانه یادگیری ماشین استاندارد بالفعل وجود ندارد، Scikit-Learn، پیاده سازی سریع را به صورت دستی و با استفاده از آن انجام خواهیم داد NumPy. مدل یادگیری ماشینی بدون نظارت بسیار ساده و آسان برای پیاده سازی است.

ما SOM را به صورت دو بعدی پیاده سازی می کنیم mxn شبکه، از این رو به یک 3 بعدی نیاز دارد NumPy آرایه. بعد سوم برای ذخیره وزن ها در هر سلول مورد نیاز است:

def find_BMU(SOM,x):
    distSq = (np.square(SOM - x)).sum(axis=2)
    return np.unravel_index(np.argmin(distSq, axis=None), distSq.shape)
    


def update_weights(SOM, train_ex, learn_rate, radius_sq, 
                   BMU_coord, step=3):
    g, h = BMU_coord
    
    if radius_sq < 1e-3:
        SOM(g,h,:) += learn_rate * (train_ex - SOM(g,h,:))
        return SOM
    
    for i in range(max(0, g-step), min(SOM.shape(0), g+step)):
        for j in range(max(0, h-step), min(SOM.shape(1), h+step)):
            dist_sq = np.square(i - g) + np.square(j - h)
            dist_func = np.exp(-dist_sq / 2 / radius_sq)
            SOM(i,j,:) += learn_rate * dist_func * (train_ex - SOM(i,j,:))   
    return SOM    



def train_SOM(SOM, train_data, learn_rate = .1, radius_sq = 1, 
             lr_decay = .1, radius_decay = .1, epochs = 10):    
    learn_rate_0 = learn_rate
    radius_0 = radius_sq
    for epoch in np.arange(0, epochs):
        rand.shuffle(train_data)      
        for train_ex in train_data:
            g, h = find_BMU(SOM, train_ex)
            SOM = update_weights(SOM, train_ex, 
                                 learn_rate, radius_sq, (g,h))
        
        learn_rate = learn_rate_0 * np.exp(-epoch * lr_decay)
        radius_sq = radius_0 * np.exp(-epoch * radius_decay)            
    return SOM

بیایید توابع کلیدی مورد استفاده برای اجرای یک نقشه خودسازماندهی را تجزیه کنیم:

find_BMU() مختصات سلول شبکه بهترین واحد منطبق را در صورت داده شدن برمی گرداند SOM شبکه و یک مثال آموزشی x. مجذور فاصله اقلیدسی بین وزن هر سلول و x، و برمی گردد (g,h)، یعنی سلول با حداقل فاصله مختصات می شود.

را update_weights() تابع نیاز به یک شبکه SOM، یک مثال آموزشی دارد x، پارامترها learn_rate و radius_sq، مختصات بهترین واحد تطبیق، و الف step پارامتر. از نظر تئوری، تمام سلول های SOM به روز می شوند روی نمونه آموزشی بعدی با این حال، ما قبلا نشان دادیم که این تغییر برای سلول هایی که از BMU دور هستند ناچیز است. از این رو، می‌توانیم کد را با تغییر تنها سلول‌های موجود در مجاورت کوچک BMU کارآمدتر کنیم. را step پارامتر حداکثر تعداد سلول ها را مشخص می کند روی چپ، راست، بالا و پایین برای تغییر هنگام به‌روزرسانی وزنه‌ها.

در نهایت، train_SOM() تابع روش اصلی آموزش یک SOM را پیاده سازی می کند. این نیاز به یک مقدار اولیه یا تا حدی آموزش دیده دارد SOM شبکه و train_data به عنوان پارامتر مزیت این است که بتوانیم SOM را از مرحله آموزش قبلی آموزش دهیم. علاوه بر این learn_rate و radius_sq پارامترها همراه با نرخ پوسیدگی مربوطه مورد نیاز هستند lr_decay و radius_decay. را epochs پارامتر به طور پیش فرض روی 10 تنظیم شده است اما در صورت نیاز می توان آن را تغییر داد.

اجرای نقشه خودسازماندهی روی یک مثال عملی

یکی از مثال‌های رایج برای آموزش SOM، رنگ‌های تصادفی است. ما می توانیم یک شبکه SOM را آموزش دهیم و به راحتی تجسم کنیم که چگونه رنگ های مشابه مختلف در سلول های همسایه چیده می شوند.

سلول های دور از یکدیگر رنگ های متفاوتی دارند.

بیایید اجرا کنیم train_SOM() تابع روی یک ماتریس داده آموزشی پر از رنگ های تصادفی RGB.

کد زیر یک ماتریس داده آموزشی و یک شبکه SOM با رنگ های تصادفی RGB را مقداردهی اولیه می کند. همچنین داده های آموزشی و مقدار دهی اولیه را به صورت تصادفی نمایش می دهد شبکه SOM. توجه داشته باشید، ماتریس آموزشی یک ماتریس 3000×3 است، اما برای تجسم آن را به ماتریس 50x60x3 تغییر شکل داده ایم:

m = 10
n = 10

n_x = 3000
rand = np.random.RandomState(0)

train_data = rand.randint(0, 255, (n_x, 3))

SOM = rand.randint(0, 255, (m, n, 3)).astype(float)

fig, ax = plt.subplots(
    nrows=1, ncols=2, figsize=(12, 3.5), 
    subplot_kw=dict(xticks=(), yticks=()))
ax(0).imshow(train_data.reshape(50, 60, 3))
ax(0).title.set_text('Training Data')
ax(1).imshow(SOM.astype(int))
ax(1).title.set_text('Randomly Initialized SOM Grid')

بیایید اکنون SOM را آموزش دهیم و بررسی کنیم روی هر 5 دوره به عنوان یک نمای کلی از پیشرفت آن:

fig, ax = plt.subplots(
    nrows=1, ncols=4, figsize=(15, 3.5), 
    subplot_kw=dict(xticks=(), yticks=()))
total_epochs = 0
for epochs, i in zip((1, 4, 5, 10), range(0,4)):
    total_epochs += epochs
    SOM = train_SOM(SOM, train_data, epochs=epochs)
    ax(i).imshow(SOM.astype(int))
    ax(i).title.set_text('Epochs = ' + str(total_epochs))

مثال بالا بسیار جالب است زیرا نشان می دهد که چگونه شبکه به طور خودکار رنگ های RGB را مرتب می کند به طوری که سایه های مختلف یک رنگ در شبکه SOM به هم نزدیک می شوند. تنظیم در اوایل دوره اول اتفاق می افتد، اما ایده آل نیست. می بینیم که SOM در حدود 10 دوره همگرا می شود و تغییرات کمتری در دوره های بعدی وجود دارد.

تأثیر سرعت و شعاع یادگیری

برای اینکه ببینیم نرخ یادگیری برای سرعت‌ها و شعاع‌های مختلف یادگیری چگونه تغییر می‌کند، می‌توانیم SOM را برای 10 دوره زمانی که از همان شبکه اولیه شروع می‌کنیم، اجرا کنیم. کد زیر SOM را برای سه مقدار مختلف از نرخ یادگیری و سه شعاع مختلف آموزش می دهد.

SOM پس از 5 دوره برای هر شبیه سازی ارائه می شود:

fig, ax = plt.subplots(
    nrows=3, ncols=3, figsize=(15, 15), 
    subplot_kw=dict(xticks=(), yticks=()))



for learn_rate, i in zip((0.001, 0.5, 0.99), (0, 1, 2)):
    for radius_sq, j in zip((0.01, 1, 10), (0, 1, 2)):
        rand = np.random.RandomState(0)
        SOM = rand.randint(0, 255, (m, n, 3)).astype(float)        
        SOM = train_SOM(SOM, train_data, epochs = 5,
                        learn_rate = learn_rate, 
                        radius_sq = radius_sq)
        ax(i)(j).imshow(SOM.astype(int))
        ax(i)(j).title.set_text('$\eta$ = ' + str(learn_rate) + 
                                ', $\sigma^2$ = ' + str(radius_sq))
                                

مثال بالا نشان می دهد که برای مقادیر شعاع نزدیک به صفر (ستون اول)، SOM فقط سلول های جداگانه را تغییر می دهد اما سلول های مجاور را تغییر نمی دهد. از این رو، بدون توجه به میزان یادگیری، یک نقشه مناسب ایجاد نمی شود. مورد مشابهی نیز برای میزان یادگیری کوچکتر (ردیف اول، ستون دوم) مشاهده می شود. مانند هر الگوریتم یادگیری ماشین دیگری، تعادل خوبی از پارامترها برای آموزش ایده آل مورد نیاز است.

نتیجه گیری

در این راهنما، مدل نظری SOM و اجرای دقیق آن را مورد بحث قرار دادیم. ما SOM را نشان دادیم روی رنگ های RGB و نشان می دهد که چگونه سایه های مختلف یک رنگ خود را سازماندهی می کنند روی یک شبکه دو بعدی

در حالی که SOM ها دیگر در جامعه یادگیری ماشینی محبوب نیستند، اما مدل خوبی برای خلاصه سازی و تجسم داده ها هستند.