محاسبه ضریب همبستگی رتبه اسپیرمن در پایتون با پانداها

معرفی

این راهنما مقدمه ای است برای ضریب همبستگی رتبه اسپیرمن، محاسبه ریاضی آن و محاسبه آن از طریق پایتون pandas کتابخانه ما مثال‌های مختلفی می‌سازیم تا درک اساسی از این ضریب به دست آوریم و روش تجسم آن را نشان دهیم ماتریس همبستگی از طریق نقشه های حرارتی.

ضریب همبستگی رتبه اسپیرمن چیست؟

همبستگی رتبه اسپیرمن ارتباط نزدیکی با همبستگی پیرسون، و هر دو یک مقدار محدود هستند، از -1 به 1 نشان دهنده a همبستگی بین دو متغیر

اگر مایلید در مورد ضریب همبستگی جایگزین بیشتر بخوانید – راهنمای ما برای ضریب همبستگی پیرسون در پایتون را بخوانید.

ضریب همبستگی پیرسون با استفاده از مقادیر داده خام محاسبه می شود، در حالی که همبستگی اسپیرمن از رتبه ها از ارزش های فردی در حالی که ضریب همبستگی پیرسون معیاری از رابطه خطی بین دو متغیر است، ضریب همبستگی رتبه اسپیرمن رابطه یکنواخت بین یک متغیر را اندازه گیری می کند. جفت متغیر. برای درک همبستگی اسپیرمن، ما نیاز به درک اساسی داریم توابع یکنواخت.

توابع یکنواخت

توابع یکنواخت افزایشی، یکنواخت کاهشی و غیر یکنواخت وجود دارد.

برای یک تابع افزایش یکنواخت، با افزایش X، Y نیز افزایش می‌یابد (و لازم نیست خطی باشد). برای یک تابع نزولی یکنواخت، با افزایش یک متغیر، متغیر دیگر کاهش می یابد (همچنین لازم نیست خطی باشد). تابع غیر یکنواخت جایی است که افزایش مقدار یک متغیر می تواند گاهی منجر به افزایش و گاهی به کاهش مقدار متغیر دیگر شود.

ضریب همبستگی رتبه اسپیرمن اندازه گیری می شود رابطه یکنواخت بین دو متغیر. مقادیر آن از -1 تا +1 متغیر است و می توان آن را به صورت زیر تفسیر کرد:

• +1: رابطه کاملاً یکنواخت در حال افزایش است
• +0.8: رابطه قوی یکنواخت در حال افزایش
• +0.2: رابطه ضعیف یکنواخت در حال افزایش
• 0: رابطه غیر یکنواخت
• -0.2: رابطه ضعیف یکنواخت در حال کاهش
• -0.8: رابطه قوی یکنواخت در حال کاهش
• -1: رابطه کاملاً یکنواخت در حال کاهش است

بیان ریاضی

فرض کنید که مشاهده \(n\) از دو متغیر تصادفی \(X\) و \(Y\) داریم. ابتدا تمام مقادیر هر دو متغیر را به ترتیب \(X_r\) و \(Y_r\) رتبه بندی می کنیم. ضریب همبستگی رتبه اسپیرمن با \(r_s\) نشان داده می شود و به صورت زیر محاسبه می شود:

$$
r_s = \rho_{X_r,Y_r} = \frac{\text{COV}(X_r,Y_r)}{\text{STD}(X_r)\text{STD}(Y_r)} = \frac{n\sum\ limits_{x_r\in X_r, y_r \in Y_r} x_r y_r – \sum\limits_{x_r\in X_r}x_r\sum\limits_{y_r\in Y_r}y_r}{\sqrt{\Big(n\sum\limits_ {x_r \in X_r} x_r^2 -(\sum\limits_{x_r\in X_r}x_r)^2\Big)}\sqrt{\Big(n\sum\limits_{y_r \in Y_r} y_r^2 – (\sum\limits_{y_r\in Y_r}y_r)^2 \Big)}}
$$

اینجا، COV() کوواریانس است و STD() انحراف معیار است. قبل از اینکه توابع پایتون را برای محاسبه این ضریب ببینیم، بیایید یک محاسبه مثالی با دست انجام دهیم تا این عبارت را بفهمیم و آن را درک کنیم.

محاسبات مثال

فرض کنید مشاهداتی از متغیرهای تصادفی \(X\) و \(Y\) به ما داده شده است. اولین مرحله تبدیل \(X\) و \(Y\) به \(X_r\) و \(Y_r\) است که نشان دهنده رتبه های مربوط به آنها است. چند مقدار میانی نیز مورد نیاز است که در زیر نشان داده شده است:

$$\begin{array}{lcccccccc}\mathrm{ایکس}& =& (& –2& –1& 0& 1& 2& {)}^{\mathrm{تی}}\\ Y& =& (& 4& 1& 3& 2& 0& {)}^{\mathrm{تی}}\\ {\mathrm{ایکس}}_r& =& (& 1& 2& 3& 4& 5& {)}^{\mathrm{تی}}\\ Y_r& =& (& 5& 2& 4& 3& 1& {)}^{\mathrm{تی}}\\ {\mathrm{ایکس}}_r^2& =& (& 1& 4& 9& 16& 25& {)}^{\mathrm{تی}}\\ Y_r^2& =& (& 25& 4& 16& 9& 1& {)}^{\mathrm{تی}}\\ {\mathrm{ایکس}}_r{Y}_r& =& (& 5& 4& 12& 12& 5& {)}^{\mathrm{تی}}\end{array}$$

بیایید از فرمول قبلی برای محاسبه همبستگی اسپیرمن استفاده کنیم:

$$r_{س}=\frac{5\ast 38–(15)(15)}{\sqrt{(5\ast 55–{15}^2)}\sqrt{(5\ast 55–{15}^2)}}=\frac{181}{532}=–0.7$$

عالی! اگرچه، محاسبه این به صورت دستی زمان بر است، و بهترین استفاده از رایانه، محاسبه چیزها برای ما است. محاسبه همبستگی Spearman با توابع داخلی در پانداها واقعاً آسان و ساده است.

محاسبه ضریب همبستگی رتبه اسپیرمن با استفاده از پانداها

ضرایب همبستگی مختلف، از جمله اسپیرمن، را می توان از طریق محاسبه کرد corr() روش کتابخانه پاندا.

به عنوان یک آرگومان ورودی ، corr() تابع روش مورد استفاده برای محاسبه همبستگی را می پذیرد (spearman در مورد ما). روش نامیده می شود روی آ DataFrame، می گویند از اندازه mxn، که در آن هر ستون مقادیر یک متغیر تصادفی را نشان می دهد و m نمونه های کل هر متغیر را نشان می دهد.

برای n متغیرهای تصادفی ، آن را برمی گرداند nxn ماتریس مربع R. R(i,j) نشان دهنده ضریب همبستگی رتبه اسپیرمن بین متغیر تصادفی است i و j. از آنجایی که ضریب همبستگی بین یک متغیر و خودش 1 است، تمام ورودی های مورب (i,i) برابر با وحدت هستند. به اختصار:

$$\mathrm{آر}(\mathrm{من}،j)=\{\begin{array}{ll}{r}_{\mathrm{من}،j}& \text{اگر}\mathrm{من}\ne j\\ 1& \text{در غیر این صورت}\end{array}$$

توجه داشته باشید که ماتریس همبستگی متقارن است همانطور که همبستگی متقارن است، به عنوان مثال، M(i,j)=M(j,i). بیایید مثال ساده خود را از بخش قبل بگیریم و روش استفاده از پانداها را ببینیم. corr() تابع:

import numpy as np
import pandas as pd
import seaborn as sns 
import matplotlib.pyplot as plt

ما از Pandas برای خود محاسبات، Matplotlib با Seaborn برای تجسم و NumPy برای عملیات اضافی استفاده خواهیم کرد. روی داده.

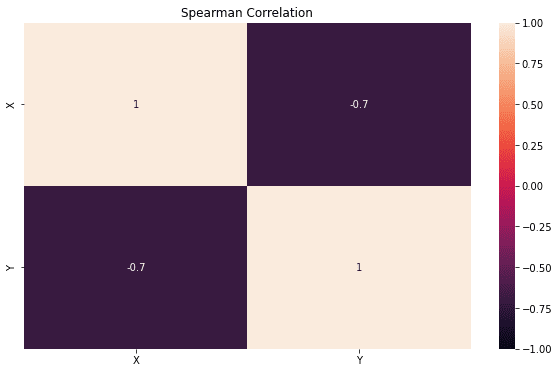
کد زیر ماتریس همبستگی اسپیرمن را محاسبه می کند روی چارچوب داده x_simple. توجه داشته باشید که آنهایی که روی قطرها، نشان می دهد که ضریب همبستگی یک متغیر با خودش به طور طبیعی است، یکی:

x_simple = pd.DataFrame(((-2,4),(-1,1),(0,3),(1,2),(2,0)),
                        columns=("X","Y"))
my_r = x_simple.corr(method="spearman")
print(my_r)

     X    Y
X  1.0 -0.7
Y -0.7  1.0

تجسم ضریب همبستگی

با توجه به ساختار جدول مانند شدت های محدود، (-1, 1) – یک روش طبیعی و راحت تجسم کردن ضریب همبستگی یک است نقشه حرارت.

اگر می‌خواهید درباره نقشه‌های حرارتی در Seaborn اطلاعات بیشتری کسب کنید، راهنمای نهایی ما برای نقشه‌های حرارتی در Seaborn با پایتون را بخوانید!

نقشه حرارتی شبکه‌ای از سلول‌ها است که در آن به هر سلول با توجه به مقدارش رنگی اختصاص داده می‌شود و این روش بصری تفسیر ماتریس‌های همبستگی برای ما بسیار آسان‌تر از تجزیه اعداد است. برای میزهای کوچکی مانند میزهای قبلی – کاملاً خوب است. اما با زیاد از بین متغیرها، تفسیر واقعی آنچه در حال انجام است بسیار دشوارتر است روی.

بیایید a را تعریف کنیم display_correlation() تابعی که ضریب همبستگی را محاسبه می کند و آن را به عنوان یک نقشه حرارتی نمایش می دهد:

def display_correlation(df):
    r = df.corr(method="spearman")
    plt.figure(figsize=(10,6))
    heatmap = sns.heatmap(df.corr(), vmin=-1, 
                      vmax=1, annot=True)
    plt.title("Spearman Correlation")
    return(r)

بیا تماس بگیریم display_correlation() روی ما r_simple DataFrame برای تجسم همبستگی Spearman:

r_simple=display_correlation(x_simple)

درک ضریب همبستگی اسپیرمن روی نمونه های مصنوعی

برای درک ضریب همبستگی اسپیرمن، اجازه دهید چند مثال مصنوعی ایجاد کنیم که روش عملکرد ضریب را برجسته می کند – قبل از اینکه به نمونه های طبیعی تر بپردازیم. این مثال‌ها به ما کمک می‌کنند بفهمیم این ضریب برای چه نوع روابطی +1، -1 یا نزدیک به صفر است.

قبل از تولید مثال‌ها، یک تابع کمکی جدید ایجاد می‌کنیم، plot_data_corr()، که تماس می گیرد display_correlation() و داده ها را در برابر X متغیر:

def plot_data_corr(df,title,color="green"):    
    r = display_correlation(df)
    fig, ax = plt.subplots(nrows=1, ncols=len(df.columns)-1,figsize=(14,3))
    for i in range(1,len(df.columns)):
        ax(i-1).scatter(df("X"),df.values(:,i),color=color)
        ax(i-1).title.set_text(title(i) +'\n r = ' + 
                             "{:.2f}".format(r.values(0,i)))
        ax(i-1).set(xlabel=df.columns(0),ylabel=df.columns(i))
    fig.subplots_adjust(wspace=.7)    
    plt.show()

توابع افزایش دهنده یکنواخت

بیایید با استفاده از NumPy چند توابع افزایش‌دهنده یکنواخت ایجاد کنیم و نگاهی به آن بیندازیم DataFrame پس از پر شدن با داده های مصنوعی:

seed = 11
rand = np.random.RandomState(seed)

x_incr = pd.DataFrame({"X":rand.uniform(0,10,100)})
x_incr("Line+") = x_incr.X*2+1
x_incr("Sq+") = x_incr.X**2
x_incr("Exp+") = np.exp(x_incr.X)
x_incr("Cube+") = (x_incr.X-5)**3

print(x_incr.head())

	ایکس	خط +	مربع +	Exp+	مکعب +
0	1.802697	4.605394	3.249716	6.065985	-32.685221
1	0.194752	1.389505	0.037929	1.215010	-110.955110
2	4.632185	10.264371	21.457140	102.738329	-0.049761
3	7.249339	15.498679	52.552920	1407.174809	11.380593
4	4.202036	9.404072	17.657107	66.822246	-0.508101

حالا بیایید به نقشه حرارتی همبستگی اسپیرمن و نمودار توابع مختلف در برابر آن نگاه کنیم X:

plot_data_corr(x_incr,("X","2X+1","$X^2$","$e^X$","$(X-5)^3$"))

ما می بینیم که برای همه این مثال ها، یک رابطه کاملاً یکنواخت بین متغیرها وجود دارد. همبستگی اسپیرمن یک +1 است، صرف نظر از اینکه متغیرها رابطه خطی یا غیرخطی دارند.

پیرسون از آنجایی که بر اساس محاسبه است، نتایج بسیار متفاوتی در اینجا ایجاد می شود روی را خطی رابطه بین متغیرها

تا زمانی که Y افزایش می یابد با افزایش X، بدون شکست، ضریب همبستگی رتبه اسپیرمن خواهد بود 1.

توابع کاهشی یکنواخت

بیایید همین مثال ها را تکرار کنیم روی توابع در حال کاهش یکنواخت ما دوباره داده های مصنوعی تولید می کنیم و همبستگی رتبه اسپیرمن را محاسبه می کنیم. ابتدا، اجازه دهید به 4 ردیف اول نگاه کنیم DataFrame:

x_decr = pd.DataFrame({"X":rand.uniform(0,10,100)})
x_decr("Line-") = -x_decr.X*2+1
x_decr("Sq-") = -x_decr.X**2
x_decr("Exp-") = np.exp(-x_decr.X)
x_decr("Cube-") = -(x_decr.X-5)**3
x_decr.head()

	ایکس	خط-	مربع	انقضا-	مکعب-
0	3.181872	-5.363744	-10.124309	0.041508	6.009985
1	2.180034	-3.360068	-4.752547	0.113038	22.424963
2	8.449385	-15.898771	-71.392112	0.000214	-41.041680
3	3.021647	-5.043294	-9.130350	0.048721	7.743039
4	4.382207	-7.764413	-19.203736	0.012498	0.235792

نقشه حرارتی ماتریس همبستگی و نمودار متغیرها در زیر آورده شده است:

plot_data_corr(x_decr,("X","-2X+1","$-X^2$","$-e^X$","$-(X-5)^3$"),"blue")

توابع غیر یکنواخت

مثال های زیر برای توابع مختلف غیر یکنواخت هستند. آخرین ستون به DataFrame متغیر مستقل است Rand، که هیچ ارتباطی با X.

این مثال ها همچنین باید روشن کنند که همبستگی اسپیرمن معیاری برای سنجش است یکنواختی رابطه بین دو متغیر ضریب صفر لزوماً نشان دهنده عدم وجود رابطه نیست، اما نشان دهنده عدم وجود رابطه است یکنواختی بین آنها.

قبل از تولید داده های مصنوعی، یک تابع کمکی دیگر را تعریف می کنیم، display_corr_pairs()، که تماس می گیرد display_correlation() برای نمایش نقشه حرارتی ماتریس همبستگی و سپس رسم تمام جفت متغیرها در DataFrame در مقابل یکدیگر با استفاده از کتابخانه Seaborn.

در مورب ها، هیستوگرام هر متغیر را با استفاده از رنگ زرد نشان خواهیم داد map_diag(). در زیر مورب ها، یک نمودار پراکندگی از همه جفت های متغیر می سازیم. از آنجایی که ماتریس همبستگی متقارن است، ما به نمودارهای بالای قطرها نیازی نداریم.

بیایید ضریب همبستگی پیرسون را نیز برای مقایسه نمایش دهیم:

def display_corr_pairs(df,color="cyan"):
    s = set_title = np.vectorize(lambda ax,r,rho: ax.title.set_text("r = " + 
                                        "{:.2f}".format(r) + 
                                        '\n $\\rho$ = ' + 
                                        "{:.2f}".format(rho)) if ax!=None else None
                            )      

    r = display_correlation(df)
    rho = df.corr(method="pearson")
    g = sns.PairGrid(df,corner=True)
    g.map_diag(plt.hist,color="yellow")
    g.map_lower(sns.scatterplot,color="magenta")
    set_title(g.axes,r,rho)
    plt.subplots_adjust(hspace = 0.6)
    plt.show()    

ما یک DataFrame غیر یکنواخت ایجاد خواهیم کرد، x_non، با این توابع از X:

• سهمی: \( (X-5)^2 \)

• Sin: \( \sin (\frac{X}{10}2\pi) \)

• Frac: \( \frac{X-5}{(X-5)^2+1} \)

• رند: اعداد تصادفی در محدوده (-1،1)

در زیر 4 خط اول از x_non:

x_non = pd.DataFrame({"X":rand.uniform(0,10,100)})
x_non("Parabola") = (x_non.X-5)**2
x_non("Sin") = np.sin(x_non.X/10*2*np.pi)
x_non("Frac") = (x_non.X-5)/((x_non.X-5)**2+1)
x_non("Rand") = rand.uniform(-1,1,100)

print(x_non.head())

	ایکس	سهمی	گناه	فراک	رند
0	0.654466	18.883667	0.399722	-0.218548	0.072827
1	5.746559	0.557351	-0.452063	0.479378	-0.818150
2	6.879362	3.532003	-0.924925	0.414687	-0.868501
3	5.683058	0.466569	-0.416124	0.465753	0.337066
4	6.037265	1.075920	-0.606565	0.499666	0.583229

ضریب همبستگی اسپیرمن بین جفت داده های مختلف در زیر نشان داده شده است:

display_corr_pairs(x_non)

این مثال‌ها نشان می‌دهند که همبستگی اسپیرمن برای چه نوع داده‌ای نزدیک به صفر است و در کجا مقادیر میانی دارد. نکته دیگری که باید به آن توجه داشت این است که همبستگی اسپیرمن و ضریب همبستگی پیرسون همیشه با یکدیگر همخوانی ندارند، بنابراین فقدان یکی به معنای فقدان دیگری نیست.

آنها برای آزمایش همبستگی برای جنبه های مختلف داده استفاده می شوند و نمی توانند به جای یکدیگر استفاده شوند. در حالی که آنها در برخی موارد موافق هستند، اما همیشه اینطور نیستند.

ضریب همبستگی اسپیرمن روی لینرود مجموعه داده

بیایید ضریب همبستگی اسپیرمن را اعمال کنیم روی یک مجموعه داده واقعی ما ساده را انتخاب کرده ایم مجموعه داده تمرینات بدنی تماس گرفت linnerud از sklearn.datasets بسته برای نمایش:

import sklearn.datasets.load_linnerud

کد زیر مجموعه داده را بارگیری می کند و متغیرها و ویژگی های هدف را در یک می پیوندد DataFrame. بیایید به 4 ردیف اول نگاه کنیم linnerud داده ها:

d=load_linnerud()

dat = pd.DataFrame(d.data,columns=d.feature_names)
alldat=dat.join(pd.DataFrame(d.target,columns=d.target_names) )
alldat.head()

	چانه	سیتوپ ها	می پرد	وزن	کمر	نبض
0	5.0	162.0	60.0	191.0	36.0	50.0
1	2.0	110.0	60.0	189.0	37.0	52.0
2	12.0	101.0	101.0	193.0	38.0	58.0
3	12.0	105.0	37.0	162.0	35.0	62.0
4	13.0	155.0	58.0	189.0	35.0	46.0

حالا بیایید جفت های همبستگی را با استفاده از ما نمایش دهیم display_corr_pairs() تابع:

display_corr_pairs(alldat)

با نگاهی به مقادیر همبستگی اسپیرمن، می‌توانیم نتایج جالبی از قبیل:

• مقادیر بالاتر دور کمر به معنی افزایش ارزش وزن (از r = 0.81)
• نشستن های بیشتر دارای مقادیر کمتری از کمر هستند (از r = -0.72)
• به نظر نمی رسد چانه ها، نشستن ها و پرش ها رابطه یکنواختی با نبض داشته باشند، زیرا مقادیر r مربوطه نزدیک به صفر هستند.

نتیجه گیری

در این راهنما، ضریب همبستگی رتبه اسپیرمن، بیان ریاضی آن، و محاسبه آن از طریق پایتون را مورد بحث قرار دادیم. pandas کتابخانه

ما این ضریب را نشان دادیم روی نمونه های مصنوعی مختلف و همچنین روی را Linnerrud مجموعه داده ضریب همبستگی Spearman یک اقدام ایده آل برای محاسبه یکنواختی رابطه بین دو متغیر است. با این حال ، یک مقدار نزدیک به صفر لزوماً نشان نمی دهد که متغیرها هیچ ارتباطی بین آنها ندارند.