از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
مرتب سازی شمارش در پایتون
سرفصلهای مطلب
معرفی
مرتبسازی شمارش یک الگوریتم مرتبسازی است که برای مرتبسازی عناصر یک آرایه استفاده میشود زمان خطی. ما معمولا از شمارش مرتب سازی برای مرتب سازی آرایه های عدد صحیح استفاده می کنیم.
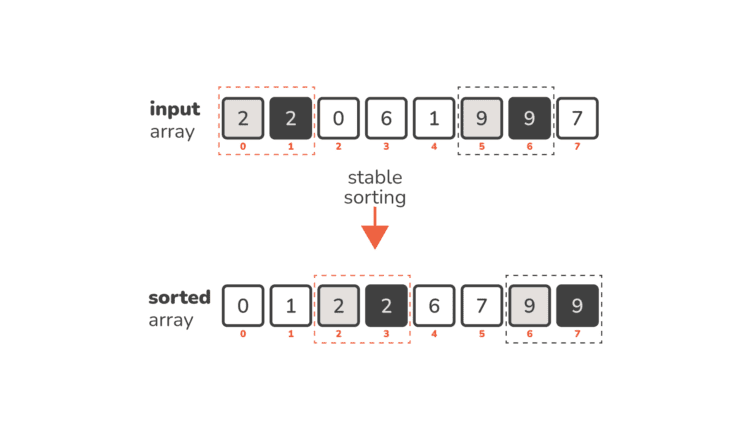
مرتب سازی شمارش یک است پایدار، الگوریتم غیر مقایسه ای.
غیر مقایسه ای الگوریتم های مرتب سازی مرتب سازی را بدون هیچ گونه مقایسه ای بین عناصری که باید مرتب شوند انجام می دهند.
پایدار الگوریتم های مرتب سازی ترتیب نسبی عناصر با مقدار یکسان را در آرایه مرتب شده حفظ می کنند. این بدان معناست که ترتیب نسبی دو عنصر هم ارزش در آرایه اصلی با ترتیب نسبی آنها در آرایه مرتب شده یکسان خواهد بود.

مرتب سازی شمارش است یک الگوریتم در محل نیست، از یک آرایه کمکی برای مرتب کردن عناصر یک آرایه ورودی استفاده می کند.
ایده پشت مرتب سازی شمارش
بیایید ابتدا نگاهی شهودی به روش عملکرد الگوریتم بیندازیم.
فرض کنید که آرایه را داریم I = (2, 2, 0, 6, 1, 9, 9, 7) و ما می خواهیم آن را مرتب کنیم. ما آرایه را فراخوانی می کنیم I را آرایه ورودی.
شمارش مرتب سازی با شمارش تعداد عناصری که با یک مقدار کلید مجزا مطابقت دارند کار می کند و سپس موقعیت های هر کلید را محاسبه می کند.
اول از همه، ما باید عنصری را با بالاترین مقدار پیدا کنیم، ما آن را حداکثر عنصر می نامیم – maxElement = 9.
سپس، یک آرایه کمکی با آن ایجاد می کنیم maxElement+1 عناصر، به نام آرایه شمارش (C). ما از آن برای ذخیره تعداد وقوع هر عنصر در آن استفاده خواهیم کرد آرایه ورودی I. بنابراین، همه شمارش ها باید به 0 مقداردهی شوند:
C = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
حال باید مراحل زیر را طی کنیم:
1. هر عنصر را مرور کنید آرایه ورودی و تعداد متناظر آن را افزایش دهید 1
به عنوان مثال، اگر به عنصری با مقدار آن برخورد کنیم 2 در آرایه ورودی (I، 1 را به عنصر با شاخص اضافه می کنیم 2 در آرایه شمارش:
I = (2, 2, 0, 6, 1, 9, 9, 7)
^
C = (0, 0, 1, 0, 0, 0, 0, 0, 0, 0)
پس از این مرحله، آرایه شمارش تعداد دفعات هر عنصر را در قسمت ذخیره می کند آرایه ورودی:
C = (1, 1, 2, 0, 0, 0, 1, 1, 0, 2)
2. برای هر عنصر در آرایه شمارش، مقدار آن را با مقدار تمام عناصر قبلی آن خلاصه کنید و آن مقدار را به عنوان مقدار عنصر فعلی ذخیره کنید:
C = (1, 2, 4, 4, 4, 4, 5, 6, 6, 8)
به این ترتیب، ما جمع تجمعی عناصر را ذخیره می کنیم آرایه شمارش، روی هر مرحله
3. محاسبه موقعیت عنصر بر اساس روی را آرایه شمارش ارزش های:
برای ذخیره این توالی مرتب شده، باید یک آرایه جدید ایجاد کنیم. بیایید اسمش را بگذاریم آرایه خروجی (O) و آن را با مقداردهی اولیه کنید k صفر، کجا k تعداد عناصر موجود در آرایه ورودی:
O = (0, 0, 0, 0, 0, 0, 0, 0) // Initialized output array
برای هر عنصر I(i) (شروع از انتها) در آرایه ورودی:
- شاخص را در آرایه شمارش که برابر با مقدار عنصر فعلی است
I(i)- این عنصر است
C(j)جایی کهj=I(i)
- این عنصر است
- تفریق کردن
1از ارزشC(i)- اکنون داریم
newValue = C(i)-1
- اکنون داریم
- ذخیره کنید
I(i)بهO(newValue) - را به روز کنید
C(i)باnewValue

در پایان، آرایه خروجی شامل عناصر مرتب شده آرایه ورودی است!
روش پیاده سازی مرتب سازی شمارش در پایتون
حالا، با وجود همه چیزهایی که در راه نیست – بیایید پیش برویم و مرتب سازی شمارش را در پایتون پیاده سازی کنیم:
def countingSort(inputArray):
maxElement= max(inputArray)
countArrayLength = maxElement+1
countArray = (0) * countArrayLength
for el in inputArray:
countArray(el) += 1
for i in range(1, countArrayLength):
countArray(i) += countArray(i-1)
outputArray = (0) * len(inputArray)
i = len(inputArray) - 1
while i >= 0:
currentEl = inputArray(i)
countArray(currentEl) -= 1
newPosition = countArray(currentEl)
outputArray(newPosition) = currentEl
i -= 1
return outputArray
inputArray = (2,2,0,6,1,9,9,7)
print("Input array = ", inputArray)
sortedArray = countingSort(inputArray)
print("Counting sort result = ", sortedArray)
با اجرای کد بالا خروجی زیر تولید می شود:
Input array = (2, 2, 0, 6, 1, 9, 9, 7)
Counting sort result = (0, 1, 2, 2, 6, 7, 9, 9)
پیچیدگی الگوریتم مرتب سازی شمارش
الگوریتم مرتب سازی شمارش فقط از ساده استفاده می کند برای و در حالی که حلقهها بدون بازگشتهای پیچیده و فراخوانیهای زیرمجموعه، بنابراین، تحلیل پیچیدگی آن بسیار ساده است. process.
قبل از اینکه به تحلیل پیچیدگی بپردازیم، اجازه دهید طول آرایه ورودی را به صورت برچسب گذاری کنیم n و مقدار حداکثر عنصر در آرایه ورودی به عنوان k.
پیچیدگی زمانی
مرحله اول الگوریتم روی آرایه ورودی n بار تکرار می شود تا آرایه شمارش را مقداردهی اولیه کند، بنابراین دارای پیچیدگی بر).
مرحله دوم با تعداد k بار تکرار می شود تا مجموع تجمعی هر عنصر را محاسبه کند، بنابراین پیچیدگی آن خوب).
مرحله سوم مرتب سازی را بر اساس انجام می دهد روی آرایه شمارش، بنابراین باید در یک حلقه while تکرار شود n بارها، بنابراین دارای پیچیدگی است بر).
به طور جمعی، پیچیدگی زمانی الگوریتم مرتب سازی شمارش O(n+k) است.
پیچیدگی فضا
استفاده از مرتب سازی شمارش ورودی و آرایه خروجی، هر دو از طول n و یکی آرایه شمارش از طول (k+1).
از این رو، کل فضایی که این الگوریتم استفاده می کند O(n+k) است.
نتیجه
در مجموع، شمارش مرتب سازی یک الگوریتم مرتب سازی عالی و کارآمد و در عین حال ساده است. در شرایط ایده آل، درک و یادگیری آن واقعا آسان است، اما همچنان می تواند پیچیدگی خطی را حفظ کند.
مشکل واقعی زمانی رخ می دهد که مقدار بزرگترین عنصر باشد k از تعداد عناصر موجود در آرایه ورودی بیشتر است n. به عنوان k نزدیک می شود n²، پیچیدگی زمانی مرتبسازی شمارش نزدیکتر میشود O (n²)، که پیچیدگی زمانی وحشتناکی برای الگوریتم مرتب سازی است. بنابراین، اگر آرایه ورودی دارای طیف وسیعی از مقادیر است، استفاده از مرتب سازی شمارش توصیه نمی شود.
در حالت ایدهآل، از مرتبسازی شمارش برای مرتبسازی برخی از آرایههای عدد صحیح با محدودهای از مقادیر کوچک یا بهعنوان زیربرنامه برای برخی دیگر از الگوریتمهای مرتبسازی، مانند مرتبسازی رادیکس، استفاده میکنیم. به این ترتیب، ما از حداکثر کردن پتانسیل کامل مرتب سازی شمارش اطمینان حاصل خواهیم کرد، در حالی که هنوز از همه موارد استفاده غیربهینه اجتناب می کنیم.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-10 06:15:05



