سرور مجازی NVMe

Gradient Descent در پایتون: پیاده سازی و نظریه

Pythonبرنامه نویسی

توسط مهران در دی ۲۵, ۱۴۰۲

سرفصلهای مطلب

زمان لازم برای مطالعه: 9 دقیقه

معرفی

این آموزش مقدمه ای است بر یک تکنیک بهینه سازی ساده به نام شیب نزول، که در پیشرفته ترین مدل های یادگیری ماشین کاربرد عمده ای داشته است.

ما یک روال هدف کلی برای پیاده سازی گرادیان نزول و اعمال آن برای حل مسائل مختلف، از جمله طبقه بندی از طریق یادگیری نظارت شده، ایجاد خواهیم کرد.

در این process، ما بینشی در مورد عملکرد این الگوریتم به دست خواهیم آورد و تأثیر پارامترهای مختلف فراپارامتر را مطالعه خواهیم کرد. روی عملکرد آن ما هم میریم نزول شیب دسته ای و تصادفی انواع به عنوان نمونه

Gradient Descent چیست؟

گرادیان نزول یک تکنیک بهینه سازی است که می تواند آن را پیدا کند کمترین از یک تابع هدف. این یک تکنیک حریصانه است که با گام برداشتن در جهت حداکثر نرخ کاهش تابع، راه حل بهینه را پیدا می کند.

در مقابل، شیب صعود یک همتای نزدیک است که می یابد بیشترین یک تابع با پیروی از جهت حداکثر نرخ افزایش تابع.

برای درک روش عملکرد نزول گرادیان، یک تابع چند متغیره $f(\textbf{w})$ را در نظر بگیرید، جایی که $\textbf w = (w_1, w_2, \ldots, w_n)^T $. برای یافتن $ \textbf{w} $ که در آن این تابع به حداقل می رسد، گرادیان نزول از مراحل زیر استفاده می کند:

مقدار تصادفی اولیه $ \textbf{w} $ را انتخاب کنید
تعداد حداکثر تکرار را انتخاب کنید T
یک مقدار برای میزان یادگیری $ \eta \in (a,b) $
دو مرحله را تا زمانی که $f$ تغییر نکند یا تکرارها از T بیشتر شود تکرار کنید

a. محاسبه: $ \Delta \textbf{w} = – \eta \nabla_\textbf{w} f(\textbf{w}) $

ب به روز رسانی $\textbf{w} $ به صورت: $\textbf{w} \lefttarrow \textbf{w} + \Delta \textbf{w} $

نماد فلش سمت چپ از نظر ریاضی روشی صحیح برای نوشتن بیانیه انتساب است.

در اینجا $ \nabla_\textbf{w} f $ نشان دهنده گرادیان $f$ است که توسط:
$$
\nabla_\textbf{w} f(\textbf{w}) =
\begin{bmatrix}
\frac{\partial f(\textbf{w})}{\partial w_1} \
\frac{\partial f(\textbf{w})}{\partial w_2} \
\vdots\
\frac{\partial f(\textbf{w})}{\partial w_n}
\end{bmatrix}
$$

یک تابع مثال از دو متغیر $f(w_1,w_2) = w_1^2+w_2^2 $ را در نظر بگیرید، سپس در هر تکرار $ ((w_1,w_2) $ به‌صورت به‌روزرسانی می‌شود:

$$
\شروع {bmatrix}
w_1 \ w_2
\end {bmatrix} \lefttarrow
\شروع {bmatrix}
w_1 \ w_2
\end {bmatrix} – \eta
\شروع {bmatrix}
2w_1 \ 2w_2
\پایان {bmatrix}
$$

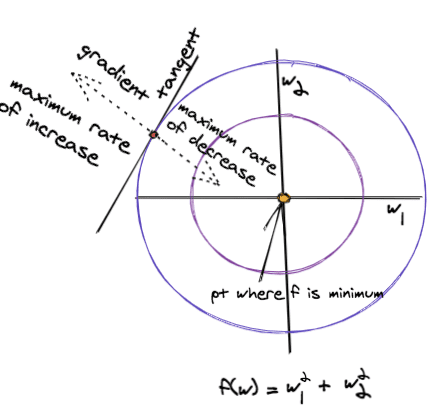
شکل زیر روش عملکرد شیب نزول را نشان می دهد روی این تابع

دایره ها خطوط این تابع هستند. اگر در امتداد یک کانتور حرکت کنیم، مقدار تابع تغییر نمی کند و باقی می ماند a ثابت.

این با جهت گرادیان مخالف است، جایی که تابع با حداکثر نرخ تغییر می کند. بنابراین جهت گرادیان تابع در هر نقطه نسبت به مماس کانتور در آن نقطه نرمال است.

به عبارت ساده، گرادیان را می توان به عنوان یک فلش در نظر گرفت که در جهتی است که تابع بیشترین تغییر را دارد.

پیروی از جهت گرادیان منفی منجر به نقاطی می شود که مقدار تابع با حداکثر نرخ کاهش می یابد. این میزان یادگیری، همچنین به نام اندازه گام، تعیین می کند که چقدر سریع یا آهسته در جهت گرادیان حرکت کنیم.

اضافه کردن مومنتوم

هنگام استفاده از نزول گرادیان، با مشکلات زیر مواجه می شویم:

گرفتار شدن در حداقل محلی، که نتیجه مستقیم حریص بودن این الگوریتم است
بیش از حد و از دست دادن بهینه جهانی، این نتیجه مستقیم حرکت بیش از حد سریع در جهت گرادیان است
نوسان، این پدیده‌ای است که زمانی رخ می‌دهد که مقدار تابع بدون توجه به جهتی که پیشروی می‌کند، به‌طور قابل توجهی تغییر نمی‌کند. شما می توانید آن را به عنوان حرکت در یک فلات در نظر بگیرید، مهم نیست که کجا بروید در همان ارتفاع هستید

برای مبارزه با این مشکلات، یک اصطلاح حرکتی $ \alpha $ به عبارت $\Delta \textbf{w}$ اضافه می‌شود تا نرخ یادگیری را هنگام حرکت به سمت مقدار بهینه جهانی تثبیت کند.

در زیر، ما از بالانویس $i$ برای نشان دادن شماره تکرار استفاده می کنیم:
$$
\Delta \textbf{w}^i = – \eta \nabla_\textbf{w} f(\textbf{w}^i) + \alpha \textbf{w}^{i-1}
$$

پیاده سازی Gradient Descent در پایتون

قبل از شروع نوشتن کد واقعی برای نزول گرادیان، اجازه دهید import چند کتابخانه که برای کمک به ما از آنها استفاده خواهیم کرد:

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import sklearn.datasets as dt
from sklearn.model_selection import train_test_split

حالا، با این که از راه نیست، بیایید جلو برویم و a را تعریف کنیم gradient_descent() تابع. در این تابع، حلقه زمانی به پایان می رسد که:

تعداد تکرارها از حداکثر مقدار بیشتر است
تفاوت در مقادیر تابع بین دو تکرار متوالی کمتر از یک آستانه مشخص است

پارامترها در هر تکرار با توجه به گرادیان تابع هدف به روز می شوند.

تابع پارامترهای زیر را می پذیرد:

max_iterations: حداکثر تعداد تکرار برای اجرا
threshold: اگر تفاوت در مقادیر تابع بین دو تکرار متوالی کمتر از این آستانه باشد، متوقف شود
w_init: نقطه اولیه از جایی که نزول گرادیان را شروع کنیم
obj_func: اشاره به تابعی که تابع هدف را محاسبه می کند
grad_func: اشاره به تابعی که گرادیان تابع را محاسبه می کند
extra_param: پارامترهای اضافی (در صورت نیاز) برای obj_func و grad_func
learning_rate: اندازه پله برای نزول گرادیان. باید در (0،1) باشد
momentum: حرکت برای استفاده. باید در (0،1) باشد

همچنین، تابع باز خواهد گشت:

w_history: تمام نقاط در فضا، بازدید شده توسط نزول گرادیان که در آن تابع هدف ارزیابی شد
f_history: مقدار متناظر تابع هدف محاسبه شده در هر نقطه



def gradient_descent(max_iterations,threshold,w_init,
                     obj_func,grad_func,extra_param = (),
                     learning_rate=0.05,momentum=0.8):
    
    w = w_init
    w_history = w
    f_history = obj_func(w,extra_param)
    delta_w = np.zeros(w.shape)
    i = 0
    diff = 1.0e10
    
    while  i<max_iterations and diff>threshold:
        delta_w = -learning_rate*grad_func(w,extra_param) + momentum*delta_w
        w = w+delta_w
        
        
        w_history = np.vstack((w_history,w))
        f_history = np.vstack((f_history,obj_func(w,extra_param)))
        
        
        
        i+=1
        diff = np.absolute(f_history(-1)-f_history(-2))
    
    return w_history,f_history

بهینه سازی توابع با Gradient Descent

اکنون که یک پیاده‌سازی با هدف کلی از گرادیان نزول داریم، اجازه دهید آن را اجرا کنیم روی تابع دو بعدی مثال ما $f(w_1,w_2) = w_1^2+w_2^2 $ با خطوط دایره ای.

تابع دارای حداقل مقدار صفر در مبدا است. بیایید ابتدا تابع را تجسم کنیم و سپس حداقل مقدار آن را پیدا کنیم.

تجسم تابع هدف f(x)

این visualize_fw() تابع زیر، 2500 نقطه با فاصله مساوی ایجاد می کند روی یک شبکه و مقدار تابع را در هر نقطه محاسبه می کند.

این function_plot() تابع بسته به مقدار $f(\textbf w)$ در آن نقطه، تمام نقاط را با رنگ های مختلف نمایش می دهد. همه نقاطی که مقدار تابع در آنها یکسان است، رنگ یکسانی دارند:

def visualize_fw():
    xcoord = np.linspace(-10.0,10.0,50)
    ycoord = np.linspace(-10.0,10.0,50)
    w1,w2 = np.meshgrid(xcoord,ycoord)
    pts = np.vstack((w1.flatten(),w2.flatten()))
    
    
    pts = pts.transpose()
    
    
    f_vals = np.sum(pts*pts,axis=1)
    function_plot(pts,f_vals)
    plt.title('Objective Function Shown in Color')
    plt.show()
    return pts,f_vals


def annotate_pt(text,xy,xytext,color):
    plt.plot(xy(0),xy(1),marker='P',markersize=10,c=color)
    plt.annotate(text,xy=xy,xytext=xytext,
                 
                 arrowprops=dict(arrowstyle="->",
                 color = color,
                 connectionstyle='arc3'))



def function_plot(pts,f_val):
    f_plot = plt.scatter(pts(:,0),pts(:,1),
                         c=f_val,vmin=min(f_val),vmax=max(f_val),
                         cmap='RdBu_r')
    plt.colorbar(f_plot)
    
    annotate_pt('global minimum',(0,0),(-5,-7),'yellow')    

pts,f_vals = visualize_fw()

در حال اجرا Gradient Descent با هایپرپارامترهای مختلف

اکنون زمان اجرای گرادیان نزول است تا تابع هدف خود را به حداقل برسانیم. تماس گرفتن gradient_descent()، دو تابع تعریف می کنیم:

f(): تابع هدف را در هر نقطه محاسبه می کند w
grad(): گرادیان را در هر نقطه محاسبه می کند w

برای درک تأثیر پارامترهای مختلف روی شیب نزول، تابع solve_fw() تماس می گیرد gradient_descent() با 5 تکرار برای مقادیر مختلف نرخ یادگیری و حرکت.

کارکرد visualize_learning()، مقادیر $(w_1,w_2) $ را رسم می کند و مقادیر تابع را با رنگ های مختلف نشان می دهد. فلش های موجود در طرح ردیابی اینکه کدام نقطه از آخرین نقطه به روز شده است را آسان تر می کند:


def f(w,extra=()):
    return np.sum(w*w)


def grad(w,extra=()):
    return 2*w




def visualize_learning(w_history):  
    
    
    function_plot(pts,f_vals)
    
    
    plt.plot(w_history(:,0),w_history(:,1),marker='o',c='magenta') 
    
    
    annotate_pt('minimum found',
                (w_history(-1,0),w_history(-1,1)),
                (-1,7),'green')
    iter = w_history.shape(0)
    for w,i in zip(w_history,range(iter-1)):
        
        plt.annotate("",
                    xy=w, xycoords='data',
                    xytext=w_history(i+1,:), textcoords='data',
                    arrowprops=dict(arrowstyle='<-',
                            connectionstyle='angle3'))     
    
def solve_fw():
    
    rand = np.random.RandomState(19)
    w_init = rand.uniform(-10,10,2)
    fig, ax = plt.subplots(nrows=4, ncols=4, figsize=(18, 12))
    learning_rates = (0.05,0.2,0.5,0.8)
    momentum = (0,0.5,0.9)
    ind = 1
    
    
    for alpha in momentum:
        for eta,col in zip(learning_rates,(0,1,2,3)):
            plt.subplot(3,4,ind)        
            w_history,f_history = gradient_descent(5,-1,w_init, f,grad,(),eta,alpha)
            
            visualize_learning(w_history)
            ind = ind+1
            plt.text(-9, 12,'Learning Rate = '+str(eta),fontsize=13)
            if col==1:
                plt.text(10,15,'momentum = ' + str(alpha),fontsize=20)

    fig.subplots_adjust(hspace=0.5, wspace=.3)
    plt.show()

بریم بدویم solve_fw() و ببینید نرخ یادگیری و تکانه چگونه بر نزول گرادیان تأثیر می گذارد:

solve_fw()

این مثال نقش حرکت و سرعت یادگیری را روشن می کند.

در نمودار اول، با اندازه حرکت صفر و نرخ یادگیری 0.05، یادگیری کند است و الگوریتم به حداقل جهانی نمی رسد. همانطور که از نمودارهای ستون اول می بینیم، افزایش تکانه سرعت یادگیری را افزایش می دهد. افراطی دیگر آخرین ستون است که در آن نرخ یادگیری بالا نگه داشته می شود. این باعث ایجاد نوساناتی می شود که با افزودن تکانه تا حدی می توان آنها را کنترل کرد.

دستورالعمل کلی برای نزول گرادیان استفاده از مقادیر کوچک نرخ یادگیری و مقادیر بالاتر تکانه است.

Gradient Descent برای به حداقل رساندن خطای میانگین مربع

گرادیان نزول یک تکنیک خوب و ساده برای به حداقل رساندن میانگین مربعات خطا در طبقه بندی نظارت شده یا مسئله رگرسیون است.

فرض کنید به ما مثال های آموزشی $m$ $(x_{ij})$ با $i=1\ldots m$ داده شده است، که در آن هر مثال دارای $n$ ویژگی است، به عنوان مثال، $j= 1\ldots n $. اگر مقادیر هدف و خروجی مربوطه برای هر مثال به ترتیب $t_i$ و $o_i$ باشد، آنگاه تابع مربع خطای میانگین $E$ (در این مورد تابع شی ما) به صورت زیر تعریف می شود:

$$
E = \frac{1}{m} \Sigma_{i=1}^m (t_i – o_i)^2
$$

جایی که خروجی $o_i$ توسط یک ترکیب خطی وزنی از ورودی ها تعیین می شود که توسط:

$$
o_i = w_0 + w_1 x_{i1} + w_2 x_{i2} + \ldots + w_n x_{in}
$$

پارامتر مجهول در معادله بالا بردار وزن $\textbf w = (w_0,w_1,\ldots,w_n)^T$ است.

تابع هدف در این حالت میانگین مربعات خطا با گرادیان است که توسط:

$$
\nabla_{\textbf w}E(\textbf w) = -\Sigma_{i=1}^{m} (t_i – o_i) \textbf{x}_i
$$

جایی که $x_{i}$ i-امین مثال است. یا مجموعه ای از ویژگی های اندازه n.

تنها چیزی که اکنون نیاز داریم یک تابع برای محاسبه گرادیان و یک تابع برای محاسبه میانگین مربعات خطا است.

این gradient_descent() سپس می توان از تابع همانطور که هست استفاده کرد. توجه داشته باشید که هنگام محاسبه گرادیان، تمام مثال های آموزشی با هم پردازش می شوند. از این رو، این نسخه از شیب نزول برای به روز رسانی وزن ها به عنوان نامیده می شود به روز رسانی دسته ای یا یادگیری دسته ای:


def grad_mse(w,xy):
    (x,y) = xy
    (rows,cols) = x.shape
    
    
    o = np.sum(x*w,axis=1)
    diff = y-o
    diff = diff.reshape((rows,1))    
    diff = np.tile(diff, (1, cols))
    grad = diff*x
    grad = -np.sum(grad,axis=0)
    return grad


def mse(w,xy):
    (x,y) = xy
    
    
    
    
    o = np.sum(x*w,axis=1)
    mse = np.sum((y-o)*(y-o))
    mse = mse/2
    return mse

در حال اجرا Gradient Descent روی OCR

برای نشان دادن نزول گرادیان روی یک مشکل طبقه‌بندی، ما مجموعه داده‌های رقمی را انتخاب کرده‌ایم sklearn.datasets.

برای ساده نگه داشتن همه چیز، بیایید یک اجرای آزمایشی نزول گرادیان را انجام دهیم روی یک مسئله دو کلاسه (رقم 0 در مقابل رقم 1). کد زیر ارقام را بارگیری می کند و 10 رقم اول را نمایش می دهد. این به ما ایده ای از ماهیت نکات آموزشی می دهد:


digits,target = dt.load_digits(n_class=2,return_X_y=True)
fig,ax = plt.subplots(nrows=1, ncols=10,figsize=(12,4),subplot_kw=dict(xticks=(), yticks=()))


for i in np.arange(10):
    ax(i).imshow(digits(i,:).reshape(8,8),cmap=plt.cm.gray)   
plt.show()

ما هم به روش نیاز داریم train_test_split از جانب sklearn.model_selection برای تقسیم داده های آموزشی به یک قطار و یک مجموعه آزمایشی. کد زیر gradient descent را اجرا می کند روی مجموعه آموزشی، وزن ها را یاد می گیرد و میانگین مربعات خطا را در تکرارهای مختلف رسم می کند.

هنگام اجرای شیب نزول، سرعت و تکانه یادگیری را بسیار کوچک نگه می‌داریم زیرا ورودی‌ها عادی یا استاندارد نشده‌اند. همچنین، نسخه دسته ای نزول گرادیان به نرخ یادگیری کمتری نیاز دارد:


x_train, x_test, y_train, y_test = train_test_split(
                        digits, target, test_size=0.2, random_state=10)


x_train = np.hstack((np.ones((y_train.size,1)),x_train))
x_test  = np.hstack((np.ones((y_test.size,1)),x_test))


rand = np.random.RandomState(19)
w_init = rand.uniform(-1,1,x_train.shape(1))*.000001
w_history,mse_history = gradient_descent(100,0.1,w_init,
                              mse,grad_mse,(x_train,y_train),
                             learning_rate=1e-6,momentum=0.7)


plt.plot(np.arange(mse_history.size),mse_history)
plt.xlabel('Iteration No.')
plt.ylabel('Mean Square Error')
plt.title('Gradient Descent روی Digits Data (Batch Version)')
plt.show()

این عالی به نظر می رسد! بیایید میزان خطای OCR خود را بررسی کنیم روی داده های آموزش و آزمون در زیر تابع کوچکی برای محاسبه میزان خطای طبقه بندی وجود دارد که به آن گفته می شود روی مجموعه آموزش و آزمون:



def error(w,xy):
    (x,y) = xy
    o = np.sum(x*w,axis=1)
    
    
    ind_1 = np.where(o>0.5)
    ind_0 = np.where(o<=0.5)
    o(ind_1) = 1
    o(ind_0) = 0
    return np.sum((o-y)*(o-y))/y.size*100
    
train_error = error(w_history(-1),(x_train,y_train))
test_error = error(w_history(-1),(x_test,y_test))

print("Train Error Rate: " + "{:.2f}".format(train_error))
print("Test Error Rate: " + "{:.2f}".format(test_error))

Train Error Rate: 0.69
Test Error Rate: 1.39

نزول گرادیان تصادفی در پایتون

در بخش قبل، از طرح به‌روزرسانی دسته‌ای برای نزول گرادیان استفاده کردیم.

نسخه دیگری از نزول گرادیان است برخط یا تصادفی طرح به روز رسانی، که در آن هر نمونه تمرینی یک به یک برای به روز رسانی وزنه ها گرفته می شود.

هنگامی که تمام نمونه های آموزشی چرخه ای می شوند، می گوییم که یک دوره کامل شده است. برای نتایج بهتر، نمونه‌های آموزشی قبل از هر دوره با هم مخلوط می‌شوند.

قطعه کد زیر یک تغییر جزئی در آن است gradient_descent() تابع برای ترکیب همتای تصادفی خود. این تابع به جای پارامتر اضافی، (مجموعه آموزشی، هدف) را به عنوان پارامتر می گیرد. اصطلاح “تکرار” به “دوران” تغییر نام داده است:


def stochastic_gradient_descent(max_epochs,threshold,w_init,
                                obj_func,grad_func,xy,
                                learning_rate=0.05,momentum=0.8):
    (x_train,y_train) = xy
    w = w_init
    w_history = w
    f_history = obj_func(w,xy)
    delta_w = np.zeros(w.shape)
    i = 0
    diff = 1.0e10
    rows = x_train.shape(0)
    
    
    while  i<max_epochs and diff>threshold:
        
        np.random.seed(i)
        p = np.random.permutation(rows)
        
        
        for x,y in zip(x_train(p,:),y_train(p)):
            delta_w = -learning_rate*grad_func(w,(np.array((x)),y)) + momentum*delta_w
            w = w+delta_w
            
        i+=1
        w_history = np.vstack((w_history,w))
        f_history = np.vstack((f_history,obj_func(w,xy)))
        diff = np.absolute(f_history(-1)-f_history(-2))
        
    return w_history,f_history

بیایید کد را اجرا کنیم تا ببینیم نتایج برای نسخه تصادفی گرادیان نزول چگونه است:

rand = np.random.RandomState(19)
w_init = rand.uniform(-1,1,x_train.shape(1))*.000001
w_history_stoch,mse_history_stoch = stochastic_gradient_descent(
                                100,0.1,w_init,
                              mse,grad_mse,(x_train,y_train),
                             learning_rate=1e-6,momentum=0.7)


plt.plot(np.arange(mse_history_stoch.size),mse_history_stoch)
plt.xlabel('Iteration No.')
plt.ylabel('Mean Square Error')
plt.title('Gradient Descent روی Digits Data (Stochastic Version)')

plt.show()

بیایید میزان خطا را نیز بررسی کنیم:

train_error_stochastic = error(w_history_stoch(-1),(x_train,y_train))
test_error_stochastic = error(w_history_stoch(-1),(x_test,y_test))

print("Train Error rate with Stochastic Gradient Descent: " + 
      "{:.2f}".format(train_error_stochastic))
print("Test Error rate with Stochastic Gradient Descent: "  
      + "{:.2f}".format(test_error_stochastic))

Train Error rate with Stochastic Gradient Descent: 0.35
Test Error rate with Stochastic Gradient Descent: 1.39

مقایسه نسخه های دسته ای و تصادفی

اکنون بیایید هر دو نسخه دسته ای و تصادفی نزول گرادیان را با هم مقایسه کنیم.

ما نرخ یادگیری را برای هر دو نسخه به یک مقدار ثابت می کنیم و تکانه را تغییر می دهیم تا ببینیم هر دو با چه سرعتی همگرا می شوند. وزن های اولیه و معیارهای توقف برای هر دو الگوریتم یکسان باقی می مانند:

fig, ax = plt.subplots(nrows=3, ncols=1, figsize=(10,3))

rand = np.random.RandomState(11)
w_init = rand.uniform(-1,1,x_train.shape(1))*.000001
eta = 1e-6
for alpha,ind in zip((0,0.5,0.9),(1,2,3)):
    w_history,mse_history = gradient_descent(
                                100,0.01,w_init,
                              mse,grad_mse,(x_train,y_train),
                             learning_rate=eta,momentum=alpha)

    w_history_stoch,mse_history_stoch = stochastic_gradient_descent(
                                100,0.01,w_init,
                              mse,grad_mse,(x_train,y_train),
                             learning_rate=eta,momentum=alpha)
    
    
    plt.subplot(130+ind)
    plt.plot(np.arange(mse_history.size),mse_history,color='green')
    plt.plot(np.arange(mse_history_stoch.size),mse_history_stoch,color='blue')
    plt.legend(('batch','stochastic'))
    
    
    plt.text(3,-30,'Batch: Iterations='+
             str(mse_history.size) )
    plt.text(3,-45,'Stochastic: Iterations='+
             str(mse_history_stoch.size))
    plt.title('Momentum = ' + str(alpha))   
    
    
    train_error = error(w_history(-1),(x_train,y_train))
    test_error = error(w_history(-1),(x_test,y_test))
    
    train_error_stochastic = error(w_history_stoch(-1),(x_train,y_train))
    test_error_stochastic = error(w_history_stoch(-1),(x_test,y_test))
    
    print ('Momentum = '+str(alpha))
    
    print ('\tBatch:')
    print ('\t\tTrain error: ' + "{:.2f}".format(train_error) )
    print ('\t\tTest error: ' + "{:.2f}".format(test_error) )
    
    print ('\tStochastic:')
    print ('\t\tTrain error: ' + "{:.2f}".format(train_error_stochastic) )
    print ('\t\tTest error: ' + "{:.2f}".format(test_error_stochastic) )
    
        
plt.show()

Momentum = 0
    Batch:
        Train error: 0.35
        Test error: 1.39
    Stochastic:
        Train error: 0.35
        Test error: 1.39
Momentum = 0.5
    Batch:
        Train error: 0.00
        Test error: 1.39
    Stochastic:
        Train error: 0.35
        Test error: 1.39
Momentum = 0.9
    Batch:
        Train error: 0.00
        Test error: 1.39
    Stochastic:
        Train error: 0.00
        Test error: 1.39

در حالی که تفاوت قابل‌توجهی در دقت بین دو نسخه طبقه‌بندی‌کننده وجود ندارد، نسخه تصادفی برنده آشکاری در مورد سرعت هم‌گرایی است. تکرارهای کمتری طول می‌کشد تا به نتیجه‌ای مشابه با همتای دسته‌ای خود برسید.

نتیجه گیری

شیب نزول یک تکنیک ساده و آسان برای پیاده سازی است.

در این آموزش، نزول گرادیان را نشان دادیم روی تابعی از دو متغیر با خطوط دایره ای. سپس مثال خود را برای به حداقل رساندن میانگین مربعات خطا در یک مسئله طبقه بندی گسترش دادیم و یک سیستم OCR ساده ساختیم. ما همچنین در مورد نسخه تصادفی نزول گرادیان بحث کردیم.

یک تابع هدف کلی برای اجرای گرادیان نزول در این آموزش توسعه داده شد. ما خوانندگان را تشویق می کنیم که از این تابع استفاده کنند روی مشکلات رگرسیون و طبقه بندی مختلف، با پارامترهای مختلف، برای درک بهتر عملکرد آن.

(برچسب‌ها به ترجمه)# python

منتشر شده در 1403-01-15 03:09:04

امتیاز شما به این مطلب