از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
تولید داده های مصنوعی با Numpy و Scikit-Learn
سرفصلهای مطلب
معرفی
در این آموزش، جزئیات تولید مجموعه داده های مصنوعی مختلف با استفاده از ناامپی و Scikit- Learn کتابخانه ها خواهیم دید که چگونه می توان نمونه های مختلف را از توزیع های مختلف با پارامترهای شناخته شده تولید کرد.
همچنین در مورد تولید مجموعه داده ها برای اهداف مختلف، مانند رگرسیون، طبقه بندی و خوشه بندی بحث خواهیم کرد. در پایان خواهیم دید که چگونه می توانیم مجموعه داده ای تولید کنیم که توزیع یک مجموعه داده موجود را تقلید کند.
نیاز به داده های مصنوعی
در علم داده، داده های مصنوعی نقش بسیار مهمی دارند. این به ما امکان می دهد الگوریتم جدیدی را تحت شرایط کنترل شده آزمایش کنیم. به عبارت دیگر، میتوانیم دادههایی تولید کنیم که ویژگی یا رفتار بسیار خاصی از الگوریتم ما را آزمایش کند.
به عنوان مثال می توانیم عملکرد آن را آزمایش کنیم روی مجموعه داده های متعادل در مقابل نامتعادل، یا می توانیم عملکرد آن را در سطوح مختلف نویز ارزیابی کنیم. با انجام این کار، میتوانیم یک خط پایه از عملکرد الگوریتم خود تحت سناریوهای مختلف ایجاد کنیم.
موارد بسیار دیگری وجود دارد که ممکن است به داده های مصنوعی نیاز باشد. به عنوان مثال، به دست آوردن داده های واقعی ممکن است سخت یا پرهزینه باشد، یا ممکن است نقاط داده بسیار کمی داشته باشند. دلیل دیگر حریم خصوصی است، جایی که داده های واقعی را نمی توان برای دیگران فاش کرد.
راه اندازی
قبل از نوشتن کد برای تولید داده های مصنوعی، اجازه دهید import کتابخانه های مورد نیاز:
import numpy as np
import matplotlib.colors
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sklearn.datasets as dt
from sklearn.neighbors import KernelDensity
from sklearn.model_selection import GridSearchCV
سپس، در ابتدا چند متغیر مفید خواهیم داشت:
seed = 11
rand_state = 11
color_map = plt.cm.get_cmap('RdYlBu')
color_map_discrete = matplotlib.colors.LinearSegmentedColormap.from_list("", ("red","cyan","magenta","blue"))
تولید نمونه های 1 بعدی از توزیع های شناخته شده
اکنون، ما در مورد تولید نقاط نمونه از توزیع های شناخته شده در یک بعدی صحبت خواهیم کرد.
را random ماژول از numpy طیف گسترده ای از راه ها را برای تولید اعداد تصادفی نمونه برداری شده از یک توزیع شناخته شده با مجموعه ای ثابت از پارامترها ارائه می دهد. برای اهداف بازتولید، ما را تصویب خواهیم کرد seed به RandomState تماس بگیرید و تا زمانی که از همان seed استفاده می کنیم، همان شماره ها را دریافت می کنیم.
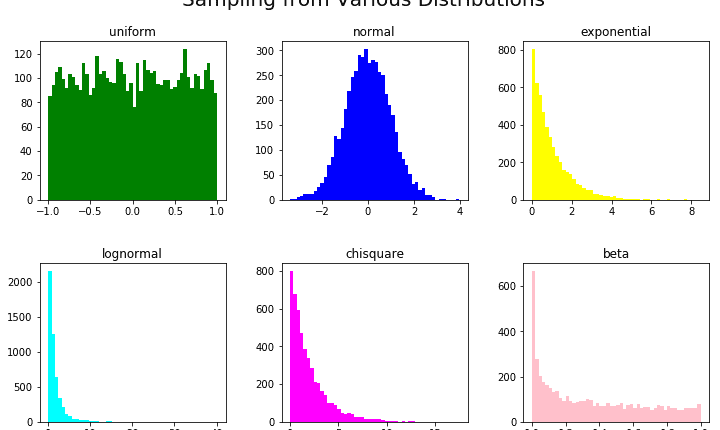
بیایید یک لیست توزیع تعریف کنیم، مانند uniform، normal، exponentialو غیره، یک لیست پارامتر، و یک لیست رنگی به طوری که ما بتوانیم بین این موارد به صورت بصری تشخیص دهیم:
rand = np.random.RandomState(seed)
dist_list = ('uniform','normal','exponential','lognormal','chisquare','beta')
param_list = ('-1,1','0,1','1','0,1','2','0.5,0.9')
colors_list = ('green','blue','yellow','cyan','magenta','pink')
اکنون، اینها را در قالب های فرعی a بسته بندی می کنیم Figure برای تجسم و تولید داده های مصنوعی مبتنی بر روی این توزیعها، پارامترها و رنگهای مناسب را به آنها اختصاص میدهند.
این کار از طریق eval() تابعی که از آن برای تولید عبارت پایتون استفاده می کنیم. به عنوان مثال می توانیم استفاده کنیم rand.exponential(1, 5000) برای تولید نمونه از توزیع نمایی مقیاس 1 و اندازه 5000.
در اینجا، ما از خود استفاده خواهیم کرد dist_list، param_list و color_list برای ایجاد این تماس ها:
fig,ax = plt.subplots(nrows=2, ncols=3,figsize=(12,7))
plt_ind_list = np.arange(6)+231
for dist, plt_ind, param, colors in zip(dist_list, plt_ind_list, param_list, colors_list):
x = eval('rand.'+dist+'('+param+',5000)')
plt.subplot(plt_ind)
plt.hist(x,bins=50,color=colors)
plt.title(dist)
fig.subplots_adjust(hspace=0.4,wspace=.3)
plt.suptitle('Sampling from Various Distributions',fontsize=20)
plt.show()
این منجر به:

داده های ترکیبی برای رگرسیون
را بسته sklearn.datasets دارای توابع برای تولید مجموعه داده های مصنوعی برای رگرسیون در اینجا، داده های خطی و غیر خطی را برای رگرسیون مورد بحث قرار می دهیم.
را make_regression() تابع مجموعه ای از نقاط داده ورودی (رگرسیون) را به همراه خروجی آنها (هدف) برمی گرداند. این تابع را می توان با پارامترهای زیر تنظیم کرد:
n_features– تعداد ابعاد/ویژگی های داده های تولید شدهnoise– انحراف استاندارد نویز گاوسیn_samples– تعداد نمونه ها
متغیر پاسخ ترکیبی خطی از مجموعه ورودی تولید شده است.
متغیر پاسخ چیزی است که وابسته است روی متغیرهای دیگر، در این مورد خاص، یک ویژگی هدف است که سعی می کنیم با استفاده از تمام ویژگی های ورودی دیگر آن را پیش بینی کنیم.
در کد زیر، داده های مصنوعی برای سطوح مختلف نویز تولید شده است و از دو ویژگی ورودی و یک متغیر هدف تشکیل شده است. تغییر رنگ نقاط ورودی، تغییر در مقدار هدف، مربوط به نقطه داده را نشان می دهد. داده ها برای تجسم بهتر به صورت دو بعدی تولید می شوند، اما داده های با ابعاد بالا را می توان با استفاده از آن ایجاد کرد n_features پارامتر:
map_colors = plt.cm.get_cmap('RdYlBu')
fig,ax = plt.subplots(nrows=2, ncols=3,figsize=(16,7))
plt_ind_list = np.arange(6)+231
for noise,plt_ind in zip((0,0.1,1,10,100,1000),plt_ind_list):
x,y = dt.make_regression(n_samples=1000,
n_features=2,
noise=noise,
random_state=rand_state)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x(:,0),
x(:,1),
c=y,
vmin=min(y),
vmax=max(y),
s=35,
cmap=color_map)
plt.title('noise: '+str(noise))
plt.colorbar(my_scatter_plot)
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_regression() With Different Noise Levels',fontsize=20)
plt.show()
در اینجا، ما مجموعه ای از 1000 نمونه، با دو متغیر ورودی (ویژگی) ایجاد کرده ایم. بسته به روی سطح سر و صدا (0..1000، می توانیم ببینیم که چگونه داده های تولید شده به طور قابل توجهی متفاوت است روی طرح پراکندگی:

را make_friedman خانواده توابع
سه نسخه از آن وجود دارد make_friedman?() تابع (جایگزین ? با مقدار از {1,2,3}).
این توابع متغیر هدف را با استفاده از ترکیب غیر خطی متغیرهای ورودی تولید می کنند که در زیر به تفصیل شرح داده شده است:
-
make_friedman1():n_featuresآرگومان این تابع باید حداقل 5 باشد، بنابراین حداقل تعداد 5 بعد ورودی ایجاد می شود. در اینجا هدف توسط:
$$
y(x) = 10 * \sin(\pi x_0 x_1) + 20(x_2 – 0.5)^2 + 10x_3 + 5x_4 + \text{نویز}
$$ -
make_friedman2(): داده های تولید شده دارای 4 بعد ورودی است. متغیر پاسخ به صورت زیر ارائه می شود:
$$
y(x) = \sqrt{(x_0^2+x_1 x_2 – \frac{1}{(x_1 x_3)^2})} + \text{نویز}
$$
make_friedman3(): داده های تولید شده در این حالت نیز دارای 4 بعد می باشد. متغیر خروجی به صورت زیر داده می شود:
$$
y(x) = \arctan(\frac{x_1 x_2 -\frac{1}{(x_1 x_3)}}{x_0})+\text{نویز}
$$
کد زیر مجموعه داده ها را با استفاده از این توابع تولید می کند و سه ویژگی اول را به صورت سه بعدی ترسیم می کند که رنگ ها بر اساس متغیر هدف متفاوت است:
fig = plt.figure(figsize=(18,5))
x,y = dt.make_friedman1(n_samples=1000,n_features=5,random_state=rand_state)
ax = fig.add_subplot(131, projection='3d')
my_scatter_plot = ax.scatter(x(:,0), x(:,1),x(:,2), c=y, cmap=color_map)
fig.colorbar(my_scatter_plot)
plt.title('make_friedman1')
x,y = dt.make_friedman2(n_samples=1000,random_state=rand_state)
ax = fig.add_subplot(132, projection='3d')
my_scatter_plot = ax.scatter(x(:,0), x(:,1),x(:,2), c=y, cmap=color_map)
fig.colorbar(my_scatter_plot)
plt.title('make_friedman2')
x,y = dt.make_friedman3(n_samples=1000,random_state=rand_state)
ax = fig.add_subplot(133, projection='3d')
my_scatter_plot = ax.scatter(x(:,0), x(:,1),x(:,2), c=y, cmap=color_map)
fig.colorbar(my_scatter_plot)
plt.suptitle('make_friedman?() for Non-Linear Data',fontsize=20)
plt.title('make_friedman3')
plt.show()

داده های مصنوعی برای طبقه بندی
Scikit- Learn دارای توابع ساده و آسان برای تولید مجموعه داده ها برای طبقه بندی در sklearn.dataset مدول. اجازه دهید چند مثال را مرور کنیم.
make_classification() برای مسائل طبقه بندی n-Class
برای مسائل طبقه بندی n کلاس، make_classification() تابع چندین گزینه دارد:
class_sep: مشخص می کند که آیا طبقات مختلف باید گسترده تر باشند و تشخیص آنها آسان تر باشدn_features: تعداد امکاناتn_redundant: تعداد ویژگی های اضافیn_repeated: تعداد ویژگی های تکراریn_classes: تعداد کل کلاس ها
بیایید یک مجموعه داده طبقه بندی برای داده های ورودی دو بعدی بسازیم. ما ارزش های متفاوتی خواهیم داشت class_sep برای یک مشکل طبقه بندی باینری نقاط رنگی یکسان متعلق به یک کلاس هستند. شایان ذکر است که این تابع همچنین می تواند کلاس های نامتعادل ایجاد کند:
fig,ax = plt.subplots(nrows=1, ncols=3,figsize=(16,5))
plt_ind_list = np.arange(3)+131
for class_sep,plt_ind in zip((0.1,1,10),plt_ind_list):
x,y = dt.make_classification(n_samples=1000,
n_features=2,
n_repeated=0,
class_sep=class_sep,
n_redundant=0,
random_state=rand_state)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x(:,0),
x(:,1),
c=y,
vmin=min(y),
vmax=max(y),
s=35,
cmap=color_map_discrete)
plt.title('class_sep: '+str(class_sep))
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_classification() With Different class_sep Values',fontsize=20)
plt.show()

make_multilabel_classification() برای مسائل طبقه بندی چند برچسبی
make_multilabel_classification() تابع داده هایی را برای مسائل طبقه بندی چند برچسبی تولید می کند. گزینه های مختلفی دارد که قابل توجه ترین آنهاست n_label، که میانگین تعداد برچسب ها را در هر نقطه داده تعیین می کند.
بیایید یک مشکل چند برچسبی 4 کلاسه را در نظر بگیریم، با بردار هدف برچسب ها که برای تجسم به یک مقدار تبدیل می شود. نقاط با توجه به نمایش اعشاری بردار برچسب باینری رنگ می شوند. کد به شما کمک می کند تا ببینید که چگونه از یک مقدار متفاوت برای استفاده می کنید n_label، طبقه بندی یک نقطه داده تولید شده را تغییر می دهد:
fig,ax = plt.subplots(nrows=1, ncols=3,figsize=(16,5))
plt_ind_list = np.arange(3)+131
for label,plt_ind in zip((2,3,4),plt_ind_list):
x,y = dt.make_multilabel_classification(n_samples=1000,
n_features=2,
n_labels=label,
n_classes=4,
random_state=rand_state)
target = np.sum(y*(8,4,2,1),axis=1)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x(:,0),
x(:,1),
c=target,
vmin=min(target),
vmax=max(target),
cmap=color_map)
plt.title('n_labels: '+str(label))
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_multilabel_classification() With Different n_labels Values',fontsize=20)
plt.show()

داده های ترکیبی برای خوشه بندی
برای خوشه بندی، sklearn.datasets چندین گزینه ارائه می دهد. در اینجا، ما را پوشش خواهیم داد make_blobs() و make_circles() کارکرد.
make_blobs()
را make_blobs() تابع داده ها را از توزیع های گاوسی همسانگرد تولید می کند. تعداد ویژگی ها، تعداد مراکز و انحراف استاندارد هر خوشه را می توان به عنوان یک آرگومان مشخص کرد.
در اینجا، این تابع را به صورت دو بعدی نشان می دهیم و نشان می دهیم که چگونه نقاط داده با مقادیر مختلف تغییر می کنند cluster_std پارامتر:
fig,ax = plt.subplots(nrows=1, ncols=3,figsize=(16,5))
plt_ind_list = np.arange(3)+131
for std,plt_ind in zip((0.5,1,10),plt_ind_list):
x, label = dt.make_blobs(n_features=2,
centers=4,
cluster_std=std,
random_state=rand_state)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x(:,0),
x(:,1),
c=label,
vmin=min(label),
vmax=max(label),
cmap=color_map_discrete)
plt.title('cluster_std: '+str(std))
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_blobs() With Different cluster_std Values',fontsize=20)
plt.show()

make_circles()
را make_circles() تابع دو دایره متحدالمرکز با مرکز یکسان، یکی در داخل دیگری ایجاد می کند.
با استفاده از پارامتر نویز می توان اعوجاج را به داده های تولید شده اضافه کرد. این نوع داده برای ارزیابی الگوریتمهای خوشهبندی مبتنی بر قرابت مفید است. کد زیر داده های مصنوعی تولید شده در سطوح مختلف نویز را نشان می دهد:
fig,ax = plt.subplots(nrows=1, ncols=3,figsize=(16,5))
plt_ind_list = np.arange(3)+131
for noise,plt_ind in zip((0,0.1,1),plt_ind_list):
x, label = dt.make_circles(noise=noise,random_state=rand_state)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x(:,0),
x(:,1),
c=label,
vmin=min(label),
vmax=max(label),
cmap=color_map_discrete)
plt.title('noise: '+str(noise))
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_circles() With Different Noise Levels',fontsize=20)
plt.show()

تولید نمونه های مشتق شده از مجموعه داده های ورودی
راههای زیادی برای تولید نمونههای داده اضافی از یک مجموعه داده موجود وجود دارد. در اینجا، ما یک روش بسیار ساده را نشان می دهیم که ابتدا چگالی هسته داده ها را با استفاده از یک هسته گاوسی تخمین می زند و سپس نمونه های اضافی را از این توزیع تولید می کند.
برای تجسم نمونه های تازه تولید شده، اجازه دهید به مجموعه داده چهره های Olivetti، قابل بازیابی از طریق نگاه کنیم. sklearn.datasets.fetch_olivetti_faces(). مجموعه داده دارای 10 تصویر مختلف از چهره 40 فرد مختلف است.
این چیزی است که ما انجام خواهیم داد:
- داده های چهره را دریافت کنید
- مدل چگالی هسته را از داده ها ایجاد کنید
- از چگالی هسته برای تولید نمونه های جدید داده استفاده کنید
- نمایش چهره های اصلی و مصنوعی.
faces = dt.fetch_olivetti_faces()
X = faces.data
bandwidth_params = {'bandwidth': np.arange(0.01,1,0.05)}
grid_search = GridSearchCV(KernelDensity(), bandwidth_params)
grid_search.fit(X)
kde = grid_search.best_estimator_
new_faces = kde.sample(8, random_state=rand_state)
fig,ax = plt.subplots(nrows=2, ncols=8,figsize=(18,6),subplot_kw=dict(xticks=(), yticks=()))
for i in np.arange(8):
ax(0,i).imshow(X(10*i,:).reshape(64,64),cmap=plt.cm.gray)
ax(1,i).imshow(new_faces(i,:).reshape(64,64),cmap=plt.cm.gray)
ax(0,3).set_title('Original Data',fontsize=20)
ax(1,3).set_title('Synthetic Data',fontsize=20)
fig.subplots_adjust(wspace=.1)
plt.show()

چهرههای اصلی که در اینجا نشان داده شدهاند نمونهای از 8 چهره هستند که از بین 400 تصویر انتخاب شدهاند تا ایدهای در مورد اینکه مجموعه داده اصلی چگونه است. ما میتوانیم با استفاده از آن هر تعداد نقطه داده جدید تولید کنیم sample() تابع.
در این مثال 8 نمونه جدید تولید شد. توجه داشته باشید که چهره های مصنوعی نشان داده شده در اینجا لزوماً با چهره شخصی که در بالای آن نشان داده شده است مطابقت ندارد.
نتیجه گیری
در این مقاله با چند روش تولید مجموعه داده مصنوعی برای مشکلات مختلف آشنا شدیم. مجموعه دادههای مصنوعی به ما کمک میکنند الگوریتمهای خود را تحت شرایط کنترلشده ارزیابی کنیم و یک خط پایه برای معیارهای عملکرد تعیین کنیم.
پایتون دارای طیف گسترده ای از توابع است که می تواند برای تولید داده های مصنوعی استفاده شود. درک اینکه کدام توابع و APIها می توانند برای نیازهای خاص شما استفاده شوند بسیار مهم است.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-15 22:16:03



