از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
مرتب سازی حبابی در پایتون
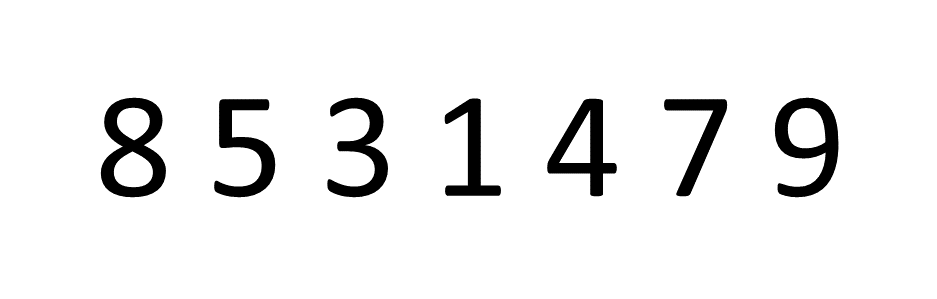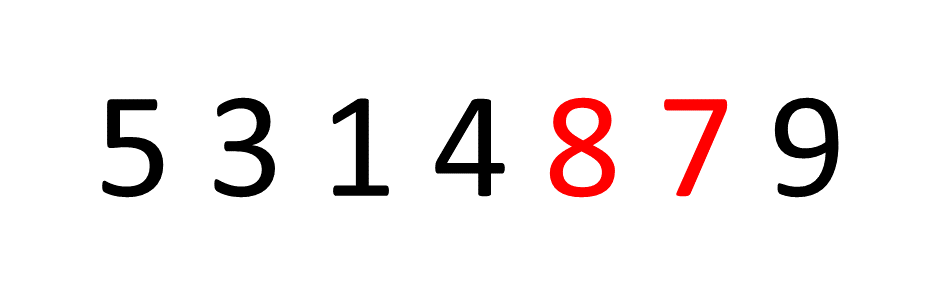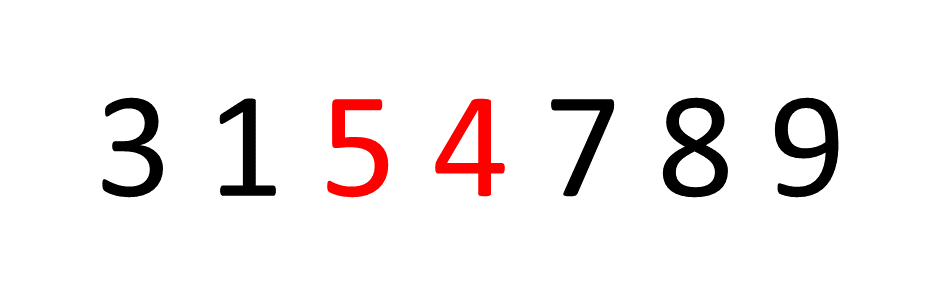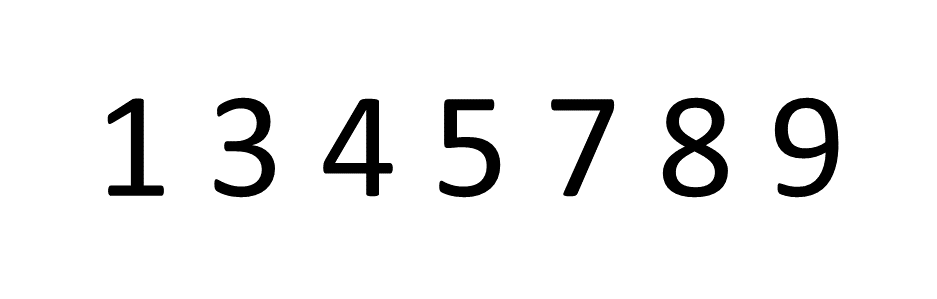
سرفصلهای مطلب
معرفی
برای اکثر مردم، مرتبسازی حبابها احتمالاً اولین الگوریتم مرتبسازی است که در درس علوم رایانهشان شنیدهاند.
“ترجمه” آن به کد بسیار شهودی و آسان است، که برای توسعه دهندگان نرم افزار جدید مهم است تا بتوانند ایده ها را به شکلی قابل اجرا تبدیل کنند. روی یک کامپیوتر. با این حال، Bubble Sort یکی از این موارد است بدترین عملکرد الگوریتم های مرتب سازی در همه موارد به جز بررسی اینکه آیا آرایه از قبل مرتب شده است یا خیر، جایی که اغلب از الگوریتم های مرتب سازی کارآمدتر مانند مرتب سازی سریع بهتر عمل می کند.
ایده پشت مرتب سازی حباب
ایده پشت مرتب سازی حباب بسیار ساده است، ما به جفت عناصر مجاور در یک آرایه، یک جفت در یک زمان، و swap موقعیت آنها اگر عنصر اول بزرگتر از عنصر دوم باشد یا به سادگی حرکت کنند روی اگر اینطور نیست بیایید به یک مثال نگاه کنیم و آرایه را مرتب کنیم (8, 5, 3, 1, 4, 7, 9):

اگر تمرکز کنید روی عدد اول، عدد 8، می توانید ببینید که آرایه را در جای درست “حباب” می کند. سپس، این process برای تعداد تکرار می شود 5 و غیره روی.
روش پیاده سازی مرتب سازی حباب در پایتون
با خارج شدن از تجسم، بیایید جلو برویم و الگوریتم را پیاده سازی کنیم. باز هم، بسیار ساده است:
def bubble_sort(our_list):
for i in range(len(our_list)):
for j in range(len(our_list) - 1):
if our_list(j) > our_list(j+1):
our_list(j), our_list(j+1) = our_list(j+1), our_list(j)
حالا بیایید لیستی را پر کنیم و الگوریتم را فراخوانی کنیم روی آی تی:
our_list = (19, 13, 6, 2, 18, 8)
bubble_sort(our_list)
print(our_list)
این به ما می دهد:
(2, 6, 8, 13, 18, 19)
بهینه سازی
پیاده سازی ساده کار خود را انجام داد، اما دو بهینه سازی وجود دارد که می توانیم در اینجا انجام دهیم.
وقتی هیچ مبادله ای انجام نمی شود، به این معنی است که لیست مرتب شده است. با این حال، با الگوریتمی که قبلاً اجرا شده بود، به ارزیابی بقیه لیست ادامه میدهد، حتی اگر واقعاً نیازی به این کار نباشد. برای رفع این مشکل، یک را نگه می داریم boolean پرچم گذاری کنید و بررسی کنید که آیا تعویض در تکرار قبلی انجام شده است یا خیر.
اگر مبادله ای انجام نشود، الگوریتم باید متوقف شود:
def bubble_sort(our_list):
has_swapped = True
while(has_swapped):
has_swapped = False
for i in range(len(our_list) - 1):
if our_list(i) > our_list(i+1):
our_list(i), our_list(i+1) = our_list(i+1), our_list(i)
has_swapped = True
بهینهسازی دیگری که میتوانیم انجام دهیم این واقعیت را تحت تأثیر قرار میدهد که مرتبسازی حبابی بهگونهای کار میکند که بزرگترین عناصر در یک تکرار خاص به انتهای آرایه ختم میشوند.
اولین باری که از لیست موقعیت عبور می کنیم n تضمین شده است که بزرگترین عنصر است، دومین بار که از موقعیت عبور می کنیم n-1 تضمین شده است که دومین عنصر بزرگ است، و غیره.
این بدان معنی است که با هر تکرار متوالی می توانیم به یک عنصر کمتر از قبل نگاه کنیم. به طور دقیق تر، در کتکرار -ام، فقط باید به اولین نگاه کنید n – k + 1 عناصر:
def bubble_sort(our_list):
has_swapped = True
num_of_iterations = 0
while(has_swapped):
has_swapped = False
for i in range(len(our_list) - num_of_iterations - 1):
if our_list(i) > our_list(i+1):
our_list(i), our_list(i+1) = our_list(i+1), our_list(i)
has_swapped = True
num_of_iterations += 1
مرتب سازی حباب بهینه در مقابل غیر بهینه شده
بیایید جلوتر برویم و زمان لازم برای مرتب کردن هر یک از این کدها را برای مرتب کردن یک لیست هزار بار با استفاده از timeit مدول:
Unoptimized Bubble Sort took: 0.0106407
Bubble Sort with a boolean flag took: 0.0078251
Bubble Sort with a boolean flag and shortened list took: 0.0075207
تفاوت زیادی بین دو رویکرد اخیر وجود ندارد، زیرا لیست بسیار کوتاه است، اما روی لیست های بزرگتر – بهینه سازی دوم می تواند تفاوت بزرگی ایجاد کند.
نتیجه
در ناکارآمدترین رویکرد، مرتبسازی حبابها انجام میشود n-1 تکرارها، نگاه کردن به n-1 جفت عناصر مجاور این به آن پیچیدگی زمانی \)O(n^2)\) را در هر دو شرایط بهترین و متوسط می دهد. \)O(n^2)\) برای یک الگوریتم مرتب سازی بسیار وحشتناک در نظر گرفته می شود.
یک دارد O (1) پیچیدگی فضا، اما این برای جبران کاستی های آن در زمینه های دیگر کافی نیست.
با این حال، هنوز هم بخش بزرگی از جامعه توسعه نرمافزار و تاریخ است، و کتابهای درسی تقریباً هرگز از ذکر آن در مورد الگوریتمهای مرتبسازی اولیه کوتاهی نمیکنند.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-18 05:31:03



