مرتب سازی هیپ در پایتون

معرفی

مرتب سازی پشته نمونه دیگری از یک الگوریتم مرتب سازی کارآمد است. مزیت اصلی آن این است که بدون در نظر گرفتن داده های ورودی، زمان اجرای بسیار خوبی در بدترین حالت \(O(nlogn)\) دارد.

همانطور که از نام آن پیداست، Heap Sort به شدت متکی است روی را پشته ساختار داده – اجرای مشترک الف صف اولویت.

بدون شک Heap Sort یکی از ساده‌ترین الگوریتم‌های مرتب‌سازی برای پیاده‌سازی است، و همراه با این واقعیت که یک الگوریتم نسبتاً کارآمد در مقایسه با سایر پیاده‌سازی‌های ساده است، یک الگوریتم معمولی است.

ایده پشت دسته بندی

مرتب سازی هیپ با حذف عناصر از قسمت پشته آرایه یکی یکی و اضافه کردن آنها به قسمت مرتب شده آرایه کار می کند. قبل از اینکه به توضیح بیشتر بپردازیم و ساختار داده های پشته را دوباره بررسی کنیم، باید به چند ویژگی خود مرتب سازی هیپ اشاره کنیم.

یک است درجا الگوریتم، به این معنی که به مقدار ثابتی از حافظه اضافی نیاز دارد، یعنی حافظه مورد نیاز بستگی ندارد روی اندازه خود آرایه اولیه، غیر از حافظه مورد نیاز برای ذخیره آن آرایه.

برای مثال، هیچ کپی از آرایه اصلی لازم نیست، و هیچ پشته تماس بازگشتی و بازگشتی وجود ندارد. ساده‌ترین پیاده‌سازی Heap Sort معمولاً از یک آرایه دوم برای ذخیره مقادیر مرتب‌شده استفاده می‌کند. ما از این روش استفاده خواهیم کرد زیرا در کد بسیار بصری تر و آسان تر است، اما می توان آن را به طور کامل پیاده سازی کرد. درجا.

مرتب سازی هیپ است ناپایدار، به این معنی که ترتیب نسبی عناصر با مقادیر برابر را حفظ نمی کند. این یک مشکل با انواع اولیه (مانند اعداد صحیح و کاراکترها…) نیست، اما زمانی که انواع پیچیده مانند اشیا را مرتب می کنیم، می تواند مشکل ساز شود.

به عنوان مثال، تصور کنید یک کلاس سفارشی داریم Person با age و name فیلدها، و چندین شی از آن کلاس در یک آرایه، از جمله شخصی به نام “Mike” 19 ساله، و “David”، همچنین 19 ساله – که به ترتیب ظاهر می شوند.

اگر تصمیم بگیریم آن آرایه از افراد را بر اساس سن مرتب کنیم، هیچ تضمینی وجود نخواهد داشت که “مایک” قبل از “دیوید” در آرایه مرتب شده ظاهر شود، حتی اگر آنها به ترتیب در آرایه اولیه ظاهر شوند. آی تی می توان اتفاق می افتد، اما تضمین نشده است.

ساختار داده هیپ

Heaps یکی از محبوب‌ترین و پرکاربردترین ساختارهای داده در علوم کامپیوتر است – البته در مصاحبه‌های مهندسی نرم‌افزار بسیار محبوب است.

ما در مورد پشته ها صحبت خواهیم کرد که کوچکترین عنصر (min-heap) را دنبال می کنند، اما آنها می توانند به همین راحتی برای پیگیری بزرگترین عنصر (max-heap) پیاده سازی شوند.

به زبان ساده، الف min-heap یک ساختار داده مبتنی بر درخت است که در آن هر node از همه فرزندانش کوچکتر است اغلب از درخت باینری استفاده می شود. Heaps دارای سه عملیات پشتیبانی شده است – delete_minimum()، get_minimum()، و add().

تو می توانی فقط اولین عنصر در پشته را حذف کنید، پس از آن “دوباره مرتب می شود”. پشته ها پس از افزودن یا حذف یک عنصر، خود را مجدداً مرتب می کنند تا کوچکترین عنصر همیشه در موقعیت اول قرار گیرد.

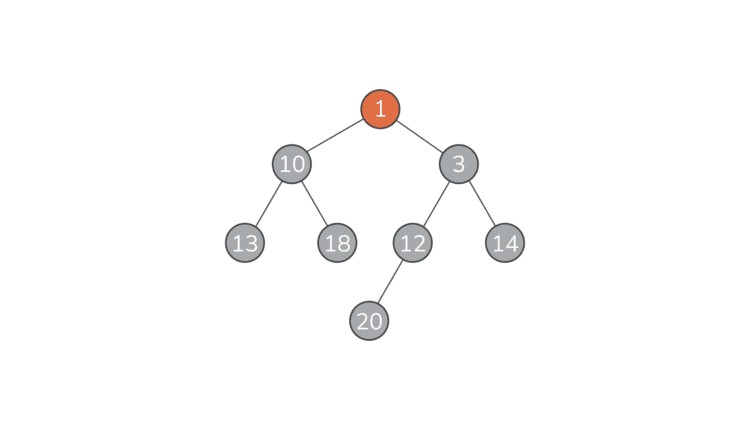
بیایید به مثالی از یک پشته نگاه کنیم:

همانطور که می بینیم، مثال بالا با توصیف یک پشته مطابقت دارد اما مرتب نشده است. ما به جزئیات اجرای heap نمی پردازیم زیرا تمرکز این مقاله نیست. مزیت مهم ساختار داده هپ که هنگام استفاده از آن در مرتب سازی هیپ استفاده می کنیم این است که بعدی کوچکترین عنصر همیشه اولین عنصر در پشته است.

روش پیاده سازی مرتب سازی هیپ در پایتون

مرتب سازی آرایه ها

پایتون روش هایی را برای ایجاد و استفاده از پشته ها ارائه می دهد تا مجبور نباشیم خودمان آنها را پیاده سازی کنیم:

• heappush(list, item) – یک عنصر را به پشته اضافه می کند و پس از آن دوباره آن را مرتب می کند تا یک پشته باقی بماند. می تواند به کار رود روی یک لیست خالی
• heappop(list) – اولین (کوچکترین) عنصر را پاپ می کند (حذف می کند) و آن عنصر را برمی گرداند. پشته پس از این عملیات به صورت پشته باقی می ماند، بنابراین نیازی به تماس نیست heapify().
• heapify(list) – لیست داده شده را به یک پشته تبدیل می کند. شایان ذکر است که این روش وجود دارد حتی اگر ما از آن استفاده نخواهیم کرد زیرا نمی خواهیم آرایه اصلی خود را تغییر دهیم.

اکنون که این را می دانیم، پیاده سازی Heap Sort نسبتاً ساده است:

from heapq import heappop, heappush

def heap_sort(array):
    heap = ()
    for element in array:
        heappush(heap, element)

    ordered = ()

    
    while heap:
        ordered.append(heappop(heap))

    return ordered

array = (13, 21, 15, 5, 26, 4, 17, 18, 24, 2)
print(heap_sort(array))

خروجی:

(2, 4, 5, 13, 15, 17, 18, 21, 24, 26)

همانطور که می بینیم، عملیات سنگین کردن با ساختار داده های پشته انجام می شود، تنها کاری که باید انجام دهیم این است که تمام عناصر مورد نیاز خود را اضافه کرده و آنها را یکی یکی حذف کنیم. این تقریباً مانند یک دستگاه سکه‌شمار است که سکه‌های ورودی را بر اساس ارزششان مرتب می‌کند و ما می‌توانیم آنها را بعد از آن خارج کنیم.

مرتب سازی اشیاء سفارشی

هنگام استفاده از کلاس های سفارشی همه چیز کمی پیچیده تر می شود. معمولاً به منظور استفاده از الگوریتم‌های مرتب‌سازی خود در کلاس‌ها، توصیه می‌کنیم که عملگرهای مقایسه را نادیده نگیریم و در عوض پیشنهاد می‌کنیم الگوریتم را بازنویسی کنیم تا به جای آن یک مقایسه‌کننده تابع لامبدا بگیرد.

با این حال، از آنجایی که اجرای ما متکی است روی روش های پشته داخلی، ما نمی توانیم این کار را در اینجا انجام دهیم.

پایتون متدهای زیر را ارائه می کند:

• heapq.nlargest(*n*, *iterable*, *key=None*) – فهرستی را با n بزرگترین عناصر از مجموعه داده تعریف شده توسط iterable.
• heapq.nsmallest(*n*, *iterable*, *key=None*) – فهرستی را با n کوچکترین عناصر از مجموعه داده تعریف شده توسط iterable.

ما می توانیم از آن برای به دست آوردن ساده استفاده کنیم n = len(array) بزرگترین/کوچکترین عناصر اما خود روش ها از مرتب سازی هیپ استفاده نمی کنند و اساساً معادل فراخوانی sorted() روش.

تنها راه حلی که برای کلاس‌های سفارشی باقی می‌ماند، لغو عملگرهای مقایسه است. این متأسفانه ما را محدود می کند فقط یک نوع مقایسه در هر کلاس. در مثال ما، ما را به مرتب سازی محدود می کند Movie اشیاء بر اساس سال

با این حال، به ما اجازه می دهد تا با استفاده از مرتب سازی هیپ نشان دهیم روی کلاس های سفارشی بیایید جلو برویم و آن را تعریف کنیم Movie کلاس:

from heapq import heappop, heappush

class Movie:
    def __init__(self, title, year):
        self.title = title
        self.year = year

    def __str__(self):
        return str.format("Title: {}, Year: {}", self.title, self.year)

    def __lt__(self, other):
        return self.year < other.year

    def __gt__(self, other):
        return other.__lt__(self)

    def __eq__(self, other):
        return self.year == other.year

    def __ne__(self, other):
        return not self.__eq__(other)

و اکنون، اجازه دهید کمی خود را اصلاح کنیم heap_sort() تابع:

def heap_sort(array):
    heap = ()
    for element in array:
        heappush(heap, element)

    ordered = ()

    while heap:
        ordered.append(heappop(heap))

    return ordered

و در نهایت، اجازه دهید چند فیلم را نمونه برداری کنیم، آنها را در یک آرایه قرار دهیم و سپس آنها را مرتب کنیم:

movie1 = Movie("Citizen Kane", 1941)
movie2 = Movie("Back to the Future", 1985)
movie3 = Movie("Forrest Gump", 1994)
movie4 = Movie("The Silence of the Lambs", 1991);
movie5 = Movie("Gia", 1998)

array = (movie1, movie2, movie3, movie4, movie5)

for movie in heap_sort(array):
    print(movie)

خروجی:

Title: Citizen Kane, Year: 1941
Title: Back to the Future, Year: 1985
Title: The Silence of the Lambs, Year: 1991
Title: Forrest Gump, Year: 1994
Title: Gia, Year: 1998

مقایسه با سایر الگوریتم های مرتب سازی

یکی از دلایل اصلی اینکه مرتب‌سازی Heap هنوز هم اغلب استفاده می‌شود، حتی اگر مرتب‌سازی سریع به خوبی اجرا شده از آن بهتر عمل کند، قابلیت اطمینان آن است.

مزیت اصلی Heap Sort در اینجا حد بالایی \(O(nlogn)\) از نظر پیچیدگی زمانی و نگرانی های امنیتی است. توسعه دهندگان هسته لینوکس دلایل زیر را برای استفاده از مرتب سازی هیپ بر روی مرتب سازی سریع بیان می کنند:

زمان مرتب‌سازی Heap Sort \(O(nlogn)\) هر دو است روی متوسط ​​و بدترین حالت در حالی که qsort حدود 20٪ سریعتر است روی به طور متوسط، از رفتار قابل بهره برداری \(O(n^2)\) در بدترین حالت و نیازهای حافظه اضافی رنج می برد که آن را برای استفاده از هسته کمتر مناسب می کند.

علاوه بر این، مرتب‌سازی سریع در موقعیت‌های قابل پیش‌بینی ضعیف عمل می‌کند، و با توجه به دانش کافی از پیاده‌سازی داخلی، می‌تواند یک خطر امنیتی (عمدتا حملات DDoS) ایجاد کند زیرا رفتار بد \(O(n^2)\) به راحتی می‌تواند فعال شود.

الگوریتم دیگری که مرتب سازی هیپ اغلب با آن مقایسه می شود، مرتب سازی ادغام است که پیچیدگی زمانی یکسانی دارد.

Merge Sort مزیت بودن را دارد پایدار و به طور شهودی قابل موازی سازی، در حالی که مرتب سازی هیپ هیچ کدام نیست.

نکته دیگر این است که مرتب‌سازی هیپ در بیشتر موارد کندتر از مرتب‌سازی ادغام است، حتی اگر پیچیدگی یکسانی داشته باشند زیرا مرتب‌سازی هپ فاکتورهای ثابت بزرگ‌تری دارد.

با این حال، مرتب‌سازی هیپ می‌تواند بسیار راحت‌تر اجرا شود درجا از ادغام مرتب سازی می تواند، بنابراین ترجیح داده می شود زمانی که حافظه عامل مهمتر از سرعت است.

نتیجه

همانطور که دیدیم، Heap Sort به اندازه سایر الگوریتم های کارآمد و همه منظوره محبوب نیست، اما رفتار قابل پیش بینی آن (به غیر از ناپایدار بودن) آن را به یک الگوریتم عالی برای استفاده در مواردی که حافظه و امنیت مهمتر از زمان اجرای کمی سریعتر هستند تبدیل می کند.

پیاده سازی و استفاده از عملکرد داخلی ارائه شده با پایتون واقعاً شهودی است، تنها کاری که ما اساساً باید انجام دهیم این است که موارد را در یک پشته قرار داده و آنها را بیرون بیاوریم – مشابه یک شمارنده سکه.