از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
مقدمه ای بر یادگیری تقویتی با پایتون
سرفصلهای مطلب
معرفی
یادگیری تقویتی قطعا یکی از فعال ترین و محرک ترین زمینه های تحقیق در هوش مصنوعی است.
علاقه به این زمینه در طی چند سال گذشته، به دنبال پیشرفتهای بزرگ (و تبلیغاتی بسیار) مانند DeepMind’s AlphaGo شکست دادن کلمه قهرمان مدل های GO و OpenAI AI شکست دادن بازیکنان حرفه ای DOTA.
به لطف همه این پیشرفتها، یادگیری تقویتی در حال حاضر در زمینههای مختلف، از مراقبتهای بهداشتی تا مالی، از شیمی تا مدیریت منابع، استفاده میشود.
در این مقاله به معرفی مفاهیم و اصطلاحات اساسی یادگیری تقویتی می پردازیم و آنها را در یک مثال کاربردی به کار می بریم.
یادگیری تقویتی چیست؟
یادگیری تقویتی (RL) شاخه ای از یادگیری ماشینی است که با بازیگران یا عوامل، انجام اقدامات نوعی است محیط به منظور به حداکثر رساندن نوعی از جایزه که در طول مسیر جمع آوری می کنند.
این به عمد یک تعریف بسیار سست است، به همین دلیل است که تکنیک های یادگیری تقویتی را می توان برای طیف بسیار گسترده ای از مسائل دنیای واقعی به کار برد.
تصور کنید شخصی در حال انجام یک بازی ویدیویی است. بازیکن عامل است و بازی محیط است. پاداش هایی که بازیکن دریافت می کند (یعنی شکست دادن یک دشمن، تکمیل یک سطح)، یا نمی کند get (به عنوان مثال وارد یک تله، شکست در یک مبارزه) به او می آموزد که چگونه بازیکن بهتری باشد.
همانطور که احتمالا متوجه شده اید، یادگیری تقویتی واقعاً در مقوله های یادگیری تحت نظارت/بدون نظارت/نیمه نظارت قرار نمی گیرد.
به عنوان مثال، در یادگیری نظارت شده، هر تصمیمی که توسط مدل گرفته می شود مستقل است و بر آنچه در آینده می بینیم تأثیر نمی گذارد.
در عوض، در یادگیری تقویتی، ما به یک استراتژی بلندمدت برای عامل خود علاقه مندیم، که ممکن است شامل تصمیمات غیربهینه در مراحل میانی و یک مبادله بین اکتشاف (از مسیرهای ناشناخته)، و بهره برداری از آنچه قبلاً در مورد محیط زیست می دانیم.
تاریخچه مختصر یادگیری تقویتی
برای چندین دهه (از دهه 1950!)، یادگیری تقویتی دو رشته تحقیقاتی جداگانه را دنبال کرد، یکی با تمرکز روی ازمایش و خطا رویکردها، و یک مبتنی بر روی کنترل بهینه.
هدف روش های کنترل بهینه طراحی یک کنترل کننده برای به حداقل رساندن اندازه گیری رفتار یک سیستم دینامیکی در طول زمان است. برای رسیدن به این هدف، آنها عمدتاً از الگوریتم های برنامه نویسی پویا استفاده کردند که خواهیم دید که پایه های تکنیک های یادگیری تقویتی مدرن هستند.
رویکردهای آزمون و خطا، در عوض، ریشه های عمیقی در روانشناسی یادگیری حیوانات و علوم اعصاب دارند، و اینجاست که اصطلاح تقویت ناشی از: اقدامات به دنبال (تقویت شده) با نتایج خوب یا بد تمایل به انتخاب مجدد بر این اساس دارند.
برخاسته از مطالعه میان رشته ای این دو رشته، رشته ای به نام یادگیری تفاوت زمانی (TD)..
رویکردهای یادگیری ماشین مدرن به RL عمدتا مبتنی است روی TD-Learning، که با سیگنالهای پاداش و تابع ارزش سروکار دارد (در پاراگرافهای بعدی جزئیات بیشتری را مشاهده خواهیم کرد).
واژه شناسی
اکنون نگاهی به مفاهیم و اصطلاحات اصلی یادگیری تقویتی خواهیم داشت.
عامل
سیستمی که در یک محیط تعبیه شده و اقداماتی را برای تغییر وضعیت محیط انجام می دهد. به عنوان مثال می توان به روبات های متحرک، عوامل نرم افزاری یا کنترل کننده های صنعتی اشاره کرد.
محیط
سیستم بیرونی که عامل می تواند «درک» و عمل کند روی.
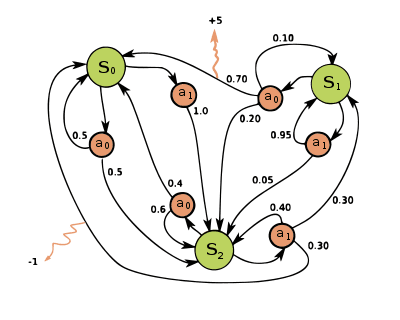
محیط ها در RL به عنوان فرآیندهای تصمیم گیری مارکوف (MDP) تعریف می شوند. MDP یک تاپل است:
$$
(S، A، P، R، \gamma)
$$
جایی که:
- اس مجموعه ای محدود از حالات است
- آ مجموعه محدودی از اقدامات است
- پ یک ماتریس احتمال انتقال حالت است
$$ P_{ss’}^{a} = \mathbb{P}(S_{t+1} = s’| S_t = s، A_t = a) $$
$$ R_s^a = \mathbb{E}(R_{t+1}|S_t=s، A_t = a) $$
- γ یک عامل تخفیف است، γ ∈ (0,1)

بسیاری از سناریوهای دنیای واقعی را می توان به صورت نمایش داد فرآیندهای تصمیم گیری مارکوف، از یک صفحه شطرنج ساده تا یک بازی ویدیویی بسیار پیچیده تر.
در یک محیط شطرنج، حالت ها همه پیکربندی های ممکن صفحه هستند (تعداد زیادی وجود دارد). اعمال به حرکت دادن مهره ها، تسلیم شدن و غیره اشاره دارد.
پاداش ها بر اساس آن است روی چه برنده باشیم یا چه ببازیم، به طوری که اقدامات برنده بازدهی بالاتری نسبت به باخت دارند.
احتمالات انتقال حالت قواعد بازی را اجرا می کنند. به عنوان مثال، یک عمل غیرقانونی (حرکت یک رخ به صورت مورب) احتمال صفر خواهد داشت.
تابع پاداش
تابع پاداش وضعیت ها را به پاداش های آنها نشان می دهد. این اطلاعاتی است که عوامل برای یادگیری روش حرکت در محیط استفاده می کنند.
تحقیقات زیادی برای طراحی یک تابع پاداش خوب و غلبه بر مشکل انجام می شود پاداش های اندک، زمانی که ماهیت اغلب پراکنده پاداش ها در محیط به عامل اجازه نمی دهد که به درستی از آن بیاموزد.
برگشت جیتی به عنوان مجموع تخفیف پاداش از مرحله زمانی تعریف می شود تی.
$$ G_t=\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} $$
γ عامل تخفیف نامیده می شود و با کاهش مقدار پاداش ها در حالی که به سمت آینده حرکت می کنیم، کار می کند.
تخفیف پاداش ها به ما امکان می دهد عدم اطمینان در مورد آینده را نشان دهیم، اما همچنین به ما کمک می کند رفتار انسانی را بهتر مدل کنیم، زیرا نشان داده شده است که انسان/حیوان برای پاداش های فوری ترجیح می دهند.
تابع ارزش
تابع مقدار احتمالاً مهم ترین اطلاعاتی است که می توانیم در مورد یک مشکل RL نگه داریم.
به طور رسمی، تابع مقدار است بازده مورد انتظار با شروع از حالت s. در عمل، تابع ارزش به ما می گوید که چقدر خوب است که عامل در یک وضعیت خاص باشد. هر چه ارزش یک حالت بالاتر باشد، میزان پاداشی که می توانیم انتظار داشته باشیم بیشتر است:
$$ v_\pi (s) = \mathbb{E}_\pi (G_t|S_t = s) $$
نام واقعی این تابع است ارزش دولتی تابع، برای متمایز کردن آن از یک عنصر مهم دیگر در RL: the عمل-ارزش تابع.
تابع action-value مقدار، یعنی بازگشت مورد انتظار را برای استفاده از action به ما می دهد آ در یک حالت خاص س:
$$ q_\pi (s, a) = \mathbb{E}_\pi (G_t|S_t = s، A_t = a) $$
خط مشی
این خط مشی رفتار نماینده ما را در MDP تعریف می کند.
به طور رسمی، سیاست ها هستند توزیع بر روی اقدامات در حالات داده شده. یک سیاست به احتمال انجام هر اقدام از آن حالت حالت ها را نشان می دهد:
$$ \pi (a|s) = \mathbb{P}(A_t = a|S_t=s) $$
هدف نهایی RL یافتن یک خط مشی بهینه (یا به اندازه کافی خوب) برای نماینده ما است. در مثال بازی ویدیویی، میتوانید خطمشی را بهعنوان استراتژیای که بازیکن دنبال میکند در نظر بگیرید، یعنی اقداماتی که بازیکن در صورت ارائه سناریوهای خاص انجام میدهد.
رویکردهای اصلی
مدلها و الگوریتمهای مختلفی برای مسائل RL اعمال میشوند.
واقعا، زیاد.
با این حال، همه آنها کم و بیش در دو دسته قرار می گیرند: مبتنی بر سیاست، و مبتنی بر ارزش.
رویکرد مبتنی بر سیاست
در رویکردهای مبتنی بر سیاست به RL، هدف ما یادگیری بهترین خط مشی ممکن است. مدلهای خطمشی مستقیماً بهترین حرکت ممکن را از وضعیت فعلی یا توزیع بر روی اقدامات ممکن بهدست میآورند.
رویکرد ارزش محور
در رویکردهای مبتنی بر ارزش، ما میخواهیم تابع مقدار بهینه را پیدا کنیم که تابع مقدار حداکثر بر روی همه سیاستها است.
سپس میتوانیم بر اساس اقداماتی که انجام دهیم (یعنی از کدام خطمشی استفاده کنیم) انتخاب کنیم روی مقادیری که از مدل دریافت می کنیم.
اکتشاف در مقابل بهره برداری
داد و ستد بین اکتشاف و بهره برداری به طور گسترده در ادبیات RL مورد مطالعه قرار گرفته است.
کاوش به عمل بازدید و جمعآوری اطلاعات در مورد وضعیتهایی در محیطی گفته میشود که هنوز از آنها بازدید نکردهایم یا هنوز اطلاعات زیادی درباره آنها نداریم. ایده این است که بررسی MDP ما ممکن است ما را به تصمیمات بهتر در آینده هدایت کند.
از طرف دیگر، بهره برداری شامل گرفتن بهترین تصمیم با توجه به دانش فعلی است که در حباب آنچه قبلا شناخته شده است راحت است.
در مثال زیر خواهیم دید که چگونه این مفاهیم در یک مسئله واقعی کاربرد دارند.
یک راهزن چند مسلح
ما اکنون به یک مثال عملی از یک مسئله یادگیری تقویتی – the راهزن چند مسلح مسئله.
راهزن چند دستی یکی از محبوب ترین مشکلات در RL است:
شما به طور مکرر با یک انتخاب از میان k گزینه یا اقدامات مختلف روبرو هستید. پس از هر انتخاب، یک پاداش عددی انتخاب شده از توزیع احتمال ثابت دریافت می کنید که بستگی دارد روی اقدامی که انتخاب کردید هدف شما این است که کل پاداش مورد انتظار را در یک دوره زمانی به حداکثر برسانید، به عنوان مثال، بیش از 1000 انتخاب اقدام یا مرحله زمانی.
شما می توانید آن را در قیاس با یک ماشین اسلات (یک راهزن یک دست) در نظر بگیرید. هر انتخاب اکشن مانند بازی یکی از اهرمهای دستگاه اسلات است و پاداشهایی که برای رسیدن به جکپات به دست میآیند.

حل این مشکل به این معنی است که ما می توانیم به یک بهینه برسیم خط مشی: استراتژی که به ما امکان می دهد در هر مرحله زمانی بهترین اقدام ممکن (آنی که بالاترین بازده مورد انتظار را دارد) انتخاب کنیم.
روشهای عمل ارزش
یک راه حل بسیار ساده است روی تابع مقدار عمل به یاد داشته باشید که یک مقدار عمل، پاداش میانگین زمانی است که آن عمل انتخاب می شود:
$$ q(a) = E(R_t \mid A=a) $$
ما به راحتی می توانیم تخمین بزنیم q با استفاده از میانگین نمونه:
$$ Q_t(a) = \frac{\text{مجموع جوایز زمانی که “a” قبل از “t” گرفته شده است}}{\text{تعداد دفعاتی که “a” قبل از “t” گرفته شده است}} $$
اگر مشاهدات کافی جمع آوری کنیم، تخمین ما به اندازه کافی به تابع واقعی نزدیک می شود. سپس می توانیم در هر مرحله حریصانه عمل کنیم، یعنی اقدامی را با بالاترین ارزش انتخاب کنیم تا بالاترین پاداش ممکن را جمع آوری کنیم.
زیاد حریص نباش
زمانی را به خاطر می آورید که از مبادله بین اکتشاف و بهره برداری صحبت کردیم؟ این یک نمونه از این است که چرا باید به آن اهمیت دهیم.
در واقع، اگر همانطور که در پاراگراف قبل پیشنهاد شد، همیشه حریصانه عمل کنیم، هرگز اقدامات غیربهینه را امتحان نمی کنیم که در نهایت ممکن است به نتایج بهتری منجر شود.
برای معرفی درجه ای از کاوش در راه حل خود، می توانیم از یک استفاده کنیم ε-طمع استراتژی: ما در بیشتر مواقع اقداماتی را با حرص انتخاب می کنیم، اما هر چند وقت یکبار، با احتمال ε، یک عمل تصادفی را بدون توجه به مقادیر عمل انتخاب می کنیم.
به نظر می رسد که این روش اکتشاف ساده بسیار خوب عمل می کند و می تواند پاداش های دریافتی ما را به میزان قابل توجهی افزایش دهد.
یک نکته آخر – برای جلوگیری از گران شدن راه حل ما از نظر محاسباتی، میانگین را به صورت تدریجی طبق این فرمول محاسبه می کنیم:
$$ Q_{n+1} = Q_n + \frac{1}{n}(R_n – Q_n) $$
راه حل پایتون
import numpy as np
k = 3
Q = (0 for _ in range(k))
N = (0 for _ in range(k))
eps = 0.1
p_bandits = (0.45, 0.40, 0.80)
def pull(a):
"""Pull arm of bandit with index `i` and return 1 if win,
else return 0."""
if np.random.rand() < p_bandits(a):
return 1
else:
return 0
while True:
if np.random.rand() > eps:
a = np.argmax(Q)
else:
a = np.random.randint(0, k)
reward = pull(a)
N(a) += 1
Q(a) += 1/N(a) * (reward - Q(a))
و voilà! اگر این اسکریپت را برای چند ثانیه اجرا کنیم، از قبل می بینیم که مقادیر عمل ما با احتمال ضربه زدن به جکپات برای راهزنان ما متناسب است:
0.4406301434281669,
0.39131455399060977,
0.8008844354479673
این بدان معنی است که سیاست حریصانه ما به درستی به نفع اقداماتی است که می توانیم از آنها انتظار پاداش بیشتری داشته باشیم.
نتیجه
یادگیری تقویتی یک زمینه رو به رشد است و موارد زیادی برای پوشش دادن وجود دارد. در واقع، ما هنوز به الگوریتمها و مدلهای همه منظوره (مثلاً برنامهنویسی پویا، مونت کارلو، تفاوت زمانی) نگاه نکردهایم.
در حال حاضر مهمترین چیز این است که با مفاهیمی مانند توابع ارزش، سیاست ها و MDP ها آشنا شوید. در منابع در بخش این مقاله، منابع بسیار خوبی برای به دست آوردن درک عمیق تر از این نوع مطالب پیدا خواهید کرد.
منابع
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-23 01:40:10



