از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
ایجاد یک شبکه عصبی از ابتدا در پایتون: افزودن لایه های پنهان
سرفصلهای مطلب
این دومین مقاله از سری مقالات است روی “ایجاد یک شبکه عصبی از ابتدا در پایتون”.
اگر شما کاملا مبتدی در شبکه های عصبی هستید، ابتدا باید قسمت 1 این مجموعه را بخوانید (پیوند بالا). هنگامی که با مفاهیم توضیح داده شده در آن مقاله راحت شدید، می توانید برگردید و با این مقاله ادامه دهید.
معرفی
در مقاله قبلی بحث خود را در مورد شبکه های عصبی مصنوعی آغاز کردیم. ما دیدیم که چگونه یک شبکه عصبی ساده با یک لایه ورودی و یک خروجی، از ابتدا در پایتون ایجاد کنیم. چنین شبکه عصبی پرسپترون نامیده می شود. با این حال، شبکه های عصبی دنیای واقعی، که قادر به انجام وظایف پیچیده مانند طبقه بندی تصاویر و تحلیل بازار سهام هستند، علاوه بر لایه ورودی و خروجی، حاوی چندین لایه پنهان هستند.
در مقاله قبلی، به این نتیجه رسیدیم که یک Perceptron قادر به یافتن مرز تصمیم خطی است. ما از پرسپترون برای پیش بینی اینکه آیا یک فرد دیابتی است یا نه از مجموعه داده اسباب بازی استفاده کردیم. با این حال، یک پرسپترون قادر به یافتن مرزهای تصمیم غیرخطی نیست.
در این مقاله، ما بر اساس مفاهیمی که در قسمت 1 این مجموعه مطالعه کردیم، استفاده خواهیم کرد و یک شبکه عصبی با یک لایه ورودی، یک لایه پنهان و یک لایه خروجی ایجاد خواهیم کرد. خواهیم دید که شبکه عصبی که توسعه خواهیم داد قادر به یافتن مرزهای غیرخطی خواهد بود.
مجموعه داده
برای این مقاله به داده های غیرخطی قابل تفکیک نیاز داریم. به عبارت دیگر، ما به مجموعه داده ای نیاز داریم که با استفاده از خط مستقیم قابل طبقه بندی نباشد.
خوشبختانه پایتون Scikit Learn کتابخانه با ابزارهای مختلفی ارائه می شود که می توان از آنها برای تولید خودکار انواع مختلف مجموعه داده استفاده کرد.
اسکریپت زیر را برای تولید مجموعه داده ای که قرار است از آن استفاده کنیم، به منظور آموزش و آزمایش شبکه عصبی خود اجرا کنید.
from sklearn import datasets
np.random.seed(0)
feature_set, labels = datasets.make_moons(100, noise=0.10)
plt.figure(figsize=(10,7))
plt.scatter(feature_set(:,0), feature_set(:,1), c=labels, cmap=plt.cm.winter)
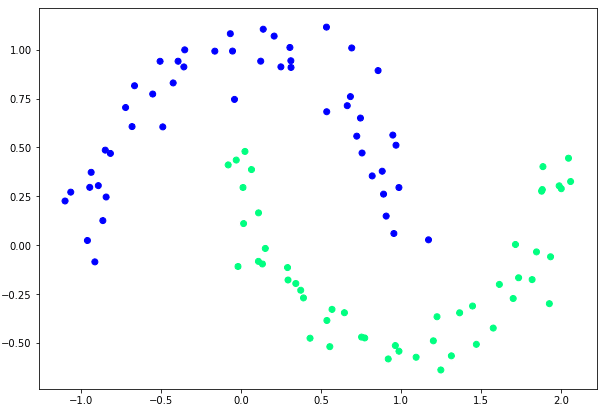
در اسکریپت بالا ما import را datasets کلاس از sklearn کتابخانه برای ایجاد مجموعه داده غیر خطی از 100 نقطه داده، از make_moons متد و آن را به عنوان پارامتر اول 100 ارسال کنید. این متد یک مجموعه داده را برمی گرداند که وقتی رسم می شود شامل دو نیم دایره متقابل است، همانطور که در شکل زیر نشان داده شده است:

شما به وضوح می بینید که این داده ها را نمی توان با یک خط مستقیم جدا کرد، بنابراین از پرسپترون نمی توان برای طبقه بندی صحیح این داده ها استفاده کرد.
بیایید این مفهوم را تأیید کنیم. برای انجام این کار، از یک پرسپترون ساده با یک لایه ورودی و یک لایه خروجی (لایهای که در مقاله گذشته ایجاد کردیم) استفاده میکنیم و سعی میکنیم مجموعه داده «قمر» خود را طبقهبندی کنیم. اسکریپت زیر را اجرا کنید:
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
feature_set, labels = datasets.make_moons(100, noise=0.10)
plt.figure(figsize=(10,7))
plt.scatter(feature_set(:,0), feature_set(:,1), c=labels, cmap=plt.cm.winter)
labels = labels.reshape(100, 1)
def sigmoid(x):
return 1/(1+np.exp(-x))
def sigmoid_der(x):
return sigmoid(x) *(1-sigmoid (x))
np.random.seed(42)
weights = np.random.rand(2, 1)
lr = 0.5
bias = np.random.rand(1)
for epoch in range(200000):
inputs = feature_set
XW = np.dot(feature_set,weights) + bias
z = sigmoid(XW)
error_out = ((1 / 2) * (np.power((z - labels), 2)))
print(error_out.sum())
error = z - labels
dcost_dpred = error
dpred_dz = sigmoid_der(z)
z_delta = dcost_dpred * dpred_dz
inputs = feature_set.T
weights -= lr * np.dot(inputs, z_delta)
for num in z_delta:
bias -= lr * num
خواهید دید که مقدار میانگین مربعات خطا، مهم نیست که چه کاری انجام دهید، بیش از 4.17 درصد همگرا نخواهد شد. این به ما نشان می دهد که نمی توانیم با استفاده از این پرسپترون همه نقاط مجموعه داده را به درستی طبقه بندی کنیم، مهم نیست که چه کاری انجام می دهیم.
شبکه های عصبی با یک لایه پنهان
در این قسمت یک شبکه عصبی با یک لایه ورودی، یک لایه پنهان و یک لایه خروجی ایجاد می کنیم. معماری شبکه عصبی ما به صورت زیر خواهد بود:

در شکل بالا یک شبکه عصبی با 2 ورودی، یک لایه پنهان و یک لایه خروجی داریم. لایه پنهان دارای 4 گره است. لایه خروجی 1 دارد node از آنجایی که ما در حال حل یک مسئله طبقه بندی باینری هستیم، که در آن تنها دو خروجی ممکن می تواند وجود داشته باشد. این معماری شبکه عصبی قادر به یافتن مرزهای غیر خطی است.
مهم نیست که چند گره و لایه پنهان در شبکه عصبی وجود دارد، اصل کار یکسان باقی می ماند. شما با فاز پیشخور شروع میکنید که در آن ورودیهای لایه قبلی با وزنهای مربوطه ضرب میشوند و از تابع فعالسازی عبور میکنند تا مقدار نهایی مربوط به آن به دست آید. node در لایه بعدی این process برای تمام لایه های پنهان تکرار می شود تا خروجی محاسبه شود. در مرحله پس انتشار، خروجی پیش بینی شده با خروجی واقعی مقایسه شده و هزینه خطا محاسبه می شود. هدف به حداقل رساندن تابع هزینه است.
همانطور که در مقاله قبلی دیدیم، اگر هیچ لایه پنهانی وجود نداشته باشد، بسیار ساده است.
با این حال، اگر یک یا چند لایه پنهان درگیر باشد، process کمی پیچیده تر می شود زیرا خطا باید به بیش از یک لایه بازگردانده شود زیرا وزن ها در همه لایه ها به خروجی نهایی کمک می کنند.
در این مقاله روش انجام مراحل feed-forward و back-propagation برای شبکه عصبی دارای یک یا چند لایه پنهان را خواهیم دید.
فید فوروارد
برای هر رکورد، دو ویژگی “x1” و “x2” داریم. برای محاسبه مقادیر برای هر کدام node در لایه پنهان، باید ورودی را با وزن های مربوطه ضرب کنیم node که برای آن مقدار را محاسبه می کنیم. سپس محصول نقطهای را از یک تابع فعالسازی عبور میدهیم تا مقدار نهایی را بدست آوریم.
به عنوان مثال برای محاسبه مقدار نهایی برای اولین node در لایه پنهان که با “ah1” مشخص می شود، باید محاسبه زیر را انجام دهید:
$$
zh1 = x1w1 + x2w2
$$
$$
ah1 = \frac{\mathrm{1} }{\mathrm{1} + e^{-zh1} }
$$
این مقدار به دست آمده برای بالاترین بیشترین است node در لایه پنهان به همین ترتیب، می توانید مقادیر گره های 2، 3 و 4 لایه پنهان را محاسبه کنید.
به طور مشابه، برای محاسبه مقدار لایه خروجی، مقادیر موجود در گره های لایه پنهان به عنوان ورودی در نظر گرفته می شوند. بنابراین، برای محاسبه خروجی، مقادیر گره های لایه پنهان را با وزن مربوط به آنها ضرب کنید و نتیجه را از طریق یک تابع فعال سازی عبور دهید.
این عملیات را می توان به صورت ریاضی با معادله زیر بیان کرد:
$$
zo = ah1w9 + ah2w10 + ah3w11 + ah4w12
$$
$$
a0 = \frac{\mathrm{1} }{\mathrm{1} + e^{-z0} }
$$
در اینجا “a0” خروجی نهایی شبکه عصبی ما است. به یاد داشته باشید که تابع فعال سازی که ما استفاده می کنیم تابع sigmoid است، همانطور که در مقاله قبلی انجام دادیم.
توجه داشته باشید: به منظور سادگی، ما یک اصطلاح تعصب به هر وزن اضافه نکردیم. خواهید دید که شبکه عصبی با لایه پنهان حتی بدون عبارت بایاس بهتر از پرسپترون عمل خواهد کرد.
انتشار پشت
گام پیشروی نسبتاً مستقیم است. با این حال، انتشار به عقب مانند قسمت 1 این مجموعه ساده نیست.
در مرحله پس انتشار، ابتدا تابع ضرر خود را تعریف می کنیم. ما استفاده خواهیم کرد خطای میانگین مربعات تابع هزینه. می توان آن را به صورت ریاضی به صورت زیر نشان داد:
$$
MSE =
\frac{\mathrm{1} }{\mathrm{n}}
\sum\nlimits_{i=1}^{n}
(پیش بینی شده – مشاهده شده)^{2}
$$
اینجا n تعداد مشاهدات است.
فاز 1
در مرحله اول انتشار مجدد، باید وزن لایه خروجی یعنی w9، w10، w11 و w12 را به روز کنیم. بنابراین در حال حاضر، فقط در نظر بگیرید که شبکه عصبی ما دارای بخش زیر است:

این به نظر شبیه پرسپترونی است که در مقاله گذشته توسعه دادیم. هدف از مرحله اول انتشار برگشتی، به روز رسانی وزن های w9، w10، w11 و w12 به گونه ای است که خطای نهایی به حداقل برسد. این یک مشکل بهینه سازی جایی که باید پیدا کنیم حداقل عملکرد برای تابع هزینه ما
برای یافتن مینیمم یک تابع، می توانیم از عبارت استفاده کنیم شیب مناسب الگوریتم الگوریتم نزول گرادیان را می توان به صورت ریاضی به صورت زیر نشان داد:
$$ تکرار \ تا \ همگرایی: \begin{Bmatrix} w_j := w_j – \alpha \frac{\partial }{\partial w_j} J(w_0,w_1 ……. w_n) \end{Bmatrix} …………. (1) $$
جزئیات در مورد اینکه چگونه تابع نزولی گرادیان هزینه را به حداقل می رساند قبلاً در مقاله قبلی مورد بحث قرار گرفته است. در اینجا ما فقط عملیات ریاضی را می بینیم که باید انجام دهیم.
تابع هزینه ما این است:
$$
MSE = \frac{\mathrm{1} }{\mathrm{n}} \sum\nolimits_{i=1}^{n}(پیشبینی شده – مشاهده شده)^{2}
$$
در شبکه عصبی ما، خروجی پیش بینی شده با “ao” نشان داده می شود. به این معنی که اساسا باید این تابع را کمینه کنیم:
$$
هزینه = \frac{\mathrm{1} }{\mathrm{n}} \sum\nolimits_{i=1}^{n}(ao – مشاهده شده)^{2}
$$
از مقاله قبل، می دانیم که برای به حداقل رساندن تابع هزینه، باید مقادیر وزن را طوری به روز کنیم که هزینه کاهش یابد. برای انجام این کار، باید از تابع هزینه با توجه به هر وزن مشتق بگیریم. از آنجایی که در این مرحله با وزن های لایه خروجی سروکار داریم، باید تابع هزینه را با توجه به w9، w10، w11 و w2 متمایز کنیم.
تمایز تابع هزینه با توجه به وزن ها در لایه خروجی را می توان به صورت ریاضی به صورت زیر با استفاده از قاعده زنجیره ای از تمایز
$$
\frac {dcost}{dwo} = \frac {dcost}{dao} *, \frac {dao}{dzo} * \frac {dzo}{dwo} …… (1)
$$
در اینجا “wo” به وزن های موجود در لایه خروجی اشاره دارد. حرف “د” در ابتدای هر عبارت به “مشتق” اشاره دارد.
بیایید مقدار هر عبارت را در آن پیدا کنیم معادله 1.
اینجا،
$$
\frac {dcost}{dao} = \frac {2}{n} * (ao – labels)
$$
اینجا 2 و n ثابت هستند. اگر آنها را نادیده بگیریم، معادله زیر را داریم.
$$
\frac {dcost}{dao} = (ao – labels) …….. (5)
$$
در مرحله بعد، می توانیم “dao” را با توجه به “dzo” به صورت زیر پیدا کنیم:
$$
\frac {dao}{dzo} = sigmoid(zo) * (1-sigmoid(zo)) …….. (6)
$$
در نهایت، ما باید “dzo” را با توجه به “dwo” پیدا کنیم. مشتق به سادگی ورودی هایی است که از لایه مخفی همانطور که در زیر نشان داده شده است:
$$
\frac {dzo}{dwo} = آه
$$
در اینجا “ah” به 4 ورودی از لایه های پنهان اشاره دارد. معادله 1 می توان برای یافتن مقادیر وزن به روز شده برای وزن های لایه خروجی استفاده کرد. برای یافتن مقادیر وزن جدید، مقادیر توسط معادله 1 را می توان به سادگی با نرخ یادگیری ضرب کرد و از مقادیر وزن فعلی کم کرد. این ساده است و ما قبلاً این کار را انجام داده ایم.
فاز 2
در قسمت قبل دیدیم که چگونه میتوانیم مقادیر بهروز شده برای وزنهای لایه خروجی یعنی w9، w10، w11 و 12 را پیدا کنیم. در این بخش، خطای خود را به لایه قبلی باز میگردانیم و مقادیر وزن جدید را پیدا میکنیم. برای وزن های لایه پنهان یعنی وزن های w1 تا w8.
بیایید مجموعاً وزن لایه های پنهان را به عنوان “wh” نشان دهیم. ما اساساً باید تابع هزینه را با توجه به “wh” متمایز کنیم. از نظر ریاضی می توانیم از قانون زنجیره تمایز برای نمایش آن به صورت زیر استفاده کنیم:
$$
\frac {dcost}{dwh} = \frac {dcost}{dah} *, \frac {dah}{dzh} * \frac {dzh}{dwh} …… (2)
$$
اینجا دوباره شکست خواهیم خورد معادله 2 به شرایط فردی
اولین عبارت “dcost” را می توان با توجه به “dah” با استفاده از قانون زنجیره ای تمایز به صورت زیر متمایز کرد:
$$
\frac {dcost}{dah} = \frac {dcost}{dzo} *, \frac {dzo}{dah} …… (3)
$$
بیایید دوباره آن را بشکنیم معادله 3 به شرایط فردی با استفاده از قانون زنجیره ای دوباره، می توانیم “dcost” را با توجه به “dzo” به صورت زیر متمایز کنیم:
$$
\frac {dcost}{dzo} = \frac {dcost}{dao} *، \frac {dao}{dzo} …… (4)
$$
ما قبلاً مقدار dcost/dao in را محاسبه کردهایم معادله 5 و dao/dzo در _معادله 6 _.
حالا باید dzo/dah را پیدا کنیم معادله 3. اگر به zo نگاه کنیم مقدار زیر را دارد:
$$
zo = a01w9 + a02w10 + a03w11 + a04w12
$$
اگر آن را با توجه به تمام ورودی ها از لایه پنهان که با “ao” نشان داده شده است، متمایز کنیم، در این صورت تمام وزن های لایه خروجی که با “wo” نشان داده شده اند باقی می مانند. از این رو،
$$
\frac {dzo}{dah} = wo …… (7)
$$
اکنون می توانیم مقدار dcost/dah را با جایگزین کردن مقادیر از پیدا کنیم معادلات 7 و 4 که در معادله 3.
برگشتن به معادله 2، ما هنوز dah/dzh و dzh/dwh را پیدا نکرده ایم.
اولین ترم dah/dzh را می توان به صورت زیر محاسبه کرد:
$$
\frac {dah}{dzh} = sigmoid(zh) * (1-sigmoid(zh)) …….. (8)
$$
و در نهایت، dzh/dwh به سادگی مقادیر ورودی است:
$$
\frac {dzh}{dwh} = ویژگی های ورودی …….. (9)
$$
اگر مقادیر از را جایگزین کنیم معادلات 3، 8 و 9 که در معادله 3، می توانیم ماتریس به روز شده برای وزن لایه های پنهان را دریافت کنیم. برای یافتن مقادیر وزن جدید برای وزنهای لایه پنهان “wh”، مقادیر برگردانده شده توسط معادله 2 را می توان به سادگی با نرخ یادگیری ضرب کرد و از مقادیر وزن فعلی کم کرد. و تقریباً همین است.
معادلات ممکن است برای شما خسته کننده به نظر برسند زیرا محاسبات زیادی در حال انجام است. با این حال، اگر از نزدیک به آنها نگاه کنید، فقط دو عملیات در یک زنجیره انجام می شود: مشتق و ضرب.
یکی از دلایل کندتر بودن شبکههای عصبی نسبت به سایر الگوریتمهای یادگیری ماشینی، این واقعیت است که محاسبات زیادی در انتهای پشتی انجام میشود. شبکه عصبی ما فقط یک لایه پنهان با چهار گره، دو ورودی و یک خروجی داشت، با این حال ما مجبور بودیم عملیات استخراج و ضرب طولانی را انجام دهیم تا وزن ها را برای یک تکرار به روز کنیم. در دنیای واقعی، شبکه های عصبی می توانند صدها لایه با صدها مقدار ورودی و خروجی داشته باشند. بنابراین، شبکه های عصبی به کندی اجرا می شوند.
کد شبکه های عصبی با یک لایه پنهان
حالا بیایید شبکه عصبی را که در پایتون در مورد آن صحبت کردیم از ابتدا پیاده سازی کنیم. شما به وضوح مطابقت بین قطعات کد و نظریه ای را که در بخش قبل مورد بحث قرار دادیم مشاهده خواهید کرد. ما دوباره سعی می کنیم داده های غیر خطی را که در بخش Dataset مقاله ایجاد کرده ایم طبقه بندی کنیم. به اسکریپت زیر دقت کنید.
# -*- coding: utf-8 -*-
"""
Created روی Tue Sep 25 13:46:08 2018
@author: usman
"""
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
feature_set, labels = datasets.make_moons(100, noise=0.10)
plt.figure(figsize=(10,7))
plt.scatter(feature_set(:,0), feature_set(:,1), c=labels, cmap=plt.cm.winter)
labels = labels.reshape(100, 1)
def sigmoid(x):
return 1/(1+np.exp(-x))
def sigmoid_der(x):
return sigmoid(x) *(1-sigmoid (x))
wh = np.random.rand(len(feature_set(0)),4)
wo = np.random.rand(4, 1)
lr = 0.5
for epoch in range(200000):
# feedforward
zh = np.dot(feature_set, wh)
ah = sigmoid(zh)
zo = np.dot(ah, wo)
ao = sigmoid(zo)
# Phase1 =======================
error_out = ((1 / 2) * (np.power((ao - labels), 2)))
print(error_out.sum())
dcost_dao = ao - labels
dao_dzo = sigmoid_der(zo)
dzo_dwo = ah
dcost_wo = np.dot(dzo_dwo.T, dcost_dao * dao_dzo)
# Phase 2 =======================
# dcost_w1 = dcost_dah * dah_dzh * dzh_dw1
# dcost_dah = dcost_dzo * dzo_dah
dcost_dzo = dcost_dao * dao_dzo
dzo_dah = wo
dcost_dah = np.dot(dcost_dzo , dzo_dah.T)
dah_dzh = sigmoid_der(zh)
dzh_dwh = feature_set
dcost_wh = np.dot(dzh_dwh.T, dah_dzh * dcost_dah)
# Update Weights ================
wh -= lr * dcost_wh
wo -= lr * dcost_wo
در اسکریپت بالا با وارد کردن کتابخانه های مورد نظر شروع می کنیم و سپس مجموعه داده خود را ایجاد می کنیم. سپس تابع سیگموئید را به همراه مشتق آن تعریف می کنیم. سپس وزن لایه پنهان و لایه خروجی را با مقادیر تصادفی مقداردهی اولیه می کنیم. میزان یادگیری 0.5 است. من نرخ های مختلف یادگیری را امتحان کردم و متوجه شدم که 0.5 مقدار خوبی است.
سپس الگوریتم را برای 2000 دوره اجرا می کنیم. در داخل هر دوره، ابتدا عملیات فید فوروارد را انجام می دهیم. قطعه کد برای عملیات فید فوروارد به شرح زیر است:
zh = np.dot(feature_set, wh)
ah = sigmoid(zh)
zo = np.dot(ah, wo)
ao = sigmoid(zo)
همانطور که در بخش تئوری بحث شد، انتشار برگشتی شامل دو مرحله است. در مرحله اول، گرادیان برای وزن لایه خروجی محاسبه می شود. اسکریپت زیر در مرحله اول انتشار مجدد اجرا می شود.
error_out = ((1 / 2) * (np.power((ao - labels), 2)))
print(error_out.sum())
dcost_dao = ao - labels
dao_dzo = sigmoid_der(zo)
dzo_dwo = ah
dcost_wo = np.dot(dzo_dwo.T, dcost_dao * dao_dzo)
در مرحله دوم، گرادیان برای وزن لایه پنهان محاسبه می شود. اسکریپت زیر در مرحله دوم انتشار مجدد اجرا می شود.
dcost_dzo = dcost_dao * dao_dzo
dzo_dah = wo
dcost_dah = np.dot(dcost_dzo , dzo_dah.T)
dah_dzh = sigmoid_der(zh)
dzh_dwh = feature_set
dcost_wh = np.dot( dzh_dwh.T, dah_dzh * dcost_dah)
در نهایت، وزن ها در اسکریپت زیر به روز می شوند:
wh -= lr * dcost_wh
wo -= lr * dcost_wo
هنگامی که اسکریپت بالا اجرا می شود، حداقل مقدار خطای میانگین مربع 1.50 را خواهید دید که کمتر از میانگین مربع خطای قبلی ما 4.17 است که با استفاده از پرسپترون به دست آمده بود. این نشان می دهد که شبکه عصبی با لایه های پنهان در مورد داده های غیرخطی قابل جداسازی بهتر عمل می کند.
نتیجه
در این مقاله دیدیم که چگونه می توانیم یک شبکه عصبی با 1 لایه پنهان، از ابتدا در پایتون ایجاد کنیم. ما دیدیم که چگونه شبکه عصبی ما از یک شبکه عصبی بدون لایههای پنهان برای طبقهبندی باینری دادههای غیرخطی بهتر عمل کرد.
با این حال، ممکن است لازم باشد داده ها را به بیش از دو دسته طبقه بندی کنیم. در مقاله بعدی ما روش ایجاد یک شبکه عصبی از ابتدا در پایتون برای مشکلات طبقه بندی چند کلاسه را خواهیم دید.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-26 23:05:04



