از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
راهنمای هش جداول در پایتون
سرفصلهای مطلب
معرفی
جداول هش روشی کارآمد و منعطف برای ذخیره و بازیابی داده ها را ارائه می دهد و آنها را برای کارهایی که شامل مجموعه داده های بزرگ یا نیاز به دسترسی سریع به موارد ذخیره شده است ضروری می کند.
در حالی که پایتون ساختار داده ای داخلی ندارد که به صراحت a نامیده می شود “جدول هش”، فراهم می کند فرهنگ لغت، که شکلی از جدول هش است. دیکشنری های پایتون مجموعه های نامرتب هستند جفت های کلید-مقدار، که در آن کلید منحصر به فرد است و دارای مقدار مربوطه است. با تشکر از a process شناخته شده به عنوان “هش کردن”، دیکشنری ها بازیابی، افزودن و حذف موثر مدخل ها را امکان پذیر می کنند.
توجه داشته باشید: اگر یک برنامه نویس پایتون هستید و تا به حال از فرهنگ لغت برای ذخیره داده ها به عنوان جفت کلید-مقدار استفاده کرده اید، قبلاً از فناوری جدول هش بهره برده اید بدون اینکه لزوماً آن را بدانید! دیکشنری های پایتون با استفاده از جداول هش پیاده سازی می شوند!
در این راهنما، ما به دنیای جداول هش می پردازیم. ما با اصول اولیه شروع می کنیم و توضیح می دهیم که جداول هش چیست و چگونه کار می کنند. ما همچنین پیادهسازی جداول هش پایتون را از طریق فرهنگ لغت بررسی میکنیم، راهنمای گام به گام ایجاد جدول هش در پایتون و حتی لمس را ارائه میکنیم. روی چگونه برخوردهای هش را مدیریت کنیم در طول مسیر، ما کاربرد و کارایی جداول هش را با مثالهای واقعی و تکههای مفید پایتون نشان خواهیم داد.
تعریف جداول هش: ساختار داده جفت کلید-مقدار
از آنجایی که دیکشنری ها در پایتون اساسا پیاده سازی جداول هش هستند، اجازه دهید ابتدا تمرکز کنیم روی جداول هش در واقع چه هستند و سپس وارد پیاده سازی پایتون شوید.
جداول هش نوعی ساختار داده است که مکانیزمی برای ذخیره داده ها در یک فراهم می کند شیوه انجمنی. در یک جدول هش، داده ها در یک ذخیره می شوند فرمت آرایه، اما هر مقدار داده خاص خود را دارد کلید منحصر به فرد، که برای شناسایی داده ها استفاده می شود. این مکانیسم مبتنی است روی جفت های کلید-مقدار، که بازیابی داده ها را سریع می کند process.
تشبیهی که اغلب برای توضیح این مفهوم استفاده می شود، فرهنگ لغت دنیای واقعی است. در یک فرهنگ لغت، شما از یک کلمه شناخته شده (“کلید”) برای پیدا کردن معنای آن (“ارزش”) استفاده می کنید. اگر کلمه را بلد باشید، می توانید به سرعت تعریف آن را پیدا کنید. به طور مشابه، در جدول هش، اگر کلید را بدانید، می توانید به سرعت مقدار آن را بازیابی کنید.
اساساً، ما سعی میکنیم جفتهای کلید-مقدار را به کارآمدترین شکل ممکن ذخیره کنیم.
به عنوان مثال، فرض کنید می خواهیم یک جدول هش ایجاد کنیم که ماه تولد افراد مختلف را ذخیره کند. نام مردم کلید ماست و ماه تولد آنها ارزش هاست:
+-----------------------+
| Key | Value |
+-----------------------+
| Alice | January |
| Bob | May |
| Charlie | January |
| David | August |
| Eve | December |
| Brian | May |
+-----------------------+
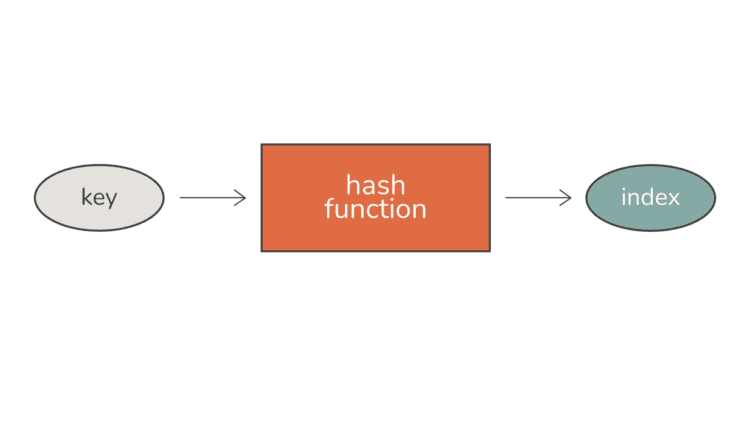
برای ذخیره این جفتهای کلید-مقدار در یک جدول هش، ابتدا به راهی برای تبدیل مقدار کلیدها به شاخصهای مناسب آرایهای نیاز داریم که یک جدول هش را نشان میدهد. آنجاست که یک تابع هش وارد بازی می شود! این تابع که ستون فقرات اجرای جدول هش است، کلید را پردازش می کند و شاخص مربوطه را در آرایه ذخیره سازی داده برمی گرداند – درست همانطور که ما نیاز داریم.
هدف الف عملکرد هش خوب توزیع یکنواخت کلیدها در سراسر آرایه، به حداقل رساندن احتمال برخورد (که در آن دو کلید یک شاخص تولید می کنند) است.

در واقعیت، توابع هش بسیار پیچیدهتر هستند، اما برای سادگی، از یک تابع درهمسازی استفاده میکنیم که با گرفتن مقدار ASCII حرف اول مدول نام به اندازه جدول، هر نام را به یک شاخص نگاشت میکند:
def simple_hash(key, array_size):
return ord(key(0)) % array_size
این تابع هش است ساده، اما آن می تواند منجر به برخورد شود زیرا ممکن است کلیدهای مختلف با یک حرف شروع شوند و از این رو شاخص های حاصل یکسان خواهند بود. به عنوان مثال، بگوییم آرایه ما به اندازه است 10، در حال اجرا simple_hash(key, 10) برای هر یک از کلیدهای ما به ما می دهد:

از طرف دیگر، میتوانیم این دادهها را به روشی مختصرتر تغییر شکل دهیم:
+---------------------+
| Key | Index |
+---------------------+
| Alice | 5 |
| Bob | 6 |
| Charlie | 7 |
| David | 8 |
| Eve | 9 |
| Brian | 6 |
+---------------------+
اینجا، Bob و Brian در آرایه به دست آمده اندیس یکسانی داشته باشند که نتیجه آن است یک برخورد. در بخشهای آخر بیشتر در مورد برخوردها صحبت خواهیم کرد – هم از نظر ایجاد توابع هش که احتمال برخورد را به حداقل میرساند و هم از نظر رفع تصادم هنگام وقوع.
طراحی توابع هش قوی یکی از مهمترین جنبه های کارایی جدول هش است!
توجه داشته باشید: در پایتون، دیکشنری ها پیاده سازی یک جدول هش هستند، که در آن کلیدها هش می شوند و مقدار هش به دست آمده تعیین می کند که مقدار مربوطه در کجای ذخیره سازی داده های زیرین فرهنگ لغت قرار می گیرد.
در بخشهای بعدی، عمیقتر به عملکرد داخلی جداول هش میپردازیم، در مورد عملکرد آنها، مسائل احتمالی (مانند برخوردها) و راهحلهای این مشکلات بحث میکنیم.
ابهام زدایی از نقش توابع هش در جداول هش
توابع هش هستند قلب و روح از جداول هش آنها به عنوان پلی بین کلیدها و مقادیر مرتبط با آنها عمل می کنند و وسیله ای برای ذخیره سازی و بازیابی موثر داده ها فراهم می کنند. درک نقش توابع هش در جداول هش برای درک روش عملکرد این ساختار داده قدرتمند بسیار مهم است.
تابع هش چیست؟
در زمینه جداول هش، یک تابع هش تابع خاصی است که a را می گیرد کلید به عنوان ورودی و یک شاخص برمی گرداند که مقدار مربوطه باید ذخیره یا از آن بازیابی شود. این کلید را به یک تبدیل می کند هش – عددی که مربوط به شاخصی در آرایه است که ساختار زیربنایی جدول هش را تشکیل می دهد.
تابع هش باید باشد قطعی، به این معنی که همیشه باید همان هش را برای یک کلید تولید کند. به این ترتیب، هر زمان که بخواهید مقداری را بازیابی کنید، می توانید از تابع هش استفاده کنید روی کلید برای پیدا کردن محل ذخیره مقدار.
نقش توابع هش در جداول هش
هدف اصلی یک تابع هش در جدول هش، توزیع کلیدها است تا حد امکان یکنواخت در سراسر آرایه این مهم است زیرا توزیع یکنواخت کلیدها امکان پیچیدگی زمانی ثابت را فراهم می کند O (1) برای عملیات داده مانند درج، حذف، و بازیابی روی میانگین.
برای نشان دادن روش عملکرد یک تابع هش در جدول هش، اجازه دهید دوباره به مثال قسمت قبل نگاهی بیندازیم:
+-----------------------+
| Key | Value |
+-----------------------+
| Alice | January |
| Bob | May |
| Charlie | January |
| David | August |
| Eve | December |
| Brian | May |
+-----------------------+
مانند قبل، فرض کنید یک تابع هش داریم، simple_hash(key)و یک جدول هش اندازه 10.
همانطور که قبلاً دیده ایم، دویدن، بگویید، "Alice" از طریق simple_hash() تابع ایندکس را برمی گرداند 5. یعنی می توانیم عنصر را با کلید پیدا کنیم "Alice" و ارزش "January" در آرایه ای که جدول هش را نشان می دهد، روی شاخص 5 (عنصر ششم آن آرایه):

و این برای هر کلید از داده های اصلی ما صدق می کند. اجرای هر کلید از طریق تابع هش مقدار صحیح را به ما می دهد – یک شاخص در آرایه جدول هش جایی که آن عنصر ذخیره می شود:
+---------------------+
| Key | Index |
+---------------------+
| Alice | 5 |
| Bob | 6 |
| Charlie | 7 |
| David | 8 |
| Eve | 9 |
| Brian | 6 |
+---------------------+
این می تواند به راحتی به آرایه ای که یک جدول هش را نشان می دهد – یک عنصر با کلید ترجمه شود "Alice" در فهرست ذخیره می شود 5، "Bob" زیر شاخص 6، و غیره روی:

توجه داشته باشید: زیر شاخص 6 دو عنصر وجود دارد – {"Bob", "February"} و {"Brian", "May"}. در تصویر بالا، این برخورد با استفاده از روشی که نامیده می شود حل شد زنجیربندی جداگانه، که در ادامه این مقاله بیشتر در مورد آن صحبت خواهیم کرد.
زمانی که می خواهیم مقدار مربوط به کلید را بازیابی کنیم "Alice"، دوباره کلید را به تابع هش می دهیم که ایندکس را برمی گرداند 5. سپس بلافاصله به مقدار در index دسترسی پیدا می کنیم 3 از جدول هش، که است "January".
چالش ها با توابع هش
در حالی که ایده پشت توابع هش نسبتاً ساده است، طراحی یک تابع هش خوب می تواند چالش برانگیز باشد. یک نگرانی اصلی چیزی است که به عنوان a برخورد، که زمانی اتفاق می افتد که دو کلید مختلف به یک شاخص در آرایه هش می کنند.
فقط نگاهی به
"Bob"و"Brian"کلیدها در مثال ما آنها شاخص یکسانی دارند، به این معنی که در یک مکان در آرایه جدول هش ذخیره می شوند. در اصل، این نمونه ای از برخورد هشینگ است.
احتمال برخوردها توسط تابع هش و اندازه جدول هش دیکته می شود. در حالی که تقریباً غیرممکن است که به طور کامل از تصادم برای هر مقدار غیر جزئی از داده جلوگیری کرد، یک تابع هش خوب همراه با یک جدول هش با اندازه مناسب، احتمال برخورد را به حداقل می رساند.
استراتژی های مختلف مانند آدرس دهی باز و زنجیربندی جداگانه می تواند برای حل و فصل برخوردها در صورت وقوع استفاده شود که در بخش بعدی به آن خواهیم پرداخت.
تجزیه و تحلیل پیچیدگی زمانی جداول هش: مقایسه
یکی از مزایای کلیدی استفاده از جداول هش، که آنها را از بسیاری دیگر از ساختارهای داده متمایز می کند، پیچیدگی زمانی آنها برای عملیات اساسی است. پیچیدگی زمانی یک مفهوم محاسباتی است که به مدت زمانی که یک عملیات یا یک تابع برای اجرا نیاز دارد، به عنوان تابعی از اندازه ورودی برنامه اشاره دارد.
هنگام بحث از پیچیدگی زمانی، به طور کلی به سه مورد اشاره می کنیم:
- بهترین مورد: حداقل زمان لازم برای اجرای یک عملیات
- میانگین مورد: میانگین زمان مورد نیاز برای اجرای یک عملیات
- بدترین حالت: حداکثر زمان لازم برای اجرای یک عملیات
جداول هش به ویژه برای آنها قابل توجه است پیچیدگی زمانی چشمگیر در مورد متوسط سناریو. در آن سناریو، عملیات اساسی در جداول هش (درج، حذف و دسترسی به عناصر) دارای یک پیچیدگی زمانی ثابت O(1).
پیچیدگی زمانی ثابت به این معنی است که زمان صرف شده برای انجام این عملیات بدون توجه به تعداد عناصر جدول هش ثابت می ماند.
این باعث می شود که این عملیات بسیار کارآمد باشد، به خصوص زمانی که با مجموعه داده های بزرگ سروکار داریم.
در حالی که میانگین پیچیدگی زمانی مورد برای جداول هش O(1) است. را بدترین حالت سناریو داستان متفاوتی است. اگر چندین کلید به یک شاخص هش شوند (وضعیتی که به عنوان a برخورد، پیچیدگی زمانی می تواند کاهش یابد بر)، جایی که n تعداد کلیدهای نگاشت شده به یک شاخص است.
این سناریو به این دلیل اتفاق میافتد که هنگام حل تصادم، مراحل اضافی برای ذخیره و بازیابی دادهها باید انجام شود، معمولاً با عبور از فهرست پیوندی از ورودیهایی که در همان فهرست هش میشوند.
توجه داشته باشید: با یک تابع هش خوب طراحی شده و یک جدول هش با اندازه صحیح، این بدترین سناریو به طور کلی استثنا است تا معمول. یک تابع هش خوب همراه با استراتژی های حل برخورد مناسب می تواند برخوردها را به حداقل برساند.
مقایسه با سایر ساختارهای داده
در مقایسه با سایر ساختارهای داده، جداول هش به دلیل کارایی خود برجسته هستند. به عنوان مثال، عملیاتی مانند جستجو، درج و حذف در درخت جستجوی باینری متعادل یا درخت AVL متعادل دارای پیچیدگی زمانی هستند. O (log n)، که اگرچه بد نیست اما به اندازه آن کارآمد نیست O (1) پیچیدگی زمانی که جداول هش در حالت متوسط ارائه می دهد.
در حالی که آرایه ها و لیست های پیوندی ارائه می دهند O (1) پیچیدگی زمانی برای برخی از عملیات، آنها نمی توانند این سطح از کارایی را در تمام عملیات های اساسی حفظ کنند. به عنوان مثال، جستجو در یک آرایه مرتب نشده یا لیست پیوندی طول می کشد بر) زمان، و درج در یک آرایه طول می کشد بر) زمان در بدترین حالت
رویکرد پایتون به جداول هش: مقدمه ای بر دیکشنری ها
پایتون یک ساختار داده داخلی را ارائه می دهد که عملکرد یک جدول هش به نام دیکشنری را پیاده سازی می کند که اغلب به عنوان “دیکت” نامیده می شود. دیکشنری ها یکی از قدرتمندترین ساختارهای داده پایتون هستند و درک روش عملکرد آنها می تواند مهارت های برنامه نویسی شما را به میزان قابل توجهی افزایش دهد.
دیکشنری ها چیست؟
در پایتون، دیکشنری ها (dicts) مجموعه هایی نامرتب از جفت های کلید-مقدار هستند. کلیدهای یک فرهنگ لغت منحصر به فرد و غیرقابل تغییر هستند، به این معنی که پس از تنظیم نمی توان آنها را تغییر داد. این ویژگی برای عملکرد صحیح جدول هش ضروری است. ارزش های، روی از طرف دیگر، می توانند از هر نوع باشند و قابل تغییر هستند، به این معنی که شما می توانید آنها را تغییر دهید.
جفت کلید-مقدار در فرهنگ لغت به عنوان آیتم نیز شناخته می شود. هر کلید در یک فرهنگ لغت به یک مقدار مرتبط (یا نگاشت) می شود و یک جفت کلید-مقدار را تشکیل می دهد:
my_dict = {"Alice": "January", "Bob": "May", "Charlie": "January"}
دیکشنری ها در پایتون چگونه کار می کنند؟
پشت صحنه، دیکشنری های پایتون به عنوان یک جدول هش عمل می کنند. هنگامی که یک فرهنگ لغت ایجاد می کنید و یک جفت کلید-مقدار اضافه می کنید، پایتون یک تابع هش را به کلید اعمال می کند که منجر به یک مقدار هش می شود. سپس این مقدار هش تعیین می کند که مقدار مربوطه در کجا در حافظه ذخیره شود.
زیبایی این است که وقتی می خواهید مقدار را بازیابی کنید، پایتون همان تابع هش را روی کلید اعمال می کند، که بدون در نظر گرفتن اندازه فرهنگ لغت، به سرعت پایتون را به جایی که مقدار ذخیره می شود هدایت می کند:
my_dict = {}
my_dict("Alice") = "January"
print(my_dict("Alice"))
عملیات کلیدی و پیچیدگی زمانی
ساختار داده دیکشنری داخلی پایتون، انجام عملیات جدول هش اولیه – مانند درج، دسترسی، و حذف را آسان می کند. این عملیات معمولاً دارای پیچیدگی زمانی متوسط O(1) هستند که باعث کارآمدی قابل توجهی می شود.
توجه داشته باشید: مانند جداول هش، بدترین حالت پیچیدگی زمانی می تواند باشد بر)، اما این به ندرت اتفاق می افتد، فقط زمانی که برخورد هش وجود داشته باشد.
درج جفت کلید-مقدار به یک فرهنگ لغت پایتون ساده است. شما به سادگی با استفاده از عملگر انتساب یک مقدار را به یک کلید اختصاص می دهید (=). اگر کلید از قبل در فرهنگ لغت وجود نداشته باشد، اضافه می شود. اگر وجود داشته باشد، مقدار فعلی آن با مقدار جدید جایگزین می شود:
my_dict = {}
my_dict("Alice") = "January"
my_dict("Bob") = "May"
print(my_dict)
دسترسی به یک مقدار در یک فرهنگ لغت پایتون به سادگی درج یک دیکشنری است. می توانید با ارجاع به کلید در پرانتز به مقدار مربوط به یک کلید خاص دسترسی پیدا کنید. اگر سعی کنید به کلیدی دسترسی پیدا کنید که در فرهنگ لغت وجود ندارد، پایتون a را بالا می برد KeyError:
print(my_dict("Alice"))
print(my_dict("Charlie"))
برای جلوگیری از این خطا می توانید از دیکشنری استفاده کنید get() متد، که به شما امکان می دهد در صورت عدم وجود کلید، یک مقدار پیش فرض را برگردانید:
print(my_dict.get("Charlie", "Unknown"))
توجه داشته باشید: به طور مشابه، setdefault() اگر کلید از قبل وجود نداشته باشد، می توان از روش برای وارد کردن ایمن یک جفت کلید-مقدار در فرهنگ لغت استفاده کرد:
my_dict.setdefault("new_key", "default_value")
تو می توانی حذف یک جفت کلید-مقدار از دیکشنری پایتون با استفاده از del کلمه کلیدی. اگر کلید در فرهنگ لغت وجود داشته باشد، همراه با مقدار آن حذف می شود. اگر کلید وجود نداشته باشد، پایتون نیز a را افزایش می دهد KeyError:
del my_dict("Bob")
print(my_dict)
del my_dict("Bob")
مانند دسترسی، اگر میخواهید هنگام تلاش برای حذف کلیدی که وجود ندارد از بروز خطا جلوگیری کنید، میتوانید از فرهنگ لغت استفاده کنید. pop() متدی که یک کلید را حذف میکند، در صورت وجود مقدار آن را برمیگرداند و اگر وجود نداشته باشد، مقدار پیشفرض را برمیگرداند:
print(my_dict.pop("Bob", "Unknown"))
به طور کلی، دیکشنری های پایتون به عنوان یک پیاده سازی سطح بالا و کاربر پسند از جدول هش عمل می کنند. استفاده از آنها آسان است، در عین حال قدرتمند و کارآمد هستند، و آنها را به ابزاری عالی برای انجام طیف گسترده ای از وظایف برنامه نویسی تبدیل می کند.
توصیه: اگر در حال تست عضویت هستید (به عنوان مثال، آیا یک مورد در یک مجموعه قرار دارد یا خیر)، یک فرهنگ لغت (یا یک مجموعه) اغلب انتخاب کارآمدتری نسبت به یک لیست یا یک مجموعه است، به خصوص برای مجموعه های بزرگتر. دلیلش این است که دیکشنریها و مجموعهها از جداول هش استفاده میکنند که به آنها اجازه میدهد برای عضویت در زمان ثابت آزمایش کنند (O (1)) بر خلاف لیست ها یا تاپل ها که زمان خطی دارند (بر)).
در بخشهای بعدی، به جنبههای عملی استفاده از دیکشنریها در پایتون، از جمله ایجاد دیکشنری (جدول هش)، انجام عملیات و مدیریت برخوردها، عمیقتر خواهیم پرداخت.
چگونه اولین جدول هش خود را در پایتون ایجاد کنیم
دیکشنری های پایتون پیاده سازی آماده ای از جداول هش را ارائه می دهند که به شما امکان می دهد جفت های کلید-مقدار را با کارایی عالی ذخیره و بازیابی کنید. با این حال، برای درک کامل جداول هش، پیاده سازی آن از ابتدا می تواند مفید باشد. در این بخش، ما شما را از طریق ایجاد یک جدول هش ساده در پایتون راهنمایی می کنیم.
ما با تعریف a شروع می کنیم HashTable کلاس جدول هش با یک لیست ( table) و ما از یک تابع هش بسیار ساده استفاده خواهیم کرد که باقیمانده مقدار ASCII اولین کاراکتر رشته کلید تقسیم بر اندازه جدول را محاسبه می کند:
class HashTable:
def __init__(self, size):
self.size = size
self.table = (None)*size
def _hash(self, key):
return ord(key(0)) % self.size
در این کلاس، ما باید __init__() روش برای مقداردهی اولیه جدول هش و الف _hash() متد، که تابع هش ساده ما است.
در حال حاضر، ما روش ها را به خود اضافه می کنیم HashTable کلاس برای افزودن جفتهای کلید-مقدار، دریافت مقادیر بر اساس کلید و حذف ورودیها:
class HashTable:
def __init__(self, size):
self.size = size
self.table = (None)*size
def _hash(self, key):
return ord(key(0)) % self.size
def set(self, key, value):
hash_index = self._hash(key)
self.table(hash_index) = (key, value)
def get(self, key):
hash_index = self._hash(key)
if self.table(hash_index) is not None:
return self.table(hash_index)(1)
raise KeyError(f'Key {key} not found')
def remove(self, key):
hash_index = self._hash(key)
if self.table(hash_index) is not None:
self.table(hash_index) = None
else:
raise KeyError(f'Key {key} not found')
را set() متد یک جفت کلید-مقدار به جدول اضافه می کند، در حالی که get() متد یک مقدار را با کلید خود بازیابی می کند. را remove() متد یک جفت کلید-مقدار را از جدول هش حذف می کند.
توجه داشته باشید: اگر کلید وجود نداشته باشد، get و remove روش ها را افزایش می دهد KeyError.
اکنون میتوانیم یک جدول هش ایجاد کنیم و از آن برای ذخیره و بازیابی دادهها استفاده کنیم:
hash_table = HashTable(10)
hash_table.set('Alice', 'January')
hash_table.set('Bob', 'May')
print(hash_table.get('Alice'))
hash_table.remove('Bob')
print(hash_table.get('Bob'))
توجه داشته باشید: اجرای جدول هش فوق بسیار ساده است و برخورد هش را مدیریت نمی کند. در استفاده در دنیای واقعی، به یک تابع هش پیچیدهتر و استراتژی حل برخورد نیاز دارید.
حل برخورد در جداول هش پایتون
برخورد هش بخش اجتناب ناپذیر استفاده از جداول هش است. تصادم هش زمانی رخ می دهد که دو کلید مختلف به یک شاخص در جدول هش هش کنند. از آنجایی که دیکشنری های پایتون پیاده سازی جداول هش هستند، به روشی برای مدیریت این برخوردها نیز نیاز دارند.
پیاده سازی جدول هش داخلی پایتون از روشی به نام استفاده می کند “آدرس باز” برای رسیدگی به برخوردهای هش با این حال، برای درک بهتر وضوح برخورد process، بیایید روش ساده تری به نام را مورد بحث قرار دهیم “زنجیره بندی جدا”.
زنجیربندی مجزا
زنجیربندی جداگانه یک روش حل تصادم است که در آن هر شکاف در جدول هش فهرست پیوندی از جفتهای کلید-مقدار را در خود دارد. هنگامی که یک برخورد رخ می دهد (یعنی دو کلید در یک شاخص هش می شوند)، جفت کلید-مقدار به سادگی به انتهای لیست پیوندی در نمایه در حال برخورد اضافه می شود.
به یاد داشته باشید، ما در مثال خود یک برخورد داشتیم زیرا هر دو "Bob" و "Brian" همین شاخص را داشت – 6. بیایید از آن مثال برای نشان دادن مکانیسم پشت زنجیرهای جداگانه استفاده کنیم. اگر بخواهیم فرض کنیم که "Bob" ابتدا عنصر به جدول هش اضافه شد، هنگام تلاش برای ذخیره آن با مشکل مواجه میشویم "Brian" عنصر از زمان شاخص 6 قبلا گرفته شده بود
حل این وضعیت با استفاده از زنجیره جداگانه شامل اضافه کردن "Brian" عنصر به عنوان دومین عنصر از لیست پیوندی اختصاص داده شده به فهرست 6 ( "Bob" عنصر اولین عنصر آن لیست است). و این تمام چیزی است که در آن وجود دارد، درست همانطور که در تصویر زیر نشان داده شده است:

در اینجا این است که چگونه می توانیم خود را اصلاح کنیم HashTable کلاس از مثال قبلی برای استفاده از زنجیره جداگانه:
class HashTable:
def __init__(self, size):
self.size = size
self.table = (() for _ in range(size))
def _hash(self, key):
return ord(key(0)) % self.size
def set(self, key, value):
hash_index = self._hash(key)
for kvp in self.table(hash_index):
if kvp(0) == key:
kvp(1) = value
return
self.table(hash_index).append((key, value))
def get(self, key):
hash_index = self._hash(key)
for kvp in self.table(hash_index):
if kvp(0) == key:
return kvp(1)
raise KeyError(f'Key {key} not found')
def remove(self, key):
hash_index = self._hash(key)
for i, kvp in enumerate(self.table(hash_index)):
if kvp(0) == key:
self.table(hash_index).pop(i)
return
raise KeyError(f'Key {key} not found')
در این پیاده سازی به روز شده، table به عنوان لیستی از لیست های خالی مقدار دهی اولیه می شود (یعنی هر شکاف یک لیست پیوندی خالی است). در set() روش، روی فهرست پیوندی در فهرست هش شده تکرار میکنیم و اگر کلید از قبل وجود داشته باشد، مقدار را بهروزرسانی میکنیم. اگر اینطور نیست، یک جفت کلید-مقدار جدید به لیست اضافه می کنیم.
را get() و remove() متدها همچنین باید روی فهرست پیوندی در فهرست هش شده تکرار شوند تا کلید مورد نظر خود را پیدا کنند.
در حالی که این رویکرد مشکل برخوردها را حل میکند، اما زمانی که برخوردها مکرر هستند، منجر به افزایش پیچیدگی زمانی میشود.
آدرس دهی را باز کنید
روشی که دیکشنریهای پایتون برای مدیریت برخوردها استفاده میکنند، پیچیدهتر از زنجیرهای جداگانه است. پایتون از نوعی آدرس دهی باز به نام استفاده می کند “کاوشگری”.
در کاوش، هنگامی که یک برخورد رخ می دهد، جدول هش شکاف موجود بعدی را بررسی می کند و به جای آن جفت کلید-مقدار را در آنجا قرار می دهد. را process یافتن اسلات موجود بعدی «کاوشگر» نامیده می شود و از چندین استراتژی می توان استفاده کرد، مانند:
- کاوش خطی – چک کردن یک اسلات در یک زمان به ترتیب
- کاوش درجه دوم – چک کردن اسلات در افزایش قدرت دو
توجه داشته باشید: روش خاصی که پایتون استفاده میکند پیچیدهتر از هر یک از اینها است، اما تضمین میکند که جستجوها، درجها و حذفها نزدیک به O (1) پیچیدگی زمانی حتی در مواردی که برخوردها مکرر هستند.
بیایید فقط نگاهی گذرا به مثال برخورد از بخش قبل بیندازیم و نشان دهیم که چگونه با استفاده از روش آدرس دهی باز با آن برخورد می کنیم. بگویید ما یک جدول هش داریم که فقط یک عنصر دارد – {"Bob", "May"} روی شماره شاخص 6. اکنون، ما نمی توانیم آن را اضافه کنیم "Brian" عنصر به جدول هش به دلیل برخورد. اما، مکانیسم کاوش خطی به ما می گوید که آن را در اولین شاخص خالی ذخیره کنیم – 7. همین، آسان است، درست است؟
نتیجه
جداول هش از زیربنای مفهومی تا اجرای آنها به عنوان فرهنگ لغت در پایتون، یکی از قدرتمندترین و همه کاره ترین ساختارهای داده است. آنها به ما اجازه میدهند تا دادهها را در برنامههایمان بهطور کارآمد ذخیره، بازیابی و دستکاری کنیم و آنها را برای بسیاری از برنامههای کاربردی دنیای واقعی مانند ذخیرهسازی، نمایهسازی دادهها، تجزیه و تحلیل فرکانس و موارد دیگر ارزشمند میسازند.
جدولهای هش مهارت خود را مدیون پیچیدگی زمانی خود هستند O (1) برای عملیات ضروری، آنها را حتی با حجم زیادی از داده ها بسیار سریع می کند. علاوه بر این، استراتژیهای حل برخورد آنها، مانند رویکرد آدرسدهی باز پایتون، تضمین میکند که برخوردها را به طور موثر مدیریت میکنند و کارایی خود را حفظ میکنند.
در حالی که دیکشنری ها، به عنوان پیاده سازی Python از جداول هش، قدرتمند و کارآمد هستند، آنها مصرف می کنند. حافظه بیشتر نسبت به سایر ساختارهای داده مانند لیست ها یا تاپل ها. این به طور کلی یک مبادله عادلانه برای مزایای عملکردی است که ارائه می دهند، اما اگر استفاده از حافظه یک نگرانی است (به عنوان مثال، اگر با مجموعه داده بسیار بزرگی کار می کنید)، باید به خاطر داشته باشید.
در چنین مواردی، ممکن است بخواهید جایگزینهایی مانند فهرستهای تاپل برای مجموعه دادههای کوچک یا ساختارهای داده کارآمدتر از نظر حافظه ارائه شده توسط کتابخانههایی مانند NumPy یا پانداها برای مجموعههای داده بزرگتر را در نظر بگیرید.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-30 22:03:06



