از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
روش های مونت کارلو چیست؟ چگونه آینده را با شبیه سازی پایتون پیش بینی کنیم
سرفصلهای مطلب
روش های مونت کارلو انقلابی در برنامه نویسی و مهندسی ایجاد کرده است.
این روشها از قدرت تصادفی بودن استفاده میکنند، که آنها را به ابزارهای مؤثری تبدیل میکند که به توسعهدهندگان کمک میکند تا مشکلات دشوار را در بسیاری از زمینهها حل کنند.
روشهای مونت کارلو در فیزیک، مالی، مهندسی و بسیاری از زمینههای دیگر که روشهای قطعی اغلب برای حل مسائل غیرعملی هستند، به کار گرفته شدهاند.
با روشهای مونت کارلو، شبیهسازیها و محاسبات بسیار پیچیده کارآمد و مدیریت آسان شدهاند.
انواع مختلفی از روش های مونت کارلو وجود دارد. اما همه آنها ایده استفاده از تصادفی برای تقریبی راه حل های مشکلات سخت را به اشتراک می گذارند. در این مقاله همه چیز را در مورد روش های مونت کارلو خواهید آموخت.
آنچه را پوشش خواهیم داد:
- درک روش های مونت کارلو از طریق یک قیاس
- روش های مونت کارلو چیست؟ راهنمای زبان انگلیسی ساده
- کاربردهای دنیای واقعی روش های مونت کارلو
- انواع روش های مونت کارلو
- پیاده سازی عملی: روش های مونت کارلو در پایتون
- آینده روش های مونت کارلو
پیش نیازها
برای درک همه چیز در این مقاله باید دانش اولیه ای از آمار داشته باشید.
اگر نیاز به مسواک زدن دارید روی مهارت های آماری خود را، توصیه می کنم این دوره freeCodeCamp را بررسی کنید:
درک روش های مونت کارلو از طریق یک قیاس

تصور کنید می خواهید ارتفاع متوسط درختان یک جنگل بزرگ را پیدا کنید.
اندازه گیری هر درخت غیرممکن و غیرعملی است. اما با روش های مونت کارلو می توان به صورت تصادفی چند نقطه از جنگل را انتخاب کرد و ارتفاع تمام درختان آن نقاط را اندازه گرفت.
با چندین بار انجام این کار و میانگین گیری همه این اندازه گیری ها، می توانیم میانگین ارتفاع همه درختان جنگل را تخمین بزنیم.
به این ترتیب، می توان با یافتن نمونه های کوچک و قابل مدیریت و میانگین گیری آنها، تخمین های بزرگی را در جمعیت های بزرگ و پیچیده انجام داد.
روش های مونت کارلو چیست؟ راهنمای زبان انگلیسی ساده

روشهای مونت کارلو نوعی الگوریتم رایانهای هستند که از اندازهگیریهای تصادفی مکرر برای به دست آوردن نتایج تقریبی برای یک مسئله معین استفاده میکنند.
آنها بخشی از حوزه ریاضی به نام تحلیل عددی هستند – استفاده از روش های تقریب برای یافتن راه حل هایی که روش های قطعی غیرعملی هستند.
ایده اصلی یافتن راهحلهای تقریبی کافی برای حل مشکلاتی است که حل مستقیم آنها خیلی سخت یا غیرممکن است.
این راه حل ها با به دست آوردن میانگین تعداد زیادی از نمونه های تصادفی انتخاب شده از جمعیت مسئله مورد نظر به دست می آیند.
به این ترتیب، در سیستم هایی با بسیاری از عوامل نامشخص و بخش های متقابل، روش های مونت کارلو قادر به ارائه بینشی در مورد روش رفتار و عملکرد سیستم هستند.
آنها مبتنی هستند روی ایده ریاضی قانون اعداد بزرگ در نظریه احتمال:
میانگین بسیاری از متغیرهای تصادفی مستقل و توزیع شده یکسان، در صورت وجود، به مقدار مورد انتظار همگرا می شود.
مشکل اصلی روشهای مونت کارلو کمبود منابع کامپیوتری برای انجام شبیهسازیهای زیاد برای رسیدن به نتایج خوب است.
چرا به آنها “مونته کارلو” می گویند؟
روشهای مونت کارلو، که از کازینو موناکو در موناکو نامگذاری شدهاند، توسط ریاضیدانان در خلال پروژه منهتن دهه ۱۹۴۰ ابداع شدند.
استانیسلاو اولام، جان فون نویمان و دیگران در این پروژه مشارکت داشتند که بمب هسته ای آمریکا را توسعه دادند.
این نام نشان دهنده تصادفی بودن شبیه سازی های آنها است، مشابه نتایج تصادفی در قمار کازینو.
کاربردهای دنیای واقعی روش های مونت کارلو
طراحی مدار در مهندسی برق

مدارها اجزای زیادی دارند. در اینجا به برخی از آنها اشاره می کنیم:
- مقاومت ها
- سلف ها
- خازن ها
- دیودها
- ترانزیستورها
به دلیل دمای محیطی که در آن قرار دارند، گاهی اوقات مدارها ممکن است کار نکنند.
بنابراین، مهندسان چگونه مدارهای مقاوم در برابر دما را طراحی می کنند؟
به عبارت دیگر: چگونه می توانیم عملکرد یک مدار را در دماهای مختلف آزمایش کنیم؟
به لطف روشهای مونت کارلو میتوانیم فواصل زیادی از شرایط دمایی را شبیهسازی کنیم و اثرات آنها را ببینیم روی اجزای مدار و میزان تاثیر آنها بر عملکرد مدار
از این طریق می توانیم داده ها را جمع آوری کنیم روی چگونه اجزاء باید تحت تنش های حرارتی مختلف عمل کنند.
به این ترتیب، ما میتوانیم مدار را – چه برای تغییر طراحی مدار یا انتخاب اجزای مختلف – برای کار در بسیاری از شرایط محیطی بهینه کنیم.
طراحی موشک در مهندسی هوافضا

طراحی موشک شامل متغیرهای مختلفی است، مانند:
- خواص مواد
- نیروهای آیرودینامیکی
- راندمان پیشرانه
- شرایط محیطی.
روشهای مونت کارلو امکان شبیهسازیهای متعدد با خواص مواد مختلف، راندمان نیروی محرکه و متغیرهای طراحی بیشتر را فراهم میکنند.
این به درک عمیق رفتار موشک در شرایط مختلف کمک می کند.
در اصل، این روش تصادفی برای حل یک مشکل بزرگ در درک رفتار احتمالی عملکرد موشک کلیدی است، مانند:
- مسیر حرکت
- ثبات
- تمامیت ساختاری
مهندسان با تجزیه و تحلیل اینکه چگونه این متغیرهای طراحی بر رفتار احتمالی معیارهای عملکرد مهم پرواز موشک تأثیر میگذارند، میتوانند موشکها را ایمنتر و قابل اعتمادتر کنند.
بهینه سازی پرتفوی مالی در امور مالی و سرمایه گذاری

در بهینه سازی پرتفوی مالی، بهترین ترکیب دارایی ها در یک سبد برای به حداکثر رساندن بازده و در عین حال به حداقل رساندن ریسک چیست؟
روشهای مونت کارلو برای شبیهسازی میزان خوب بودن یک سبد در به حداکثر رساندن بازده و در عین حال به حداقل رساندن ریسک در شرایط مختلف بازار استفاده میشوند.
با ایجاد سناریوهای تصادفی بسیاری برای قیمت و بازده دارایی ها، بانک ها و موسسات مالی می توانند تحت شرایط مختلف، نتایج پرتفوی را بدانند و ریسک را مدیریت کنند.
به این ترتیب، می توان تصمیمات مبتنی بر داده را برای یافتن تعادل بین ریسک و پاداش اتخاذ کرد.
بررسی انواع مختلف روش های مونت کارلو
انواع مختلفی از روش های مونت کارلو وجود دارد. در اینجا برخی از مهمترین آنها آورده شده است:
مونت کارلو کلاسیک:
مونت کارلو کلاسیک از نمونه های تصادفی برای تخمین مقادیر و شبیه سازی سیستم ها استفاده می کند. برای کارهایی که یافتن راهحلهای مستقیم دشوار است، مانند ادغام عددی، مفید است
مونت کارلو بیزی:
مونت کارلو بیزی تخمین ها را با استفاده از اطلاعات موجود با مشاهدات جدید برای پیش بینی های بهتر بهبود می بخشد.
این مونت کارلو بیزی نامیده می شود زیرا از قضیه بیز استفاده می کند.
قضیه بیز توسط ریاضیدان توماس بیز ایجاد شد و در نظریه احتمال بسیار مهم است.
ایده اصلی قضیه این است که باورهای موجود را با داده های جدید اصلاح کنید.
این روش زمانی ایده آل است که شما برخی اطلاعات موجود در مورد مشکل دارید.
مارکوف چین مونت کارلو (MCMC):
برای مجموعه دادههای بزرگ، روشهای مونت کارلو معمولاً برای محاسبه نتایج بسیار طولانی است.
یکی از راه های حل این مشکل استفاده از نسخه کوچکتر مجموعه داده های بزرگ است. این به نوعی مانند یک خلاصه است نشان می دهد محتوای یک کتاب چون سریعتر خوانده می شود.
این نسخه کوچکتر زنجیره مارکوف نامیده می شود.
به عبارت ساده، زنجیره های مارکوف مدل هایی هستند که نشان می دهند یک سیستم چگونه بین حالت ها حرکت می کند.
یک مجموعه داده بزرگ را می توان به عنوان یک سیستم و حالت ها را به عنوان الگوهای داده در نظر گرفت.
به این ترتیب، زنجیرهای مارکوف مدل های ساده ای هستند که می توانند نمایندگی کند یک مجموعه داده بزرگ زیرا نشان می دهد که چگونه چیزها از یک حالت به حالت دیگر تغییر می کنند.
این تغییر حالت می تواند با اعداد کمتر، الگوهای مهم در داده ها را نشان دهد.
به این ترتیب، از زنجیره مارکوف، روش مونت کارلو نتایج خود را محاسبه می کند.
در اصل، مونت کارلو پیش بینی های خود را انجام می دهد غیر مستقیم از داده های اصلی زنجیره مارکوف به عنوان یک پیش پردازش داده ها مرحله برای محاسبه نتایج مونت کارلو
در پایان، MCMC فقط یک روش مونت کارلو معمولی است اما از نظر محاسباتی بسیار کارآمدتر است.
انواع دیگر
روش های دیگر مانند گرادیان، نیمه گرادیان و شبه مونت کارلو تمرکز نیز روی کارایی محاسباتی اما در این مقاله فقط به دنبال برجسته کردن اهمیت روش های مونت کارلو در علم، مهندسی و برنامه نویسی هستم.
پیاده سازی عملی: روش های مونت کارلو در پایتون
در کد زیر روش پیاده سازی یک نوع MCMC در پایتون را خواهید دید.
من یک نوع محبوب MCMC به نام مونت کارلو همیلتونی (HMC) را نمایش خواهم داد.
همیلتونی نامیده می شود زیرا از مفاهیم مکانیک همیلتونی برای پیشنهاد حالت های جدید برای زنجیره های مارکوف در مرحله پیش پردازش داده ها استفاده می کند.
مکانیک هامیلتونی چیست؟
برای پاسخ به این سوال، باید کمی در مورد مکانیک کلاسیک بدانید.
مکانیک کلاسیک از قوانین حرکت نیوتن برای توضیح روش رفتار و تغییر سیستم های فیزیکی در طول زمان استفاده می کند.
مکانیک هامیلتونی روش دیگری برای بررسی این سیستم ها است. اغلب بر نقش انرژی و بقای آن با استفاده از متغیرهای مختلف مانند موقعیت های تعمیم یافته و لحظه ای تاکید می کند.
این روش منحصر به فرد برای توصیف وضعیت و تکامل یک سیستم در HMC استفاده می شود.
هدف مثال کد اصلی
ما یک توزیع هدف را از یک توزیع گاوسی دو بعدی با استفاده از TensorFlow Probability ایجاد خواهیم کرد. این بدان معناست که HMC این توزیع هدف را مدل خواهد کرد.
توزیع گاوسی دو بعدی با داده های مصنوعی برای نشان دادن تقریب ایجاد شده است process با استفاده از مونت کارلو همیلتونی
به عبارت دیگر، HMC این توزیع گاوسی دوبعدی را به طور دقیق نشان خواهد داد.
در سناریوهای واقعی، از مدارها تا امور مالی، همه سیستم ها را می توان به عنوان یک توزیع احتمال توصیف کرد.
روش های مونت کارلو این توزیع های پیچیده را تقریب می زند. و MCMC این را می سازد process بسیار سریعتر
در این مثال کد ساده، من یک توزیع هدف ساده را تقریب میزنم تا بتوانید درک کنید که در یک سناریوی واقعی چگونه این مورد اعمال میشود.
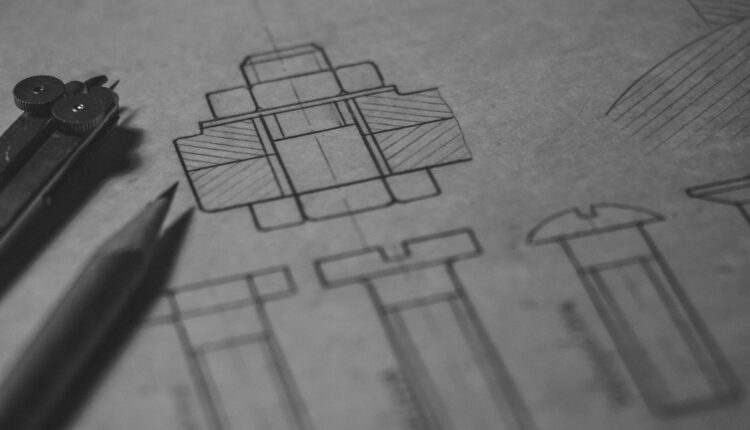
این کد کامل است (در زیر به صورت گام به گام آن را بررسی خواهیم کرد):
import tensorflow as tf
import tensorflow_probability as tfp
# Define the target distribution (2D Gaussian)
def target_log_prob(x, y):
return -0.5 * (x**2 + y**2)
# Initialize the HMC transition kernel
num_results = 1000
num_burnin_steps = 500
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=lambda x, y: target_log_prob(x, y),
num_leapfrog_steps=3,
step_size=0.1
)
# Define the trace function to record the state and kernel results
@tf.function
def run_chain(initial_state, kernel, num_results, num_burnin_steps):
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel,
trace_fn=lambda _, pkr: pkr
)
# Run the MCMC chain
initial_state = [tf.zeros([]), tf.zeros([])]
samples, kernel_results = run_chain(initial_state, hmc, num_results, num_burnin_steps)
# Extract the samples and log
samples_ = [s.numpy() for s in samples]
samples_x, samples_y = samples_
print("Acceptance rate: ", kernel_results.is_accepted.numpy().mean())
print("Mean of x: ", samples_x.mean())
print("Mean of y: ", samples_y.mean())
بیایید روش عملکرد کد را گام به گام درک کنیم.
کتابخانه ها را وارد کنید
import tensorflow as tf
import tensorflow_probability as tfp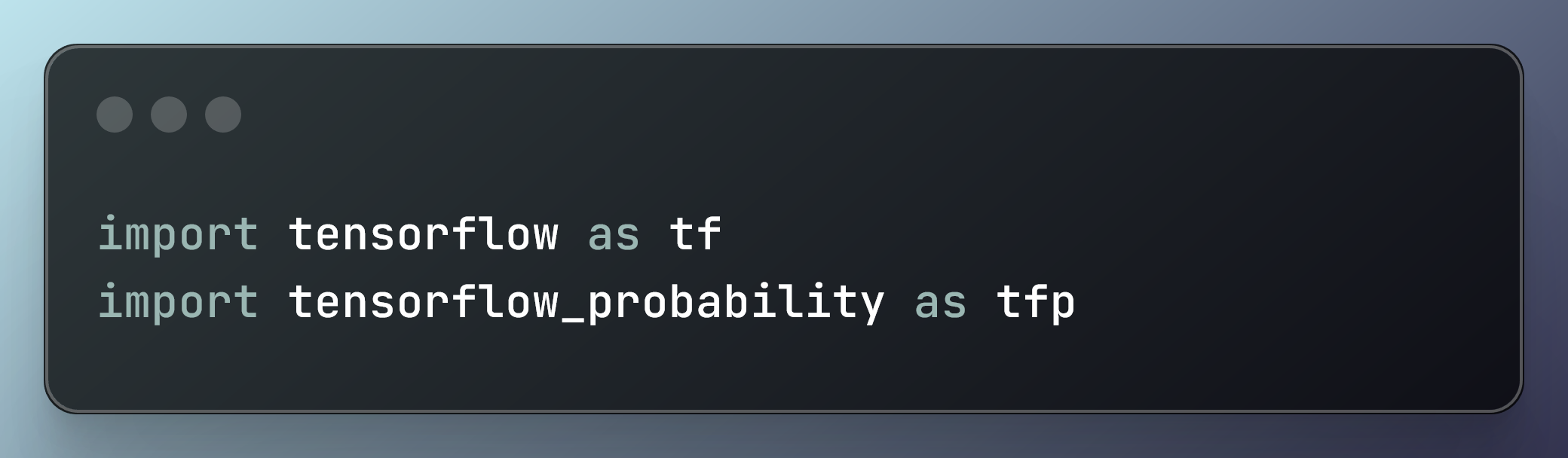
در این کد ما import دو کتابخانه پایتون:
- TensorFlow: ساخت و آموزش مدل های یادگیری ماشین
- TensorFlow Probability: استدلال احتمالی و مدل سازی آماری
یک توزیع هدف ایجاد کنید
def target_log_prob(x, y):
return -0.5 * (x**2 + y**2)
در این کد، توزیع گاوسی دوبعدی را تعریف می کنیم:
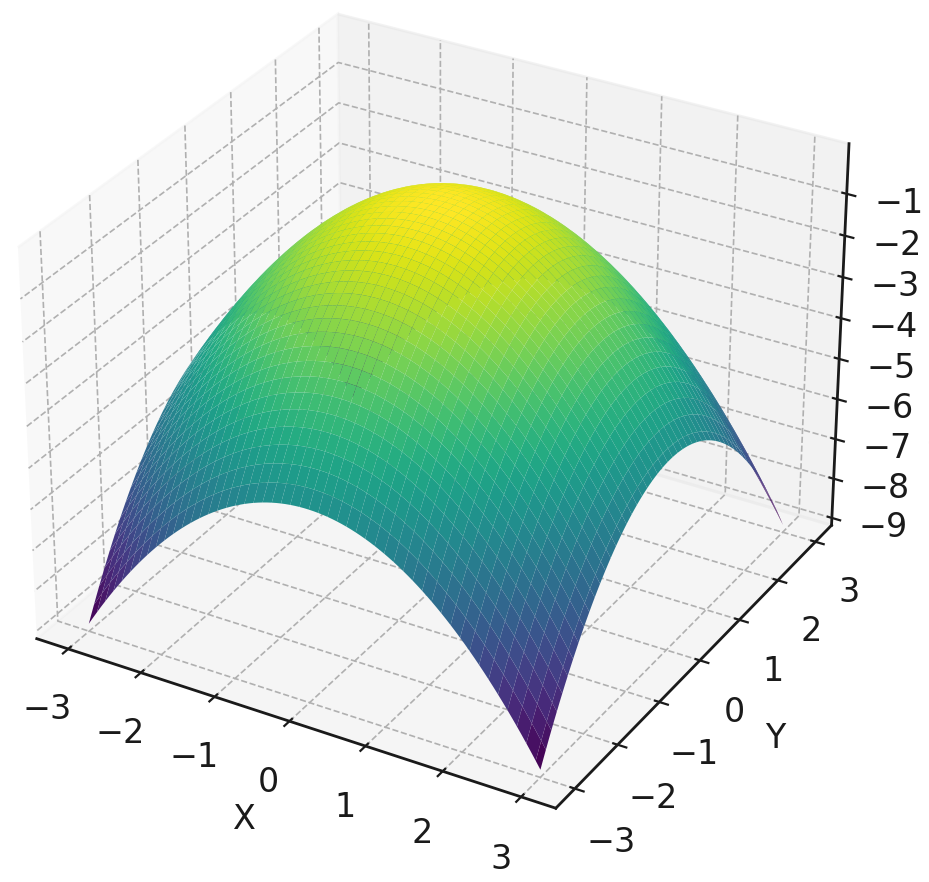
این نمودار به صورت زیر تعریف می شود:
-0.5 × (x2 + y2)
از آنجایی که یک توزیع گاوسی دوبعدی است، هر نقطه داده با دو متغیر همبسته که از یک توزیع گاوسی مشترک پیروی می کنند، نشان داده می شود.
اگر این یک سناریوی واقعی بود، ما یک سیستم را با پیدا کردن توزیع احتمال آن بر اساس مدل سازی می کردیم. روی دو متغیر
در بسیاری از کاربردهای عملی، مانند مدارها، ده ها متغیر می توانند دخیل باشند.
برای مدلسازی صحیح چنین سیستمهایی، اغلب از توزیعهای احتمال چند متغیره استفاده میکنیم که مفهوم توزیع گاوسی را به بسیاری از ابعاد تعمیم میدهد.
زنجیره مارکوف مونت کارلو را راه اندازی کنید
num_results = 1000
num_burnin_steps = 500
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=lambda x, y: target_log_prob(x, y),
num_leapfrog_steps=3,
step_size=0.1
)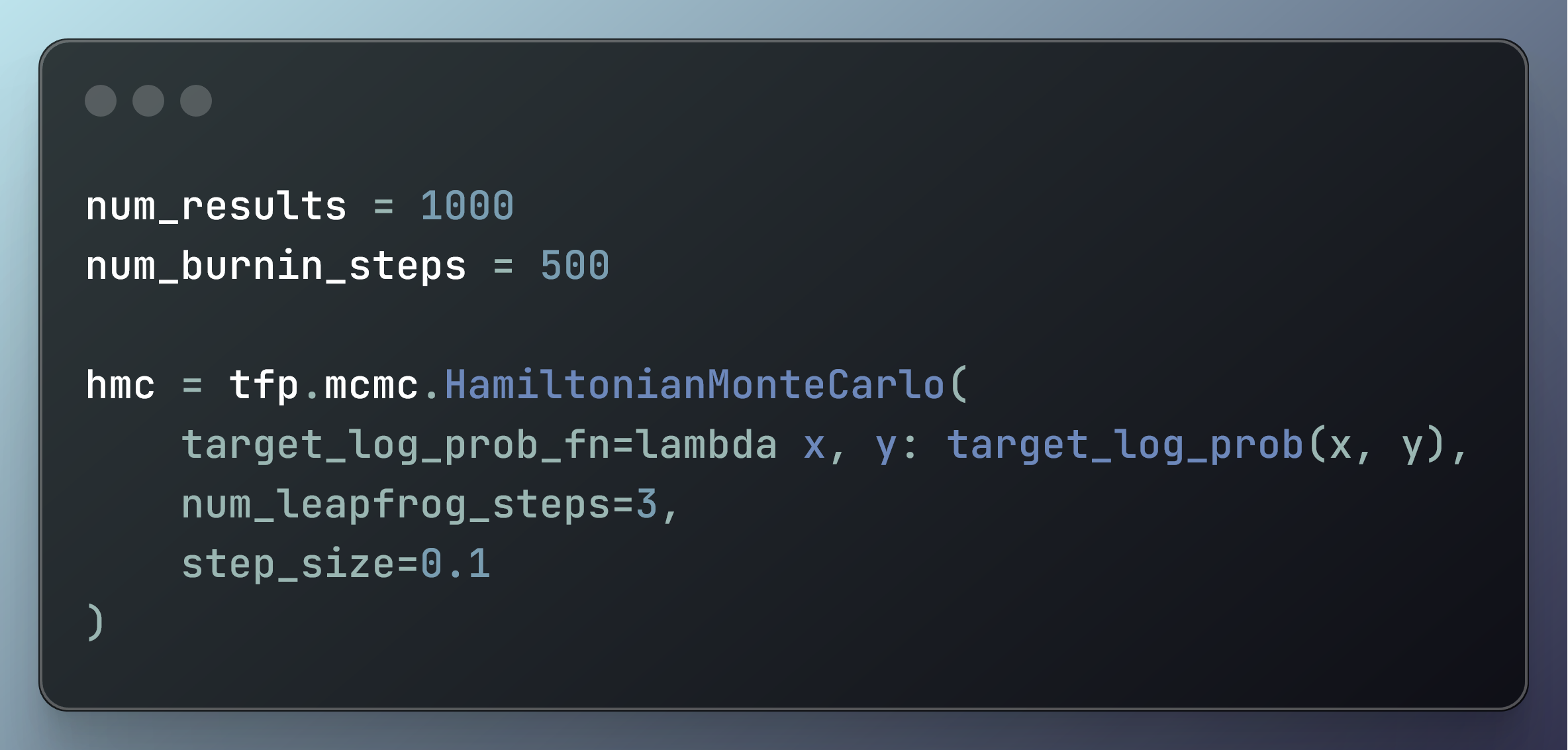
این بلوک کد یک هسته انتقال همیلتونی مونت کارلو (HMC) را با استفاده از TensorFlow Probability تنظیم می کند.
ابتدا دو متغیر را تعریف می کند:
num_resultsبه عنوان 1000، نشان دهنده تعداد نمونه های تولید شده استnum_burnin_stepsبه عنوان 500، نشان دهنده تعداد نمونه های اولیه برای دور ریختن (دوره سوختگی).
هسته انتقال HMC با:
- یک تابع احتمال لاگ هدف که دو ورودی را می گیرد و احتمال لاگ آنها را برمی گرداند. در مورد ما، تابع احتمال ورود به سیستم هدف توزیع گاوسی دوبعدی است. احتمال ورود به سیستم، احتمال وجود مجموعه خاصی از مقادیر است.
- الگوریتم هر بار 3 مرحله انجام می دهد.
- اندازه هر مرحله (تغییر مقدار) 0.1 است.
برای ثبت وضعیت و نتایج هسته، تابع trace را ایجاد کنید
@tf.function
def run_chain(initial_state, kernel, num_results, num_burnin_steps):
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel,
trace_fn=lambda _, pkr: pkr
)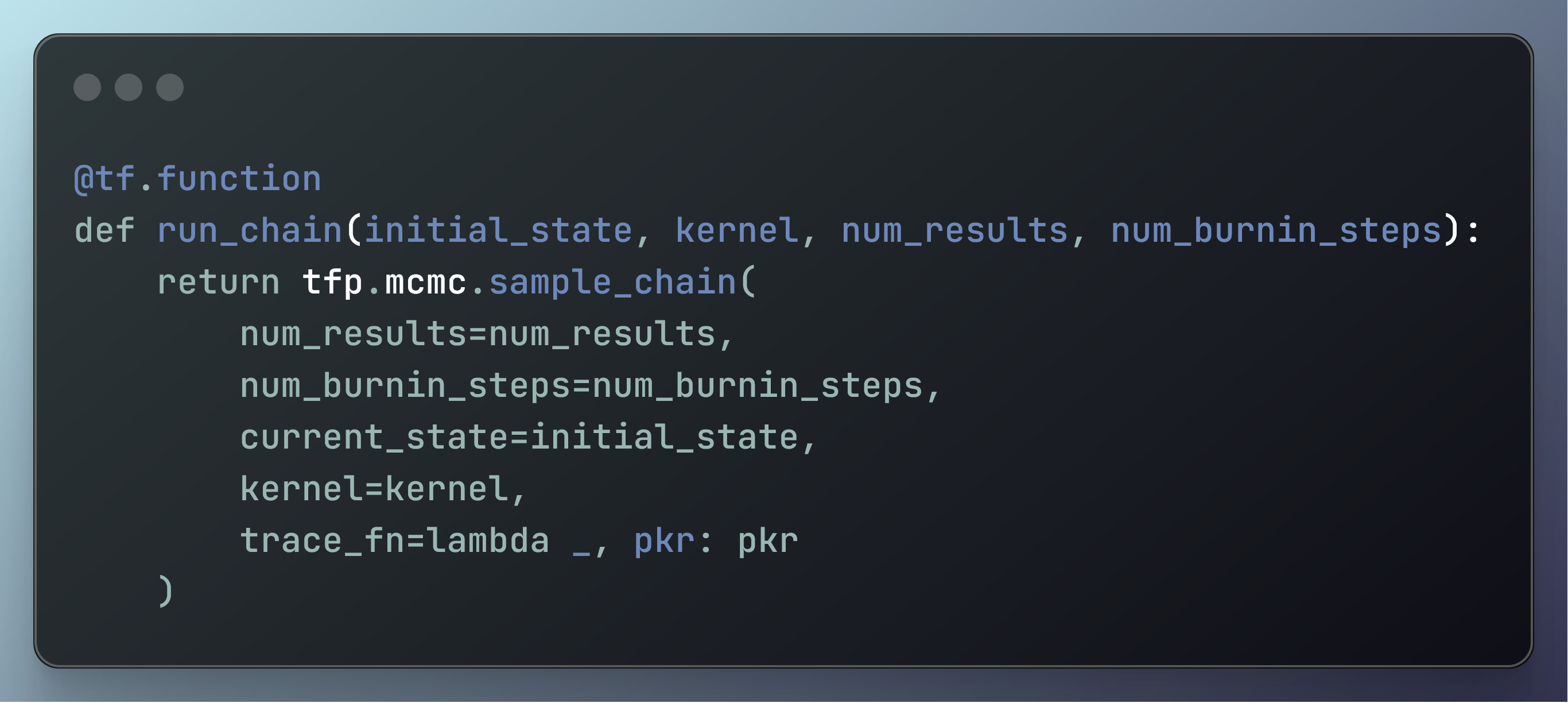
عملکرد با تزئین شده است @tf.function، که با کامپایل کردن آن در یک نمودار TensorFlow، آن را برای عملکرد بهینه می کند.
کارکرد run_chain چهار استدلال می گیرد:
initial_state: حالت اولیه زنجیره مارکوف.kernel: هسته انتقال MCMC برای استفاده (مانند مونت کارلو همیلتونی).num_results: تعداد نمونه هایی که باید تولید شوند.num_burnin_steps: تعداد نمونه های اولیه برای دور ریختن (دوره سوختگی).
تابع فراخوانی می کند tfp.mcmc.sample_chain برای انجام نمونه برداری MCMC:
num_results: تعداد نمونه هایی که باید رسم شوند.num_burnin_steps: تعداد مراحل سوختن.current_state: حالت شروع زنجیره مارکوف.kernel: هسته انتقالی که نمونه برداری را تعریف می کند process.trace_fn: تابعی که مشخص می کند در طول نمونه برداری چه چیزی را ردیابی کنیم. در این حالت، نتایج هسته قبلی را برمی گرداند (pkr) به طور موثر وضعیت داخلی الگوریتم MCMC را ردیابی می کند.
زنجیره MCMC را اجرا کنید
# Run the MCMC chain
initial_state = [tf.zeros([]), tf.zeros([])]
samples, kernel_results = run_chain(initial_state, hmc, num_results, num_burnin_steps)
# Extract the samples and log
samples_ = [s.numpy() for s in samples]
samples_x, samples_y = samples_
print("Acceptance rate: ", kernel_results.is_accepted.numpy().mean())
print("Mean of x: ", samples_x.mean())
print("Mean of y: ", samples_y.mean())
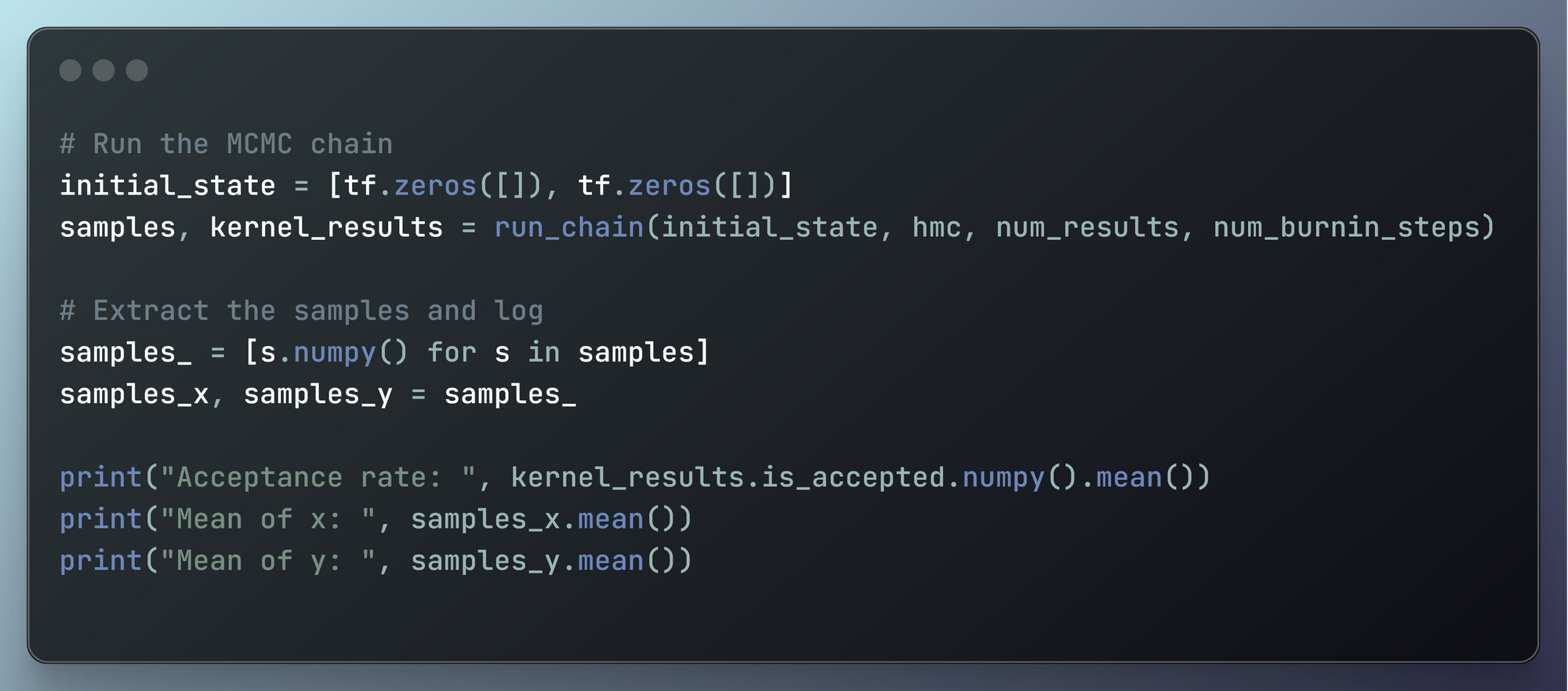
بسیار خوب، بیایید این را تجزیه کنیم زیرا چیزهای زیادی در حال انجام است روی اینجا:
دولت را راه اندازی کنید:
initial_stateبه لیستی شامل دو تانسور صفر تنظیم شده است که به عنوان نقطه شروع زنجیره مارکوف عمل می کند.
زنجیره MCMC را اجرا کنید:
- این
run_chainتابع با حالت اولیه، هسته HMC، تعداد نتایج و تعداد مراحل رایت فراخوانی می شود. - تابع دو مقدار برمی گرداند:
samples، که نمونه های تولید شده هستند وkernel_results، که حاوی نتایج حاصل از هسته (شامل اطلاعات تشخیصی) است.
استخراج و تبدیل نمونه ها:
- نمونه ها از تانسورهای TensorFlow به آرایه های NumPy برای دستکاری و تجزیه و تحلیل آسان تر تبدیل می شوند.
samples_یک لیست درک است که هر تانسور نمونه را به یک آرایه numpy تبدیل می کند.samples_xوsamples_yنمونه های استخراج شده برای دو بعد هستند.
تشخیص چاپ:
- میزان پذیرش نمونهبردار MCMC محاسبه و چاپ میشود. نسبت پیشنهادات پذیرفته شده را در طول نمونه گیری نشان می دهد.
- میانگین نمونه ها برای هر دو بعد (
xوy) برای ارائه خلاصه ای از نتایج نمونه گیری محاسبه و چاپ می شوند.
این به عنوان نتایج نشان می دهد:
- نرخ پذیرش: 1.0. این بدان معناست که تمام پیشنهادات ارائه شده در طول نمونه گیری پذیرفته شد
- میانگین x: -0.11450629 و میانگین y: -0.23079416. در یک توزیع گاوسی کامل دو بعدی، میانگین x و y 0 است.
با این نوع MCMC، توزیع گاوسی دوبعدی را تقریب میکنیم. اما نزدیک به صفر است. این بدان معنی است که با توجه به زمان محاسباتی بیشتر، احتمالاً تا زمانی که آنقدر کوچک باشد که بتوان آن را صفر در نظر گرفت، به عدد کوچکتری میرود.
نتیجه گیری: آینده روش های مونت کارلو
آینده روش های مونت کارلو در ایجاد انواعی نهفته است که به منابع محاسباتی کمتری نیاز دارند و در زمان صرفه جویی می کنند.
با این پیشرفت ها، روش های مونت کارلو کاربردهای بیشتری در زمینه های بیشتری پیدا می کند.
به لطف روشهای مونت کارلو، ما میتوانیم سیستمها و پدیدههای پیچیدهای را که قبلاً انجام آنها غیرممکن بود به روشی کارآمد مدلسازی کنیم.
اگر می خواهید بیشتر بدانید، می توانید این مقاله را بخوانید روی روش های مونت کارلو
همچنین می توانید کد کامل را در اینجا بررسی کنید:
منتشر شده در 1403-07-17 11:20:05



