از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
جستجوی خطی در پایتون
سرفصلهای مطلب
معرفی
جستجوی خطی، همچنین به عنوان شناخته شده است جستجوی متوالی، با عبور از مجموعه داده، عنصر به عنصر تا زمانی که مورد مورد نظر پیدا شود یا الگوریتم به انتهای مجموعه برسد عمل می کند. سادگی و سهولت اجرای آن، آن را برای مجموعههای داده کوچک و فهرستهایی که آیتمها مرتباً اضافه یا حذف میشوند، انتخابی مناسب میسازد.
اگرچه ممکن است کارایی مشابه های پیچیده تر خود مانند جستجوی باینری را نداشته باشد، جستجوی خطی می تواند در موارد استفاده عملی مختلف بسیار مفید باشد، به خصوص زمانی که با داده های مرتب نشده سروکار دارید.
در این مقاله، ما عمیقتر به عملکرد درونی جستجوی خطی میپردازیم، مکانیسم آن را با مثالهای کاربردی پایتون نشان میدهیم، و عملکرد آن را از طریق تحلیل پیچیدگی تشریح میکنیم.
جستجوی خطی چگونه کار می کند؟
جستجوی خطی، همانطور که از نام آن پیداست، به روشی ساده و خطی عمل می کند و به طور سیستماتیک هر عنصر در مجموعه داده را بررسی می کند تا زمانی که مورد مورد نظر قرار گیرد یا به انتهای مجموعه داده برسد. این نیازی ندارد که داده ها به ترتیب خاصی باشند و با هر دو مجموعه داده مرتب شده و مرتب نشده به خوبی کار می کند.
بیایید عملکرد آن را به یک تقسیم کنیم فرآیند گام به گام:
-
از ابتدا شروع کنید
- جستجوی خطی از اولین عنصر مجموعه داده شروع می شود. مقدار هدف (مقداری که در جستجوی آن هستیم) با عنصر اول مقایسه می کند.
-
مقایسه و جابجایی
- اگر مقدار هدف با عنصر فعلی مطابقت دارد، تبریک میگوییم! جستجو موفقیت آمیز است و شاخص (یا موقعیت) عنصر فعلی برگردانده می شود. اگر مطابقت پیدا نشد، الگوریتم به عنصر بعدی در دنباله منتقل می شود.
-
تکرار
- این فرآیند حرکت از یک عنصر به عنصر بعدی و مقایسه هر یک با مقدار هدف به صورت متوالی از طریق مجموعه داده ادامه می یابد.
-
نتیجه گیری جستجو
-
مورد پیدا شد: اگر الگوریتم عنصری را پیدا کند که با مقدار هدف مطابقت دارد، شاخص آن عنصر را برمیگرداند.
-
مورد پیدا نشد: اگر الگوریتم بدون یافتن مقدار هدف به پایان مجموعه داده برسد، نتیجه می گیرد که مورد در مجموعه داده وجود ندارد و معمولاً مقداری را نشان می دهد که جستجوی ناموفق را نشان می دهد (مانند
-1یاNoneدر پایتون).
-
جستجوی خطی به دلیل سادگی و این واقعیت که می تواند در مجموعه داده های مرتب شده و مرتب نشده استفاده شود، بسیار مفید است.
توجه داشته باشید: سادگی آن می تواند یک شمشیر دو لبه، به ویژه با مجموعه داده های بزرگ، زیرا ممکن است مجبور باشد از بیشتر عناصر عبور کند و در مقایسه با سایر الگوریتم های جستجو در سناریوهای خاص کارآمدتر شود.
جستجوی خطی – مثال
اکنون که فهمیدیم جستجوی خطی در تئوری چگونه کار می کند، بیایید یک مثال ملموس را برای تجسم عملکرد آن بررسی کنیم. فرض کنید ما در حال جستجوی لیست اعداد زیر هستیم:
numbers = (21, 39, 46, 52, 63, 75)
و فرض کنید می خواهیم شماره را پیدا کنیم 52:
- مرحله 1: با شماره اول شروع کنید –
21- مقایسه کنید با
52– آن ها هستند نا برابر
- مقایسه کنید با
- گام 2: به شماره بعدی بروید –
39- مقایسه کنید با
52– هنوز نا برابر
- مقایسه کنید با
- مرحله 3: به شماره بعدی بروید –
46- مقایسه کنید با
52– نا برابر
- مقایسه کنید با
- مرحله 4: به شماره بعدی بروید –
52- سرانجام، آنها برابر هستند!
- شاخص را برگردانید
3به عنوان نتیجه جستجوی موفق
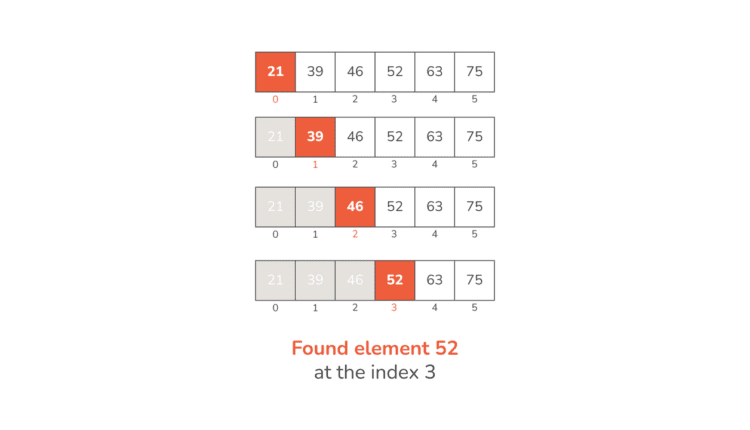
تصویر زیر به صورت بصری فرآیندی را که ما توضیح دادیم نشان می دهد:

در بخشهای آینده، به دنیای پایتونیک میپردازیم تا جستجوی خطی را پیادهسازی کنیم و پیچیدگی آن را از نظر زمان و مکان بررسی کنیم تا کارایی و محدودیتهای آن را درک کنیم.
نحوه پیاده سازی جستجوی خطی در پایتون
پس از بررسی چارچوب مفهومی و گذراندن نمونهای از جستجوی خطی، بیایید برای پیادهسازی این الگوریتم وارد پایتون شویم.
اول از همه، ما تابعی را تعریف می کنیم که منطق جستجوی خطی را در بر می گیرد – بیایید آن را فراخوانی کنیم. linear_search(). باید دو پارامتر داشته باشد – arr (لیست برای جستجو) و target (مورد جستجو):
def linear_search(arr, target):
اکنون، این تابع یک جستجوی خطی در یک لیست انجام می دهد arr برای یک target ارزش. باید ایندکس را برگرداند target که در arr اگر پیدا شد، و -1 در غیر این صورت.
ما در نهایت میتوانیم به هسته الگوریتم جستجوی خطی برسیم – حلقه زدن در لیست و مقایسه عنصر فعلی با target. ما این کار را با تکرار از طریق هر عنصر انجام خواهیم داد item و مربوط به آن index در لیست arr با استفاده از enumerate تابع:
def linear_search(arr, target):
for index, item in enumerate(arr):
if item == target:
return index # Target found, return the index
return -1 # Target not found, return -1
توجه داشته باشید: با استفاده از for حلقه ها بدون اعمال نفوذ توابع داخلی مانند enumerate می تواند منجر به کد خوانا و بالقوه کمتر کارآمد شود.
از خودمان استفاده کنیم linear_search() تابع برای یافتن یک مورد در یک لیست:
books = ("The Great Gatsby", "Moby Dick", "1984", "To Kill a Mockingbird", "The Hobbit")
target_book = "1984"
# Using the linear_search function
index = linear_search(books, target_book)
# Output the result
if index != -1:
print(f"'{target_book}' found at index {index}.")
else:
print(f"'{target_book}' not found in the list.")
این منجر به:
'1984' found at index 2.
توجه داشته باشید: این پیاده سازی Python از جستجوی خطی ساده و مبتدی است و ابزاری عملی برای جستجوی موارد در یک لیست ارائه می دهد.
در بخشهای آینده، به تحلیل پیچیدگی جستجوی خطی میپردازیم، کارایی آن را بررسی میکنیم و در مورد سناریوهایی بحث میکنیم که کجا میدرخشد و دیگر الگوریتمها ممکن است مناسبتر باشند.
تحلیل پیچیدگی
درک پیچیدگی یک الگوریتم بسیار مهم است زیرا بینش هایی را در مورد کارایی آن از نظر زمان و مکان ارائه می دهد و در نتیجه به توسعه دهندگان اجازه می دهد هنگام انتخاب الگوریتم ها برای زمینه های خاص تصمیمات آگاهانه بگیرند. بیایید پیچیدگی جستجوی خطی را تشریح کنیم:
پیچیدگی زمانی
این بهترین سناریو زمانی اتفاق می افتد که عنصر هدف در اولین موقعیت آرایه پیدا شود. در این مورد، تنها یک مقایسه انجام می شود که منجر به پیچیدگی زمانی می شود O (1). این بدترین حالت سناریو زمانی اتفاق میافتد که عنصر هدف در آخرین موقعیت آرایه باشد یا اصلاً وجود نداشته باشد. در اینجا، الگوریتم می سازد n مقایسه ها، کجا n اندازه آرایه است که منجر به پیچیدگی زمانی می شود بر). به طور متوسط، ممکن است الگوریتم مجبور باشد نیمی از عناصر را جستجو کند و در نتیجه پیچیدگی زمانی ایجاد شود O(n/2). با این حال، در نماد O بزرگ، عامل ثابت را رها می کنیم و ما را کنار می گذاریم بر).
پیچیدگی فضا
جستجوی خطی یک الگوریتم در محل، به این معنی که به فضای اضافی که با اندازه ورودی بزرگ می شود نیاز ندارد. از مقدار ثابتی از فضای اضافی استفاده می کند (برای متغیرهایی مانند index و item) و بنابراین، پیچیدگی فضا است O (1).
در چارچوب کاربردهای عملی، جستجوی خطی می تواند در سناریوهایی که در آن سادگی اجرا در اولویت است، و مجموعه داده های درگیر هستند زیاد بزرگ نیست. با این حال، برای برنامههایی که عملیات جستجو مکرر هستند یا مجموعه دادهها بزرگ هستند، در نظر گرفتن الگوریتمهایی با پیچیدگی زمانی کمتر ممکن است مفید باشد.
جستجوی خطی در مقابل جستجوی باینری
جستجوی خطی با سادگی و سهولت پیاده سازی، جایگاه منحصر به فردی در دنیای الگوریتم های جستجو دارد. با این حال، بسته به زمینه، سایر الگوریتمهای جستجو ممکن است کارآمدتر یا مناسبتر باشند. بیایید به تجزیه و تحلیل مقایسه ای بین جستجوی خطی و رقیب اصلی آن در فضای الگوریتم های جستجو – جستجوی باینری بپردازیم.
| جستجوی خطی | جستجوی باینری | |
|---|---|---|
| پیش نیازها | هیچ پیش نیازی در مورد ترتیب مجموعه داده وجود ندارد. | نیاز به مرتب سازی مجموعه داده دارد. |
| پیچیدگی زمانی | O(n) در بدترین و متوسط ترین موارد. | O(logn) در بدترین و متوسط ترین موارد. |
| موارد استفاده | مناسب برای مجموعه داده های کوچکتر و/یا نامرتب. | ایده آل برای مجموعه داده های بزرگتر و مرتب شده، به ویژه در جاهایی که عملیات جستجو مکرر است. |
| پیاده سازی | پیاده سازی ساده تر | به دلیل نیاز به مدیریت نشانگرهای بالا و پایین در طول جستجو کمی پیچیده تر است. |
نتیجه
جستجوی خطی با سادگی و حداقل پیشنیازها متمایز است و اغلب به ابزاری برای سناریوهایی تبدیل میشود که در آن سادگی کلیدی است و مجموعه داده بیش از حد بزرگ نیست. صراحت آن می تواند در بسیاری از موقعیت های برنامه نویسی عملی، ارزشمندتر از کارایی محاسباتی باشد، به ویژه برای مبتدیان یا در برنامه هایی که اندازه داده ها الگوریتم پیچیده تری را تضمین نمی کند.
علاوه بر این، جستجوی خطی فقط یک ابزار نیست – یک پله آموزشی در قلمرو الگوریتمها است. این یک درک اساسی برای تازه واردان ایجاد می کند، و یک پایه محکم ارائه می دهد که از طریق آن می توان پیچیدگی های الگوریتم های پیشرفته تر را رمزگشایی و قدردانی کرد.
در نتیجه، بسیار مهم است که تأکید کنیم انتخاب الگوریتم عمیقاً در زمینه ریشه دارد. جستجوی خطی، در سادگی ساده خود، راه حلی قابل اعتماد و قابل اجرا را برای انواع نیازهای جستجو ارائه می دهد.
منتشر شده در 1402-12-26 04:21:05



