از طریق منوی جستجو مطلب مورد نظر خود در وبلاگ را به سرعت پیدا کنید
DBSCAN با Scikit-Learn در پایتون
سرفصلهای مطلب
معرفی
شما در یک شرکت مشاوره به عنوان دانشمند داده کار می کنید. پروژه ای که در حال حاضر به آن منصوب شده اید دارای داده هایی از دانش آموزانی است که به تازگی دوره های مالی را به پایان رسانده اند. شرکت مالی که دورهها را برگزار میکند میخواهد بفهمد که آیا عوامل مشترکی وجود دارد که دانشجویان را برای خرید دورههای مشابه یا خرید دورههای مختلف تحت تأثیر قرار میدهد. با درک این عوامل، شرکت می تواند یک نمایه دانشجو ایجاد کند، هر دانش آموز را بر اساس مشخصات طبقه بندی کند و لیستی از دوره ها را توصیه کند.
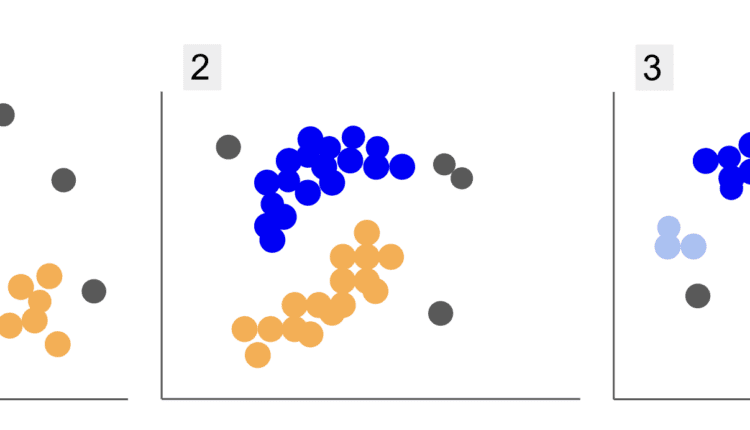
هنگام بررسی دادههای گروههای دانشجویی مختلف، با سه حالت از نکات روبرو شدهاید، مانند 1، 2 و 3 زیر:

توجه کنید که در نمودار 1، نقاط بنفش در یک نیم دایره سازماندهی شده اند، با توده ای از نقاط صورتی در داخل آن دایره، غلظت کمی از نقاط نارنجی در خارج از آن نیم دایره، و پنج نقطه خاکستری که از همه نقاط دیگر دور هستند.
در نمودار 2، یک توده گرد از نقاط بنفش، دیگری از نقاط نارنجی، و همچنین چهار نقطه خاکستری وجود دارد که از بقیه نقاط دور هستند.
و در نمودار 3 می توانیم چهار غلظت نقطه بنفش، آبی، نارنجی، صورتی و سه نقطه خاکستری دورتر را ببینیم.
حال، اگر بخواهید مدلی را انتخاب کنید که بتواند دادههای دانشآموز جدید را درک کند و گروههای مشابه را تعیین کند، آیا الگوریتم خوشهبندی وجود دارد که بتواند نتایج جالبی را به این نوع دادهها بدهد؟
هنگام توصیف طرح ها، اصطلاحاتی مانند توده نقاط و تمرکز نقاط، نشان می دهد که در تمام نمودارها مناطقی با چگالی بیشتر وجود دارد. ما نیز اشاره کردیم گرد و نیم دایره اشکالی که تشخیص آنها با کشیدن یک خط مستقیم یا صرفاً بررسی نزدیکترین نقاط دشوار است. علاوه بر این، نقاط دوردستی وجود دارد که احتمالاً از توزیع اصلی داده منحرف میشود و چالشهای بیشتری را معرفی میکند یا سر و صدا هنگام تعیین گروه ها
یک الگوریتم مبتنی بر چگالی که می تواند نویز را فیلتر کند، مانند DBSCAN (Dذات-بآسید اسصمیمی سیبراق شدن از آبرنامه های کاربردی با نoise)، یک انتخاب قوی برای موقعیت هایی با مناطق متراکم تر، شکل های گرد و نویز است.
درباره DBSCAN
DBSCAN یکی از الگوریتم های مورد استناد در تحقیقات است، اولین انتشار آن در سال 1996 ظاهر شد. کاغذ DBSCAN اصلی. در این مقاله، محققان نشان میدهند که چگونه این الگوریتم میتواند خوشههای فضایی غیرخطی را شناسایی کند و دادههای با ابعاد بالاتر را به طور کارآمد مدیریت کند.
ایده اصلی پشت DBSCAN این است که حداقل تعداد نقاطی وجود دارد که در یک فاصله یا فاصله مشخص قرار دارند شعاع از “مرکزی ترین” نقطه خوشه، نامیده می شود نقطه اصلی. نقاطی که در آن شعاع قرار دارند، نقاط همسایگی و نقاط هستند روی لبه آن محله هستند نقاط مرزی یا نقاط مرزی. شعاع یا فاصله همسایگی نامیده می شود محله اپسیلون، ε-محله یا فقط ε (نماد حرف یونانی اپسیلون).
علاوه بر این، زمانی که نقاطی وجود داشته باشند که نقاط اصلی یا نقاط مرزی نیستند، زیرا از شعاع تعلق به یک خوشه تعیینشده فراتر میروند و حداقل تعداد نقاط را برای یک نقطه مرکزی ندارند، در نظر گرفته میشوند. نقاط نویز.
این بدان معناست که ما سه نوع نقطه مختلف داریم، یعنی، هسته، مرز و سر و صدا. علاوه بر این، توجه به این نکته مهم است که ایده اصلی اساساً مبتنی است روی یک شعاع یا فاصله، که DBSCAN را – مانند اکثر مدل های خوشه بندی – وابسته می کند روی آن متریک فاصله این معیار می تواند اقلیدسی، منهتن، ماهالانوبیس و بسیاری موارد دیگر باشد. بنابراین، انتخاب یک متریک فاصله مناسب که زمینه داده ها را در نظر می گیرد بسیار مهم است. به عنوان مثال، اگر از دادههای مسافت رانندگی از طریق GPS استفاده میکنید، ممکن است استفاده از معیاری که طرحبندی خیابانها را در نظر میگیرد، مانند فاصله منهتن، جالب باشد.

توجه داشته باشید: از آنجایی که DBSCAN نقاطی که نویز را تشکیل می دهند را ترسیم می کند، می توان از آن به عنوان یک الگوریتم تشخیص بیرونی نیز استفاده کرد. برای مثال، اگر میخواهید تعیین کنید کدام تراکنشهای بانکی ممکن است تقلبی باشند و نرخ تراکنشهای جعلی کم باشد، DBSCAN ممکن است راهحلی برای شناسایی آن نقاط باشد.
برای یافتن نقطه اصلی، DBSCAN ابتدا یک نقطه را به صورت تصادفی انتخاب می کند، تمام نقاط درون همسایگی ε آن را ترسیم می کند و تعداد همسایگان نقطه انتخاب شده را با حداقل تعداد نقاط مقایسه می کند. اگر نقطه انتخاب شده دارای تعداد مساوی یا همسایه های بیشتر از حداقل تعداد امتیاز باشد، به عنوان نقطه اصلی علامت گذاری می شود. این نقطه مرکزی و نقاط همسایگی آن اولین خوشه را تشکیل خواهند داد.
سپس الگوریتم هر نقطه از اولین خوشه را بررسی می کند و می بیند که آیا تعداد نقاط همسایه آن برابر است یا بیشتر از حداقل تعداد نقاط درون ε. در این صورت، آن نقاط همسایه نیز به اولین خوشه اضافه خواهند شد. این process تا زمانی ادامه می یابد که نقاط خوشه اول دارای همسایگان کمتری نسبت به حداقل تعداد نقاط درون ε باشند. وقتی این اتفاق میافتد، الگوریتم اضافه کردن نقاط به آن خوشه را متوقف میکند، نقطه هسته دیگری را خارج از آن خوشه شناسایی میکند و یک خوشه جدید برای آن نقطه هسته جدید ایجاد میکند.
سپس DBSCAN اولین خوشه را تکرار می کند process یافتن تمام نقاط متصل به یک نقطه هسته جدید از خوشه دوم تا زمانی که هیچ نقطه دیگری به آن خوشه اضافه نشود. سپس با یک نقطه اصلی دیگر روبرو می شود و یک خوشه سوم ایجاد می کند، یا در تمام نقاطی که قبلاً به آنها نگاه نکرده است، تکرار می شود. اگر این نقاط در فاصله ε از یک خوشه باشند، به آن خوشه اضافه می شوند و به نقاط مرزی تبدیل می شوند. اگر اینطور نباشند، نقاط نویز محسوب می شوند.
جالب است بدانید که الگوریتم DBSCAN چگونه کار می کند، اگرچه خوشبختانه، زمانی که کتابخانه Scikit-Learn پایتون از قبل پیاده سازی داشته باشد، نیازی به کدگذاری الگوریتم نیست.
بیایید ببینیم در عمل چگونه کار می کند!
وارد کردن داده ها برای خوشه بندی
برای اینکه ببینیم DBSCAN در عمل چگونه کار میکند، پروژهها را کمی تغییر میدهیم و از مجموعه دادههای مشتری کوچکی استفاده میکنیم که دارای ژانر، سن، درآمد سالانه و امتیاز هزینههای 200 مشتری است.
امتیاز هزینه از 0 تا 100 متغیر است و نشان می دهد که یک فرد چقدر پول در یک مرکز خرید خرج می کند. روی یک مقیاس از 1 تا 100. به عبارت دیگر، اگر یک مشتری امتیاز 0 داشته باشد، هرگز پول خرج نمی کند و اگر امتیاز 100 باشد، بیشترین خرج را دارد.
توجه داشته باشید: می توانید مجموعه داده را دانلود کنید اینجا.
پس از دانلود مجموعه داده، خواهید دید که یک فایل CSV (مقادیر جدا شده با کاما) است به نام shopping-data.csv، ما آن را با استفاده از پاندا در یک DataFrame بارگذاری می کنیم و در آن ذخیره می کنیم customer_data متغیر:
import pandas as pd
path_to_file = '../../datasets/dbscan/dbscan-with-python-and-scikit-learn-shopping-data.csv'
customer_data = pd.read_csv(path_to_file)
برای نگاهی به پنج ردیف اول داده های ما، می توانید اجرا کنید customer_data.head():
این منجر به:
CustomerID Genre Age Annual Income (k$) Spending Score (1-100)
0 1 Male 19 15 39
1 2 Male 21 15 81
2 3 Female 20 16 6
3 4 Female 23 16 77
4 5 Female 31 17 40
با بررسی داده ها، می توانیم شماره شناسه مشتری، ژانر، سن، درآمد بر حسب k$ و امتیازات هزینه را مشاهده کنیم. به خاطر داشته باشید که برخی یا همه این متغیرها در مدل استفاده خواهند شد. مثلاً اگر قرار بود استفاده کنیم Age و Spending Score (1-100) به عنوان متغیرهای DBSCAN، که از متریک فاصله استفاده می کند، مهم است که آنها را به یک مقیاس مشترک برسانید تا از ایجاد اعوجاج جلوگیری شود. Age در سال اندازه گیری می شود و Spending Score (1-100) محدوده محدودی از 0 تا 100 دارد. این بدان معنی است که ما نوعی مقیاس بندی داده ها را انجام خواهیم داد.
همچنین میتوانیم با مشاهده سازگاری نوع دادهها و بررسی اینکه آیا مقادیر گمشدهای وجود دارد که باید با اجرای Panda درمان شوند، بررسی کنیم که آیا دادهها به پیش پردازش بیشتری به غیر از مقیاسبندی نیاز دارند یا خیر. info() روش:
customer_data.info()
این نمایش می دهد:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 200 entries, 0 to 199
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 CustomerID 200 non-null int64
1 Genre 200 non-null object
2 Age 200 non-null int64
3 Annual Income (k$) 200 non-null int64
4 Spending Score (1-100) 200 non-null int64
dtypes: int64(4), object(1)
memory usage: 7.9+ KB
ما می توانیم مشاهده کنیم که هیچ مقدار گم نشده ای وجود ندارد زیرا 200 ورودی غیر تهی برای هر ویژگی مشتری وجود دارد. همچنین میتوانیم ببینیم که فقط ستون ژانر دارای محتوای متنی است، زیرا یک متغیر طبقهبندی است که به صورت نمایش داده میشود. object، و همه ویژگی های دیگر از نوع عددی هستند int64. بنابراین، از نظر سازگاری نوع داده و عدم وجود مقادیر صفر، داده های ما برای تجزیه و تحلیل بیشتر آماده است.
میتوانیم به تجسم دادهها ادامه دهیم و مشخص کنیم که استفاده از کدام ویژگی در DBSCAN جالب است. پس از انتخاب آن ویژگی ها، می توانیم آنها را مقیاس بندی کنیم.
این مجموعه داده مشتری همان مجموعه ای است که در راهنمای قطعی ما برای خوشه بندی سلسله مراتبی استفاده شده است. برای کسب اطلاعات بیشتر در مورد این داده ها، روش کاوش آن ها و معیارهای فاصله، می توانید نگاهی به راهنمای قطعی برای خوشه بندی سلسله مراتبی با پایتون و Scikit-Learn بیندازید!
تجسم داده ها
با استفاده از Seaborn’s pairplot()، می توانیم برای هر ترکیبی از ویژگی ها یک نمودار پراکندگی رسم کنیم. از آنجا که CustomerID فقط یک شناسه است و نه یک ویژگی، ما آن را با آن حذف خواهیم کرد drop() قبل از طرح ریزی:
import seaborn as sns
customer_data = customer_data.drop('CustomerID', axis=1)
sns.pairplot(customer_data);
این خروجی:

هنگامی که به ترکیب ویژگی های تولید شده توسط pairplot، نمودار از Annual Income (k$) با Spending Score (1-100) به نظر می رسد حدود 5 گروه از نقاط را نشان می دهد. به نظر می رسد این امیدوار کننده ترین ترکیب ویژگی ها باشد. ما می توانیم لیستی با نام آنها ایجاد کنیم، آنها را از بین انتخاب کنیم customer_data DataFrame و انتخاب را در قسمت ذخیره کنید customer_data متغیر دوباره برای استفاده در مدل آینده ما.
selected_cols = ('Annual Income (k$)', 'Spending Score (1-100)')
customer_data = customer_data(selected_cols)
پس از انتخاب ستونها، میتوانیم مقیاسبندی مورد بحث در قسمت قبل را انجام دهیم. برای آوردن ویژگی ها به یک مقیاس یا استاندارد کردن آنها، ما می توانیم import Scikit-Learn’s StandardScaler، آن را ایجاد کنید، داده های ما را برای محاسبه میانگین و انحراف معیار آن برازش دهید و داده ها را با تفریق میانگین آن و تقسیم آن بر انحراف معیار تبدیل کنید. این را می توان در یک مرحله با fit_transform() روش:
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
scaled_data = ss.fit_transform(customer_data)
اکنون متغیرها مقیاسبندی شدهاند و میتوانیم آنها را با چاپ کردن محتوای آن بررسی کنیم scaled_data متغیر. از طرف دیگر، ما همچنین می توانیم آنها را به یک جدید اضافه کنیم scaled_customer_data DataFrame همراه با نام ستون و استفاده از head() روش دوباره:
scaled_customer_data = pd.DataFrame(columns=selected_cols, data=scaled_data)
scaled_customer_data.head()
این خروجی:
Annual Income (k$) Spending Score (1-100)
0 -1.738999 -0.434801
1 -1.738999 1.195704
2 -1.700830 -1.715913
3 -1.700830 1.040418
4 -1.662660 -0.395980
این داده برای خوشه بندی آماده است! هنگام معرفی DBSCAN، حداقل تعداد امتیاز و اپسیلون را ذکر کردیم. این دو مقدار باید قبل از ایجاد مدل انتخاب شوند. بیایید ببینیم چگونه انجام می شود.
انتخاب حداقل نمونه ها و اپسیلون
برای انتخاب حداقل تعداد نقاط برای خوشهبندی DBSCAN، یک قاعده کلی وجود دارد که بیان میکند که باید برابر یا بیشتر از تعداد ابعاد در دادهها به اضافه یک باشد، مانند:
$$
\text{دقیقه نقاط} >= \text{ابعاد داده} + 1
$$
ابعاد تعداد ستون ها در دیتافریم است، ما از 2 ستون استفاده می کنیم، بنابراین حداقل. امتیاز باید 2+1 باشد که 3 یا بالاتر است. برای این مثال، بیایید استفاده کنیم 5 دقیقه. نکته ها.
$$
\text{5 (حداقل امتیاز)} >= \text{2 (ابعاد داده)} + 1
$$
اکنون برای انتخاب مقدار ε روشی وجود دارد که در آن a نزدیکترین همسایه ها الگوریتم برای یافتن فواصل تعداد از پیش تعریف شده نزدیکترین نقاط برای هر نقطه استفاده می شود. این تعداد از پیش تعریف شده همسایه ها حداقل است. نقاط منهای 1 را انتخاب کرده ایم. بنابراین، در مورد ما، الگوریتم 5-1 یا 4 نزدیکترین نقطه را برای هر نقطه از داده های ما پیدا می کند. آنها هستند k-همسایه ها و ما ک برابر 4.
$$
\text{k-neighbors} = \text{min. امتیاز} – 1
$$
پس از یافتن همسایه ها، فواصل آنها را از بزرگ به کوچکتر ترتیب می دهیم و فاصله محور y و نقاط را رسم می کنیم. روی محور x با نگاهی به نمودار، متوجه خواهیم شد که کجا شبیه خمیدگی یک آرنج است و نقطه محور y که خم شدن آرنج را توصیف می کند مقدار ε پیشنهادی است.
توجه داشته باشید: این امکان وجود دارد که نمودار برای یافتن مقدار ε دارای یک یا چند “خم آرنج” باشد، بزرگ یا کوچک، وقتی این اتفاق افتاد، می توانید مقادیر را پیدا کنید، آنها را آزمایش کنید و آنهایی را انتخاب کنید که نتایجی را دارند که بهترین خوشه ها را توصیف می کنند. یا با مشاهده معیارهای نمودارها.
برای انجام این مراحل می توانیم import الگوریتم را با داده ها برازش می دهیم و سپس می توانیم فواصل و شاخص های هر نقطه را با kneighbors() روش:
from sklearn.neighbors import NearestNeighbors
import numpy as np
nn = NearestNeighbors(n_neighbors=4)
nbrs = nn.fit(scaled_customer_data)
distances, indices = nbrs.kneighbors(scaled_customer_data)
پس از یافتن فاصله ها، می توانیم آنها را از بزرگترین به کوچکترین مرتب کنیم. از آنجایی که ستون اول آرایه فاصله از نقطه به خودش است (یعنی همه 0 هستند) و ستون دوم کوچکترین فواصل را شامل می شود و به دنبال آن ستون سوم که فواصل بیشتری نسبت به دومی دارد و بنابراین روی، می توانیم فقط مقادیر ستون دوم را انتخاب کرده و در آن ذخیره کنیم distances متغیر:
distances = np.sort(distances, axis=0)
distances = distances(:,1)
اکنون که کوچکترین فاصله های خود را مرتب کرده ایم، می توانیم import matplotlibفاصله ها را رسم کرده و یک خط قرمز بکشید روی جایی که “خم آرنج” است:
import matplotlib.pyplot as plt
plt.figure(figsize=(6,3))
plt.plot(distances)
plt.axhline(y=0.24, color='r', linestyle='--', alpha=0.4)
plt.title('Kneighbors distance graph')
plt.xlabel('Data points')
plt.ylabel('Epsilon value')
plt.show();
این هم نتیجه:

توجه داشته باشید که هنگام رسم خط، مقدار ε را دریابیم، در این مورد، این است 0.24.
ما در نهایت حداقل امتیاز و ε را داریم. با هر دو متغیر می توانیم مدل DBSCAN را ایجاد و اجرا کنیم.
ایجاد یک مدل DBSCAN
برای ایجاد مدل، ما می توانیم import آن را از Scikit-Learn، با ε ایجاد کنید که همان است eps آرگومان، و حداقل نقاطی که به آن اشاره می شود mean_samples بحث و جدل. سپس می توانیم آن را در یک متغیر ذخیره کنیم، بیایید آن را فراخوانی کنیم dbs و آن را با داده های مقیاس بندی شده مطابقت دهید:
from sklearn.cluster import DBSCAN
dbs = DBSCAN(eps=0.24, min_samples=5)
dbs.fit(scaled_customer_data)
دقیقاً مانند آن، مدل DBSCAN ما ایجاد و آموزش داده شده است روی داده! برای استخراج نتایج، ما به labels_ ویژگی. ما همچنین می توانیم یک جدید ایجاد کنیم labels ستون در scaled_customer_data چارچوب داده و آن را با برچسب های پیش بینی شده پر کنید:
labels = dbs.labels_
scaled_customer_data('labels') = labels
scaled_customer_data.head()
این هم نتیجه نهایی:
Annual Income (k$) Spending Score (1-100) labels
0 -1.738999 -0.434801 -1
1 -1.738999 1.195704 0
2 -1.700830 -1.715913 -1
3 -1.700830 1.040418 0
4 -1.662660 -0.395980 -1
توجه داشته باشید که ما برچسب هایی با -1 ارزش های؛ اینها هستند نقاط نویز، آنهایی که به هیچ خوشه ای تعلق ندارند. برای اینکه بدانیم الگوریتم چند نقطه نویز پیدا کرده است، میتوانیم شمارش کنیم که مقدار -1 چند بار در لیست برچسبهای ما ظاهر میشود:
labels_list = list(scaled_customer_data('labels'))
n_noise = labels_list.count(-1)
print("Number of noise points:", n_noise)
این خروجی:
Number of noise points: 62
ما قبلاً می دانیم که 62 نقطه از داده های اصلی ما از 200 نقطه نویز در نظر گرفته شده است. این نویز زیادی است، که نشان میدهد شاید خوشهبندی DBSCAN بسیاری از نقاط را به عنوان بخشی از یک خوشه در نظر نگرفته است. وقتی داده ها را ترسیم کنیم، به زودی متوجه خواهیم شد که چه اتفاقی افتاده است.
در ابتدا، زمانی که داده ها را مشاهده کردیم، به نظر می رسید که دارای 5 خوشه نقطه است. برای اینکه بدانیم DBSCAN چند خوشه تشکیل داده است، می توانیم تعداد برچسب هایی را که 1- نیستند بشماریم. راه های زیادی برای نوشتن آن کد وجود دارد. در اینجا، ما یک حلقه for نوشتهایم که برای دادههایی که DBSCAN در آنها خوشههای زیادی پیدا کرده است نیز کار میکند:
total_labels = np.unique(labels)
n_labels = 0
for n in total_labels:
if n != -1:
n_labels += 1
print("Number of clusters:", n_labels)
این خروجی:
Number of clusters: 6
میتوانیم ببینیم که الگوریتم دادهها را 6 خوشه، با نقاط نویز زیاد پیشبینی میکرد. بیایید آن را با ترسیم نقشه Seaborn تجسم کنیم scatterplot:
sns.scatterplot(data=scaled_customer_data,
x='Annual Income (k$)', y='Spending Score (1-100)',
hue='labels', palette='muted').set_title('DBSCAN found clusters');
این منجر به:

با نگاهی به نمودار، میتوانیم ببینیم که DBSCAN نقاطی را که بهطور متراکمتری به هم متصل شدهاند، گرفته است، و نقاطی که میتوان آنها را بخشی از همان خوشه در نظر گرفت، نویز بودند یا در نظر گرفته میشد که خوشه کوچکتر دیگری را تشکیل دهند.

اگر خوشه ها را برجسته کنیم، توجه کنید که چگونه DBSCAN خوشه 1 را به طور کامل دریافت می کند، که خوشه ای با فضای کمتر بین نقاط است. سپس بخشهایی از خوشههای 0 و 3 را دریافت میکند که نقاط نزدیک به هم هستند و نقاط فاصله بیشتری را به عنوان نویز در نظر میگیرند. همچنین نقاط نیمه سمت چپ پایین را به عنوان نویز در نظر می گیرد و نقاط پایین سمت راست را به 3 خوشه تقسیم می کند و یک بار دیگر خوشه های 4، 2 و 5 را در جایی که نقاط به هم نزدیکتر هستند، می گیرد.
میتوانیم به این نتیجه برسیم که DBSCAN برای گرفتن نواحی متراکم خوشهها عالی بود، اما نه برای شناسایی طرح بزرگتر دادهها، یعنی حدود 5 خوشه. آزمایش الگوریتم های خوشه بندی بیشتر با داده هایمان جالب خواهد بود. بیایید ببینیم که آیا یک متریک این فرضیه را تأیید می کند یا خیر.
ارزیابی الگوریتم
برای ارزیابی DBSCAN ما از نمره سیلوئت که فاصله بین نقاط یک خوشه و فاصله بین خوشه ها را در نظر می گیرد.
توجه داشته باشید: در حال حاضر، اکثر معیارهای خوشه بندی واقعاً برای ارزیابی DBSCAN مناسب نیستند زیرا مبتنی بر آنها نیستند. روی تراکم در اینجا، ما از امتیاز silhouette استفاده می کنیم زیرا قبلاً در Scikit-learn پیاده سازی شده است و سعی می کند به شکل خوشه نگاه کند.
برای داشتن یک ارزیابی مناسب تر، می توانید از آن استفاده کنید یا با آن ترکیب کنید اعتبارسنجی خوشهبندی مبتنی بر چگالی متریک (DBCV) که به طور خاص برای خوشه بندی مبتنی بر چگالی طراحی شده است. یک پیاده سازی برای DBCV موجود است روی این GitHub.
اول، ما می توانیم import silhouette_score از Scikit-Learn، سپس، ستون ها و برچسب های ما را به آن منتقل کنید:
from sklearn.metrics import silhouette_score
s_score = silhouette_score(scaled_customer_data, labels)
print(f"Silhouette coefficient: {s_score:.3f}")
این خروجی:
Silhouette coefficient: 0.506
با توجه به این امتیاز، به نظر می رسد DBSCAN می تواند تقریباً 50 درصد از داده ها را ضبط کند.
نتیجه
مزایا و معایب DBSCAN
DBSCAN یک الگوریتم یا مدل خوشه بندی بسیار منحصر به فرد است.
اگر به مزایای آن نگاه کنیم، در برداشتن مناطق متراکم در داده ها و نقاط دور از دیگران بسیار خوب است. این بدان معنی است که داده ها نباید شکل خاصی داشته باشند و می توانند توسط نقاط دیگری احاطه شوند، البته تا زمانی که آنها نیز به طور متراکم به هم متصل باشند.
از ما می خواهد که حداقل نقاط و ε را مشخص کنیم، اما نیازی به تعیین تعداد خوشه ها از قبل، مانند K-Means نیست. همچنین می تواند با پایگاه داده های بسیار بزرگ استفاده شود زیرا برای داده های با ابعاد بالا طراحی شده است.
در مورد معایب آن، دیدهایم که نمیتواند چگالیهای مختلف را در یک خوشه ثبت کند، بنابراین با تفاوتهای بزرگ در چگالی کار سختی دارد. وابسته هم هست روی متریک فاصله و مقیاس بندی نقاط. این به این معنی است که اگر داده ها به خوبی درک نشده باشند، با تفاوت در مقیاس و با متریک فاصله ای که منطقی نیست، احتمالاً در درک آن شکست خواهد خورد.
برنامه های افزودنی DBSCAN
الگوریتم های دیگری مانند DBSCAN سلسله مراتبی (HDBSCAN) و نقاط ترتیب برای شناسایی ساختار خوشه بندی (OPTICS)، که پسوند DBSCAN محسوب می شوند.
هر دو HDBSCAN و OPTICS معمولاً زمانی که خوشههایی با چگالیهای متفاوت در دادهها وجود دارند بهتر عمل میکنند و همچنین نسبت به انتخاب یا حداقل اولیه حساسیت کمتری دارند. نقاط و پارامترهای ε.
(برچسبها به ترجمه)# python
منتشر شده در 1403-01-01 10:24:02



