سرور مجازی NVMe

Minimax با هرس آلفا-بتا در پایتون

Pythonبرنامه نویسیهوش مصنوعی (AI)

توسط مهران در دی ۳۰, ۱۴۰۲

سرفصلهای مطلب

زمان لازم برای مطالعه: 13 دقیقه

معرفی

بسیار در اواخر دهه 1920 جان فون نویمان مشکل اصلی در تئوری بازی‌ها را که تا به امروز مطرح است، ایجاد کرد:

بازیکنان اس₁، س₂، …، س_n در حال انجام یک بازی G. بازیکن باید کدام حرکت را انجام دهد_متر برای رسیدن به بهترین نتیجه ممکن بازی کنید؟

اندکی پس از آن، مشکلاتی از این دست به چالشی با اهمیت برای توسعه یکی از محبوب ترین زمینه های امروزی در علوم کامپیوتر – هوش مصنوعی تبدیل شدند. برخی از بزرگترین دستاوردها در هوش مصنوعی به دست آمده است روی موضوع بازی های استراتژیک – قهرمانان جهان در بازی های استراتژیک مختلف قبلاً توسط رایانه ها شکست خورده اند، به عنوان مثال در شطرنج، چکرز، تخته نرد، و اخیراً (2016) حتی Go.

اگرچه این برنامه ها بسیار موفق هستند، اما روش تصمیم گیری آنها با انسان ها بسیار متفاوت است. اکثر این برنامه ها مبتنی هستند روی الگوریتم های جستجوی کارآمد، و از این اواخر روی همچنین یادگیری ماشینی

را الگوریتم Minimax یک الگوریتم نسبتا ساده است که برای تصمیم گیری بهینه در نظریه بازی ها و هوش مصنوعی استفاده می شود. باز هم، از آنجایی که این الگوریتم ها به شدت متکی هستند روی با کارآمد بودن، عملکرد الگوریتم وانیل را می توان با استفاده از هرس آلفا-بتا به شدت بهبود بخشید – در این مقاله به هر دو خواهیم پرداخت.

اگرچه ما هر بازی را به صورت جداگانه تجزیه و تحلیل نمی کنیم، اما به طور خلاصه برخی از مفاهیم کلی را که برای دو نفره مرتبط هستند توضیح خواهیم داد. غیر تعاونی حاصل جمع صفر متقارن بازی با اطلاعات کامل – شطرنج، برو، تیک تاک، تخته نرد، ریورسی، چکرز، مانکالا، 4 در یک ردیف و غیره …

همانطور که احتمالا متوجه شدید، هیچ یک از این بازی‌ها بازی‌هایی نیستند که به عنوان مثال، بازیکن نداند کارت‌های حریف دارد، یا جایی که بازیکن باید اطلاعات خاصی را حدس بزند.

تعریف اصطلاحات

قوانین بسیاری از این بازی ها توسط موقعیت های قانونی (یا کشورهای قانونی) و حرکات قانونی برای هر موقعیت قانونی برای هر موقعیت حقوقی می توان به طور موثر تمام حرکت های قانونی را تعیین کرد. برخی از مواضع حقوقی هستند موقعیت های شروع و برخی هستند موقعیت های پایانی.

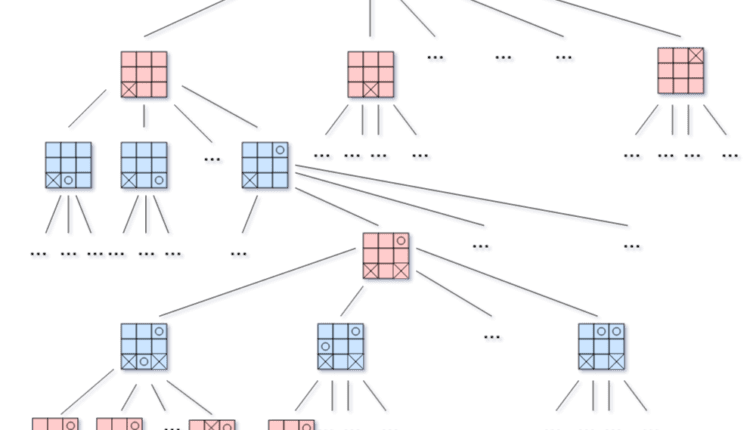
بهترین راه برای توصیف این اصطلاحات استفاده از یک نمودار درختی است که گره‌های آن موقعیت‌های قانونی و یال‌های آن حرکات قانونی هستند. نمودار هدایت شده است زیرا لزوماً به این معنی نیست که ما دقیقاً می توانیم به همان جایی که در حرکت قبلی آمده ایم برگردیم، مثلاً در شطرنج یک پیاده فقط می تواند به جلو برود. این نمودار a نامیده می شود درخت بازی. حرکت به سمت پایین درخت بازی نشان دهنده حرکت یکی از بازیکنان است و وضعیت بازی از یک موقعیت قانونی به موقعیت دیگر تغییر می کند.

در اینجا یک تصویر از یک درخت بازی برای یک بازی تیک تاک است:

شبکه های آبی رنگ نوبت بازیکن X و شبکه های قرمز رنگ نوبت بازیکن O هستند. موقعیت پایانی (برگ درخت) هر شبکه ای است که در آن یکی از بازیکنان برنده شود یا تخته پر باشد و هیچ برنده ای وجود نداشته باشد.

را درخت بازی کامل درخت بازی است که root موقعیت شروع است و تمام برگ ها موقعیت های پایانی هستند. هر درخت بازی کامل به همان تعداد گره دارد که بازی نتایج ممکن برای هر حرکت قانونی انجام شده دارد. به راحتی می توان متوجه شد که حتی برای بازی های کوچک مانند tic-tac-toe درخت کامل بازی بزرگ است. به همین دلیل، ایجاد صریح یک درخت بازی کامل به عنوان ساختار در حین نوشتن برنامه ای که قرار است بهترین حرکت را در هر لحظه پیش بینی کند، تمرین خوبی نیست. با این حال، گره ها باید به طور ضمنی در ایجاد شوند process از بازدید

تعریف می کنیم پیچیدگی حالت-فضای یک بازی به عنوان تعدادی از موقعیت های بازی قانونی قابل دسترسی از موقعیت شروع بازی، و عامل انشعاب به تعداد فرزندان در هر کدام node (اگر این عدد ثابت نیست، استفاده از میانگین معمول است).

برای tic-tac-toe، حد بالایی برای اندازه فضای حالت 3 است⁹=19683. این عدد را برای بازی هایی مانند شطرنج تصور کنید! از این رو، جستجو در کل درخت برای یافتن بهترین حرکت ما در هر زمان که به نوبت انجام می دهیم، بسیار ناکارآمد و کند خواهد بود.

به همین دلیل است که Minimax در تئوری بازی ها از اهمیت بالایی برخوردار است.

تئوری پشت مینیمکس

الگوریتم Minimax متکی است روی جستجوی سیستماتیک، یا به طور دقیق تر گفته می شود – روی نیروی بی رحم و یک تابع ارزیابی ساده. بیایید فرض کنیم که هر بار در طول تصمیم گیری برای حرکت بعدی، یک درخت کامل را جستجو می کنیم، تا برگ ها. ما به طور موثر تمام نتایج ممکن را بررسی می کنیم و هر بار که می توانیم بهترین حرکت ممکن را تعیین کنیم.

با این حال، برای بازی های غیر پیش پا افتاده، این عمل غیر قابل اجرا است. حتی جستجو در عمق معین گاهی اوقات زمان غیر قابل قبولی را می طلبد. بنابراین، Minimax جستجو را در عمق درخت نسبتاً کم با کمک مناسب اعمال می کند اکتشافی، و به خوبی طراحی شده و در عین حال ساده است عملکرد ارزیابی.

با این رویکرد ما اطمینان خود را در یافتن بهترین حرکت ممکن از دست می دهیم، اما در اکثر موارد تصمیمی که مینی مکس می گیرد بسیار بهتر از تصمیم هر انسانی است.

حالا بیایید نگاهی دقیق‌تر به عملکرد ارزیابی که قبلاً ذکر کردیم بیاندازیم. برای تعیین یک حرکت خوب (نه لزوما بهترین) برای یک بازیکن خاص، باید به نحوی گره ها (موقعیت ها) را ارزیابی کنیم تا بتوانیم یکی را از نظر کیفیت با دیگری مقایسه کنیم.

تابع ارزیابی یک عدد ثابت است که مطابق با ویژگی های خود بازی، به هر کدام اختصاص داده می شود node (موقعیت).

ذکر این نکته ضروری است که عملکرد ارزیابی نباید متکی باشد روی جستجوی گره های قبلی و نه موارد زیر. باید به سادگی وضعیت بازی و شرایطی را که هر دو بازیکن در آن قرار دارند تجزیه و تحلیل کند.

لازم است که تابع ارزیابی تا حد امکان حاوی اطلاعات مرتبط باشد، اما روی از سوی دیگر – از آنجایی که در حال محاسبه است زیاد بار – باید ساده باشد.

معمولاً مجموعه تمام موقعیت‌های ممکن را در بخش متقارن ترسیم می‌کند:

$$
\mathcal{F} : \mathcal{P} \rightarrow (-M, M)
$$

ارزش M فقط به برگهایی اختصاص داده می شود که برنده اولین بازیکن است و ارزش دارد -M به جایی که برنده بازیکن دوم است ترک کند.

در بازی‌های حاصل جمع صفر، مقدار تابع ارزیابی معنای مخالف دارد – آنچه برای بازیکن اول بهتر است برای بازیکن دوم بدتر است و بالعکس. از این رو، مقدار موقعیت های متقارن (اگر بازیکنان نقش ها را تغییر دهند) باید فقط با علامت متفاوت باشد.

یک روش معمول این است که ارزیابی‌های برگ‌ها را با کم کردن عمق دقیقاً آن برگ تغییر می‌دهند، به طوری که از بین تمام حرکاتی که منجر به پیروزی می‌شود، الگوریتم بتواند حرکتی را انتخاب کند که این کار را در کمترین تعداد مراحل انجام می‌دهد (یا حرکتی را که به تعویق می‌افتد انتخاب کند. ضرر اگر اجتناب ناپذیر باشد).

در اینجا یک تصویر ساده از مراحل Minimax آورده شده است. ما در این مورد به دنبال حداقل مقدار هستیم.

لایه سبز رنگ را فرا می خواند Max() روش روی گره ها در گره های فرزند و لایه قرمز رنگ را فرا می خواند Min() روش روی گره های کودک

ارزیابی برگها:

تصمیم گیری بهترین حرکت برای بازیکن سبز با استفاده از عمق 3:

ایده این است که بهترین حرکت ممکن را برای یک معین پیدا کنید node، عمق و عملکرد ارزیابی.

در این مثال فرض کرده ایم که بازیکن سبز به دنبال مقادیر مثبت است، در حالی که بازیکن صورتی به دنبال ارزش های منفی است. الگوریتم در درجه اول فقط گره ها را در عمق داده شده ارزیابی می کند و بقیه مراحل بازگشتی. مقادیر بقیه گره ها حداکثر مقادیر فرزندان مربوطه آنهاست اگر نوبت بازیکن سبز باشد، یا به طور مشابه، حداقل مقدار اگر نوبت بازیکن صورتی باشد. ارزش در هر کدام node بهترین حرکت بعدی را با در نظر گرفتن اطلاعات داده شده نشان می دهد.

هنگام جستجوی درخت بازی، فقط گره ها را بررسی می کنیم روی یک عمق ثابت (داده شده)، نه قبل و نه بعد. این پدیده اغلب نامیده می شود اثر افق.

باز کردن کتاب ها و تیک تاک

در بازی های استراتژیک، به جای اینکه اجازه دهید برنامه جستجو را شروع کند process در همان ابتدای بازی، استفاده از باز کردن کتاب ها – لیستی از حرکات شناخته شده و سازنده که مکرر و سازنده شناخته می شوند در حالی که اگر به تابلو نگاه کنیم هنوز اطلاعات زیادی در مورد وضعیت خود بازی نداریم.

در ابتدا، بازی خیلی زود است و تعداد موقعیت‌های بالقوه آنقدر زیاد است که نمی‌توان به طور خودکار تصمیم گرفت که کدام حرکت مطمئناً به وضعیت بازی بهتر (یا برنده شدن) منجر می‌شود.

با این حال، الگوریتم حرکت‌های بالقوه بعدی را در هر نوبت دوباره ارزیابی می‌کند و همیشه مسیری را انتخاب می‌کند که در آن لحظه به نظر می‌رسد سریع‌ترین مسیر برای پیروزی باشد. بنابراین، اقداماتی را که برای تکمیل آنها بیش از یک حرکت طول می‌کشد، اجرا نمی‌کند، و به همین دلیل قادر به انجام برخی «ترفندهای» شناخته‌شده نیست. اگر هوش مصنوعی علیه یک انسان بازی کند، به احتمال زیاد انسان ها فوراً قادر به جلوگیری از این امر خواهند بود.

اگر، روی از سوی دیگر، نگاهی به شطرنج بیندازیم، به سرعت متوجه غیرعملی بودن حل شطرنج با اجبار بی رحمانه در درخت بازی خواهیم شد. برای نشان دادن این، کلود شانون حد پایین پیچیدگی درخت بازی شطرنج را محاسبه کرد و در نتیجه حدود 10¹²⁰ بازی های ممکن.

این عدد چقدر است؟ برای مرجع، اگر جرم یک الکترون را مقایسه کنیم (10^-30کیلوگرم) به جرم کل جهان شناخته شده (10⁵⁰-10⁶⁰کیلوگرم)، نسبت به ترتیب 10 خواهد بود⁸⁰-10⁹⁰.

این ~0.00000000000000000000000000000000000000000000000000000000000000000000000000000001٪ از عدد شانون است.

تصور کنید که یک الگوریتم را برای انجام وظیفه تعیین کنید تک تک از آن ترکیبات فقط برای گرفتن یک تصمیم واحد. عملا غیر ممکن است.

حتی پس از 10 حرکت، تعداد بازی های ممکن بسیار زیاد است:

تعداد حرکات	تعداد بازی های ممکن
1	20
2	40
3	8902
4	197281
5	4,865,609
6	119,060,324
7	3,195,901,860
8	84,998,978,956
9	2,439,530,234,167
10	69,352,859,712,417

بیایید این مثال را به یک بازی تیک تاک ببریم. همانطور که احتمالا می دانید، معروف ترین استراتژی بازیکن X شروع در هر یک از گوشه ها است که به بازیکن O بیشترین فرصت برای اشتباه را می دهد. اگر بازیکن O به غیر از مرکز بازی کند و X استراتژی اولیه خود را ادامه دهد، این یک برد تضمینی برای X است. کتاب های افتتاحیه دقیقاً این هستند – چند راه خوب برای فریب دادن حریف در همان ابتدا برای به دست آوردن مزیت، یا در بهترین حالت، یک برد.

برای ساده‌سازی کد و رسیدن به هسته‌ی الگوریتم، در مثال فصل بعد، ما از کتاب‌های باز کردن یا هیچ ترفندی استفاده نمی‌کنیم. ما از همان ابتدا اجازه جستجوی مینیمکس را خواهیم داد، بنابراین تعجب نکنید که الگوریتم هرگز استراتژی گوشه را توصیه نمی کند.

پیاده سازی Minimax در پایتون

در کد زیر، ما از یک تابع ارزیابی استفاده خواهیم کرد که نسبتاً ساده و رایج برای همه بازی‌هایی است که در آن‌ها امکان جستجوی کل درخت، تا برگ‌ها وجود دارد.

دارای 3 مقدار ممکن است:

-1 اگر بازیکنی که به دنبال حداقل برنده است
0 اگر مساوی باشد
1 اگر بازیکنی که به دنبال حداکثر برنده است

از آنجایی که ما این را از طریق یک بازی tic-tac-toe پیاده سازی خواهیم کرد، بیایید بلوک های سازنده را مرور کنیم. ابتدا بیایید یک سازنده بسازیم و تابلو را ترسیم کنیم:





import time

class Game:
    def __init__(self):
        self.initialize_game()

    def initialize_game(self):
        self.current_state = (('.','.','.'),
                              ('.','.','.'),
                              ('.','.','.'))

        
        self.player_turn = 'X'

    def draw_board(self):
        for i in range(0, 3):
            for j in range(0, 3):
                print('{}|'.format(self.current_state(i)(j)), end=" ")
            print()
        print()

همه روش های رسیدگی به جز روش اصلی متعلق به Game کلاس

ما صحبت کرده ایم حرکات قانونی در بخش های ابتدایی مقاله برای اطمینان از اینکه قوانین را رعایت می کنیم، به راهی برای بررسی قانونی بودن یک حرکت نیاز داریم:


def is_valid(self, px, py):
    if px < 0 or px > 2 or py < 0 or py > 2:
        return False
    elif self.current_state(px)(py) != '.':
        return False
    else:
        return True

سپس، ما به یک راه ساده برای بررسی اینکه آیا بازی به پایان رسیده است نیاز داریم. در تیک تاک، بازیکن می تواند با اتصال سه علامت متوالی در یک خط افقی، مورب یا عمودی برنده شود:


def is_end(self):
    
    for i in range(0, 3):
        if (self.current_state(0)(i) != '.' and
            self.current_state(0)(i) == self.current_state(1)(i) and
            self.current_state(1)(i) == self.current_state(2)(i)):
            return self.current_state(0)(i)

    
    for i in range(0, 3):
        if (self.current_state(i) == ('X', 'X', 'X')):
            return 'X'
        elif (self.current_state(i) == ('O', 'O', 'O')):
            return 'O'

    
    if (self.current_state(0)(0) != '.' and
        self.current_state(0)(0) == self.current_state(1)(1) and
        self.current_state(0)(0) == self.current_state(2)(2)):
        return self.current_state(0)(0)

    
    if (self.current_state(0)(2) != '.' and
        self.current_state(0)(2) == self.current_state(1)(1) and
        self.current_state(0)(2) == self.current_state(2)(0)):
        return self.current_state(0)(2)

    
    for i in range(0, 3):
        for j in range(0, 3):
            
            if (self.current_state(i)(j) == '.'):
                return None

    
    return '.'

هوش مصنوعی که ما در برابر آن بازی می کنیم به دنبال دو چیز است – به حداکثر رساندن امتیاز خود و به حداقل رساندن امتیاز ما. برای انجام این کار، ما یک max() روشی که هوش مصنوعی برای تصمیم گیری بهینه استفاده می کند.


def max(self):

    
    
    
    

    
    maxv = -2

    px = None
    py = None

    result = self.is_end()

    
    
    
    
    
    if result == 'X':
        return (-1, 0, 0)
    elif result == 'O':
        return (1, 0, 0)
    elif result == '.':
        return (0, 0, 0)

    for i in range(0, 3):
        for j in range(0, 3):
            if self.current_state(i)(j) == '.':
                
                
                self.current_state(i)(j) = 'O'
                (m, min_i, min_j) = self.min()
                
                if m > maxv:
                    maxv = m
                    px = i
                    py = j
                
                self.current_state(i)(j) = '.'
    return (maxv, px, py)

با این حال، ما همچنین شامل یک min() روشی که به ما کمک می کند تا امتیاز هوش مصنوعی را به حداقل برسانیم:


def min(self):

    
    
    
    

    
    minv = 2

    qx = None
    qy = None

    result = self.is_end()

    if result == 'X':
        return (-1, 0, 0)
    elif result == 'O':
        return (1, 0, 0)
    elif result == '.':
        return (0, 0, 0)

    for i in range(0, 3):
        for j in range(0, 3):
            if self.current_state(i)(j) == '.':
                self.current_state(i)(j) = 'X'
                (m, max_i, max_j) = self.max()
                if m < minv:
                    minv = m
                    qx = i
                    qy = j
                self.current_state(i)(j) = '.'

    return (minv, qx, qy)

و در نهایت، بیایید یک حلقه بازی ایجاد کنیم که به ما امکان می دهد در برابر هوش مصنوعی بازی کنیم:

def play(self):
    while True:
        self.draw_board()
        self.result = self.is_end()

        
        if self.result != None:
            if self.result == 'X':
                print('The winner is X!')
            elif self.result == 'O':
                print('The winner is O!')
            elif self.result == '.':
                print("It's a tie!")

            self.initialize_game()
            return

        
        if self.player_turn == 'X':

            while True:

                start = time.time()
                (m, qx, qy) = self.min()
                end = time.time()
                print('Evaluation time: {}s'.format(round(end - start, 7)))
                print('Recommended move: X = {}, Y = {}'.format(qx, qy))

                px = int(input('Insert the X coordinate: '))
                py = int(input('Insert the Y coordinate: '))

                (qx, qy) = (px, py)

                if self.is_valid(px, py):
                    self.current_state(px)(py) = 'X'
                    self.player_turn = 'O'
                    break
                else:
                    print('The move is not valid! Try again.')

        
        else:
            (m, px, py) = self.max()
            self.current_state(px)(py) = 'O'
            self.player_turn = 'X'

بیایید بازی را شروع کنیم!

def main():
    g = Game()
    g.play()

if __name__ == "__main__":
    main()

اکنون نگاهی می اندازیم به این که وقتی دنباله چرخش های توصیه شده را دنبال کنیم چه اتفاقی می افتد – یعنی بهینه بازی کنیم:

.| .| .|
.| .| .|
.| .| .|

Evaluation time: 5.0726919s
Recommended move: X = 0, Y = 0
Insert the X coordinate: 0
Insert the Y coordinate: 0
X| .| .|
.| .| .|
.| .| .|

X| .| .|
.| O| .|
.| .| .|

Evaluation time: 0.06496s
Recommended move: X = 0, Y = 1
Insert the X coordinate: 0
Insert the Y coordinate: 1
X| X| .|
.| O| .|
.| .| .|

X| X| O|
.| O| .|
.| .| .|

Evaluation time: 0.0020001s
Recommended move: X = 2, Y = 0
Insert the X coordinate: 2
Insert the Y coordinate: 0
X| X| O|
.| O| .|
X| .| .|

X| X| O|
O| O| .|
X| .| .|

Evaluation time: 0.0s
Recommended move: X = 1, Y = 2
Insert the X coordinate: 1
Insert the Y coordinate: 2
X| X| O|
O| O| X|
X| .| .|

X| X| O|
O| O| X|
X| O| .|

Evaluation time: 0.0s
Recommended move: X = 2, Y = 2
Insert the X coordinate: 2
Insert the Y coordinate: 2
X| X| O|
O| O| X|
X| O| X|

It's a tie!

همانطور که متوجه شدید، پیروزی در برابر این نوع هوش مصنوعی غیرممکن است. اگر فرض کنیم که هم بازیکن و هم هوش مصنوعی به خوبی بازی می کنند، بازی همیشه مساوی خواهد بود. از آنجایی که هوش مصنوعی همیشه بهینه بازی می کند، اگر لغزش کنیم، بازنده خواهیم بود.

به زمان ارزیابی دقت کنید، زیرا در مثال بعدی آن را با نسخه بهبود یافته بعدی الگوریتم مقایسه خواهیم کرد.

هرس آلفا بتا

آلفا–بتا (𝛼−𝛽) الگوریتم به طور مستقل توسط چند محقق در اواسط دهه 1900 کشف شد. آلفا-بتا در واقع یک مینیمکس بهبود یافته با استفاده از یک اکتشافی است. وقتی مطمئن شود که حرکتی بدتر از حرکتی است که قبلاً مورد بررسی قرار گرفته است، ارزیابی آن را متوقف می کند. چنین حرکاتی نیازی به ارزیابی بیشتر ندارد.

هنگامی که به یک الگوریتم ساده مینی‌مکس اضافه می‌شود، همان خروجی را می‌دهد، اما شاخه‌های خاصی را که احتمالاً نمی‌تواند بر تصمیم نهایی تأثیر بگذارد، قطع می‌کند – عملکرد را به طور چشمگیری بهبود می‌بخشد.

مفهوم اصلی حفظ دو مقدار از طریق کل جستجو است:

آلفا: بهترین گزینه قبلاً بررسی شده برای بازیکن Max
بتا: بهترین گزینه قبلاً بررسی شده برای بازیکن Min

در ابتدا، آلفا بی نهایت منفی و بتا بی نهایت مثبت است، یعنی در کد ما از بدترین امتیاز ممکن برای هر دو بازیکن استفاده خواهیم کرد.

بیایید ببینیم اگر روش آلفا-بتا را اعمال کنیم، درخت قبلی چگونه به نظر می رسد:

هنگامی که جستجو به اولین منطقه خاکستری (8) می رسد، بهترین گزینه فعلی (با حداقل مقدار) را که قبلاً در مسیر کاوش شده است را برای کمینه کننده بررسی می کند که در آن لحظه 7 است. از آنجایی که 8 بزرگتر از 7 است، ما اجازه دارند تمام فرزندان بعدی را قطع کنند node ما در حال هستیم (در این مورد هیچ کدام وجود ندارد)، زیرا اگر آن حرکت را انجام دهیم، حریف حرکتی با ارزش 8 را انجام می دهد که برای ما بدتر از هر حرکت ممکنی است که حریف می توانست انجام دهد اگر ما انجام می دادیم. یک حرکت دیگر

مثال بهتر ممکن است زمانی باشد که نوبت به رنگ خاکستری بعدی می رسد. به گره هایی با مقدار -9 توجه کنید. در آن نقطه، بهترین (با حداکثر مقدار) گزینه کاوش شده در طول مسیر برای ماکزیمایزر -4 است. از آنجایی که -9 کمتر از -4 است، می‌توانیم تمام فرزندان دیگر را قطع کنیم node ما در

این روش به ما این امکان را می‌دهد که بسیاری از شاخه‌ها را نادیده بگیریم که به ارزش‌هایی منتهی می‌شوند که هیچ کمکی به تصمیم ما نمی‌کنند و به هیچ وجه بر آن تأثیر نمی‌گذارند.

با در نظر گرفتن آن، بیایید آن را اصلاح کنیم min() و max() روش های قبلی:

def max_alpha_beta(self, alpha, beta):
        maxv = -2
        px = None
        py = None

        result = self.is_end()

        if result == 'X':
            return (-1, 0, 0)
        elif result == 'O':
            return (1, 0, 0)
        elif result == '.':
            return (0, 0, 0)

        for i in range(0, 3):
            for j in range(0, 3):
                if self.current_state(i)(j) == '.':
                    self.current_state(i)(j) = 'O'
                    (m, min_i, in_j) = self.min_alpha_beta(alpha, beta)
                    if m > maxv:
                        maxv = m
                        px = i
                        py = j
                    self.current_state(i)(j) = '.'

                    
                    if maxv >= beta:
                        return (maxv, px, py)

                    if maxv > alpha:
                        alpha = maxv

        return (maxv, px, py)

 def min_alpha_beta(self, alpha, beta):

        minv = 2

        qx = None
        qy = None

        result = self.is_end()

        if result == 'X':
            return (-1, 0, 0)
        elif result == 'O':
            return (1, 0, 0)
        elif result == '.':
            return (0, 0, 0)

        for i in range(0, 3):
            for j in range(0, 3):
                if self.current_state(i)(j) == '.':
                    self.current_state(i)(j) = 'X'
                    (m, max_i, max_j) = self.max_alpha_beta(alpha, beta)
                    if m < minv:
                        minv = m
                        qx = i
                        qy = j
                    self.current_state(i)(j) = '.'

                    if minv <= alpha:
                        return (minv, qx, qy)

                    if minv < beta:
                        beta = minv

        return (minv, qx, qy)

و حالا، حلقه بازی:

  def play_alpha_beta(self):
     while True:
        self.draw_board()
        self.result = self.is_end()

        if self.result != None:
            if self.result == 'X':
                print('The winner is X!')
            elif self.result == 'O':
                print('The winner is O!')
            elif self.result == '.':
                print("It's a tie!")


            self.initialize_game()
            return

        if self.player_turn == 'X':

            while True:
                start = time.time()
                (m, qx, qy) = self.min_alpha_beta(-2, 2)
                end = time.time()
                print('Evaluation time: {}s'.format(round(end - start, 7)))
                print('Recommended move: X = {}, Y = {}'.format(qx, qy))

                px = int(input('Insert the X coordinate: '))
                py = int(input('Insert the Y coordinate: '))

                qx = px
                qy = py

                if self.is_valid(px, py):
                    self.current_state(px)(py) = 'X'
                    self.player_turn = 'O'
                    break
                else:
                    print('The move is not valid! Try again.')

        else:
            (m, px, py) = self.max_alpha_beta(-2, 2)
            self.current_state(px)(py) = 'O'
            self.player_turn = 'X'

انجام بازی مانند قبل است، اگرچه اگر نگاهی به زمان لازم برای یافتن راه حل های بهینه توسط هوش مصنوعی بیندازیم، یک تفاوت بزرگ وجود دارد:

.| .| .|
.| .| .|
.| .| .|

Evaluation time: 0.1688969s
Recommended move: X = 0, Y = 0


Evaluation time: 0.0069957s
Recommended move: X = 0, Y = 1


Evaluation time: 0.0009975s
Recommended move: X = 2, Y = 0


Evaluation time: 0.0s
Recommended move: X = 1, Y = 2


Evaluation time: 0.0s
Recommended move: X = 2, Y = 2

It's a tie!

پس از چند بار آزمایش و شروع برنامه از ابتدا، نتایج مقایسه در جدول زیر آمده است:

الگوریتم	حداقل زمان	حداکثر زمان
Minimax	4.57 ثانیه	5.34 ثانیه
هرس آلفا بتا	0.16 ثانیه	0.2 ثانیه

نتیجه

هرس آلفا بتا تفاوت عمده ای در ارزیابی درختان بازی بزرگ و پیچیده ایجاد می کند. حتی اگر tic-tac-toe خود یک بازی ساده است، هنوز هم می‌توانیم متوجه شویم که چگونه بدون اکتشافی آلفا-بتا، الگوریتم زمان بیشتری برای توصیه حرکت در نوبت اول می‌گیرد.

(برچسب‌ها به ترجمه)# python

منتشر شده در 1403-01-20 19:55:04

امتیاز شما به این مطلب